Jones M., Fleming S.A. Organic Chemistry

Подождите немного. Документ загружается.

20.3 Electrocyclic Reactions 1039

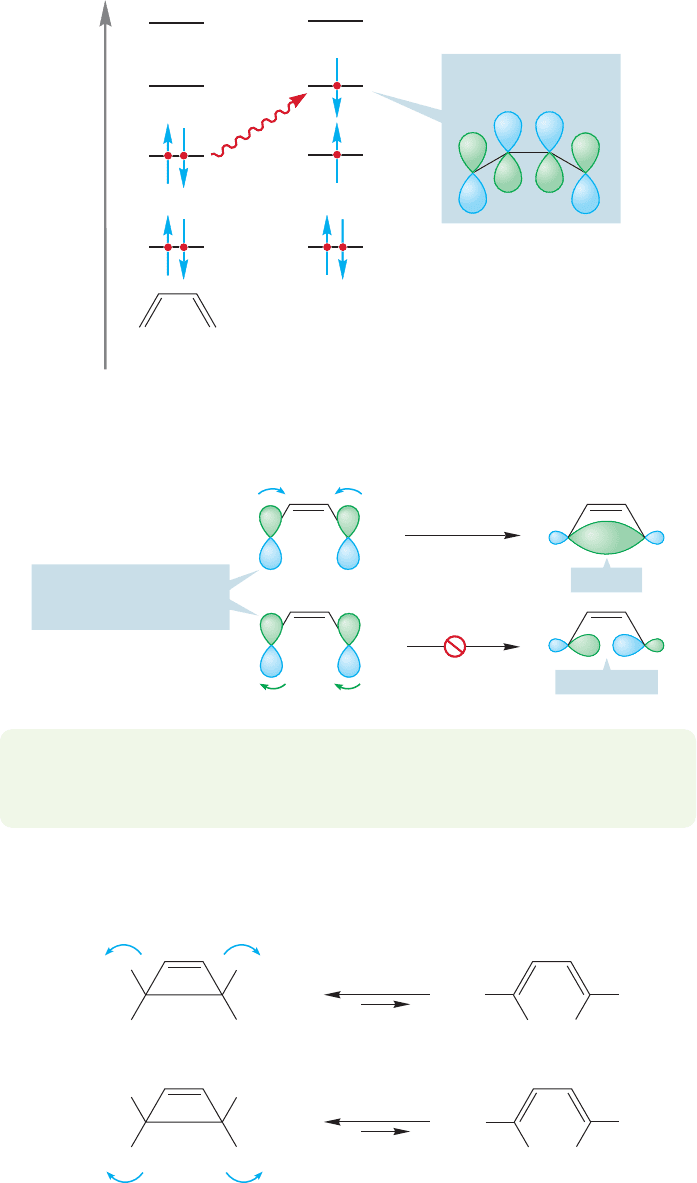
, creating a new, “photochemical HOMO” (Fig. 20.13). No longer does

conrotation in the HOMO, now

, create a bond between the end carbons.£

££

PROBLEM 20.2 Figure 20.14 shows only one disrotatory and one conrotatory

mode. Verify that the other possible disrotation produces a bond between the two

carbons, and that the other possible conrotation produces an antibond.

Energy

HOMO = Φ

hν

HOMO = Φ

New “photochemical

HOMO” is Φ

FIGURE 20.13 The HOMO involved

in the photochemical reaction of

butadiene is .£

Bonding

disrotation

conrotation

End lobes of ⌽

of butadiene, the

“photochemical HOMO”

Antibonding

FIGURE 20.14 The photochemical

HOMO ( ) demands disrotation.

In this molecular orbital, conrotation

produces an antibond.

E = COOCH

COOCH

OOC

cis

cis,cis (Z,Z)

disrotation

COOCH

trans,trans (E,E)

disrotation

OOC

hν

FIGURE 20.15 Disrotation

interconverts the cis disubstituted

cyclobutene and the cis,cis and

trans,trans dienes.

Two disrotatory modes interconvert the cis 3,4-disubstituted cyclobutene and the

cis,cis and trans,trans isomers of the butadiene (Fig. 20.15).

For an orbital of this symmetry, conrotation creates an antibond. In the photochem-

ical reaction, it is disrotation that creates the bonding interaction (Fig. 20.14).

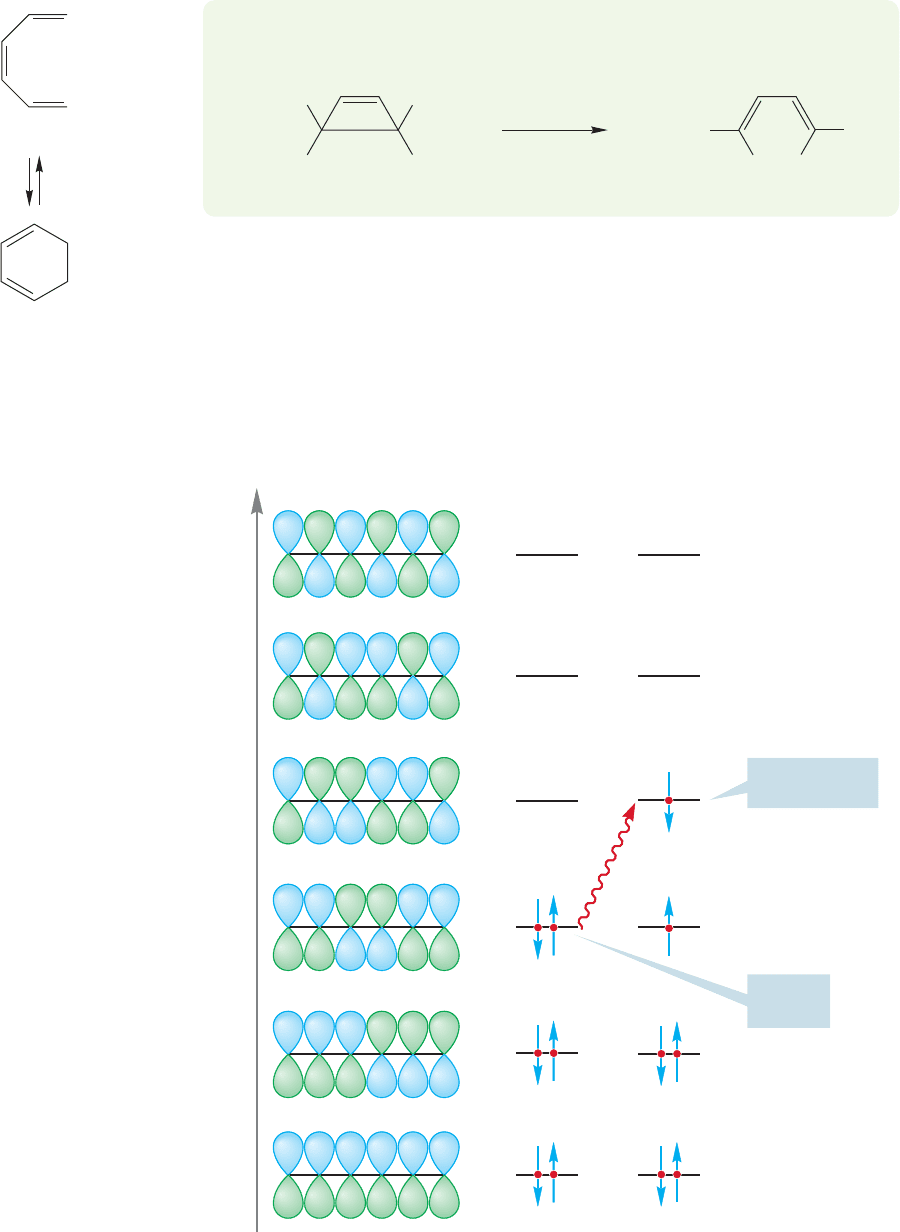
Let’s now use this technique for analyzing electrocyclic reactions to make

some predictions about the 1,3,5-hexatriene–1,3-cyclohexadiene system (Fig.

20.16).

Because it is always easier to look first at the open polyene system, we will con-

sider the π molecular orbitals for hexatriene (Fig. 20.17).The HOMO for the ther-

mal reaction is , and that for the photochemical reaction, .£

1040 CHAPTER 20 Reactions Controlled by Orbital Symmetry

PROBLEM 20.3 Show that disrotation in the photochemical reaction of trans

3,4-disubstituted cyclobutene leads to the cis,trans isomer of the butadiene.

COOCH

OOC

cis,trans (Z,E )

disrotation

hν

cis-1,3,5-Hexatriene

1,3-Cyclohexadiene

FIGURE 20.16 Another electrocyclic

reaction interconverts cis-1,3,5-

hexatriene and 1,3-cyclohexadiene.

Energy

hν

Thermal

HOMO

Photochemical

HOMO

FIGURE 20.17 The π molecular orbitals for 1,3,5-hexatriene.The thermal HOMO is

and the photochemical HOMO is .

20.3 Electrocyclic Reactions 1041

As the open triene closes to the cyclohexadiene (Fig. 20.18),the only way to cre-

ate a bonding interaction between the end carbons is to close in a disrotatory fash-

ion from , and in a conrotatory fashion from . So, we predict that the thermal

interconversion will occur in a disrotatory way, and that the photochemical reaction

must involve conrotation.

To test these predictions we need some labeled molecules. The trans,cis,trans-

2,4,6-octatriene shown in Figure 20.19 will do nicely. A disrotatory thermal closure

to cis-5,6-dimethylcyclohexa-1,3-diene and a conrotatory photochemical closure to

the trans isomer are both known.

disrotation

End lobes of Φ

(the HOMO)

disrotation

Thermal reactions

conrotation

End lobes of

of hexatriene

(photochemical HOMO)

conrotation

Photochemical reactions

hν

FIGURE 20.18 For the hexatriene–cyclohexadiene system, in order to produce a bonding interaction, the thermal

reactions must take place in a disrotatory fashion and the photochemical reactions in a conrotatory way.

hν

disrotation

conrotation

H H

trans,cis,trans

cis

>95% trans

HCH

WEB 3D WEB 3D

FIGURE 20.19 The experimental

results bear out the predictions.

The thermal reaction is disrotatory

and the photochemical reaction is

conrotatory.

Figure 20.19 shows the apparent formation of a single enantiomer of trans-5,6-

dimethylcyclohexa-1,3-diene from an achiral precursor, which cannot be possible.

We have not taken the trouble to draw both enantiomers of the racemic mixture of

the trans-5,6-dimethylcyclohexa-1,3-diene formed in the reaction. This omission

leads directly to Problem 20.4.

CONVENTION ALERT

1042 CHAPTER 20 Reactions Controlled by Orbital Symmetry

The first two rows of Table 20.1 summarize the results so far. They also point

out that the cyclobutene–1,3-butadiene interconversion is a four-electron process,

whereas the hexatriene–1,3-cyclohexadiene reaction involves six electrons. In

the cyclobutene–butadiene reaction, the four electrons in the σ and π orbitals of the

cyclobutene come to occupy the

and

orbitals of 1,3-butadiene. Similarly, the

six electrons in the σ,

, and

of 1,3-cyclohexadiene become the six electrons

, and

of the 1,3,5-hexatriene molecule.£££

££

TABLE 20.1 Rotatory Motions in Electrocyclic Reactions

Number of

Reaction Electrons Thermal Photochemical

Cyclobutene–butadiene 4 (4n) Conrotation Disrotation

Hexatriene–cyclohexadiene 6 (4n  2) Disrotation Conrotation

All 4n electrocyclic reactions 4n Conrotation Disrotation

All 4n  2 electrocyclic reactions 4n  2 Disrotation Conrotation

trans

“Dot” means

“H up”

(a)

PROBLEM 20.4 Figure 20.19 shows only one conrotatory and one disrotatory

mode. Show that the other disrotation and conrotation give the same relative

stereochemical results.

PROBLEM 20.5 Why are cyclohexadienes formed only from the trans,cis,trans

isomer shown in Figure 20.19? Why does the trans,trans,trans triene not give a

similar reaction?

PROBLEM 20.6 Work out the predicted products from the cis,cis,trans and

cis,cis,cis isomers of 2,4,6-octatriene for both photochemical and thermal

reactions.

It turns out that all 4n systems behave like the four-electron case (thermal

reactions conrotatory and photochemical reactions disrotatory) and all 4n  2

systems behave like the six-electron case (thermal reactions disrotatory and pho-

tochemical reactions conrotatory). This generalization is shown in the second

half of Table 20.1, which gives the rules for all electrocyclic reactions. Now, if

you can count the number of electrons correctly you can easily predict the stereo-

chemistry of any electrocyclic reaction without even working out the molecu-

lar orbitals.

PROBLEM 20.7 Provide mechanisms for the following reactions:

(continued)

20.4 Cycloaddition Reactions 1043

(d)

(c)

trans

cis,cis

trans,trans

hν

WEB 3D WEB 3D

(b) Dewar benzene (p. 573) lies perched some 60 kcal/mol higher in energy than

its isomer benzene. It would seem that a simple stretching of the central bond in

Dewar benzene would inevitably and easily give benzene. Yet Dewar benzene

rearranges to benzene only quite slowly. Why?

20.4 Cycloaddition Reactions

Cycloaddition reactions are also orbital symmetry-

controlled, pericyclic reactions. We have seen one

example already, the Diels–Alder reaction, and we will

use it as our prototype. We found the Diels–Alder

cycloaddition to be a thermal process that takes place

in a concerted (one-step) fashion, passing over a cyclic

transition state. Several stereochemical labeling exper-

iments were described in Chapter 12 (p. 549), all of

which showed that the reaction involved neither

diradical nor polar intermediates. This stereospecifici-

ty is important because orbital symmetry considerations

apply only to concerted reactions. Of course, all reac-

tions can be subdivided into series of single-step, sin-

gle-barrier processes, and each of these steps could be

analyzed separately by orbital symmetry. However, it makes no sense to speak of the

overall orbital symmetry control of a multistep process.

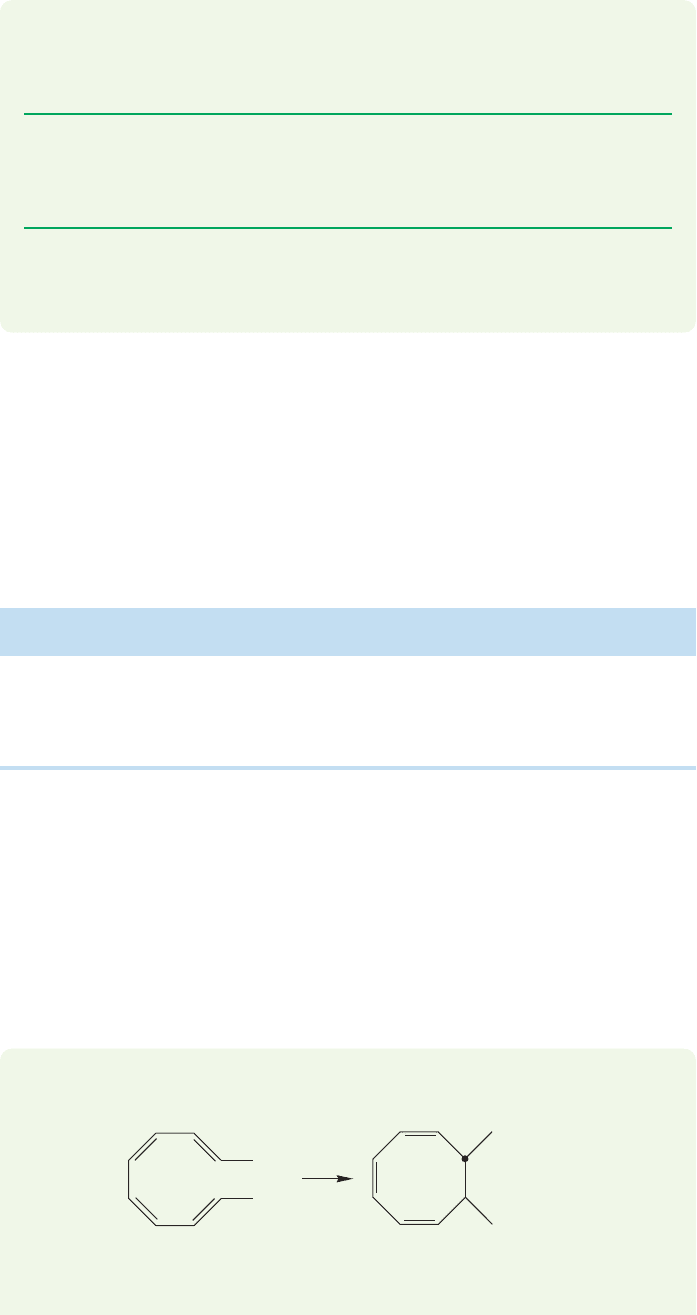
When a diene and dienophile approach each other in the Diels–Alder reaction,

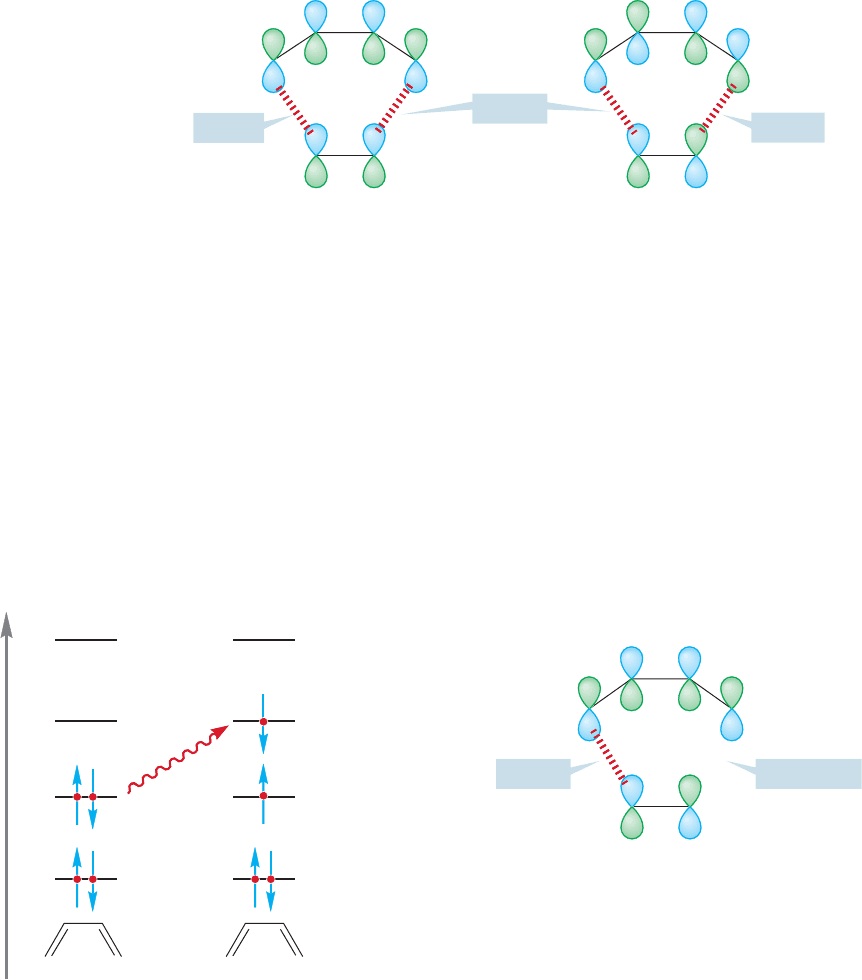
the important orbital interactions are between the HOMOs and LUMOs. As

Figure 20.20 shows, there are two possible HOMO–LUMO interactions,

HOMO

(diene)

–LUMO

(dienophile)

and HOMO

(dienophile)

–LUMO

(diene)

.The stronger of

π∗

LUMO

(dienophile)

HOMO

(dienophile)

LUMO

(diene)

Diene Dienophile

HOMO

(diene)

Energy

FIGURE 20.20 The two possible

HOMO–LUMO interactions in the

prototypal Diels–Alder reaction

between butadiene and ethylene.

1044 CHAPTER 20 Reactions Controlled by Orbital Symmetry

these two will control the reaction. Remember: The strength of orbital overlap, and

the magnitude of the resulting stabilization, depends on the relative energies of the

two orbitals that are mixing.The closer the two are in energy, the stronger the inter-

action. In the simplest Diels–Alder reaction between ethylene and 1,3-butadiene,

the two HOMO–LUMO interactions are of equal magnitude and so we must look at

the orbital symmetry of both HOMO

(diene)

–LUMO

(dienophile)

and HOMO

(dienophile)

–

LUMO

(diene)

.Figure 20.21 shows the symmetry relationships for this reaction. Don’t

forget that in the Diels–Alder and related reactions the two participants approach

each other in parallel planes (p. 548).

π (HOMO) π* (LUMO)

(HOMO)Φ

(LUMO)

HOMO

(dienophile)

–LUMO

(diene)

HOMO

(diene)

–LUMO

(dienophile)

BondingBonding

Bonding

FIGURE 20.21 The orbital overlaps

in the two HOMO–LUMO

interactions of the Diels–Alder

reaction. Either of the HOMO–

LUMO interactions can lead to

product.

Both interactions involve bonding overlaps at the points of formation of the two

new σ bonds.Accordingly, it’s no surprise to find that the thermal Diels–Alder reac-

tion occurs. One says that the reaction is “allowed by orbital symmetry.”

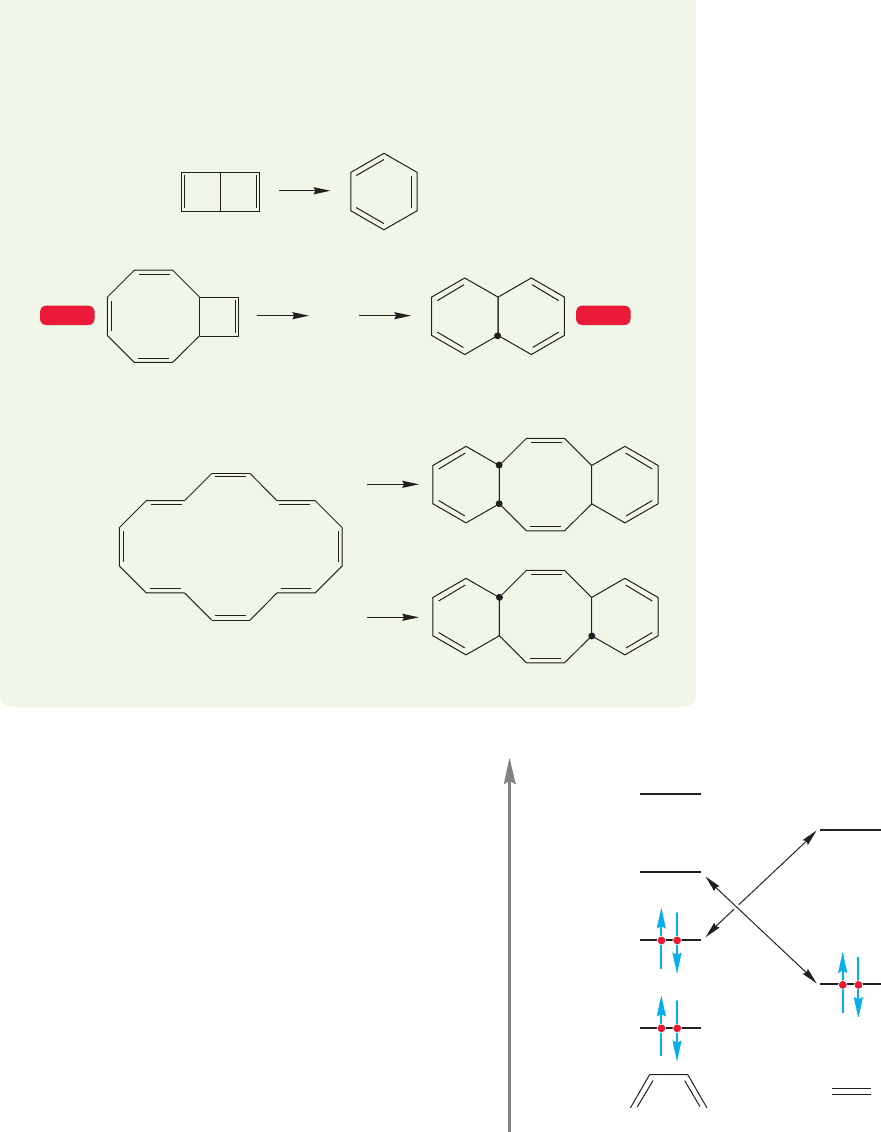
What about the photochemical Diels–Alder reaction? The observation that this

reaction is most uncommon leads us to the immediate suspicion that there is some-

thing wrong with it. Usually, the absorption of a photon will promote an electron

from the HOMO to the LUMO. In this case, the lower energy HOMO–LUMO

gap is that in the diene partner. Absorption of light creates a new photochemical

HOMO for the diene,

, and now the HOMO–LUMO interaction with the

dienophile partner involves one antibonding overlap. Both new bonds cannot be

formed at the same time (Fig. 20.22). So this photochemical Diels–Alder reaction

is said to be “forbidden by orbital symmetry.”

Photochemical

HOMO

Energy

hν

π* (LUMO)

Photochemical

HOMO =

Bonding

Antibonding!

FIGURE 20.22 Absorption of a photon results in the formation of a new HOMO,

.The HOMO

(diene)

–LUMO

(dienophile)

interaction involves one antibond.The photo-Diels–Alder reaction is forbidden by orbital symmetry.

20.4 Cycloaddition Reactions 1045

PROBLEM 20.8 What would happen if the light were used to promote an electron

from the HOMO of the alkene (π) to the LUMO of the alkene (π*)? Would the

Diels–Alder reaction be allowed or forbidden? Show your analysis.

Let’s now analyze another potential cycloaddition, the joining together of a

pair of alkenes to give a cyclobutane (Fig. 20.23). This process can be called

a2  2 reaction because it involves a two-electron π bond combining with

another two-electron π bond (alkene  alkene). Using this same terminology, a

Diels–Alder reaction (diene  dienophile) is a 4  2 reaction. But be careful; using

this terminology makes most sense in describing the electrons involved in the reac-

tion, whereas another common use of 2  2, 4  2, etc., is to describe the number

of atoms involved in a cyclization.

Two alkenes

A cyclobutane

FIGURE 20.23 The hypothetical

combination of two alkenes to give

a cyclobutane.

PROBLEM 20.9 Will the 2  2 reaction between a pair of ethylenes to produce a

cyclobutane be exothermic or endothermic? Explain.

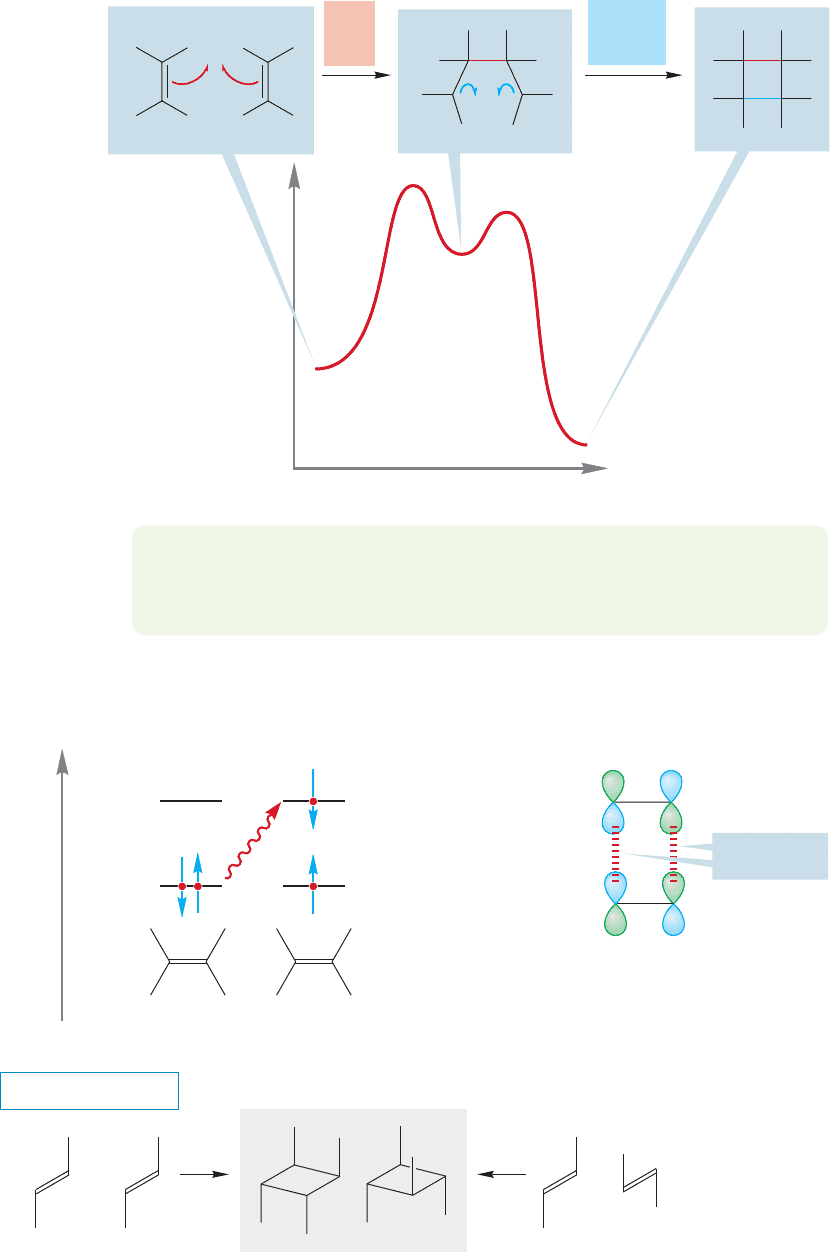
The HOMO and LUMO in an alkene are easy to identify, and it is quickly obvi-

ous that here, too, the apparently easy bond formation shown by the arrow formal-

ism used in Figure 20.23 is thwarted by an antibonding interaction as the two

molecules come together (Fig. 20.24).

π* (LUMO)

(HOMO)

(LUMO)

Bonding

Antibonding

Energy

FIGURE 20.24 An analysis of the

HOMO and LUMO for the reaction

of two alkenes to give a cyclobutane

shows that it is forbidden by orbital

symmetry. There is an antibonding

interaction.

Therefore we might guess that the thermal dimerization of ethylenes would be

a rare process and we would be exactly correct. Moreover, in most of the reactions

1046 CHAPTER 20 Reactions Controlled by Orbital Symmetry

PROBLEM 20.10 Predict the stereochemistry of the product formed in the 2  2

cycloaddition of a pair of cis disubstituted ethylenes, (see

Fig. 20.25).

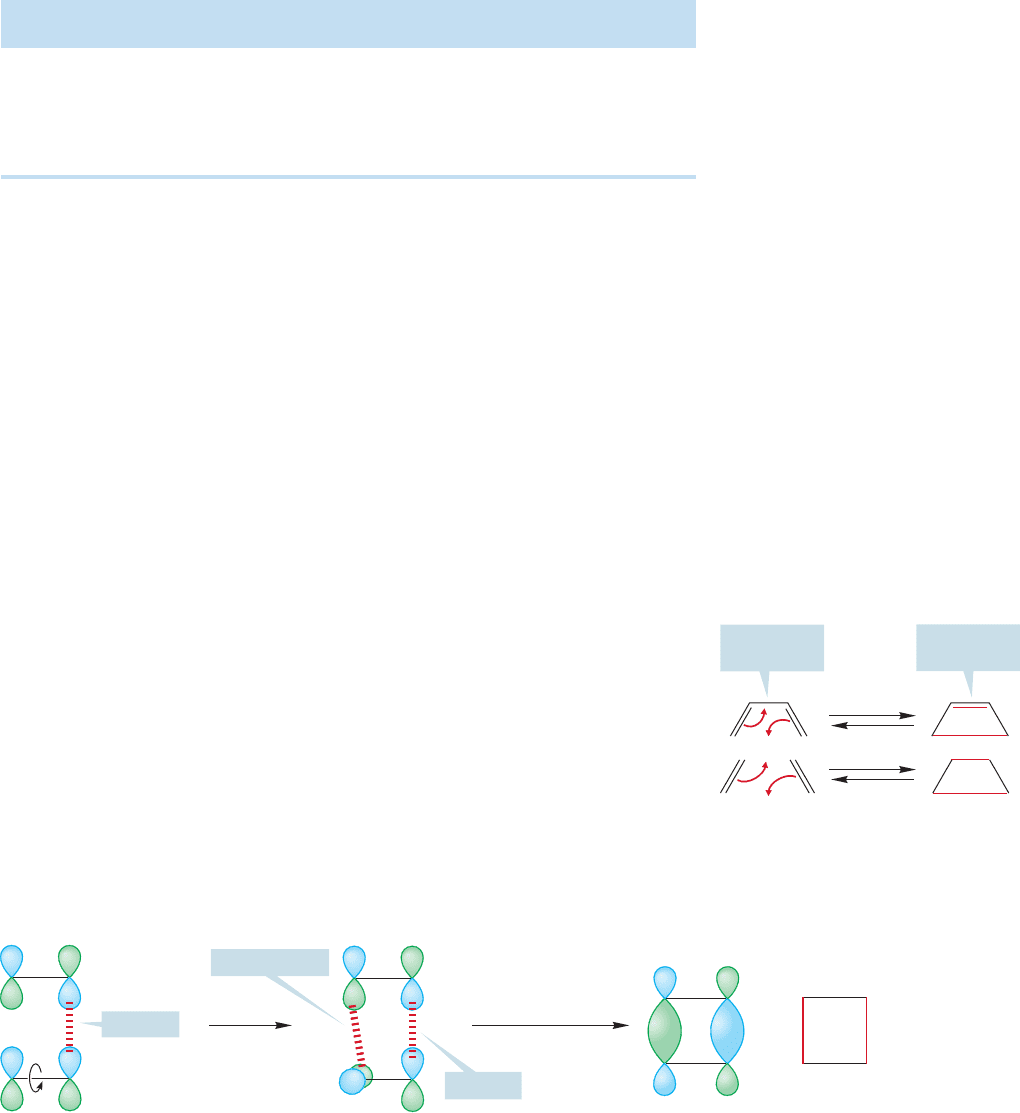
What about the photochemical dimerization of alkenes? Promotion of a single

electron creates a new photochemical HOMO (Fig. 20.26a), and now the symme-

tries are perfect for a HOMO–LUMO interaction involving two bonding

Energy

Reaction progress

form

one

bond

form

the other

bond

. .

R R

R R R

R R

R R R R

R R

FIGURE 20.25 The known

dimerizations of alkenes can

be shown to involve diradical

intermediates.This reaction

is not concerted.

π*

(LUMO)

(photochemical

HOMO)

Photochemical

HOMO

(HOMO)

(LUMO)

Energy

hν

Both bonding

interactions

+++

hν

A REAL EXAMPLE

(a)

(b)

FIGURE 20.26 The photochemical dimerization of two butenes.

of this kind that do occur, it is clear that the two new bonds are formed sequentially

and not in a concerted manner (Fig. 20.25).

20.4 Cycloaddition Reactions 1047

overlaps. In contrast to the thermal reaction, the photochemical dimerization of two

ethylenes is allowed.For example, the photochemical dimerization of trans-2-butene

gives the two cyclobutanes shown in Figure 20.26b.

Again, it’s time for generalization. The first two rows of Table 20.2 show what

we have so far.

TABLE 20.2 Rules for Cycloaddition Reactions

Number of ␲

Reaction Electrons Thermal Photochemical

Alkene  alkene cyclobutane 4 (4n)No Yes

Alkene  diene cyclohexene 6 (4n  2) Yes No

(Diels–Alder)

All 4n reactions 4n No Yes

All 4n  2 reactions 4n  2Yes No

Table 20.2 summarizes all 4n and 4n  2 reactions. Other 4n processes will fol-

low the rules for the 2  2 dimerization of a pair of alkenes, and 4n  2 processes

will resemble the 4  2 cycloaddition we know as the Diels–Alder reaction. Perhaps

you can see the relationship to aromaticity (4n  2) that plays a role in this analysis.

The transition state for these cycloaddition reactions is cyclic and will be allowed only

in the cases where the number of electrons makes the transition state aromatic,

4n  2 electrons for thermal processes and 4n for photochemical reactions.

Now compare Table 20.1 and Table 20.2. This comparison should be a bit dis-

quieting to you. Notice how much more information is available for electrocyclic

reactions than for cycloadditions.For the electrocyclic reactions,we have a clear stereo-

chemical prediction of how things must happen. For example, the 4n processes

undergo conrotatory thermal ring-closing reactions and disrotatory photochemical

ring-closing reactions. On the other hand, for cycloadditions, all we get is a crude

“thermal no,” “photochemical yes” message; a much less detailed picture.

Electrocyclic reactions are not really different from cycloadditions.Figure 20.27 com-

pares the equilibration of 1,3-butadiene and cyclobutene with the 2  2 dimerization

of a pair of ethylenes.The only difference is the extra σ bond in butadiene,and this bond

is surely not one of the important ones in the reaction—it seems to be just going along

for the ride. Why should its presence or absence change the level of detail available to

us through an orbital symmetry analysis? It shouldn’t, and in fact, it doesn’t.

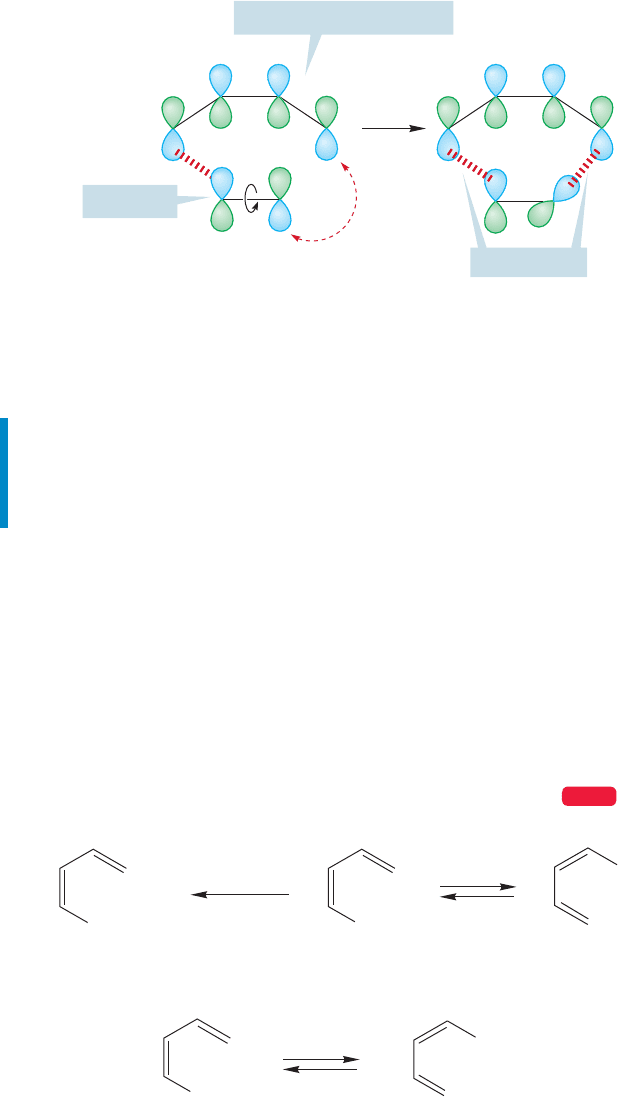
Look again at Figure 20.24, from which we derived the information that the ther-

mal 2  2 dimerization of a pair of ethylenes was forbidden. It’s only forbidden if

we insist on smushing the two ethylenes together head to head exactly as shown in

the figure. If we are more flexible, and allow one ethylene to rotate about its

carbon–carbon σ bond as the reaction takes place, the offending antibonding over-

lap vanishes. What orbital symmetry really says is that for the concerted thermal

dimerization of two alkenes to take place, there must be this rotation (Fig. 20.28).

π*

(HOMO)

(LUMO)

Bonding

“2 + 2” Product

a cyclobutane

Bonding

rotate

continue to rotate

Also bonding!

90⬚

FIGURE 20.28 The thermal 2  2 dimerization is allowed if one end of one ethylene can rotate as the reaction occurs.

σ Bond

(single bond)

σ Bond of

double bond

FIGURE 20.27 The equilibration

of cyclobutene and 1,3-butadiene

and the 2  2 dimerization of a pair

of ethylenes are very closely related

reactions.

1048 CHAPTER 20 Reactions Controlled by Orbital Symmetry

Don’t forget; these rules do not include any consideration of thermodynamics.

The processes allowed with a rotation may well not be very favorable thermodynam-

ically, even though they are permitted electronically.

Summary

Cycloaddition reactions involve the coming together of two (or, rarely,even more)

molecules to make a ring.The easiest analysis involves examining the interactions

of the HOMOs and LUMOs of the two fragments forming the ring compound.

20.5 Sigmatropic Shift Reactions

When one heats (Z)-1,3-pentadiene nothing obvious happens, as the starting ma-

terial is recovered, apparently unchanged. Finally, at very high temperatures, radical

reactions begin as carbon–hydrogen bonds are broken. However, a deuterium-label-

ing experiment reveals that much is happening long before the energies necessary

for the formation of radicals have been reached (Fig. 20.30).

Both bonding

rotate

π* (LUMO)

(photochemical HOMO)

FIGURE 20.29 The photochemical

4  2 reaction (the Diels–Alder

reaction) is also allowed if a rotation

occurs during the cycloaddition or if

the orientation is favorable.

Δ Δ

(high

temperature)

Radicals

Labeling experiment

“No reaction”

(Z)-1,3-Pentadiene

(Z)-5,5,5 -Trideuterio-

1,3-pentadiene

(Z)-1,1,5 -Trideuterio-

1,3-pentadiene

(Z)-1,3 -Pentadiene

(a)

(b)

WEB 3D

FIGURE 20.30 A labeling

experiment reveals the degenerate

thermal rearrangement of

(Z)-1,3-pentadiene.

In practice,this rotation is a very difficult thing to achieve. It is this difficulty that

accounts for the absence of the thermal 2  2 reaction,not the absolute “No”of Table

20.2. Similarly, the photochemical 4  2,Diels–Alder reaction also becomes allowed

if we permit one of the partners to undergo a rotation during the reaction or orient

the two reagents at an angle so that the bonding overlap is possible (Fig. 20.29).