Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

90
в) f ′(х)=0, 2cosx+2cos2x=0; 4cos
2
x+2cosx–2 = 0, 2cos
2
x + cosx – 1 = 0;
D = 1 + 8 = 9; cosx
2
1
4
31
=
+−
,
nx π+
π
±= 2
3
, n ∈ Z;
cosx
1
4
31
−=
−−
, х = π + 2nπ, n ∈ Z,
f(0) = 2sin0 + sin0 = 0, f
⎟
⎠
⎞
⎜
⎝
⎛
π
2
3
= 2sin
2
3π
+ sin3π = –2 + 0 = –2,
2
33
2
3
3
3
2
sin
3
sin2
3
=+=
π
+
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
f ,
f (π) = 2sinπ + sin2π = 0 + 0 = 0,
()() ()()
2
33
3
max;2
2
3
min
2
3
;0
2
3
;0
=
⎟
⎠
⎞
⎜
⎝
⎛
π
=−=
⎟
⎠
⎞
⎜
⎝
⎛
π
=
⎥
⎦
⎤
⎢
⎣
⎡
π
⎥
⎦
⎤
⎢
⎣
⎡
π
fxffxf ;
2) f(x) = 2cosx + sin2x; х∈[0; π]; а) f ′(х) = –2sinx + 2cos2x,
f ′(х) = 0, –2sinx + 2(1 – 2sin
2
x) = 0, 2sin
2
x + sinx –1 = 0, D = 1 + 8 = 9,
()
[] []
[]
⎢
⎢
⎢
⎢
⎣
⎡
π∉
π
−∈π+
π
−=−=
−−
=
π∈
π
π∈
π
∈π+
π
−==
+−
=
;0
2
;,2
2
1
4
31
sin
;0
6
,;0
6
5
;,
6
1
2
1
4
31
sin
Znnxx
Znnxx
n
б) f (0) = 2cos0 + sin0 = 2 + 0 = 2, f (π) = 2cosπ + sinπ = –2 + 0 = –2,
2
33
2
3
3
3
sin
6
cos2
6
=+=
π
+
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
f ,
2
33
2
3
3
3
5
sin
6
5
cos2
6
5
−=−−=
π
+
⎟
⎠
⎞
⎜
⎝
⎛
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
f ,
[]
()()
[]
()()
2
33
6
max;
2
33
6
5
min
;0
;0
=
⎟
⎠
⎞
⎜
⎝
⎛
π
=−=
⎟
⎠
⎞
⎜
⎝
⎛
π
=
π
π
fxffxf .
№ 972
1) v(t) = s′(t) = (6t
2
– t
3
)′ = 12t – 3t
2
2) найдем наибольшее значение v(t)
v′(t) = 12 – 6t ; v′(t) = 0, 12 – 6t = 0, t = 2, t = 2 – точка max.,
v(2) = 24 – 12 = 12.
№ 973
Пусть ВС = х, АС = l – x, тогда
АВ =
=−−
22
)( xxl
xll 2
2
−
,
xllxS
ABC
2
2
1
2
−⋅= .
Найдем наибольшее значение S
ABC
.
91
xll
lxl
xll
lxxll
xll
xl
xllxS
22
3
22
2
22
)2(1
2
2
1
)(
2
2
2
2
2
2
−
−
=
−
−−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−⋅
+−=
′
,
S′(х) = 0,
0
22
3
2
2
=
−
−
xll
lxl
, х =
3
l
, х =
3
l
– точка max.,
АС = l –
3
l
=
3
2l
, АВ =
3
3
99
4
22
lll
=− .
№ 974
Пусть АС = х, тогда СВ = 40 – х.
Тогда площадь найдем по формуле:
() ()
2
2040
2
1
2
1
2
x
xxxCBACxS −=−=⋅=
Исследуем S(х) на max.
S′(х)=20–x; S′ = 0, 20–x=0, x=20, x=20 – точка max. АС = 20,
СВ = 40 – 20 = 20. Это равнобедренный прямоугольный треугольник.
№ 975
Пусть АВ = х = СD и ВС = у = АD, тогда
BD =
α−+ cos2
22
xyyx ,
и АС =
()
απ−+ -cos2
22
xyyx =
=
α++ cos2
22
xyyx
axyyxxyyxBDAC =α+++α−+=+ cos2cos2
2222
−α+++α−+= cos2cos2
22222
xyyxxyyxa
(
)
α−+
22
2
22
cos42 yxyx
a
4
– 4(x
2
+ y
2
)a
2
+ 4(x
2
+ y
2
)
2
= 4(x
2
+ y
2
)
2
– 16x
2
y
2
cos
2
α,
a
4
– 4(x
2
+ y
2
)a
2
+ 16x
2
y
2
cos
2
α = 0, 4(x
2
+ y
2
) = a
2
+ 16
2
222
cos
a
yx α
.
Величина 2(x
2
+ y
2
) зависит от параметра α.
min 4(
x
2
+ y
2
) = a
2
при cos
2
α = 0 α = 90°. Тогда 2(x
2
+ y
2
) =
2
2
a
.
№ 976
Пусть АВ = х, тогда АD = 2
22
xR − ,
42222
22 xxRxxRxABADS −=−=⋅= .
Исследуем
S на max при x∈[0; R].
(
)
422
32
2
422
xxR
xxR
S
−
−
=
′
;
S′ = 0, 0
42
422
32
=
−
−
xxR
xxR
,
92
2
x(R
2
– 2x
2
) = 0;
⎢
⎢
⎣
⎡
±=
=
⇒
⎢
⎢
⎢
⎣
⎡
=
=
2
0
2
0
2
2
R
x
x
R
x
x
,
2
R
−∉[0; R],
x = 0 – точка min., x =
2
R
– точка max.,
R
RR
RAD 2
2
2
2
2
2
2
=⋅=−= ,
2
2
2
RR
R
S =⋅= .
№ 977
Объем пирамиды V =
3
1
h ⋅ S′
осн.
; h = 12 – постоянная, поэтому объем за-
висит только от площади основания. Найдем ее max.
Пусть один катет основания
х, тогда другой
2
16 x− . Тогда площадь
()
422
16
2
1
16
2
1
xxxxxS −=−⋅=
; х ∈ [0; 4]
()
(
)
42
3
42
3
16
8
164
4321
xx
xx
xx
xx
xS
−
−
=
−
−
=
′
;
S′ (х) = 0,
0
16
8
42
3
=
−
−
xx
xx
, x(8 – x
2
) = 0, x = 0, x = 22± , 22−∉ [0; 4],
x = 0 – точка min., x = 22– точка max.,
(
)
4
2
8
64816
2
1
22 ==−⋅=S
,
V =
3
1
⋅ 12 ⋅ 4 = 16.
№ 978
Пусть радиус окружности в основании цилиндра r = х, тогда высота
h =
⎟
⎠
⎞
⎜
⎝
⎛
−
x
R
2
2
. Объем равен
V = h ⋅ S
осн.
= h ⋅ πr
2
. х ∈[0; p],
()
2
4
2
2
32
2
xxp
xx
p
xV
π−π
=⋅π⋅
⎟
⎠
⎞
⎜
⎝
⎛
−= .
Исследуем
V(х) на max. V′(х) =
2
1
(2рπх – 12πх
2
) = рπх – 6πх
2
V′(х) = 0, хπ(р – 6х) = 0,
6
;0
06
0
21
p
xx
xp
x
==⇒
⎢
⎣
⎡
=−
=π
x = 0 – точка min., x =
6
p
– точка max.,
()
216
46
21622
216
4
36
6
3
33
32
p
pp
pp
p
p
V
π
=−
⋅
π
=
π⋅−⋅π
=
⎟
⎠
⎞
⎜
⎝
⎛
.
93
№ 979
k
ABAD
AB
AD
===
25
;
2
5
, AD = 5k, AB = 2k,
DDAABBAAпов
SSABADS
1111
22 ++⋅=
=
= 10k
2
+ 2AA
1
(5k + 2k) = 2S, AA
1
=
k
kS
14
102
2
−
,
(
)
3
2
2
102
7
5
14
102
10 kSk
k
kS
kV −=
−
⋅= .
Исследуем V на max., V′ =
7
5
(2S – 30k
2
); V′ = 0,
7
5
(2S – 30k
2
) = 0,
k=±
15
S
, k=
15
S
– точка max, k=
15
S
;
S
S
AD
3
5
15
5
=
⋅
= , AB=2⋅
15
S
.
№ 980
23
23
2
2
++
+−
=
xx
xx
y
а) Область определения: х
2
+ 3х + 2 ≠ 0; D = 9 – 8 = 1,
1
2
13
−=
+−
≠x
,
2
2
13
−=
−−
≠x
;
б)
()
(
)
(
)
(
)
()
=
++
++−−++−
=
′
2
2
22
23
32232332
xx
xxxxxx
y
()
=
++
−+−−+−−−−++
=
2
2
223223
23
693462693462
xx
xxxxxxxxxx
()
(
)
()
2
2
2
2
2
22
23
26
23
12612
++
−
+=
++
−−
=
xx
x
xx
xx
,
y′ = 0,
(
)
()
0
23
26
2
2
2
=
++
−
xx
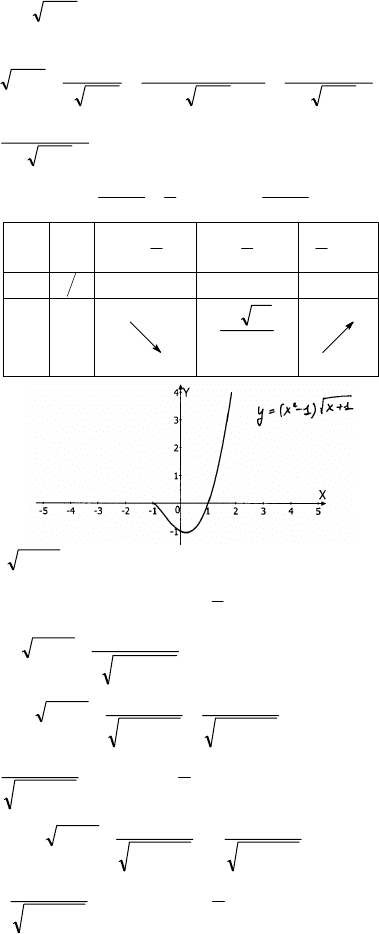
x
, х
2
– 2 = 0, х = 2± ,
x
(–∞;
–2)
–2
(–2;
–
2)
–
2
(–
2;
–1)
–1
(–1;
2)
2
(
2;
+∞)
y′
+
∃
+ 0 –
∃
– 0 +
у
∃
max
∃
min
x = – 2– точка min., x = 2– точка max.
94
№ 981
1)
(
)
11
2
+−= xxy ;
а) Область определения х > 1.
б)
(
)
12
145
12
144
12
1
12
2222
+
−+
=
+
−++
=
+
−
++=
′
x
xx
x
xxx
x
x
xxy ;
в) y′ = 0,
0
12
145
2
=
+
−+
x
xx
, 5х
2
+ 4х – 1 = 0,
D/4 = 4 + 5 = 9; х
1
=
5
1
5
32
=
+−
, х =
1
5
32
−=
−−
x –1
(–1;
5
1
)
5
1
(
5
1
; +∞)
y′
∃
– 0 +
у 0
125
3024
min
2)
3
31|| xxy +⋅= ;
а) D (у) =R; б) у = 0 при х = 0, х =
3
1
−
;
в)
()
()
3
2
3
313
3||
31||
x
x
xxy
+
⋅
++
′
=
′
,
х > 0
() ()
3
2
3
2
3
31
41
31
31
x
x
x
x
xy
+
+
=
+
++=
′
,
y′ = 0,
()
0
31
41
3
2
=
+
+
x
x
, x =
4
1
−
, но х > 0. Не подходит.
х < 0
(
)
()
()
3
2
3
2
3
31
41
31
31
x
x
x
x
xy
+
+
−=
+
−
++−=
′
,
y′ = 0, –
()
0
31
41
3
2
=
+
+
x
x
x =
4
1
−
– точка max.
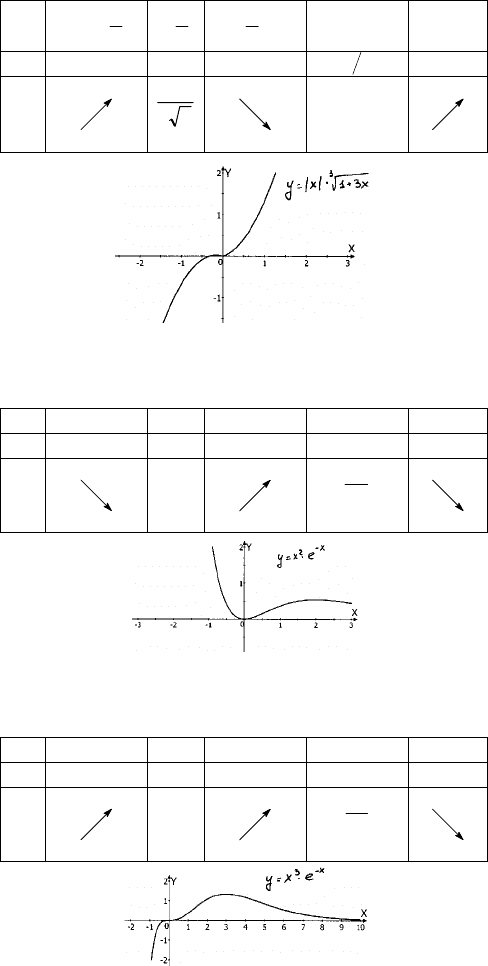
95
x
(–∞;
4
1
−
)
4
1
−
(
4
1
−
; 0)
0
(0; +∞)
y′
+ 0 –
∃
+
у
44
1
max
0
min
3) y = х
2
е
–х
а) Область определения: R
б) у′ = 2хе
–х
– х
2
е
–х
= е
–х
(2х – х
2
)
в) у′ = 0, е
–х
(2х – х
2
) = 0, х = 0; х = 2
x
(–∞; 0)
0 (0; 2) 2
(2; +∞)
y′
– 0 + 0 –
у
0
min
2
4
e
max
4) y = х
3
е
–х
а) D(y) =R
б) у′ = 3х
2
е
–х
– х
3
е
–х
= е
–х
(3х
2
– х
3
)
в) у′ = 0, е
–х
⋅ х
2
(3 – х) = 0, х = 0, х = 3
x
(–∞; 0)
0 (0; 3) 3
(3; +∞)
y′
+ 0 + 0 –
у
0
3
27
e
max
96
№ 982
Запишем II закон Ньютона для груза:
()
α⋅−=α sincos FmgkF
()
α+α
=α
sincos k
mg
F
;
Найдем min F(α):
()
()
()
α+α−⋅
α+α
−
=α
′
cossin
sincos
2
k
k
mg
F
(
)
arctgkktgkkF =α=αα=α=α+α−=α
′
,,sincos,0cossin,0
Ответ:
arctgk=α .

97
X глава.
§ 54 Первообразная
№ 983
1) F′(х) =
6
6
5
x
= х
5
= f(х) ⇒ F(х) является первообр. f(х) на R;
2)
F′(х) =
5
5
4
x
+ 0 = х
4
= f(х) ⇒ F(х) является первообр. f(х) на R.
№ 984
1) F′(х) =
()
()
xf
xx
=−=
−⋅
22
2
12
; 2) F′(х) =
()
xf
xx
==+
2
1
2
1
0;
F(х) является первообр. f(х) при х > 0.
№ 985
1)
5
5
x
- первообр. х
4
, т.к.
4
5
5
x
x
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
, значит, все первообразные имеют
вид F(х) =
5
5
x
+ C;
2) F(х) =
4
4
x
– первообр., т.к. F′(х) =
4
4
3
x
= х
3
= f(х).
Общий вид: F(х) =
4
4
x
+ С.
3) F(х) =
2
2−
−
x
– первообр., т.к. F′(х) =
2
2
3
−
−
−
x
= х
–3
= f(х).
Общий вид: F(х) =
2
2−
−
x
+ С.
4) F(х) =
2
1
2 x⋅ – первообр., т.к. F′(х) =
2
1
2
1
2
1
2
−−
=⋅ xx = f(х).
Общий вид: F(х) =
2
1
2 x⋅ + С.
№ 986
1) Все первообр. функции f(х) = х находятся по формуле:
F(х) =
2
2
x
+ С, т.к. F′(х) = f(х).
Найдем число С, подставив точку (–1; 3):
98
3 =
2
1
+ С, С =
2
5
, F(х) =
2
2
x
+
2
5
;
2) Для функции f(х) =
x
первообр. имеют вид: F(х) =
2
3
3
2
x + С.
Чтобы найти С, подставим точку (9, 10):
10 =
27
3
2
⋅
+ С, С = –8, F(х) =
2
3
3
2
x – 8.
№ 987
1) F′(х) =
()
xfeee
xxx
==⋅=
′
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
333
3
1
33– сущ. при х ∈ R;
2) F′(х) =
() ()
xfxx ==
′
2cos22sin
– сущ. при х ∈ R.
№ 988
1) f(х) = 2х
5
– 3х
2
. По таблице интегрирования:
F(х) =
3
636
33
3
6
2
x
xxx
−=
⋅
−
⋅
.
2) f(х) = 5х
4
+ 2х
3
, тогда F(х) =
24
2
5
5
4
5
45
x
x
xx
+=
⋅
+
⋅
.
3) f(х) =
2
32
x
x
+
, тогда F(х) =
x
x
x
x
3
ln2
1
3
ln2
1
−=
−
⋅
+
−
.
4) f(х) =
x
x
32
3
− , тогда F(х) = x
x
x
x
ln3
1
ln3
2
2
2
2
−−=−
−
⋅
−
.
5) f(х) = 6х
2
– 4х + 3, тогда F(х) =
1
3
2
4
3
6
23
xxx
+− = 2х
3
– 2х
2
+ 3х.
6) f(х) =
xx 64
3
− , тогда F(х) = xxxx
xx
43
2
3
6
3
4
4
3
2
3
3
4
−=
⋅
−
⋅
.
№ 989
1) f(х) = 3cos х – 4sin х, тогда F(х) = 3sin х – 4(–cos х) = 3sin х + 4cos х.
2) f(х) = 5sin х + 2cos х, тогда F(х) = 5 ⋅ (–cos х) + 2 ⋅ sin х = 2sin х – 5cos х.
3) f(х) = е
х
– 2cos x, тогда F(х) = е
х
– 2sin x.
4) f(х) = 3е
х
– sin x, тогда F(х) = 3е
х
– 1 ⋅ (–cos x) = 3е
х
+ cos x.
5) f(х) = 5–е
–x
+3cos x, тогда F(х) = 5x – (–1) е
–x
+ 3sin x = 5x + е
–x
+ 3sin x
6) f(х) = 1 + 3е
x
– 4cos x, тогда F(х) = x + 3е
x
– 4sin x.
7) f(х) =
x
e
x
x 3
2
6
3
+−
, тогда
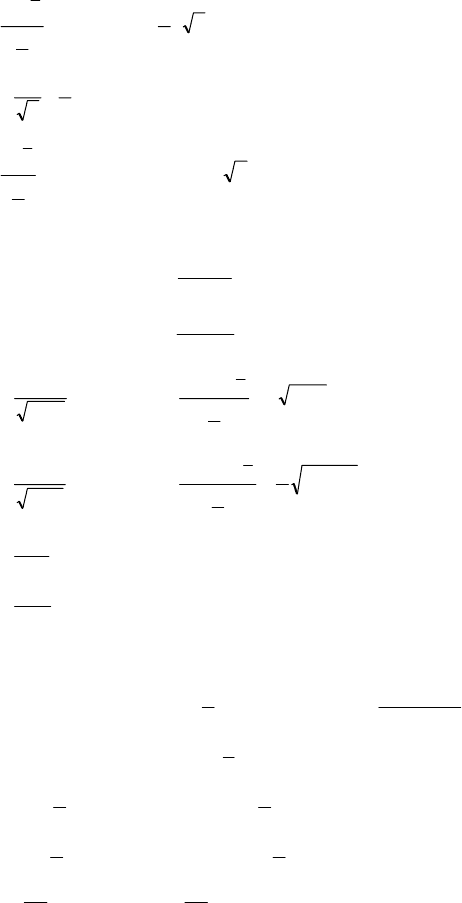
99
F(х) =
3
3
3
4
3ln2
2
9
3ln2
3
4
6
exxxex
x
x
+−=+−
⋅
, x > 0.
8) f(х) =
x
e
x
x
−
−+ 2
34
, тогда
F(х) =
()
xx
exxex
x
−−
++=⋅−⋅−+ 2ln3812ln3
2
1
4
2
1
, x > 0.
№ 990
1) f(х) = (х + 1)
4
, тогда F(х) =
(
)
5
1
5
+x
.
2) f(х) = (х – 2)
3
, тогда F(х) =
(
)
4
2
4
−x
.
3) f(х) =
2
2
−x
, тогда F(х) =
()
24
2
1
22
2
1
−=
−
x
x
, х > 2.
4) f(х) =
3
3
3
+x
, тогда F(х) =
()
()
3
2
3
2
3
2
9
3
2
33
+=
+⋅
x
x
.
5) f(х) =
()
2cos4
1
1
++
−
x
x
, тогда F(х) = ln (x – 1) + 4sin (x + 2), x > 1.
6) f(х) =
()
1sin2
3
3
−−
−
x
x
, тогда
F(х) = 3ln (x – 3) – 2(–cos (x – 1)) = 3ln (x – 3) + 2cos (x – 1), x > 3.
№ 991
1) f(х) = sin (2х + 3), тогда F(х) =
()()
(
)
C
x
Cx +
+
−=++−
2
32cos
32cos
2
1
.
2) f(х) = cos (3х + 4), тогда F(х) =
()
Cx +++ 43sin
3
1
.
3) f(х) = cos (
2
x
– 1), тогда F(х) = 2sin (
2
x
– 1) + C.
4) f(х) = sin (
4
x
+ 5), тогда F(х) = –4 cos (
4
x
+ 5) + C.
5) f(х) =
2
1
+x
e , тогда F(х) = 2
2
1
+x
e + C.
