Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

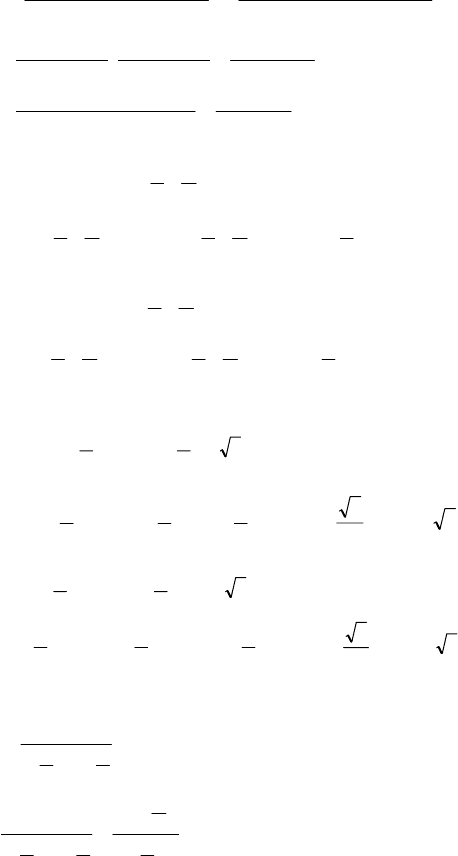
160
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
βα−
β⋅α+β−β+α
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
βα+
βα+β+β−α
=
tgtg
tgtgtgtgtg
tgtg
tgtgtgtgtg
1
:
1
22
(
)
()
=
βα+
β⋅α−
=
β+α
βα−
⋅
βα+
β+α
=
tgtg
tgtg
tgtg
tgtg
tgtg
tgtg
1
1
1
1
1
1
2
2
(
)
()
⇒
β−α
β+α
=
β⋅α+β⋅α
β⋅α−β⋅α
=
cos
cos
sinsincoscos
sinsincoscos
тождество выполняется.
№ 1128
1)
⎟
⎠
⎞
⎜
⎝
⎛
α
−
π
=α+
24
cos2sin1
2
. Преобразуем правую часть:
α+=
⎟
⎠
⎞
⎜
⎝
⎛
α−
π
+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
α
−
π
+=
⎟
⎠
⎞
⎜
⎝
⎛
α
−
π
sin1
2
cos1
24
2cos1
24
cos2
2
,
правая часть равна левой, следовательно, тождество выполняется.
2)
⎟
⎠
⎞
⎜
⎝
⎛
α
−
π
=α−
24
sin2sin1
2
. Преобразуем правую часть:
α−=
⎟
⎠
⎞
⎜
⎝
⎛
α−
π
−=
⎟
⎠
⎞
⎜
⎝
⎛
α
−
π
−=
⎟
⎠
⎞
⎜
⎝
⎛
α
−
π
sin1
2
cos1
24
2cos1
24
sin2
2
,
права часть равна левой, следовательно, тождество выполняется.
№ 1129
1) α=
⎟
⎠
⎞
⎜
⎝
⎛
π
−α−
⎟
⎠
⎞
⎜
⎝
⎛
π
+α cos3
3
sin
3
sin
Преобразуем левую часть:
=α⋅
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
−α−
⎟
⎠
⎞
⎜
⎝
⎛
π
+α cos
3
sin2
3
sin
3
sin
α=α⋅⋅ cos3cos
2
3
2
,
правая часть равна левой, следовательно, тождество выполняется.
2)
α=
⎟
⎠
⎞
⎜
⎝
⎛
α−
π
+
⎟
⎠
⎞
⎜
⎝
⎛
α+
π
cos3
6
cos
6
cos
. Преобразуем левую часть:
=α⋅
π
=
⎟
⎠
⎞
⎜
⎝
⎛
α−
π
+
⎟
⎠
⎞
⎜
⎝
⎛
α+
π
cos
6
cos2
6
cos
6
cos
α=α⋅⋅ cos3cos
2
3
2,
следовательно, тождество выполняется.
№ 1130
1)
α=
+
αα
sin
2
22
ctgtg
. Преобразуем левую часть:
α=
+
α
=
+
ααα
sin
1
2
2
2
222
2
tg
tg
ctgtg
, следовательно, тождество выполняется.
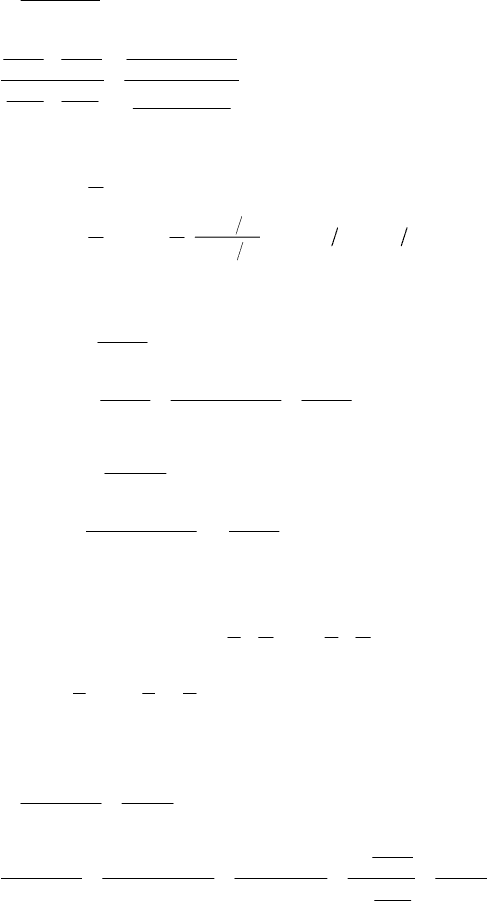
161
2)
α=
α+α
α−α
2cos
tgctg
tgctg
. Преобразуем левую часть, получим:
α=
α⋅α
α−α
=
+
α
α
−
α
α
α⋅α
α+α
α
α
α
α
2cos
cossin
sincos
cos
sin
sin
cos
cossin
2
sin
2
cos
cos
sin
sin
cos
22
.
№ 1131
()
α=
α
α+ sin
2
cos1 tg
. Преобразуем левую часть выражения:
()
(
)
()
()()
α=α⋅α=
α
α
⋅
α
=
α
α+ sin2sin2cos2
2cos
2sin
2
cos2
2
cos1
2
tg , следова-
тельно, тождество выполняется.
№ 1132
1)
α
α
=α−
2
2
cos
2cos
1 tg
. Преобразуем левую часть:
α
α
=
α
α−α
=
α
α
−=α−
22
22
2
2
2
cos
2cos
cos
sincos
cos
sin
11 tg
, следовательно, тождест-
во выполняется;
2)
α
α−
=α−
2
2
sin
2cos
1 ctg
. Преобразуем левую часть:
α
α
−=
α
α−α
=α−
22
22
2
sin
2cos
sin
cossin
1 ctg
, следовательно, тождество выпол-
няется.
№ 1133
=
⎟
⎠
⎞
⎜
⎝
⎛
α
−
π
⋅
⎟
⎠
⎞
⎜
⎝
⎛
α
+
π
α=α+α+
26
cos
26
coscos42coscos1
α+α+=α+α=
⎟
⎠
⎞
⎜
⎝
⎛
π
+αα= 2coscos1coscos2
3
cos
2
1
cos
2
1
cos4
2
,
следовательно, тождество выполняется.
№ 1134
1)
α+
α−
=
α+
α−
tg
tg
1
1
2sin1
sin21
2
. Преобразуем левую часть:
()
α+
α−
=
+
α
α
−
=
α+α
α−α
=
α+α
α−α
=
α+
α−
α
α
tg
tg
1
1
1
cos
sin
1
sincos
sincos
sincos
sincos
2sin1
sin21
cos
sin
2
222
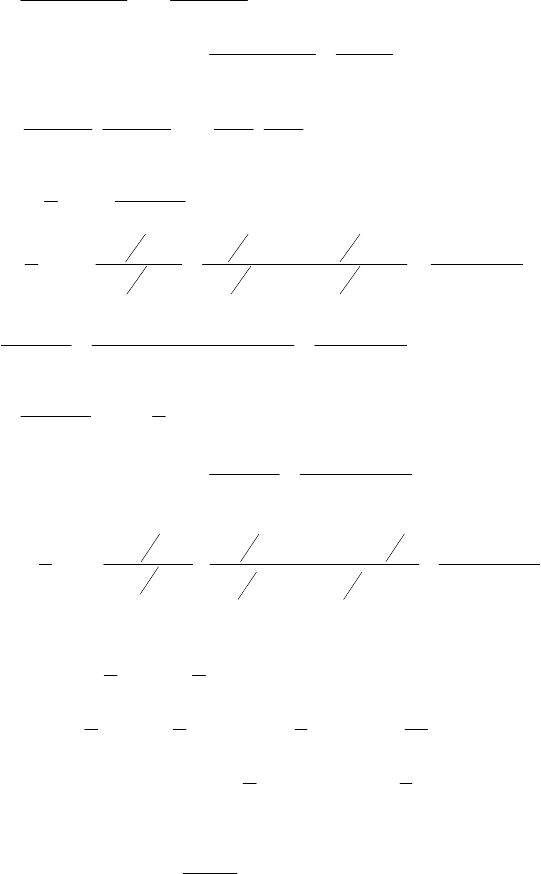
162
2)
(
)
α
α−
+=
αα
2
2
2
22
4
1
1
cossin4
1
tg
tg
.
Преобразуем левую часть:
α+=
α
=
αα
21
2sin
1
cossin4
1
2
222
ctg .
Преобразуем правую часть, получим:
(
)
(
)
α+=
α
⋅
α
+=
α
α−
⋅
α
α−
+ 21
2
1
2
1
1
2
1
2
1
1
2
22
ctg
tgtgtg
tg
tg
tg
, правая часть равна
левой, следовательно, тождество верно.
3)
α
α+
=
⎟
⎠
⎞
⎜
⎝
⎛
α+
π
2cos
2sin1
4
tg . Преобразуем левую часть:
(
)
()
=
α⋅
π
−α⋅
π
α⋅
π
+α⋅
π
=
α+
π
α+
π
=
⎟
⎠
⎞
⎜
⎝
⎛
α+
π
sin
4
sincos
4
cos
sin
4
coscos
4
sin
4
cos
4
sin
4
tg
α−α
α+α
sincos
sincos
.
Преобразуем правую часть:
()
()()
α−α
α+α
=
α+αα−α
α+α
=
α
α+
sincos
sincos
sincossincos
cossin
2cos
2sin1
2
.
Правая часть равна левой, следовательно, тождество выполняется.
4)
⎟
⎠
⎞
⎜
⎝
⎛
α+
π
=
α+
α−
42sin1
2sin1
2
ctg
.
Преобразуем левую часть:
(
)
()
2
2
sincos
sincos
2sin1
2sin1
α+α
α−α
=
α+
α−
.
Преобразим правую часть:
()
()
(
)
()
=
α⋅
π
+α⋅
π
π
⋅α−α⋅
π
=
α+
π
α+
π
=
⎟
⎠
⎞
⎜
⎝
⎛
α+
π
2
2
2
2
2
sin
4
coscos
4
sin
4
sinsincos
4
cos
4
sin
4
cos
4
ctg
(
)
()
2
2
sincos
sincos
α+α
α−α
Правая часть равна левой, следовательно, тождество выполняется.
№ 1135
1) xxxx 3sin
3
sin
3
sinsin4 =
⎟
⎠
⎞
⎜
⎝
⎛
+
π
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
π
⋅ . Преобразуем левую часть:
=
⎟
⎠
⎞
⎜
⎝
⎛
π
−⋅=
⎟
⎠
⎞
⎜
⎝
⎛
+
π
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
π
⋅
3
2
cos2cos
2
1
sin4
3
sin
3
sinsin4 xxxxx
=+⋅=
⎟
⎠
⎞
⎜
⎝
⎛
π
−π⋅−⋅= xxxxxx sin
2
2
2cossin2
3
cossin22cossin2
= 2sin
х ⋅ cos2х + sinх = sinх(2cos2 + 1) = sinх(3cos
2
х - sin
2
х) = sin3х,
следовательно, тождество выполняется;
2)
x
x
xxx
3sin8
24sin
12cos6cos3cos =
Умножим обе части тождества на 8sin3x и докажем равносильное тож-
дество 8cos3x ⋅ sin3x ⋅ cos6x ⋅ cos12x = sin24x (1)
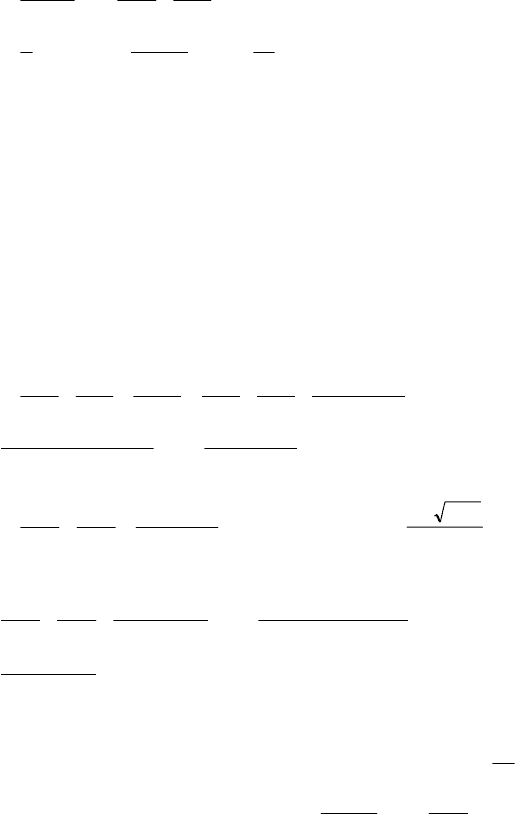
163
Преобразуем левую часть: 8cos3x ⋅ sin3x ⋅ cos6x ⋅ cos12x =
= 4sin6x ⋅ cos6x ⋅ cos12x = 2sin12x ⋅ cos12x = sin24x, следовательно, тож-
дество (1), как и исходное, выполняется.
№ 1136
1)
6
3
4
6
1
12
163 +
−
+
=+
− xxx
, 3х–16+12=3х + 18 – 2х – 6, 2х = 16, х = 8;
2)
()
()
⎟
⎠
⎞
⎜
⎝
⎛
+−=
−
−−−
3
43
7
86
37
3
5
x
x
xx , 35(х–7)–63х–18(х–8)=-21х – 301,
35х – 245 – 63х – 18х + 144 = -21х – 301, -25х = -200, х = 8.
№ 1137
а(х – 3) + 8 = 13(х + 2). Если х = 0, то а(0 – 3) + 8 = 13(0 + 2);
-3а + 8 = 0 + 26, -3а = 18, а = -6.
№ 1138
1 – b(x + 4) = 2(x – 8). Если х = 1, то 1 – b(1 + 4) = 2(1 – 8),
1 – 5b = -14, -5b = -15, b = 3.
№ 1139
1) х(х + 1) – (х + 2)(х + 3) + 9 = х(х + 4) – (х + 5)(х + 2),
х
2
+ х – х
2
– 3х – 2х – 6 + 9 = х
2
+ 4х – х
2
– 2х – 5х – 10, -х = -13, х = 13;
2) 2(х+3)(х+1)+8=(2х+1)(х+5), 2х
2
+2х+6х+6+8=2х
2
+10х+х+5,-3х=-9, х=3.
№ 1140
1)
9
4
3
2
3
3
2
−
=
−
−
+
x
xx
,
()()
0
33
4
3
2
3
3
=
+−
−
−
−
+ xxxx
,
()()
()()
0
33
43233
=
+−
−+−−
xx
xx
,
()()
0
33
13
=
+−
−
xx
x
.
Знаменатель дроби не равен 0, следовательно, х – 13 = 0, т.е. х = 13;
2)
86
11
4
2
2
5
2
++
=
−
+
−
xx
xx
, х
2
– 6х + 8 = 0, 13
1
893
2,1
±=
−±
=x ,
х
1
= 2, х
2
= 4, следовательно х = 2, х = 4 решениями не являются, т.к. об-
ращают в 0 знаменатели дробей.
()()
0
42
11
4
2
2
5
=
−−
−
−
+
− xxxx
,
()()
0
42
1142205
=
−−
−−+−
xx
xx
,
()()
0
42
357
=
−−
−
xx
x
, что равносильно системе,
()()
⎩
⎨
⎧
≠−−
=−
042
0357
xx
x
, х = 5.
№ 1141
1) (a – b)x = a
2
+ (a + b)x, ax – bx = a
2
+ ax + bx, -2bx = a
2
,
b
a
x
2
2
−= ;
2) a
2
x = a + b + b
2
x, x(a
2
– b
2
) = a + b,
22
ba
ba
x
−
+
=
,
ba
x
−
=
1
.

164
№ 1142
1) х
2
– 2х – 15 = 0, 41
1
1511
2,1
±=
+±
=x , х
1
= 5, х
2
= -3;
2) 3х
2
+ 4х – 4 = 0,
3
42
3
1242
2,1
±−
=
+±−
=x ,
3
2
1
=x
, х
2
= -2.
№ 1143
1) (х – 3)(х – 2) = 6(х – 3), (х – 3)(х – 2 – 6) = 0, (х – 3)(х – 8) = 0,
х = 3, х = 8;
2)
0
2
1
6
11
2
=+−
x
x
, 6х
2
– 11х + 3 = 0,
12
711
12
7212111
2,1
±
=
−±
=x ,
3
1
,
2
3
21
== xx
.
№ 1144
1)
0
11
=
−
+
+ x
x
x
x
,
(
)
(
)
0
1
11
2
=
−
++−
x
xxxx
, что равносильно системе:
⎪
⎩
⎪
⎨
⎧
≠−
=++−
01
0
2
22
x
xxxx
, х =0;
2)
13
12
2
13
3
2
+
+
=−
− x
x
x
x
,
(
)
(
)
(
)
(
)
(
)
()()
0
1313
131213132133
2
=
+−
−+−+−−+
xx
xxxxxx
,
()()
0
1313
132621839
2223
=
+−
+−+−+−+
xx
xxxxxx
,
()()
0
1313
3219
23
=
+−
+−−
xx
xxx
, что равносильно системе:
()()
⎩
⎨
⎧
≠+−
=+−−
01313
03219
23
xx
xxx
;
()()
()()
⎩
⎨
⎧
≠+−
=+−−
01313
03733
2
xx
xxx
Решений нет.
№ 1145
1)
x
x
x
xx
x
−
+
−
−
=
+
−
+
−
2
18
4
287
2
7
2
13
2
2
,
2
18
4
287
2
713
2
2
−
−
−
−
=
+
−−
x
x
x
x
x
,
(
)
4
218287
1
83
2
2
−
+−−
=
+
−
x
xx
x
x
,
(
)
(
)
0
4
283
4
3618287
22
2
=
−
−−
−
−
−−−
x
xx
x
xx
,
0
4
1686364187
2
22
=
−
−++−−−
x
xxxxx
, что равносильно системе:
()()
⎩
⎨
⎧
≠+−
=−−
022
08044
2
xx
xx
;
()()
⎩
⎨
⎧
≠+−
=−−
022
020
2
xx
xx
.
165
Решим первое уравнение системы: х
2
– х – 20 = 0,
2
91
2
20411
2,1
±
=
⋅+±
=x , х
1
= 5, х
2
= -4.
2)
x
x
x
x
x
−
−
=
−
−
+
+
3
2
9
12
3
1
2
,
(
)
(
)
(
)
(
)
0
9
321231
2
=
−
+−+−−+
x
xxxx
,
()()
⎩
⎨
⎧
≠+−
=−−++−−+−
033
03621233
22
xx
xxxxxx
,
()()
⎩
⎨
⎧
≠+−
=−−
033
093
xx
x
,
()()
⎩
⎨
⎧
≠+−
−=
033
3
xx
x
.
Ответ: решений нет
№ 1146
1
12
1
1
1
2
32
+
−
=
+
−
+− x
x
x
xx
,
(
)
(
)
0
1
12112
3
2
=
+
+−+−−+
x
xxxx
,
()
()
⎪
⎩
⎪
⎨
⎧
≠+−+
=++−
011
02
2
2
xxx
xx
,
()
()
⎩
⎨
⎧
≠+−+
=−=
011
2 ,1
2
xxx
xx
.
Решением системы является х = 2.
№ 1147
1)
0
1
4 =+−
x
x
.
При х ≠ 0 умножим обе части уравнения на х: х
2
– 4х + 1 = 0,
32
1
142
2,1
±=
−±
=x ;
2)
04
2
10
2
4
2
=+
+
−
+ xx
x
, 0
2
84104
2
=
+
++−
x
xx
,
⎩
⎨
⎧
≠+
=−+
02
0244
2
x
xx
⎩
⎨
⎧
−≠
=−+
2
0122
2
x
xx
, 2х
2
+ 2х – 1 = 0,
2
31
2
211
2,1
±−
=
+±−
=x .
№ 1148
1) х
4
– 11х
2
+ 30 = 0.
Пусть х
2
= у, тогда уравнение примет вид: у
2
– 11у + 30 = 0,
2
111
2
12012111
2,1
±
=
−±
=y , у
1
= 6, у
2
= 5, но у = х
2
, т.е.
х
2
= 6, 6±=x ; х
2
= 5, 5±=x . Ответ: 6 ,5 ±=±= xx .
2) 2х
4
– 5х
2
+ 2 = 0.
Пусть х
2
= у, тогда уравнение примет вид: 2у
2
– 5у + 2 = 0,
4
35
4
16255
2,1
±
=
−±
=y
,
2
1
,2
4
8
21
=== yy , но у = х
2
, т.е.
х
2
= 2, 2±=x и
2
1
,
2
1
2
±== xx . Ответ:
2
1
,2 ±=±= xx .
166
№ 1149
1) 2х
-2
+ 4х
-1
+ 3 = 0.
Пусть х
-1
= у, тогда уравнение примет вид: 2у
2
+ 4у + 3 = 0,
2
642
2,1
−±−
=y ; D < 0, корней нет;
2) (х
2
– х)
2
+ 12 = 8(х
2
– х)
Пусть х
2
– х = у, тогда уравнение примет вид: у
2
+12=8у, у
2
–8у+12 = 0,
24
1
12164
2,1
±=
−±
=y , у
1
= 6, у
2
= 2, но у = х
2
– х, т.е.
х
2
– х – 6 = 0, х
1
= 3, х
2
= -2 и х
2
– х – 2 = 0, х
1
= -1, х
2
= 2.
Ответ: х
1
= 3, х
2/3
= ±2, х
4
= -1.
№ 1150
1)
0
4
2
22
=+−+
a
baxx
,
2
2
2
4
4
2
22
2,1
ba
a
baa
x
±−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+±−
=
.
Ответ:
2
2
2,1
ba
x
±−
=
.
2)
22
2
4
5
22
2
ax
a
ax
x
ax
x
−
=
+
−
−
,
(
)
(
)
0
4
5222
22
2
=
−
−−−+
ax
aaxxaxx
,
0
4
5224
22
222
=
−
−+−+
ax
aaxxaxx
,
0
4
532
22
22
=
−
−+
ax
aaxx
, что равносильно системе:
()()
⎩
⎨
⎧
≠+−
=−+
022
0532
22
axax
aaxx
, 2х
2
+ 3ах – 5а
2
= 0,
4
73
4
4093
22
2,1
aaaaa
x
±−
=
+±−
= , х
1
= а,
ax
2
5
2
−
=
.
№ 1151
ах
2
+bx + c. При а ≠ 0, a > 0, b
2
= 4ac трехчлен ax
2
+ bx + c является
квадратом двучлена.
№ 1152
ax
2
+ bx + a = 0, a ≠ 0,
a
acbb
x
2
4
2
2,1
−±−
= ,
1
4
4
2
4
2
4
2
2222222
21
=
+−
=
−+−
⋅
−−−
=⋅
a
abb
a
abb
a
abb
xx
, следова-
тельно, х
1
, х
2
– взаимно обратные числа.
167
№ 1153
1) |2x – 3| = 7;
а) если 2х – 3 ≥ 0, то 2х – 3 = 7, 2х = 10, х = 5;
б) если 2х – 3 < 0, то 2х – 3 = -7, 2х = -4, х = -2.
2) |x + 6| = 2x;
а) если х + 6 ≥ 0, то х + 6 = 2х, х = 6;
б)если х + 6 < 0, то х + 6 = -2х, х = –2, но тогда х + 6 < 0 не выполняется
Ответ: х = 6.
3) 2х – 7 = |x - 4|;
а) если х – 4 ≥ 0, то 2х–7=х – 4, х = 3, но тогда х – 4
≥ 0 не выполняется;
б) если х – 4 < 0, то 2х – 7 = -х + 4, 3х = 11,
3
2
3
3
11
==x
.
№ 1154
1) |6 – 2x| = 3x + 1;
а) если 6 – 2х ≥ 0, то 6 – 2х = 3х + 1, х = 1;
б) если 6 – 2х < 0, то 2х – 6 = 3х + 1,
х = -7, но тогда 6 – 2х < 0 не выполняется. Ответ: х = 1.
2) 2|x – 2| = |x| - 1
Рассмотрим уравнение на промежутках:
0 2
а) x < 0, тогда 2(2 – х) = -х – 1, 4 – 2х = -х – 1,
х = 5, но x < 0 ⇒ x = 5 не является решением;
б) 0 ≤ х < 2, тогда 2(2 – х) = х – 1, 4 – 2х = х – 1, х =
3
5
;
в) х ≥ 2, 2(х – 2) = х – 1, 2х – 4 = х – 1, х = 3. Ответ: х = 3, х =
3
2
1
.
№ 1155
|x
2
– 3x – 6|=2x.
Найдем корни трехчлена: х
2
– 3х – 6 = 0, D = 9 – 4 ⋅ 1 ⋅ (–6) = 33,
2
333
2,1
±
=
x ,
2
333 −
2
333 +
–
++
1)
⎟
⎟
⎠
⎞
⎢
⎢
⎣
⎡
+∞
+
⎥
⎥
⎦
⎤
⎜
⎜
⎝
⎛
−
∞−∈ ;
2
333
2
333
;
Ux ,
тогда уравнение примет вид: х
2
– 3х – 6 = 2х; х
2
– 5х – 6 = 0,
х
1
= 6, х
2
= -1
⎟
⎟
⎠
⎞
⎢
⎢
⎣
⎡
+∞+
⎥
⎥
⎦
⎤
⎜
⎜
⎝
⎛
−
∞−∈ ;
2
33
3
2
333
;
U ;
168
2)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
∈
2
333
;
2
333
x , -х
2
+3х+6=2х, -х
2
+х+6=0, х
2
–х–6=0, х
1
=3,
х
2
=-2,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
∈−
2
333
;
2
333
2. Наименьший корень х = 3.
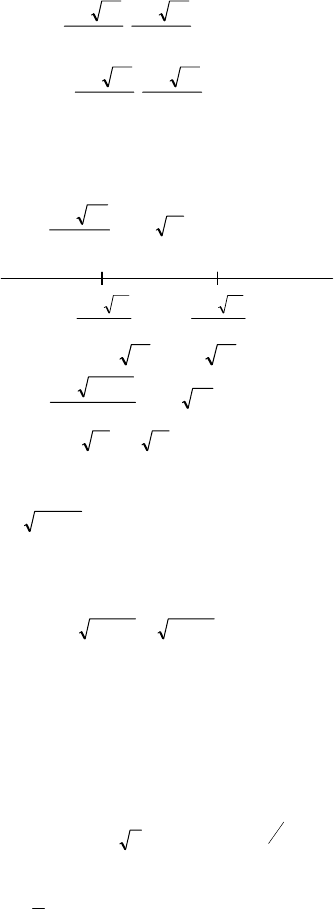
№ 1156
|x
2
– 8x + 5| = 2x
Найдем корни трехчлена: х
2
– 8х + 5 = 0. D = 64 – 4 ⋅ 1 ⋅ 5 = 44
114
12
448
2,1
±=
⋅
±
=
x .
+
+
–
1
114 −
1
114 +
1)
(
]
[
)
+∞+−∞−∈ ;114114; Ux , х
2
– 8х + 5 = 2х, х
2
– 10х + 5 = 0,
Qx ∈±=
−±
= 205
1
5255
2,1
;
2)
(
)
114;114 +−∈x , -х
2
+ 8х – 5 = 2х, -х
2
+ 6х – 5 = 0,
х
2
– 6х + 5 = 0, х
1
= 5, х
2
= 1. Наибольший рациональный корень х = 5.
№ 1157
1)
272 +=+ xx
,
()
;
2
4472
;
02
272
2
2
⎩
⎨
⎧
−≥
++=+
⎩
⎨
⎧
≥+
+=+
x
xxx
x
xx
⎩
⎨
⎧
−≥
−==
⎩
⎨
⎧
−≥
=−+
2
3 ,1
;
2
032
21
2
x
xx
x
xx
.
Ответ: х = 1
2)
522 −−= xx , xx −=− 252
()
;
02
252
2
⎩
⎨
⎧
≥−
−=−
x
xx
;
2
4452
2
⎩
⎨
⎧
≤
+−=−
x
xxx
;
2
096
2
⎩
⎨
⎧
≤
=+−
x
xx
⎢
⎢
⎢
⎢
⎣
⎡
⎩
⎨
⎧
≤
=
⎩
⎨
⎧
≤
=
2
3
2
3
x
x
x
x
.
Ответ: корней нет.
№ 1158
1) 3
х-7
= 81, 3
х-7
= 3
4
, х – 7 = 4, х = 11;
2)
22
5,65
2
=
+− xx
,
2
1
5,65
22
2
=
+− xx
, х
2
– 5х + 6,5 = 0,5,
х
2
– 5х + 6 = 0, х
1
+ х
2
= 5, х
1
⋅ х
2
= 6, х
1
= 2, х
2
= 3;
3)
62
24
4
1
+
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
x
x
x
,
(
)
621
244
+−
=⋅
x
x
x
,
(
)
31
44
+−
=
x
x
x
,
3
44
2
+−
=
xxx
, х
2
– х = х + 3, х
2
– 2х – 3 = 0, х
1
= -1, х
2
= 3.
169
№ 1159
1) 899
155
=−
−xx
,
(
)
8919
15
=−
−x
, 8
9
8
9
5
=⋅
x
, 9
5х
= 9, 5х = 1, х = 1/5;
2) 2
х+4
– 2
х
= 120, 2
х
(16 – 1) = 120, 2
х
= 8, х = 3.
№ 1160
1) 5
2х+5
⋅ 7
3х+1
= 35
1/2(5х+6)
, 5
2х+5
⋅ 7
3х+1
= 5
2,5х+3
⋅ 7
2,5х+3
,
1
75
75
1352
35,235,2
=
⋅
⋅
++
++
xx
xx
, 5
0,5х-2
⋅ 7
-0,5х+2
= 1, 1497
25
5
5,0
5,0
=⋅⋅
− x
x
,
49
25
7
5
5,0
5,0
=
x
x
,
25,0
7
5
7
5
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
x
, 0,5х = 2, х = 4;
2)
6
22
5
1
52,0
2
⎟
⎠
⎞
⎜
⎝
⎛
=⋅
+xx
,
622
555
2
−+−
=⋅
xx
,
622
55
2
−++−
=
xx
,
-х
2
+ 2х + 2 = -6, -х
2
+ 2х + 8 = 0, х
2
– 2х – 8 = 0, х
1
= 4, х
2
= -2.
№ 1161
1) 2,4
3-2х
= 2,4
3х-2
, 3 – 2х = 3х – 2, 5 = 5х, х = 1;
2)
(
) ()
2
5
3
3
5
−
=
xx
, х = -х + 2, 2х = 2, х = 1;
3)
x−
⎟
⎠
⎞
⎜
⎝
⎛
=
16
1
8
1
,
x4
2
1
2
1
8
1
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
,
x4
2
3
2
1
2
1
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
,
x4
2
3
−= ,
8
3
−=x
.
№ 1162
1)
3
2
8
27
9
4
1
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−xx
,
3
2
2
3
3
2
1
3
3
2
2
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−xx
,
3
2
3
2
3
2
332
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
− xx
,
2х + 3 – 3х = 1, -х = -2, х = 2;
2)
21632
3
3
=⋅
xx
, 2
х/3
⋅ 3
х/3
= 6
3
, (6)
х/3
= 6
3
, х/3 = 3, х = 9.
№ 1163
1) 5
х+1
+ 5
х
+ 5
х-1
= 155, 5
х
(5 + 1 + 5
-1
) = 155,
155
5
1525
5 =
⎟
⎠
⎞
⎜
⎝
⎛
++
x
,
5
х
= 25, 5
х
= 5
2
, х = 2;
2) 3
2х
– 2 ⋅ 3
2х-1
– 2 ⋅ 3
2х-2
= 1, 3
2х
(1 – 2 ⋅ 3
-1
– 2 ⋅ 3
-2
) = 1,
1
9
2323
3
2
2
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−⋅−
x
, 3
2х
= 9, 3
2х
= 3
2
, х = 1.
3) 7
х
– 7
х-1
= 6, 7
х
(1 – 7
-1
) = 6, 7
х
= 7, х = 1;
4) 3
х+2
+ 3
х
= 10, 3
х
(3
2
+ 1) = 10, 3
х
= 1, х = 0.
