Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

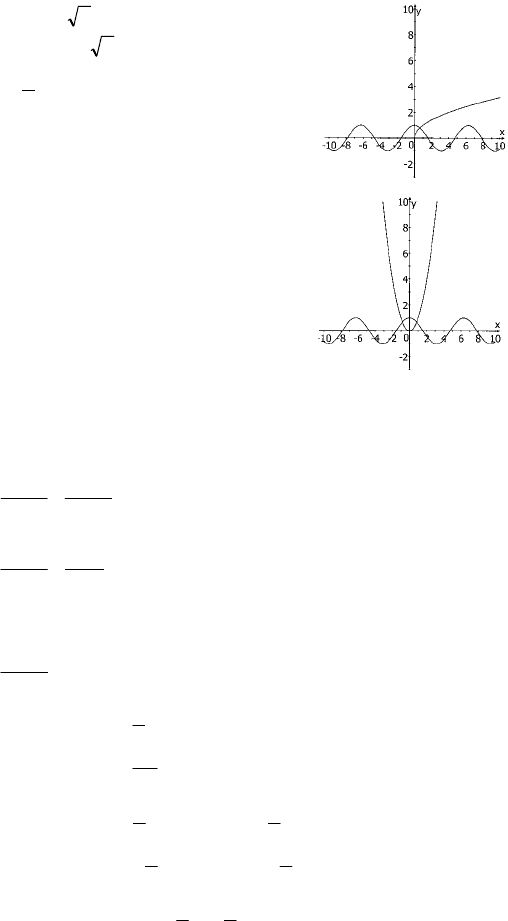
190
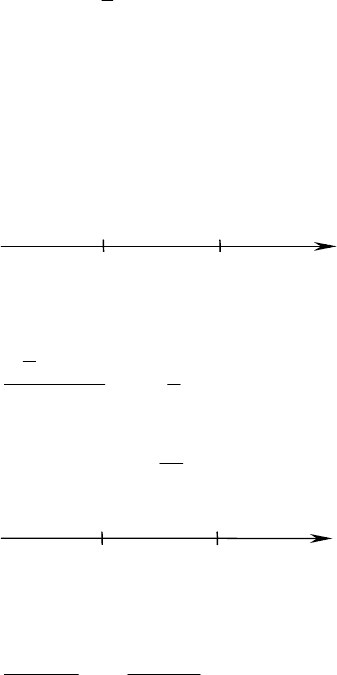
3)
xxcos =
y = cosx,
xy =
2
1
≈x
4) cosx = x
2
y = cosx, y = x
2
8,0±≈x
№ 1202
1) x + 8 > 4 – 3x, 4x > -4, x > -1;
2) 3x + 1 – 2(3 + x) < 4x + 1, 3x + 1 – 6 – 2x – 4x – 1 < 0, -3x < 6, x > -2.
№ 1203
1) 2
12
25
8
34
<
−
−
− xx
, 3(4–3х)–2(5–2х)–2⋅24<0, 12–9x–10+4x–48 < 0,
-5x – 46 < 0, x > -46/5;
2)
2
7
2
6
75
≥
+
−
− xx
б 7(5x – 7) – 6(x + 2) – 42 ⋅ 2 ≥ 0,
35x – 49 – 6x – 12 – 84 ≥ 0, 29x ≥ 145, x ≥ 5.
№ 1204
1)
0
57
45
>
+
−
x
x
а)
⎩
⎨
⎧
>+
>−
057
045
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−
>
>
7
5
5
4
x
x
x > 4/5
б)
⎩
⎨
⎧
<+
<−
057
045
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−<
<
7
5
5
4
x
x
x < -5/7
⎢
⎢
⎢
⎢
⎣
⎡
−<
>
7
5
5
4
x
x
Ответ:
⎟
⎠
⎞
⎜
⎝
⎛
+∞
⎟
⎠
⎞
⎜
⎝
⎛
−∞−∈ ;
5
4
7
5
;
Ux ;
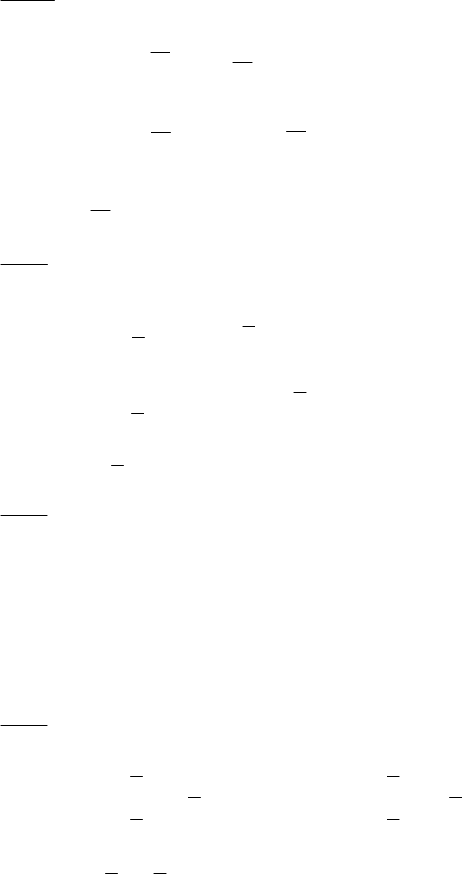
191
2)
0
40
103
>
−
+
x
x
а)
⎩
⎨
⎧
>−
>+
040
0103
x
x
⎪
⎩
⎪
⎨
⎧
<
−>
40
3
10
x
x
⎟
⎠
⎞
⎜
⎝
⎛
−∈ 40;
3
10
x
б)
⎩
⎨
⎧
<−
<+
040
0103
x
x
⎪
⎩
⎪
⎨
⎧
>
−<
40
3
10
x
x
х ∈
φ
⎢
⎢
⎢
⎣
⎡
φ∈
⎟
⎠
⎞
⎜
⎝
⎛
−∈
x
x 40;
3
10
.
Ответ:
⎟
⎠
⎞
⎜
⎝
⎛
−∈ 40;
3
10
x .
3)
0
45
2
>
−
+
x
x
а)
⎩
⎨
⎧
>−
>+
045
02
x
x
⎪
⎩
⎪
⎨
⎧
<
−>
4
5
2
x
x
4
5
2 <<− x
б)
⎩
⎨
⎧
<−
<+
045
02
x
x
⎪
⎩
⎪
⎨
⎧
>
−<
4
5
2
x
x
х ∈
φ
⎢
⎢
⎣
⎡
φ∈
<<−
x
x
4
5
2
Ответ:
4
5
2 <<− x .
4)
0
36
8
>
+
−
x
x
а)
⎩
⎨
⎧
>+
>−
036
08
x
x
⎩
⎨
⎧
−>
<
2
8
x
x
-2 < x < 8
б)
⎩
⎨
⎧
<+
<−
036
08
x
x
⎩
⎨
⎧
−<
>
2
8
x
x
х ∈
φ
Ответ: -2 < x < 8.
№ 1205
1)
0
23
23
<
−
−
x
x
а)
⎩
⎨
⎧
<−
<−
023
023
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
>
3
2
2
3
x
x
;
2
3
>x
; б)
⎩
⎨
⎧
>−
>−
023
023
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<
<
3
2
2
3
x
x
;
3
2
<x
Ответ:
⎟
⎠
⎞
⎜
⎝
⎛
+∞
⎟
⎠
⎞
⎜
⎝
⎛
∞−∈ ;
2
3
3
2
;
Ux .
192
2)
0
29
410
<
+
−
x
x
; а)
⎩
⎨
⎧
<+
<−
029
0410
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−>
>
9
2
2
5
x
x
;
2
5
>x
б)
⎩
⎨
⎧
>+
>−
029
0410
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−<
<
9
2
2
5
x
x
;
9
2
−<x
⎢
⎢
⎢
⎢
⎣
⎡
−<
>
9
2
2
5
x
x
Ответ:
⎟
⎠
⎞
⎜
⎝
⎛
+∞
⎟
⎠
⎞
⎜
⎝
⎛
−∞−∈ ;
2
5
9
2
; Ux .
3)
0
14
718
2
<
−−
−
x
x
; 0
14
718
2
>
+
−
x
x
18 – 7x > 0;
7
18
<x
(4x
2
+ 1 > 0 при любых значениях х). Ответ:
7
18
<x
.
№ 1206
1)
4
3
45
<
−
+
x
x
;
(
)
0
3
3445
<
−
−−+
x
xx
;
0
3
16
<
−
+
x
x
;
⎩
⎨
⎧
<−
>+
03
016
x
x
или
⎩
⎨
⎧
>−
<+
03
016
x
x
;
⎩
⎨
⎧
<
−>
3
16
x
x
или
⎩
⎨
⎧
>
−<
3
16
x
x
; -16 < x < 3;
2)
1
4
2
<
−x
;
()
0
4
412
<
−
−−
x
x
;
0
4
6
<
−
−
x
x
;
⎩
⎨
⎧
>−
<−
04
06
x
x
или
⎩
⎨
⎧
<−
>−
04
06
x
x
;
⎩
⎨
⎧
>
>
4
6
x
x
или
⎩
⎨
⎧
<
<
4
6
x
x
x > 6 или x < 4;
3)
4
3
2
≤
+x
,
(
)
0
3
342
≤
+
+−
x
x
, 0
3
104
≤
+
−
−
x
x
,
⎩
⎨
⎧
>+
≤−−
03
0104
x
x
или
⎩
⎨
⎧
<+
≥−−
03
0104
x
x
;
⎩
⎨
⎧
−>
−≥
3
5,2
x
x
или
⎩
⎨
⎧
−<
−≤
3
5,2
x
x
x ≥ -2,5 или x < -3.
№ 1207
1) 8х
2
– 2х – 1 < 0,
0
2
1
4
1
<
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+ xx
,
2
1
4
1
<<− x
+ +
–
4
1
−
2
1
2) 5x
2
+ 7x ≤ 0,
0
5
7
≤≤− x
.
+ +
–
5
7
−
0
193
№ 1208
1) 0
4
9
2
2
<
−
−
x
x
равносильно
(
)
(
)
()()
⎪
⎩
⎪
⎨
⎧
±≠
<
+−
+−
2
0
22
33
x
xx
xx
,
(
)
(
)
()()
0
22
33
<
+−
+−
xx
xx
–
–
++ +
-3 -2 2 3
()()
3;22;3 U−−∈x ;
2) (2х
2
+ 3)(х + 4)
3
> 0, 2x
2
+ 3 > 0 при любых х;
(x + 4)
3
> 0 равносильно x + 4 > 0; x > -4.
№ 1209
1) 0
145
153
2
≥
−+
−
xx
x
,
()
(
)
⎪
⎩
⎪
⎨
⎧
≠−+
≥−+−
0145
0145153
2
2
xx
xxx
,
(3х – 15)(х – 2)(х + 7) ≥ 0, (х – 5)(х – 2)(х + 7) ≥ 0,
–
–
+
+
-7 2 5
()
[
)
+∞−∈ ;52;7 Ux ;
2)
0
24
1
2
<
++
−
x
x
x
,
()
(
)
⎪
⎩
⎪
⎨
⎧
≠++
<++−
024
0241
2
2
xx
xxx
,
(х – 1)(х
2
+ 4х + 2) < 0,
(
)
(
)
(
)
(
)
022221 <−++−− xxx ,
–
–
+
+
22 −−
1
22 +−
(
)
(
)
1;2222; +−−−∞−∈ Ux
3)
0
32
82
2
2
>
−−
−+
x
x
xx
равносильно
(
)
(
)
⎪
⎩
⎪
⎨
⎧
≠−−
>−−−+
032
03282
2
22
xx
xxxx
(x – 2)(x + 4)(x + 1)(x –3) > 0
+
+
+
–
–
-4 -1 2 3
()()
(
)
+
∞−−−∞∈ ;32;14; UUx .
№ 1210
lg(x
2
+ 8x + 15). Выражение не имеет смысла при x
2
+ 8x + 15 ≤ 0,
x
2
+ 8x + 15 ≤ 0, (x + 3)(x + 5) ≤ 0
+ +
–
-5 -3
x ∈ [-5; -3].
Ответ: -5 ≤ х ≤ -3.
194
№ 1211
(m – 1)x2 – 2(m + 1)x + m – 3 = 0.
Т.к. квадратное уравнение имеет два действительных корня, когда
D>0 и а≠0, то
()()()
⎩
⎨
⎧
≠−
>−−−+
01
0311
2
m
mmm
⎩
⎨
⎧
≠
>−+−++
1
03412
22
m
mmmm
⎩
⎨
⎧
≠
>−
0
026
m
m
3
1
>m
, следовательно, m =2 – наименьшее целое число, при
котором уравнение имеет 2 действительных корня.
№ 1212
(m – 7)x
2
+ 2(m – 7)x + 3 = 0, D < 0, a ≠ 0
()()
⎩
⎨
⎧
≠−
<−−−
07
0737
2
m
mm
⎩
⎨
⎧
≠
<+−+−
7
02134914
2
m
mmm
⎩
⎨
⎧
≠
<+−
7
07017
2
m
m
(
)
(
)
⎩
⎨
⎧
≠
<−−
7
0107
m
mm
(m – 7)(m – 10) < 0
+
+
–
7 10
m ∈ (7; 10).
Ответ: при m = 8, m = 9.
№ 1213
0
149
3
2
1
2
2
<
+−
+
x
x
x
,
()
01493
2
1
22
<+−
⎟
⎠
⎞
⎜
⎝
⎛
+ xxx
.
Выражение принимает отрицательное значение, когда
x
2
– 9x + 14 < 0, т.к. 03
2
2
>+
x
при любых х
х
2
– 9х + 14 < 0, (x – 7)(x – 2) < 0
+
+
–
2 7
x ∈ (2; 7), следовательно, наибольшее целое х = 6.
Ответ: х = 6
№ 1214
0
7
6
2
2
>
−−
−−
x
xx
,
0
7
6
2
2
<
+
−−
x
xx
, x
2
+ 7 > 0 при любых х, а
х
2
– х – 6 < 0 при х ∈ (-2; 3), следовательно, наименьшее целое, х = -1.
№ 1215
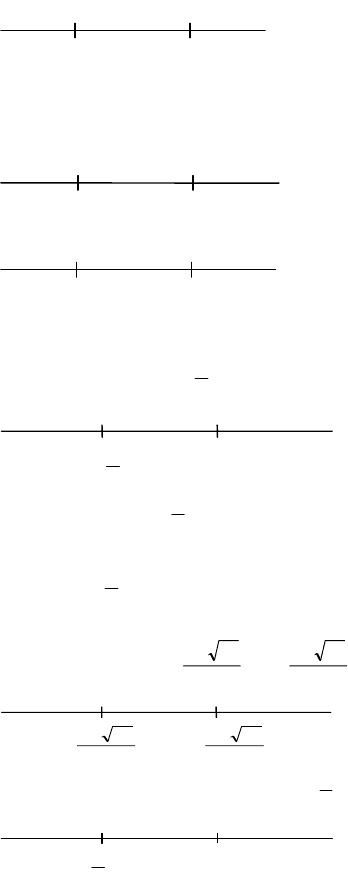
1) |2x – 3| < x, 2x – 3 < x или 3 – 2x < x, 2x – x < 3, x < 3 или –2x –x < -3,
-3x < -3; x > 1. Ответ: 1 < x < 3
2) |4 – x| > x, 4 – x > x или x – 4> x; x < –2 или x ∈
φ
. Ответ: x < –2.
195
3) |x
2
– 7x + 12| ≤ 6, x
2
– 7x + 12 ≤ 6 или –x
2
+ 7x – 12 ≤ 6;
а) x
2
– 7x + 6 ≤ 0, x
1
= 6 и х
2
= 1, 1 ≤ x ≤ 6;
+
+
–
1 6
б) х
2
– 7х + 18 ≥ 0, х
2
– 7х + 18 = 0, D < 0, следовательно, неравенство
справедливо при всех х. Ответ: 1 ≤ х ≤ 6.
4) |x
2
– 3x – 4| > 6, x
2
– 3x – 4 > 6 или –x
2
+ 3x + 4 > 6;
а) х
2
– 3х – 10 > 0, x
1
= 5 и x
2
= -2, x < -2, x > 5;
+
+
–
-2 5
б) -x
2
+ 3x – 2 > 0, x
2
– 3x + 2 > 0, x
1
= 2 и х
2
= 1, 1 < x < 2;
+
+
–
1 2
Ответ: x < -2, 1 < x < 2, x > 5;
5) |2x
2
– x – 1| ≥ 5, 2x
2
– x – 1 ≥ 5 или -2х
2
+ х + 1 ≥ 5
а) 2х
2
– х – 6 ≥ 0,
2
3
1
−=x и х
2
= 2.
+
+
–
2
3
−
2
Следовательно,
2
3
x −≤
, х ≥ 2.
б) -2х
2
+ х – 4 ≥ 0, 2х
2
– х + 4 ≤ 0, D < 0 – корней нет.
Ответ:
2
3
−≤x , х ≥ 2
6) |3x
2
– x – 4| < 2, 3x
2
– x – 4 < 2 или –3x
2
+ x + 4 < 2,
а) 3х
2
– х – 6 < 0 ,
6
731
x,
6
731
x
1
+
=
−
=
;
+
+
–
6
731
−
6
731
+
б) -3х
2
+ х + 2 < 0, 3x
2
– x – 2 > 0,
3
2
1
−=x
, x
2
= 1,
+
+
–
3
2
−
1
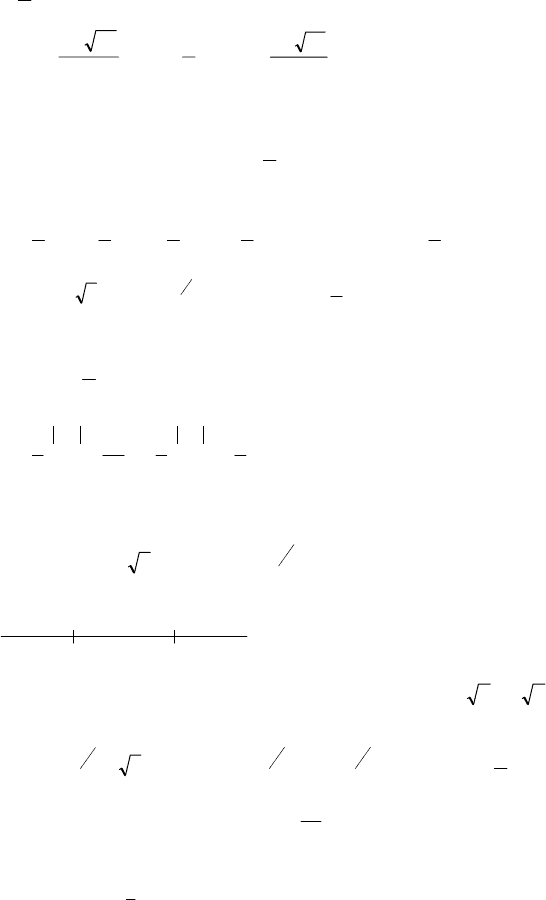
196
x
3
2
<−
, x > 1, но |3x
2
– x – 4| = -3x
2
+ x + 4 при –1 < x < 4/3
Ответ:
3
2
x
6
731
−<<
−
,
6
731
x1
+
<< .
(Опечатка в ответе задачника)
№ 1216
1) 2,5
1-x
> 2,5
-3x
, 1 – x > -3x,
2
1
−>x ;
2) 0,13
x-4
≥ 0,15
2-x
, x – 4 ≤ 2 – x, 2x ≤ 6, x ≤ 3;
3)
12
4
3
3
4
−
⎟
⎠
⎞
⎜
⎝
⎛
≤
⎟
⎠
⎞
⎜
⎝
⎛
xx
,
12
4
3
4
3
−−
⎟
⎠
⎞
⎜
⎝
⎛
≤
⎟
⎠
⎞
⎜
⎝
⎛
xx
, -2x ≥ x – 1,
3
1
≤x ;
4)
33
4
>
− x
,
2
1
4
33 >
− x
, -4x > ½,
8
1
−<
x .
№ 1217
1)
4
1
2
5
<
+−x
, 2
-х+5
< 2
-2
, -x + 5 < -2, x > 7;
2)
27
1
3
1
2
>
⎟
⎠
⎞
⎜
⎝
⎛
−x
,
32
3
1
3
1
⎟
⎠
⎞
⎜
⎝
⎛
>
⎟
⎠
⎞
⎜
⎝
⎛
−x
, |x – 2| < 3
⎢
⎢
⎢
⎢
⎣
⎡
⎩
⎨
⎧
−>
<−
⎩
⎨
⎧
<
≥−
⇔
1
02
5
02
x
x
x
x
x ∈ (-1; 5).
№ 1218
1) 555
5,13
2
<
++ xx
,
2
3
5,13
55
2
<
++ xx
, x
2
+ 3x + 1,5 < 3/2,
x
2
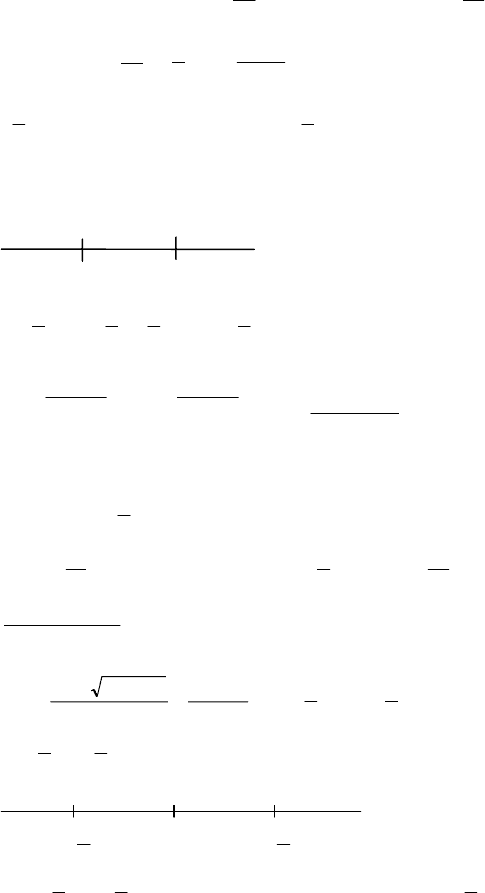
+ 3x < 0, x(x + 3) < 0
+
+
–
-3 0
-3 < x < 0.
2)
12,0
76
2
≥
+− xx
,
076
2,02,0
2
≥
+− xx
, x
2
–6x+7 ≤ 0,
[
]
23;23 +−∈x .
№ 1219
1)
3
2
1
1
393 ≥
−
+
x
x
,
3
1
121
333 ≥⋅
−+ xx
,
3
1
3
33 ≥
x
, 3х ≥ 1/3,
9
1
≥
x ;
2) 3
x+1
+ 3
x-1
< 10, 3
x
(3 + 3
-1
) < 10, 10
3
10
3 <⋅
x
, 3
x
< 3, x < 1.
№ 1220
1) 522842
4
3
2
12
>⋅+−
−−
x
xx
, 2
2x
– 2
2x-2
+ 2
2x-4
> 52, 2
2x-4
(2
4
–2
2
+ 1) > 52,
2
2x-4
⋅ 13 > 52, 2
2x-4
> 4, 2
2x-4
> 2
2
, 2x – 4 > 2, 2x > 6, x > 3;
197
2) 2
x+2
– 2
x+3
+ 5
x-2
> 5
x+1
+ 2
x+4
, 2
x+2
– 2
x+3
– 2
x+4
> 5
x+1
– 5
x-2
,
4 ⋅ 2
x
– 8 ⋅ 2
x
– 16 ⋅ 2
x
> 5 ⋅ 5
x
-
25
1
⋅ 5
x
,
()
⎟
⎠
⎞
⎜
⎝
⎛
−>−−
25
1
5516842
xx
,
()
25
24
45202 ⋅>−
xx
,
2025
124
5
2
⋅
−<
⎟
⎠
⎞
⎜
⎝
⎛
x
,
248,0
5
2
−<
⎟
⎠
⎞
⎜
⎝
⎛
x
— решений нет, т.к.,
0
5
2
>
⎟
⎠
⎞
⎜
⎝
⎛
x
для всех х.
№ 1221
1) 13,3
6
2
<
+ xx
,
06
3,33,3
2
<
+ xx
, т.е. х
2
+ 6х < 0, x(x + 6) < 0
+
+
–
–
6
0
-6 < x < 0;
2)
2
1
4
1
2
>
⎟
⎠
⎞
⎜
⎝
⎛
−xx
,
2
1
2
1
2
22
>
⎟
⎠
⎞
⎜
⎝
⎛
− xx
, т.е. 2х – 2х
2
< 1, 2x
2
– 2x + 1 > 0,
x ∈ R, т.к. D < 0;
3)
14,8
116
3
2
<
++
−
xx
x
,
0
116
3
4,84,8
2
<
++
−
xx
x
, 0
116
3
2
<
++
−
xx
x
,
x
2
+ 6x + 11 > 0 при любых х, т.к. D < 0, x – 3 < 0, x < 3.
Ответ: x < 3.
4)
02
2
1
212
32
12
≥+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
+
+
x
x
, 2
2x
⋅ 2 – 21 ⋅ 2
-2x-3
+ 2 ≥ 0,
022
8
21
22
22
≥+⋅−⋅
− xx
, 2
2x
= a,
a
x
1
2
2
=
−
, a > 0, 02
8
21
2 ≥+−
a
a ,
0
8
211616
2
≥
−+
a
aa
равносильно (16a
2
+ 16a – 21)8a ≥ 0.
Найдем корни трехчлена 16a
2
+ 16a – 21,
16
208
16
336648
2,1
±−
=
+±−
=a
,
4
7
,
4
3
21
−== aa ,
0
4
7
4
3
≥
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
− aaa ,
–
–
+
+
4
7
−
4
3
−
0
⎟
⎠
⎞
⎢
⎣
⎡
+∞
⎥
⎦
⎤
⎢
⎣
⎡
−∈ ;
4
3
0;
4
7
Ua
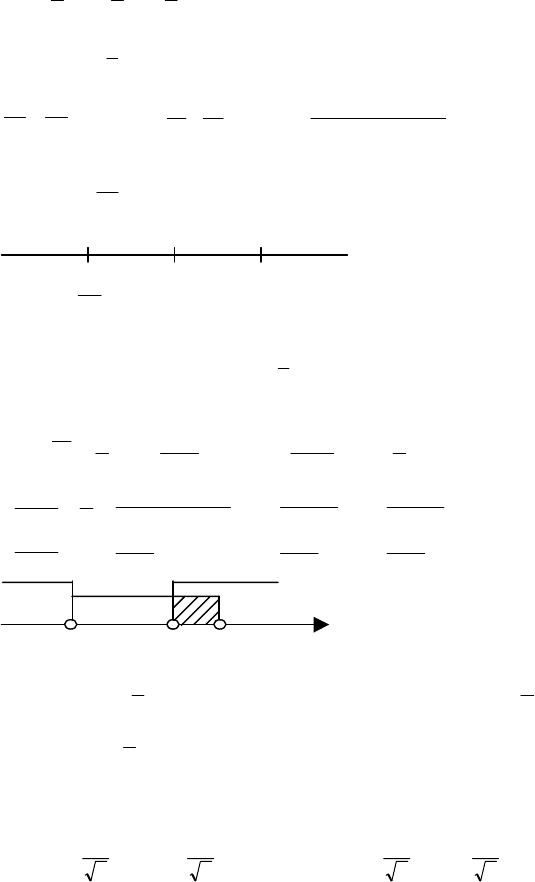
т.к. а > 0, то решением является
⎟
⎠
⎞
⎢
⎣
⎡
∞+∈ ;
4
3
a
198
4
3
log
2
1
;
4
3
2
2
2
≥≥ x
x
.
5)
06
3
1
353
32
34
≥+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−
x
x
, 3
4
⋅ 3
-3x
– 35 ⋅ 3
3x-2
+ 6 ≥ 0, 3
3x
= a, a > 0,
06
9
353
4
≥+⋅− a
a
,
06
9
3581
≥+− a
a
, 0
9
5435981
2
≥
+−⋅
a
aa
,
(-35
a
2
+ 54a + 729)a ≥ 0, (35a
2
– 54a – 729)a ≤ 0,
()
0
7
27
4,5 ≤
⎟
⎠
⎞
⎜
⎝
⎛
+− aaa ,
–
–
+
+
7
27
−
0 5,4
т.к. a > 0, то решением является 0 < a ≤ 5,4, 3
3x
≤ 5,4,
4,5log
3
3
33 ≤
x
, 3x ≤ log
3
5,4, 5log
3
1
1
3
−≤x .
№ 1222
1)
9
1
3
2
1
log
2
<
+
−
x
x
,
2
2
1
log
2
−<
+
−
x
x
,
4
1
log
2
1
log
22
<
+
−
x
x
⎪
⎩
⎪
⎨
⎧
>
+
−
<
+
−
0
2
1
4
1
2
1
x
x
x
x
()
(
)
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
+
−
<
+
+−−
0
2
1
0
24
214
x
x
x
xx
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
+
−
<
+
−
0
2
1
0
24
63
x
x
x
x
(
)
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
+
−
<
+
−
0
2
1
0
24
23
x
x
x
x
–
2 21
2)
()
5
1
5
5,34log
2
2
>
+− xx
,
(
)
1
5,34log
55
2
2
−
+−
>
xx
,
()
2
1
log5,34log
2
2
2
>+− xx ,
⎪
⎩
⎪
⎨
⎧
>+−
>+−
05,34
2
1
5,34
2
2
xx
xx
⎪
⎩
⎪
⎨
⎧
>+−
>+−
05,34
034
2
2
xx
xx
()()
⎪
⎩
⎪
⎨
⎧
>
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
>−−
0
2
1
2
2
1
2
031
xx
xx
(
)
(
)
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+∞+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−∞−∈
+∞∞−∈
;
2
1
2
2
1
2;
;31;
U
U
x
x
x ∈ (-∞;1)
U
(3;+∞).
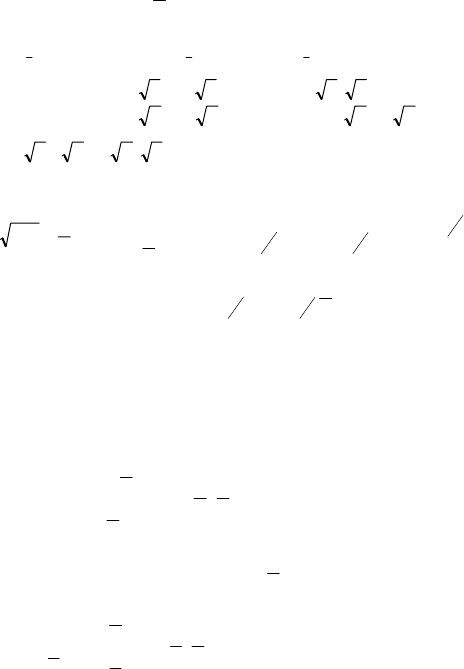
199
№ 1223
1) log
6
(2 – x) < log
6
(2x + 5)
⎪
⎩
⎪
⎨
⎧
>+
>−
+<−
052
02
522
x
x
xx
;
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−>
<
−>
2
5
2
1
x
x
x
x ∈ (-1; 2);
2)
()
12log
2
3
1
−≥−x
,
(
)
3log2log
3
1
2
3
1
≥−x
,
⎪
⎩
⎪
⎨
⎧
>−
≤−
02
32
2
2
x
x
;
()
(
)
()()
⎪
⎩
⎪
⎨
⎧
>+−
≤+−
022
055
xx
xx
[
]
()()
⎪
⎩
⎪
⎨
⎧
+∞−∞−∈
−∈
;22;
5;5
Ux
x
[
)
(
]
5;22;5 U−−∈x .
№ 1224
1)
2
1
lg <x
,
⎪
⎩
⎪
⎨
⎧
<
≥
4
1
lg
0lg
x
x
;
⎪
⎩
⎪
⎨
⎧
<
≥
4
1
10lglg
1
x
x
;
⎪
⎩
⎪
⎨
⎧
<
≥
4
1
10
1
x
x
⎟
⎟
⎠
⎞
⎢
⎣
⎡
∈
4
1
10;1x
2) log
1/2
x < log
1/2
(2x + 6) + 2,
()
62
4
1
loglog
2
1
2
1
+< xx
,
⎪
⎩
⎪
⎨
⎧
+>
>+
>
624
062
0
xx
x
x
⎪
⎩
⎪
⎨
⎧
>
−>
>
3
3
0
x
x
x
x ∈ (3; +∞).
№ 1225
1) log
0,5
(1 + 2x) > -1, log
0,5
(1 + 2x) > log
0,5
2
⎩
⎨
⎧
<+
>+
221
021
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<
−>
2
1
2
1
x
x
⎟
⎠
⎞
⎜
⎝
⎛
−∈
2
1
;
2
1
x
;
2) log
3
(1 – 2x) < -1, log
3
(1 – 2x) < log
3
3
1
,
⎪
⎩
⎪
⎨
⎧
<−
>−
3
1
21
021
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
<
3
1
2
1
x
x
⎟
⎠
⎞
⎜
⎝
⎛
∈
2
1
;
3
1
x .
№ 1226
1) log
0,5
(x
2
– 5x + 6) > -1
⎪
⎩
⎪
⎨
⎧
<+−
>+−
265
065
2
2
xx
xx
()
(
)
()( )
⎩
⎨
⎧
<−−
>−−
041
023
xx
xx
(
)
(
)
()
⎩
⎨
⎧
∈
+∞∞−∈
4;1
;32;
x
x
U
x ∈ (1; 2)
U (3; 4);
