Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


251
Розділ IV. Диференційне числення функції однієї змінної
=
2
2
3
231
(1)(2)
xx
xx
.
б)
y = y =
(sin
x
)
cos x
;
ln
y =
ln((sin
x
)
cos x
)
=
cos
x
ln(sin
x
),
(ln ) (cos ln(sin )) (cos ) lnsin cos (lnsin )yxx xxxx
ccc c
= –
sin
x
lnsin
x +
cos
x
1
sin x
cos
x
,
1
y
y
c
= –
sin
x
lnsin
x +
2
cos
sin
x
x
,
y
c
= y
(
–
sin
x
lnsin
x +
2
cos
sin
x
x
)
=
(sin
x
)
cos x
(
–
sin
x
lnsin
x +
2
cos
sin
x
x
)
.
4.1.4. Приклади для самостійного розв’зку
Приклад 4.4.
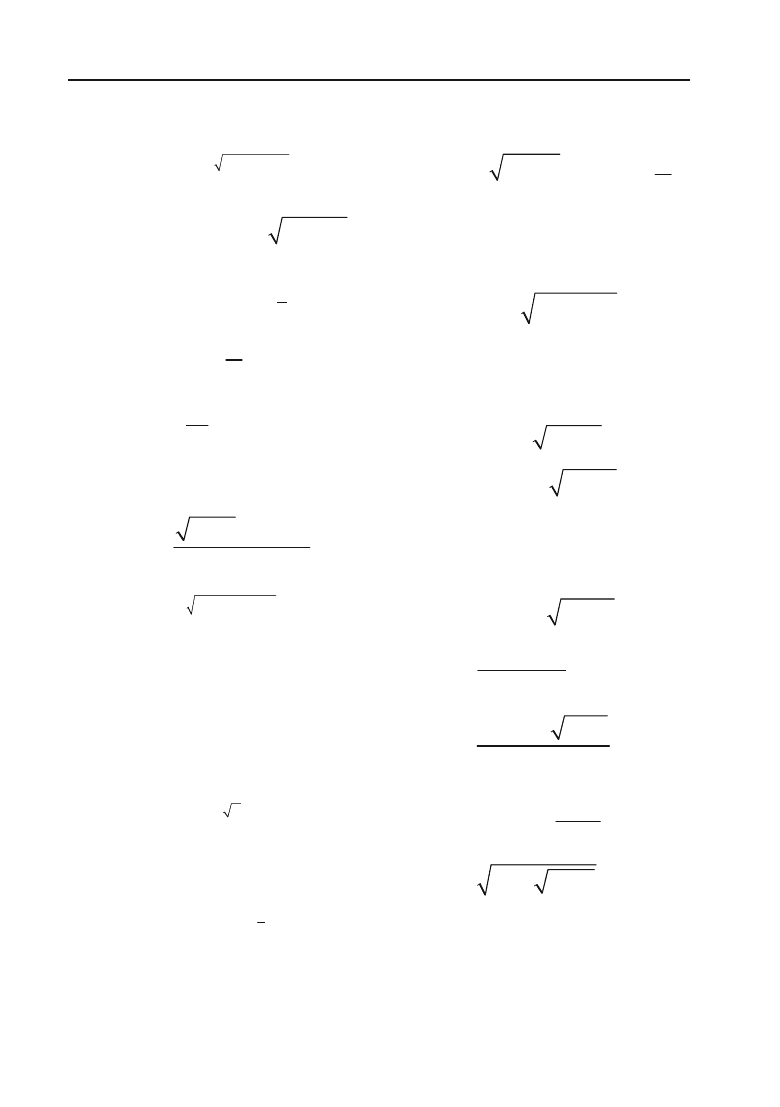
Знайти похідні (
а
,
b
,
c
– сталі):
1)
2
2
1
1
xx
y
x
;2)
2
1 x
y
x
;
3)
3
1
y
x
;4)
y
= ctg
3
2
1
x
;
5)
y
=
x
4
tg
2
x
;6)
y
= sin
2
(cos
x
);
7)
y
=
e
cosx
sin
2
x
;8)
y
= log
3
(
x
2
–
1);
9)
y
=
x
arccos
x
; 10)
y
= ln(arccos2
x
);
11)
y =
(1 + ln sin
x
)
2
; 12)
y
= arcsin
2
(ln(
a
2
+
x
2
));
13)
y
=
arcctg
3
1
x
x
; 14)
y
= sin
2
1lnx
x
§·
¨¸
©¹
;
15)
y
=
2
x
2
1x
+ ln(
2
1xx
); 16)
y
= (
x
2
+ 4)arctg
2
x
;
252
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
17)
3
arcsin 2
2
x
y
; 18)
y
= arсctg
3
e
–5x
;
19)
arctg 1 ln(2 3)
x
ye
; 20)
y
=
x
2
4 x
+ 4arcsin
2
x
;
21)
y
= 2ln(2
x
– 3
2
14
x
) – 6arcsin2
x
; 22)
y
= (
x
2
+
1)
sinx
;
23)
y
= ln
x
x
; 24)
y
= (1 – 4
x
3
)
cos4x
;
25)
y
= (1 – ctg3
x
)
1
x
; 26)
y
= lnsin
3
3
arctg
x
e
;
27)
y
= arctg
2
1
x
; 28)
y
=
e
arcsin2x
;
29)
ln
2
x
x
y
; 30)
y
= arccos
13
x
;
31)
y
=
x
3
arctg
x
3
; 32)
y
= ln(
x
sin
x
2
1
x
);
33)
4
5
2(3 )
(1)
x
x
y
x
; 34)
y
=
x
lnx
;
35)
2
ln
()
ax bx c
ye
; 36)
y
= ln arctg
2
1 x
;
37)
y
= arctg(ln(
ax
+
b
)); 38)
arcsin4
14
x
y
x
;
39)
y
= 10
xtgx
; 40)
2
3
3
(2) 1
(5)
xx
y
x
;
41)
(2 )
x
y
x
; 42)
y
= ln arcсtg
1
1 x
;
43)
y
= sin
2
x
sin
x
2
; 44)
3
13yxx
;
45)
2
ct
g
(
t
g
2
)
x
yx
.

253
Розділ IV. Диференційне числення функції однієї змінної
§4.2. Похідна неявної функції. Параметричне завдання
функції. Диференціювання функції, заданої параметрично.
Похідні вищіх порядків
4.2.1. Похідна неявної функції
Якщо незалежна змінна
х
і функція у зв’язані рівнянням виду
f
(
x
,
y
) = 0, яке не розв’язане відносно
у
, то
у
називається
неявною
функцією х
.
Незважаючи на те, що рівняння
f
(
x
,
y
) = 0 не розв’язане відносно
у
, можна знайти похідну від
у
по
х
. Прийом для знаходження по+
хідної в цьому випадку полягає в тому, що обидві частини рівняння
f
(
x
,
y
) = 0 диференціюємо по
х
з врахуванням, що
у
є функцією
x
, і
із одержаного рівняння визначаємо
y
c
.
Приклад 4.5.
Знайти похідну
y
c
функції
х
:
а)
x
3
+ y
3
–
3
axy
= 0;
б)
x
y
= y.
Розв’язок.
a)
33
()()(3 )0xy axy
cc cc
,
3
x
2
+
3
y
2
y
c
–
3
a
(
x
c
y + x
y
c
) = 0,
3
x
2
+
3
y
2
y
c
–
3
ay –
3
ax
y
c
= 0,
y
2
y
c
– ax
y
c
= ay – x
2
,
y
c
(
у
2
– ах
)
= ау – х
2
,
2
2
a
y
x
y
y
ax
c
.
б)
x
y
= y
x
.
Прологарифмуємо обидві частини даного рівняння (за основою
е
), потім продиференціюємо по
х
, розглядаючи
у
як функцію
х
.
ln
x
y
=
ln
y
x
,
y
ln
x = x
ln
y
,
(ln) (ln)
x
x
y
xx
y
cc
,

254
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4.2.2.Параметричне завдання функції
В геометрії часто вживається так званий параметричний спосіб
задання рівняння кривої. Криву лінію можна розглядати як геомет+
ричне місце послідовних положень рухомої точки, а координати х і
у цієї точки виразити в вигляді неперервної функції допоміжної
змінної
t
, яка називається
параметром
. Плоска крива в такому ви+
падку визначається двома рівняннями:
(),
().
x
t
y
t
M
\
®
¯
Наприклад. Крива задана параметричними рівняннями
cos ,
sin .
x
at
y
bt
®
¯
02t
S
dd
є еліпс.
Похідна функції
(),
().
x
t
y
t
M
\
®
¯
що задана параметричними рівняннями, знаходяться за формулою:
ln (ln ) ln (ln )
y
x
y
xx
y
x
y
cccc
,
11
ln 1ln
y
x
yy
x
y
xy
cc
,
ln
y
xxy
x
c
=
ln
y
yxy
y
c
,
y
c
xy
ln
x + y
2
= xy
ln
y + x
2
y
c
,
y
c
xy
ln
x – x
2
= xy
ln
y – y
2
,
y
c
(
xy
ln
x – x
2
)
= xy
ln
y – y
2
,
y
c
=
2
2
ln
ln
xy y y
xy
xx
=
(ln )
(ln )
y
xyy
xy x x
.

255
Розділ IV. Диференційне числення функції однієї змінної
x
y
c
=
t
t
y
x
c
c
.
Похідна другого порядку визначається за формулою:
2
2
d
y
dx
=
dy
dx
c
=
d
y
dt
dx
dt
c
.
Приклад 4.6.
Знайти при
4
t
S
похідні
dy
dx
та
2
2
dy
dx
функції
cos sin
sin cos
x
tt t
y
tt t
®
¯
.
Розв’язання.
1)
dy
dx
=
t
t
y
x
c
c
.
Знайдемо
(cos sin )
tt
x
tt t
cc
=
–sin
t +
sin
t + t
cos
t = t
cos
t
,
(sin cos )
tt
y
tt t
cc
=
cos
t –
cos
t + t
sin
t = t
sin
t
,
dy
dx
=
sin
cos
tt
tt
= tg
t
,
dy
dx
4
t
S
=
tg
4
S
=
1.
2)
2
2
d
y
dx
=
(')d
y
dt
dx
dt
=
(tg )
cos
d
t
dt
tt
=
2
1
cos
cos
t
tt
=
3
1
costt
.

256
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2
2
d
y
dx
4
t
S
=
3
1
cos
44
SS
=
3
1
2
4
2
S
§·
¨¸
©¹
=
1
22
4
8
S
=
16
2
S
=
82
S
.
4.2.3. Похідні вищих порядків
Похідна
y
c
від функції y в загальному випадку є функцією х.
Якщо від цієї функції
y
c
знайти похідну, то одержимо похідну дру+
гого порядку, або другу похідну функції
y
=
f
(
x
), і вона позначається
y
cc
або
()
f
x
cc
, або
2
2
dy
dx
.
Аналогічно визначаються похідні будь+якого порядку:
Похідна третього порядку:
() ()
yyf
x
cc c ccc ccc
3
3
dy
dx
.
Похідна четвертого порядку:
()
y
ccc c
= y
IV
= f
IV
(
x
)
=
4
4
dy
dx
.
Похідна
n
го порядку:
1
()
n
y
c
= y
n
= f
n
(
x
)
=
n
n
dy
dx
.
Для знаходження похідної будь+якого вищого порядку від зада+
ної функції потрібно послідовно знаходити всі її похідні нижчих
порядків.
Для добутку двох функцій можна одержати похідну будь+якого
n
+го порядку, користуючись формулою Лейбніца:
(
uv
)
(n)
= u
(n)
v + nu
(n–1)
v
c
+
(1)
2!
nn
u
(n–2)
v
cc
+ … +
+
( 1)( 1)...( 1)
!
nn n n k
k
u
(n–k)
v
(k)
+ … + n
u
c
v
(n–1)
+ uv
(n)
.

257
Розділ IV. Диференційне числення функції однієї змінної
Приклад 4.7.
y =
3
x
4
+
5
x
3
–
4
x
2
+ 8
.
Знайти
у
(4)
.
Розв’язок.
y
c
=
12
x
3
+
15
x
2
–
8
x
;
y
cc
=
()
y
cc
=
36
x
2
+
30
x –
8;
y
ccc
=
()
y
cc c
=
72
x +
30;
y
(4)
=
(3)
()y
c
=
72
.
Приклад 4.8.
y =
sin
2
x
,
знайти
у
(5)
.
Розв’язок.
y
c
=
2sin
x
cos
x =
sin2
x
;
y
cc
=
()
y
cc
=
2cos2
x;
y
(3)
=
()
y
cc c
=
–4sin2
x;
y
(4)
=
(3)
()y
c
=
–8cos2
x;
y
(5)
=
(4)
()y
c
=
16sin2
x;
Приклад 4.9.
y = x
m
.
Знайти
y
(k)
.
Розв’язок.
y
c
= mx
m–1
;
y
cc
=
()
y
cc
= m
(
m–
1)
x
m–2
;
y
ccc
= m
(
m
–1)(
m
–2)
x
m–3
;
y
(4)
= m(m
–1)(
m
–2)(
m
–3)
x
m–4
;
………………………
y
(k)
= m
(
m
–1)(
m
–2) … (
m–k
+1)
x
m–k
.
4.2.4. Приклади для самостійного розв’язку
Приклад 4.10.
Знайти похідні від неявно заданої функції:
1)
y
ln
x
–
x
ln
y
=
x
+
y
;2)
x
sin
y
–
y
cos
x
= 0;
3)
e
x+y
–
xy
= 0; 4)
e
xy
– (
x
+
3
y)
= 0;
5)
y
sin
x
+ cos(
x
–
y
)
=
cos
y
;6)
ln
x
y
–
x
+ 2
y
=
0;
7)
e
xy
–
x
2
+
y
2
= 0.
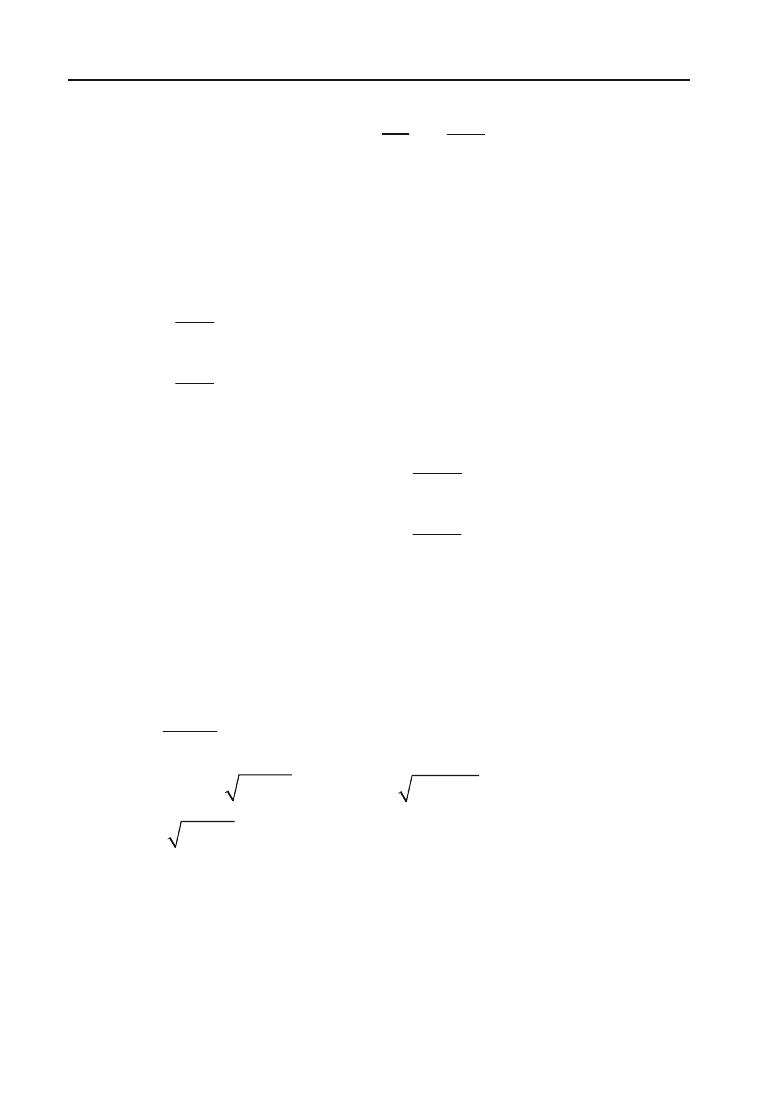
258
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 4.11.
Знайти похідні
dy
dx
та
2
2
dy
dx
від функцій, що зада+
но параметрично.
1)
2
3
1xt
y
tt
®
¯
;2)
(sin)
(1 cos )
x
at t
y
at
®
¯
;
3)
1
1
t
x
t
t
y
t
°
°
®
°
°
¯
;4)
2
ln(1 )
arctg
xt
y
tt
®
¯
;
5)
(1 sin )
cos
x
y
M
M
MM
®
¯
;6)
2
2
2
1
1
1
t
x
t
t
y
t
°
°
®
°
°
¯
;
7)
sin
cost
t
t
xe t
ye
®
¯
.
Приклад 4.12.
Знайти похідні другого порядку від функції
а)
2
1
1
y
x
;б)
y =
(1 +
x
2
)arctg
x
;
в)
2
ln( 1 )
y
xx
;г)
22
y
ax
;
д)
y =
2
1 x
arcsin
x.

259
Розділ IV. Диференційне числення функції однієї змінної
§4.3. Механічний та геометричний зміст похідної.
Рівняння дотичної та нормалі до кривої
4.3.1. Механічний та геометричний зміст похідної.
Джерелом диференційного числення стали, як відомо, два питання:
1) про відшукання швидкості в разі довільного закону руху;
2) про відшукання дотичної до довільної кривої.
Обидва вони привели до однієї й тієї задачі, яку було покладено
в основу диференційного числення. Ця задача полягає в тому, щоб
за даною функцією
f
(
x
) відшукати іншу функцію
()
f
x
c
, яка дістала
назву похідної і являє собою швидкість зміни функції
f
(
x
) щодо зміни
аргументу.
У механіці відповідна задача формулюється так: знайти швидкість
тіла, що рухається за законом
S
=
f
(
t
), у деякий момент часу
t
. Вва+
жаємо, що відстань
S
і час
t
— фізичні величини, які можна виміряти.
Нехай за час від
t
до
tt'
тіло пройшло шлях
()SS
f
tt' '
.
Тоді
()()S
f
tt
f
t' '
.
Середня швидкість тіла, що рухається вздовж деякої лінії, визна+
чається за формулою:
V
сер
=
S
t
'
'
=
()()ft t ft
t
'
'
.
Щоб знайти миттєву швидкість
V
такого тіла, потрібно перейти
до границі відношення
S
t
'
'
при
0t'o
.
V
=
0
lim
t
'o
S
t
'
'
=
0
lim
t
'o
()()
f
ttft
t
'
'
=
()
f
t
c
.
Миттєвою швидкістю тіла, що рухається вздовж лінії S
=
f
(
t
),
називається похідна функції
S
=
f
(
t
) за часом
t
:
V
=
dS
dt
=
()
f
t
c
.
260
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 4.13.
Точка рухається по кубічній параболі 12
у = х
3
.
Яка
із її координат змінюється швидше?
Розв’язок.
Вважаючи в рівнянні параболи
у
складною функцією
від часу
t
і диференціюючи його по
t
, одержуємо:
12
dy
dt
= 3
х
2
dx
dt
.
Звідси знаходимо відношення швидкості ординати і абсциси:
dy
dx
:
dx
dt
=
2
4
x
.
При |
х
| < 2
це відношення буде менше 1, при |
х
| = 2 — дорівнює 1
і при |
х
| > 2 воно буде більше 1.
Отже:
1) при
–
2 <
x
<2 ордината змінюється швидше абсциси;
2) при
2x r
швидкість зміни абсциси і ординати однакові;
3) при
x
< –2
і
x
> 2 ордината змінюється швидше абсциси.
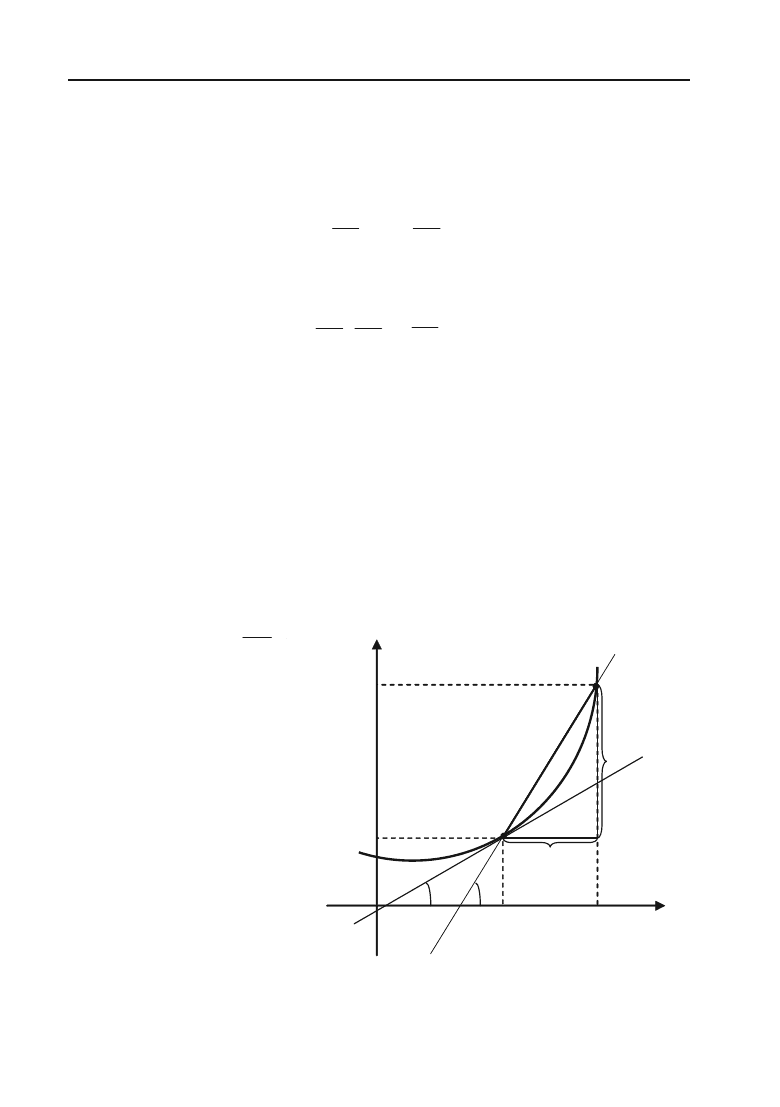
Геометричний зміст похідної
Нехай дано функцію
у = f
(
х
), графік якої наведено на рис. 4.1.
Відношення
y
x
'
'
дорівнює тангенсу кута
E
, утвореного січною,
що проходить крізь
точки
Р
та
Q
, які мають
відповідно абсциси
х
та
x
x'
, із додатним
напрямом вісі
Ох.
Якщо приріст
0
x
'o
, то точка
Q
прямує до точки
Р
, а
кут
E
— до кута
D
,
утвореного дотичною
Y
f(x+
x'
)
f(x)
0
x
x+
x'
X
D
E
x'
y'
y = f
(
x
)
P
Q
Дотична
Січна
Рис. 4.1.
