Конверський А. Є. Логіка (традиційна та сучасна)

Подождите немного. Документ загружается.

Книга перша. ТРАДИЦІЙНА ЛОГІКА

191

Наприклад:

І 1) «Будь-який злочин є суспільно небезпечним вчин-

ком» – істинне і

2) «Жоден вчинок не є суспільно небезпечним вчин-

ком» – хибне; і

ІІ 1) «Будь-який злочин є посадовим» – хибне, і

2) «Жоден злочин не є посадовим» – те ж хибне.

Відношення підпротивності

(субконтрарності)

Відношення підпротивності (субконтрарності) має місце

між судженнями Isp та Osp.

Суть цього відношення полягає в тому, що судження

Isp та Osp можуть бути разом істинними, а хибними –

ні. В крайньому випадку одне з них буде істинним.

Наприклад:

І 1) «Деякі вироки є обґрунтованими» і

2) «Деякі вироки не є обґрунтованими» – одибва

судження істинні;

ІІ 1) «Деякі злочини є суспільно небезпечними вчинками» і

2) «Деякі злочини не є суспільно небезпечними вчин-

ками».

У цих прикладах судження Isp – є істинним, а су-

дження Osp – хибним.

Суперечливими є пари суджень: Asp та Osp i

Esp та Isp.

Відношення протиріччя

Відношення протиріччя передбачає, що з двох супе-

речливих суджень одне обов’язково буде істинним, а

друге обов’язково буде хибним.

Наприклад: «Будь-який злочин є суспільно небезпечним

вчинком» Asp – істинне. А утворене від нього судження

«Деякі злочини є суспільно небезпечними вчинками» Osp

буде хибним.

Отже, так як логічні відношення між поняттями врахо-

вують лише їх екстенсіональні, обсягові характеристики,

так і логічні відношення між атрибутивними судженнями

враховують лише їх екстенсіонали, значення («істина»,

А. Є. Конверський. ЛОГІКА

192

«хиба»). Тобто, ці відношення не враховують «що і про що

говориться у судженнях».

Коли відомо, що Asp є істинним, то, знаючи дефініції

логічних відношень між судженнями, ми однозначно мо-

жемо стверджувати, що Isp буде істинним, а Osp та Esp

буде хибним. Або, коли дано, що Asp – хибне, то Osp бу-

де істинним, а Isp та Esp буде будь-яким.

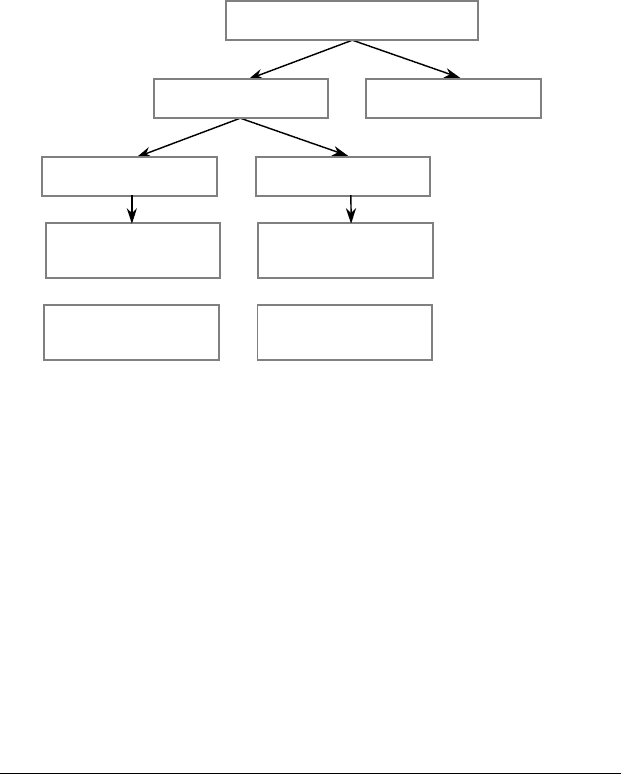
Розглянуті відношення між атрибутивними судженнями

можна зобразити такою схемою:

Атрибутивні судження

Порівнювані Непорівнювані

Сумісні Несумісні

відношення

підпорядкування

відношення

протиріччя

відношення

підпротивності

відношення

противності

Значення дефініцій логічних відношень між атрибутив-

ними судженнями необхідне при побудові безпосередніх

умовиводів. Йдеться про безпосередні умовиводи, що базу-

ються на логічних відношеннях між атрибутивними су-

дженнями, або як їх іноді ще називають «умовиводи за

«логічним квадратом».

Знання логічних відношень між атрибутивними су-

дженнями також дає змогу зрозуміти суть такої логічної

операції, як «заперечення атрибутивного судження».

З а п е р е ч е н н я м судження називається така

логічна операція, яка полягає у такому перетворенні

логічного змісту судження, у результаті якого отри-

мують судження, що знаходиться у відношенні контра-

дикторності до вихідного. Наприклад:

1. «Всі мої приятелі мають вищу освіту» і

2. «Неправильно, що всі мої приятелі мають вищу освіту».

Книга перша. ТРАДИЦІЙНА ЛОГІКА

193

По суті судження 2, коли його взяти без зовнішньо-

го заперечення («неправильно»), еквівалентне судженню

«Деякі мої приятелі не мають вищої освіти» Osp.

При запереченні атрибутивного судження змінюються

його кількість і якість. Так, заперечуючи загальне отриму-

ємо часткове (і навпаки), а заперечуючи стверджувальне

отримуємо заперечувальне (і навпаки).

5. Тлумачення атрибутивних суджень

мовою логіки предикатів

У традиційній логіці структура атрибутивних суджень

фіксується схемою «Всі S є Р» або символом Asp тощо.

Очевидно, що тут поряд з елементами формалізації є фра-

гменти природної мови, що спричиняє певні вади тлума-

чення структури атрибутивних суджень.

Сучасна логіка знаходить для цього більш ефективні за-

соби, а саме мову логіки предикатів.

Мова логіки предикатів (як і будь-яка мова логіки)

включає в себе:

1) алфавіт (сукупність вихідних символів: а) нелогіч-

них, б) логічних, в) технічних) і

2) правила побудови з елементів алфавіту правильно

побудованих формул (ППФ)

І. Алфавіт

1. Предметні (індивідні) константи: а, в, с, а

, в

, с

,в

, с

... . Індивідні константи – це власні імена природної

мови («Арістотель», «Дніпро», «Юпітер» тощо). При пере-

кладі виразів природної мови на мову логіки предикатів іме-

на замінюються предметними константами так, щоб однакові

імена відповідали однаковим символам із списку індивідних

констант, а різні імена – різним.

2. Предметні (індивідні) змінні: x, y, z, x

, y

, z

, x

, y

… .

Якщо предметні константи зв’язуються у відповідних

межах із конкретними власними іменами, то предметні

змінні можуть замінювати будь-яке ім’я з предметної об-

Вирази побудовані у межах логіки предикатів, називають «формулами» то-

му, що їх можна ототожнювати, розрізняти, порівнювати лише за зовнішніми

ознаками, тобто за формою.

А. Є. Конверський. ЛОГІКА

194

ласті того контексту, який аналізується. Тому предметні

змінні використовуються для формалізації атрибутивних

суджень з кванторними словами («Всі», «Деякі», «Кожен»,

«Іноді» тощо).

3. Предметно-функціональні константи : f

, q

, h

, f

, q

,, h

... .

Верхній індекс n вказує на місність константи, а ниж-

ній – на порядковий номер. В арифметиці до предметних

функторів відносяться операції над числами: « √ », (+), sin

тощо. У природній мові предметними функторами є слова,

які з одними предметами зіставляють інші («столиця»,

«ріст», «відстані від ... до ...» тощо).

4. Предикаторні константи: P

, Q

, R

, S

, P

, Q

, S

, P

, Q

, R

, S

... .

Верхній індекс вказує на місткість константи, а ниж-

ній – на порядковий номер. Якщо із константи відомо, що

предикаторна константа одномісна, то верхній індекс опу-

скається. У природній мові предикатори різної місності

представлені словами: «електропровідний», «більше», «ро-

весник», «держава» тощо.

5. Логічні символи:

а) логічні зв’язки: &, ∨, ⊃, ↔,  (або ( — ));

б) кванторні символи:

— квантор загальності – ∀ х («для будь-якого»),

— квантор існування – ∃ х («існує»).

6. Технічні символи:

— ліва і права дужки, кома.

ІІ. Правила побудови виразів

у мові логіки предикатів

а) Дефініція терма

1. Довільна предметна константа є термом.

2. Довільна предметна змінна є термом.

3. Якщо Ф – n-містка предметно-функціональна конс-

танта, а t

, t

, ... t

– терми, то вираз Ф (t

, t

, ... t

) є

термом.

4. Ніщо, крім зазначеного в пунктах 1–3, не є термом у

мові логіки предикатів.

Вирази у пунктах 1 та 2 відносяться до простих тер-

мів, а вирази, зазначені у пункті 3, – до складних.

Книга перша. ТРАДИЦІЙНА ЛОГІКА

195

Візьмемо вираз f

(x, a)). Відповідно до наведеної де-

фініції терма встановимо, чи є даний вираз термом, чи ні.

(x, a)) = Ф(t

) згідно з пунктом 3 (тобто, одномісна

предметно-функціональна константа);

(x, a) = t

(тобто є термом);

(x, a) має вид Ф (t

, t

Ф відповідає функціональній константі – q

; t

є x –

тобто термом згідно з пунктом 1 визначення терма, а t

а, тобто термом згідно з пунктом 3 визначення терма. Ви-

ходить, що q

, t

) є термом згідно з пунктом 3.

Тоді весь вираз: f

(x, a)) є термом.

Можна припустити, що даний терм є формалізацією та-

кого фрагмента природної мови: q відповідає двомісному

функтору (+); f – одномісному функтору (√); а відповідає

простому імені «5». У такому випадку вираз f

(x,a))

буде формалізацією імені: « √ х + 5».

Якщо візьмемо вираз Р

(x, a)), то він не є термом

оскільки починається з предикаторної константи.

б) Дефініція формули:

1. Якщо П – n-містка предикаторна константа, а t

, t

... t

– терми, то вираз П (t

, t

, ... t

) – формула.

2. Якщо А – формула, то А є формулою.

3. Якщо А і В – формули, то (A & B), (A ∨ B), (A ⊃ B),

(A ↔ B) – формули.

4. Якщо А – формула, а х – предметна змінна, то ∀

хА і ∃ хА є формулами.

5. Ніщо крім перерахованого в пунктах 1–4 не є фор-

мулами.

Формули, які відповідають пункту 1 дефініції, назива-

ють елементарними або атомарними, а в пунктах 2–4 –

складними або молекулярними.

Елементарною формулою, наприклад, буде вираз

(х, f

(a)) .

– двомісна константа, а після неї в дужках знахо-

диться два терми х і f

(а).

А вираз Q

(x, f

(a)) не є формулою, оскільки Q

– од-

номісна предикаторна константа, але після неї стоїть два

терми х і f

(a).

На мову логіки предикатів можна перекласти атри-

бутивні судження, в яких:

а) стверджується наявність властивості у окремого

предмета;

А. Є. Конверський. ЛОГІКА

196

б) йдеться про існування якогось об’єкта, що задово-

льняє деяку умову;

в) стверджується, що деякій умові задовольняє будь-

який об’єкт предметної області.

У випадку а), тобто коли формалізується одиничне ат-

рибутивне судження, користуємося формулою П

(t), де П

є одномісна предикаторна константа, що відповідає знаку

властивості, а t – терм, що відповідає імені предмета. На-

приклад, маємо атрибутивні судження: «Тарас Шевченко

– поет». Перекладом його на мову логіки предикатів буде

вираз: «Р (а)»; «Батько мого приятеля – лікар» – Q (f

(a)), де f – це одномісна предикаторна константа, що від-

повідає предметному функтору «батько», а – терм «мій

приятель», а Q – одномісна предикаторна константа, що

відповідає властивості «бути лікарем»;

У ситуації б), а саме, коли формалізуються атрибутивні

судження про існування деяких предметів, то використо-

вують формулу ∃х А(х), де х – предметна змінна, що про-

бігає по області об’єктів, про які йдеться у висловлюванні,

а А(х) – формула, яка фіксує, що х задовольняє умову А.

Наведемо приклади перекладу цього типу атрибутивних

суджень мовою логіки предикатів:

1. «Хтось винайшов радіо» – ∃х Р(х).

2. «Деякі поети є лауреатами» – ∃х Q(x).

3. «Деякі мої приятелі не мають вищої освіти» –

∃х  F(x).

Треба пам’ятати те, що якщо областю значення для

предметної змінної береться множина предметів, які фік-

суються предикатором у позиції логічного підмета, то фо-

рмула, яка буде перекладом атрибутивного судження мо-

вою логіки предикатів буде мати у своєму складі простий

предикат виду Р(х) чи Q(x) і т.д.

Це очевидно з наведених вище прикладів: ∃х Р(х), ∃x

Q(x), ∃х  F(x).

Якщо змінити область значення предметної змінної, а

саме вважати її як множину будь-яких об’єктів, то вираз

логіки предикатів, як переклад атрибутивного судження,

включатиме в себе складний предикат

(S (x) ∧ P(x)).

Це ж стосується формалізації загальностверджувальних і загалшьнозапере-

чувальних суджень.

Книга перша. ТРАДИЦІЙНА ЛОГІКА

197

Наприклад, вираз «Деякі річки є судноплавними», його

перекладом мовою логіки предикатів буде вираз ∃х М(х),

якщо взяти за область значенняпредметної змінної мно-

жину річок. А якщо взяти за область значення – множи-

ну будь-яких об’єктів, то переклад цього судження матиме

вигляд

∃х (S(x) & P(x))

– читається: «Існує такий х, що має властивість S i

властивість Р».

S – це символ загального імені «річка». Фактично за-

гальне ім’я «річка» S виділяє в універсумі значень для х,

ті, яким може бути притаманна властивість «бути судно-

плавною».

Якщо наявна ситуація в), тобто коли мовою логіки пре-

дикатів перекладаються загальні судження, то користу-

ються формулою ∀х А(х). Наприклад, 1. «Будь-яка плане-

та є космічним об’єктом» –

∀х Р(х), або ∀х (S(x) ⊃ P(x)) –

(у випадку, коли областю значення х буде не «множина

планет», а множина будь-яких об’єктів).

2. «Жоден підозрюваний не має алібі» –

∀х К(х) або ∀х (S(x) ⊃ K(x)).

Таким чином, основними виразами логіки предикатів,

на які перекладаються атрибутивні судження, є такі:

1. «Київ є столичне місто» – а є Р = Р(а).

2. «Місяць не є планетою» – а не є Р =



Р (а).

3. «Будь-який квадрат – геометрична фігура» –

«Будь-який S є Р» = А = Asp = ∀x P(x) = ∀x (S(x) ⊃ P(x)).

4. «Жоден природний супутник не є планетою» –

«жоден S не є Р» = Е = Esp = ∀x P(x) = ∀x (S(x) ⊃P(x)).

5. «Деякі злочини є посадовими» –

І = Isp = ∃xP(x) = ∃x (S(x) & P(x)).

6. «Деякі злочини не є посадовими» –

О = Osp = ∃x



P(x) = ∃x(S(x) &



P(x)).

А. Є. Конверський. ЛОГІКА

198

Застосування знаку рівності (=) показує еволюцію фор-

малізації атрибутивних суджень, втілених у природній мо-

ві. Кожний вираз після знаку рівності фіксує відповідний

етап формалізації (наприклад, випадок 3: від першого,

напівформального: «Будь-який S є Р», аж до останнього:

∀х (S(x) ⊃ P(x)), що вже є виразом логіки предикатів.

Формули, які є перекладом атрибутивних суджень мо-

вою логіки предикатів, широко використовуються при по-

будові аналітичних таблиць для перевірки правильності

модусів простого категоричного силогізму.

6. Судження з відношеннями

Як уже зазначалося, у судженнях з відношеннями пре-

дикатом виступає така ознака, як «відношення».

Наприклад, «Арістотель – сучасник Платона». Із

цього слідує, що в цих судженнях предикат може відноси-

тися до пари, трійки, четвірки і т.д. предметів.

Судження з відношеннями за якістю поділяються на:

 стверджувальні і

 заперечувальні.

С т в е р д ж у в а л ь н и м називається таке су-

дження з відношеннями, в якому стверджується, що

предмети знаходяться у певному відношенні.

Наприклад, «Деякі міста більші столичних міст».

З а п е р е ч у в а л ь н и м називається таке су-

дження з відношеннями, в якому говориться про те, що

предмети не знаходяться у певному відношенні.

Наприклад: «Лейбніц не є ровесником Гегеля».

За кількістю судження з відношеннями поділяються на:

 одинично-одиничні;

 одинично-загальні;

 одинично-часткові;

 загально-загальні;

 загально-одиничні;

 загально-часткові;

 частково-часткові;

 частково-загальні;

 частково-одиничні.

Як і атрибутивні судження, судження з відношеннями

також можна перекласти мовою логіки предикатів.

Книга перша. ТРАДИЦІЙНА ЛОГІКА

199

Для того, щоб перекласти судження з відношен-

нями на мову логіки предикатів, необхідно виконати

такі дії:

1. Замінити одиничні імена предметними константами,

а загальні – предикатними константами.

2. Замінити кванторні слова відповідними кванторами.

3. Виписати квантори згідно того порядку, як вони вхо-

дять в дане судження.

4. Після послідовно виписаних кванторів записати пре-

дикат у якому індивідна змінна зв’язується першим по по-

рядку квантором.

Якщо це квантор загальності, то після даного пре-

дикату ставиться знак імплікації (⊃), а якщо квантор

існування, то – знак кон’юнкції (&); після знака імплі-

кації чи кон’юнкції ставиться ліва дужка, після якої

виписується предикат, у якому предметна змінна

зв’язується другим по черзі квантором.

5. Виписати формулу, що представляє останній пре-

дикат.

6. Після формули, яка представляє останній предикат

ставиться необхідна кількість правих дужок. Якщо су-

дження заперечувальне, то перед останнім предикатом ста-

виться заперечення.

Здійснимо переклад суджень з відношеннями мовою ло-

гіки предикатів:

«одинично-одиничне»

«Київ більший за Одесу» –

«а R в»;

«одинично-загальне»

«Мій брат знає всіх викладачів» –

∀x (Q(x) ⊃ R(a,x));

«одинично-часткове»

«Моя сестра вивчає деякі іноземні мови» –

∃x (P(x) & R(x,a));

«загально-одиничне»

«Всі студенти філософського факультету вивчають

логіку» –

∀x (S(x) ⊃ R(x,a));

А. Є. Конверський. ЛОГІКА

200

«загально-загальне»

«Будь-який нормативний курс з філософських дисцип-

лін більший будь-якого нормативного курсу з природничих

дисциплін» –

∀x ∀y (N (x) ⊃ (Q(y) ⊃ R(x,y));

«загально-часткове»

«Всі мої приятелі знають декого з моєї родини» –

∀x ∃y (P(x) ⊃ (Q(y) & R(x,y));

«частково-одиничне»

«Деякі викладачі знають мого брата» –

∃x (Q(x) & R(x,a));

«частково-часткове»

«Деякі мої приятелі вивчають деякі слов’янські мови» –

∃x ∃y (P(x) & (Q(y) & R(x,y));

«частково-загальне»

«Деякі словники більші будь-якого підручника» –

∃x ∀y (P(x) & (Q(y) ⊃ R(x,y)).

Знаючи суть процедури перекладу суджень з відношен-

нями на мову логіки предикатів можна здійснити цей пе-

реклад для будь-якого судження.

Наприклад, маємо судження «Всі студенти економіч-

ного факультету вивчають логіку, а деякі студенти еко-

номічного факультету вивчають географію» –

∀x (P(x) ⊃ R(x,a)) & ∃x (P(x) & R(x, в))

7. Судження існування

Наступний вид простих суджень – це «судження існу-

вання». У логіці їх ще називають «екзистенціальні су-

дження».

До суджень існування відносять судження, у яких

предикат представляє ознаку «бути існуючим».