Конверський А. Є. Логіка (традиційна та сучасна)

Подождите немного. Документ загружается.

Книга перша. ТРАДИЦІЙНА ЛОГІКА

221

Правило введення диз’юнкції (ВД):

∨∨

Приклад міркування, що відповідає правилу введення

диз’юнкції:

Дана форма мислення є поняттям.

ана форма мислення є поняття або с

дження.

Правила усунення диз’юнкції (УД):

AB,A ∨

Приклад міркування за правилом усунення диз’юнкції:

Він знає мого брата або мою сестру.

Він не знає мою сестру.

Отже, він знає мого брата.

Треба враховувати різницю смислів сполучника «або»:

1) сполучно-розділове «або»;

суворо розділове «або».

Нехтування цією різницею при вживанні диз’юнкції

призводить до логічної помилки. Наприклад,

Ця книжка належить моєму братові або моїй сестрі.

Ця книжка належить моєму братові.

Отже, ця книжка не належить моїй сестрі.

З’ясуємо логічну структуру цього міркування:

AB,A ∨

Якщо приєднати висновок до засновків через імпліка-

цію, то у результаті не отримаємо тотожно-істинної фор-

мули, а отже, висновок не відповідає визначенню правиль-

ного дедуктивного умовиводу.

а) [(А ∨ В) ∧ А] ⊃



В.

А. Є. Конверський. ЛОГІКА

222

У тих випадках, коли неможливо вирішити, в якому

смислі вживається сполучник «або», треба посилатися на

смисл сполучника «або» у сполучно-розділовому розумінні.

Розглянемо другий приклад.

Правила висновку логіки висловлювань бувають осно-

вні та похідні.

Це правило – основне.

Отже, це правило не похідне.

Логічна структура цього міркування має такий вигляд:

AB,A ∨

Отже, отримуємо

б) [(А ∨ В) ∧ А] ⊃



вираз, який на перший погляд еквівалентний виразу а).

Але це лише на перший погляд. Насправді тут присутній

ще один засновок, який вказує на те, що не існує правила,

яке одночасно було б і основним, і похідним (А ∧ В). З цим

засновком вираз б) стане тотожно-істинним:

в) [[(А ∨ В) ∧ А] ∧ (А ∧ В)] ⊃



В.

Виходить, наявність засновку А ∧ В свідчить про те, що

ми маємо сильну диз’юнкцію. Отже, вираз в) набуде ви-

гляду:

((А

∨ В) ∧ А) ⊃



В.

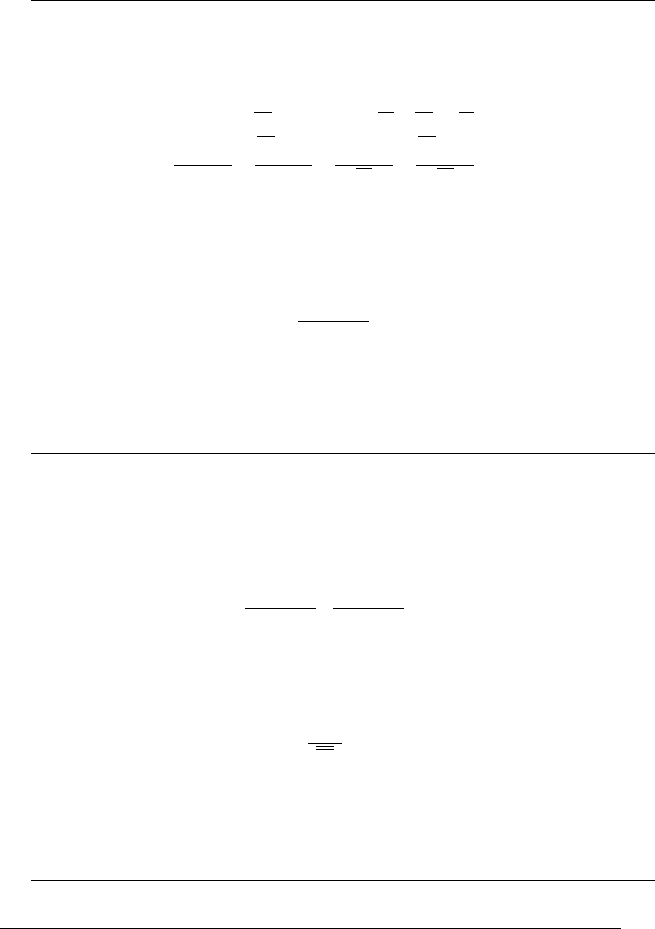
Правило усунення імплікації (УІ):

BA ⊃

Це правило ще називають відділенням висновку В від

засновку А ⊃ В за допомогою засновку А, а іноді назива-

ють правилом «ствердження за антецедентом».

Приклад міркування за правилом усунення імплікації:

Книга перша. ТРАДИЦІЙНА ЛОГІКА

223

Якщо поїзд запізнюється, то ми не встигаємо на ав-

тобус.

Поїзд запізнюється.

Отже, ми не встигаємо на автобус.

Правило УІ має такі різновиди:

BABABABA ⊃⊃⊃⊃

Правило введення еквіваленції (ВЕ):

↔

⊃

Приклад міркування за правилом введення еквіваленції:

Якщо на планеті є життя, тоді там є атмосфера.

Якщо на планеті є атмосфера, тоді там є життя.

Отже, на планеті є життя тоді і тільки тоді, коли

там є атмосфера.

Правило усунення еквіваленції (УЕ):

⊃

↔

⊃

↔

Правило введення подвійного заперечення (ВПЗ):

Приклад міркування за правилом введення подвійного

заперечення:

Ця книжка є підручником з логіки.

Отже, невірно, що ця книжка не підручник з логіки.

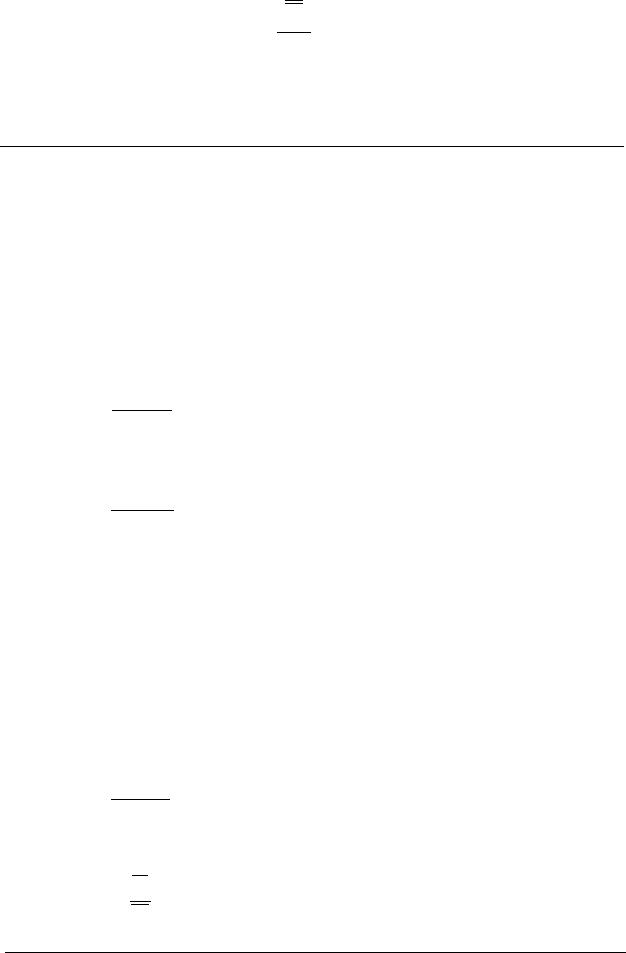
А. Є. Конверський. ЛОГІКА

224

Правило усунення подвійного заперечення (УПЗ):

Приклад міркування за правилом усунення подвійного

заперечення:

Невірно, що курсова робота не виконана самостійно.

Отже, курсова робота виконана самостійно.

Як уже зазначалося, окрім наведених основних правил

висновку логіки висловлювань існують і основні непрямі.

До них відносяться:

а) правило введення імплікації,

б) правило введення заперечення.

Правило введення імплікації (ВІ):

ВА

⊃

– (множина засновків)

– припущення

Це правило використовується у тих вивідних процесах,

коли для отримання висновку ми звертаємося до припу-

щень, які полегшують процедуру виведення. Його можна

сформулювати так: «Якщо із засновків П і з припущення

А випливає В, то можна стверджувати вивідність із

цих засновків А ⊃ В».

Правило введення заперечення (ВЗ):

– (множина засновків)

– припущення

Книга перша. ТРАДИЦІЙНА ЛОГІКА

225

Визначення цього правила таке: «Якщо із засновків і

довільного припущення А випливають два суперечливих

висловлювання В і



В, то таке припущення повинно

бути визнаним як хибне, істинним визнається



А».

Зупинимося на розгляді похідних правил висновку ло-

гіки висловлювань.

Правило транзитивності імплікації (ТІ) :

⊃

Приклад міркування за правилом транзитивності імплі-

кації:

Якщо мовний відрізок розповідне речення, то він є ви-

словлюванням.

Якщо мовний відрізок є висловлюванням, то він є

осмисленим.

Отже, якщо мовний відрізок розповідне речення, то

він є осмисленим.

б) Обгрунтування правил висновку

Для подальшого розгляду правил необхідно прийняти

деякі домовленості. Аналізуючи правила, природно вини-

кає питання, чи можна перевірити надійність цих правил,

їх коректність. На рівні семантики це можна зробити

шляхом побудови таблиць істинності, шляхом еквівален-

тиних перетворень, методом аналітичних таблиць (про що

буде сказано пізніше). На рівні синтаксису така перевірка

здійснюється через побудову доведення останнього рядка

правила.

Розглянемо на прикладі правила транзитивності імплі-

кації його семантичне та синтаксичне обгрунтування (на

предмет коректності).

Спочатку зупинимося на семантичному обгрунту-

ванні.

Побудова таблиць істинності, еквівалентні перетворення

(КНФ) досить громіздкі, тому можна запропонувати такий

спосіб.

А. Є. Конверський. ЛОГІКА

226

Відомо, що у правильному висновку між засновками і

висновком існує відношення логічного слідування, тобто

при істинності засновків висновок повинен бути обов’яз-

ково істинним. Виходячи з цього, в правилі ТІ між (А ⊃

В), (В ⊃ С) і (А ⊃ С) існує відношення логічного слідуван-

ня, отже, засновки (А ⊃ В) і (В ⊃ С) не можуть бути істин-

ними, а висновок (А ⊃ С) – хибним.

Припустимо, що це не так (тобто, що А ⊃ В і В ⊃ С –

істинні, а А ⊃ С – хибне).

Тоді А ⊃ С – хибне при умові А – і, С – х. А у засно-

вках: якщо А – і, а С – х, то при будь-якому значенні В

кон’юнкція засновків не буде істинною, а це суперечить

нашому припущенню.

Отже, засновки у нашому правилі не можуть бути іс-

тинними, а висновок – хибним, а це свідчить, що це пра-

вило логічно коректне і гарантує правильність відповідних

його структурі змістовних міркувань.

Схематично така перевірка коректності правила

висновку зображується таким чином:

}

xCA

xCB

ixi

xii

−⊃

⊃

З цієї схеми очевидно, що при будь-яких значеннях В

наше припущення про логічну некоректність правила від-

падає. У такий, можна сказати, досить економний спосіб

можна перевірити кожне з правил.

Синтаксичне обгрунтування правила висновку перед-

бачає побудову виведення останнього рядка із засновків.

Для цього розгорнемо правило, вставивши між заснов-

ками і висновком проміжні ланки, які в правилі опущені.

Доведення здійснюється таким способом:

1. Виписуємо засновки, що входять до правила.

2. Зліва виписуємо кроки доведення.

3. Справа напроти кожного кроку виписуємо його

підставу (це може бути домовленість про введення чер-

гового припущення, або певне правило). Праву сторону

такого запису називають аналізом доведення.

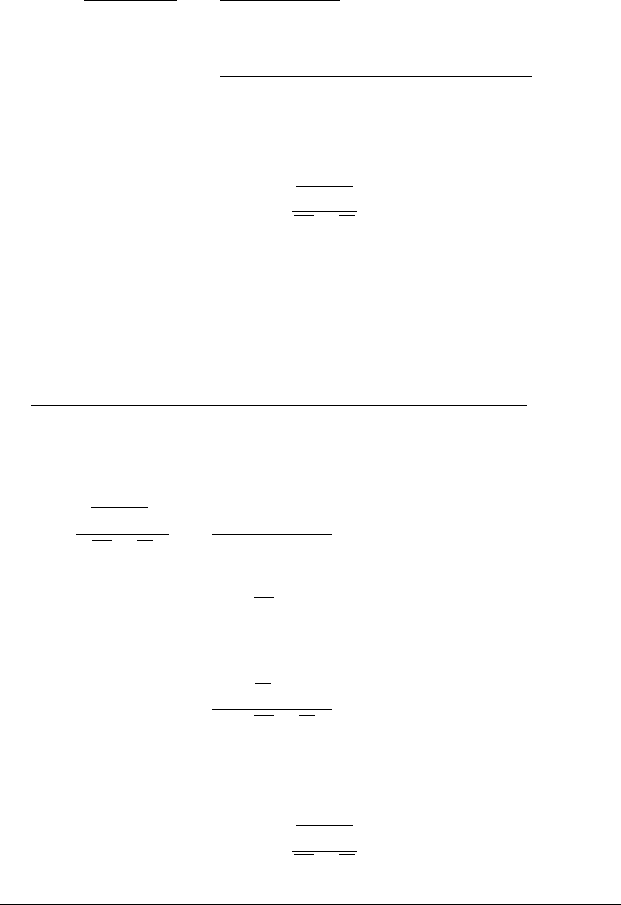
Книга перша. ТРАДИЦІЙНА ЛОГІКА

227

Здійснимо доведення правила ТІ:

BA ⊃

⊃

CB ⊃

2. C

⊃

засновки

CA ⊃

3. Априпущення

4. В – (УІ по 1, 3)

5. С – (УІ по 2, 4)

⊃

– (ВІ по 3, 5)

Правило заперечення диз’юнкції (ЗД):

∧

∨

Відповідно до цього правила із заперечення диз’юнк-

ції слідує кон’юнкція заперечень висловлювань, що її

складають.

Наведемо приклад міркування, побудованого за прави-

лом ЗД:

Неправильно, що він студент або школяр.

Отже, він і не студент, і не школяр.

Побудуємо доведення цього правила:

BA∨

⊃

BA ∧

2. А – (припущення 1)

∨

– (ВД по 2)

– (ВЗ по 1, 3)

5. В – (припущення 2)

∨

– (ВД по 5)

– (ВЗ по 2, 6)

∧

– (ВК по 4,7).

Правило заперечення кон’юнкції (ЗК):

∨

∧

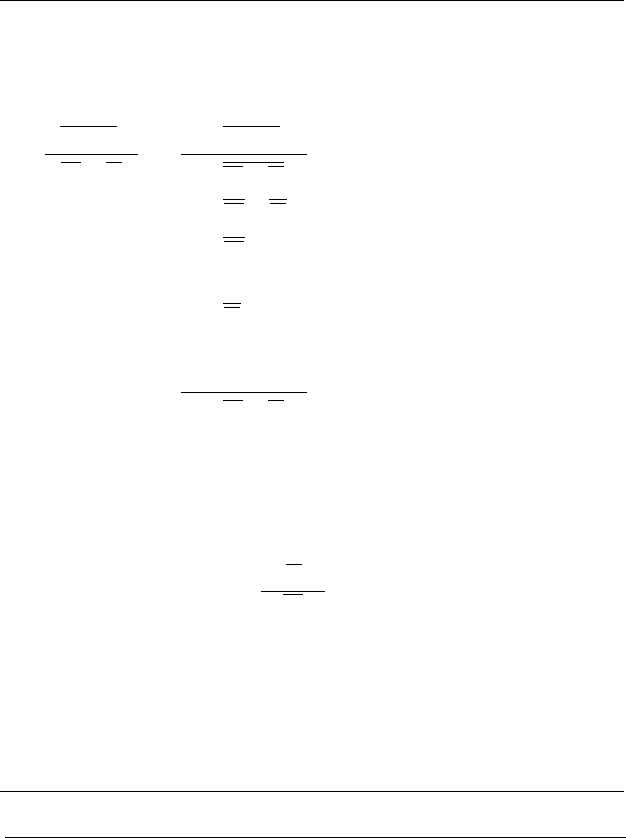
А. Є. Конверський. ЛОГІКА

228

Читається правило так: «Із заперечення кон’юнкції

слідує диз’юнкція заперечень висловлювань, що склада-

ють кон’юнкцію».

Наприклад:

Неправильно, що дане космічне тіло має ознаки пла-

нети і природного супутника.

Отже, дане космічне тіло або не має ознак планети,

або не має ознак природного супутника.

Доведення правила:

BA ∧ 1.

∧

BA ∨

∨

– (припущення)

∧

– (ЗД по 2)

– (УК по 3)

5. А – (УПЗ по 4)

– (УК по 3)

7. В – (УПЗ по 6)

∧

– (ВК по 5, 7)

∨

– (ВЗ по 1, 8).

Правило «modus tollens», або «від заперечення консеквенту

до заперечення антецеденту» (МТ):

⊃

Наведемо приклад конкретного міркування, що регла-

ментується цим правилом:

Якщо він знає англійськ

мов

, то він перекладе цей

текст.

Він не переклав цей текст.

Отже, він не знає англійської мови.

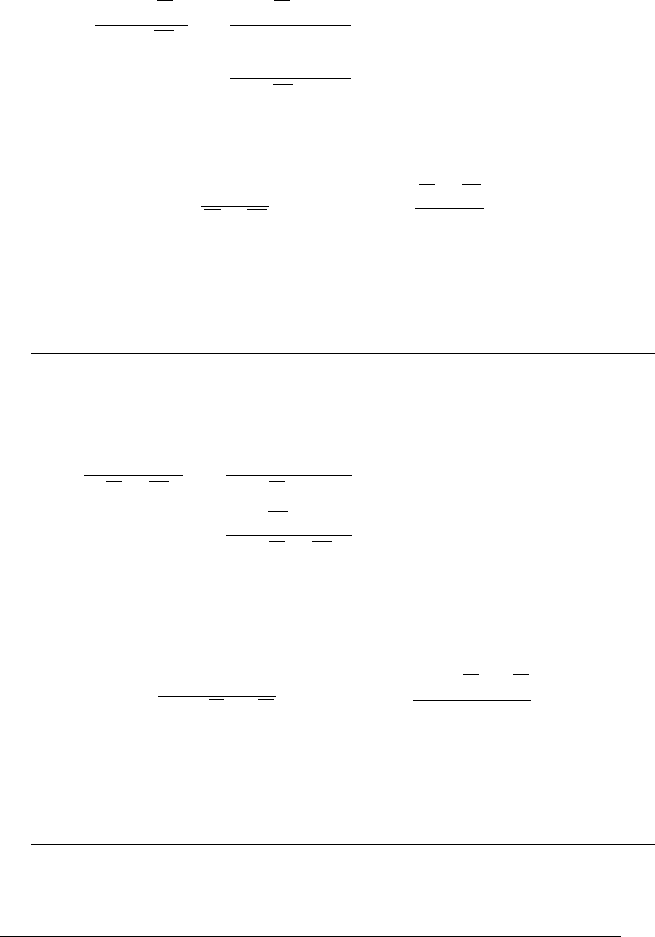
Книга перша. ТРАДИЦІЙНА ЛОГІКА

229

Доведення правила МТ:

BA ⊃

⊃

B 2.

3. А – припущення

4. В – (МП по 1, 3)

– (ВЗ по 2, 4).

Правило простої контрапозиції (ПК):

І.

⊃

І.

⊃

Наведемо приклад міркування, побудованого за прави-

лом простої контрапозиції:

Якщо лист написаний мною, то його зміст повинен

бути мені відомим.

Отже, якщо мені невідомий зміст листа, то він на-

писаний не мною.

Побудуємо доведення цього правила:

BA ⊃

⊃

AB ⊃ 2.

– (припущення)

– (МТ по 1, 3)

⊃

– (ВІ по 2, 3)

(аналогічно доводиться і друге правило ПК).

Правило складної контрапозиції (ПСК):

І.

()

BCA

CBA

⊃∧

І.

()

CBA

BCA

⊃∧

Наведемо приклад конкретного міркування за правилом

складної контрапозиції:

Якщо іспит з історії є першимі і він профілюючий, то

він є вирішальним для абітурієнта-медаліста.

Отже, якщо іспит з історії є першим, але він не ви-

рішальний для абітурієнта-медаліста, то він не про-

філюючий.

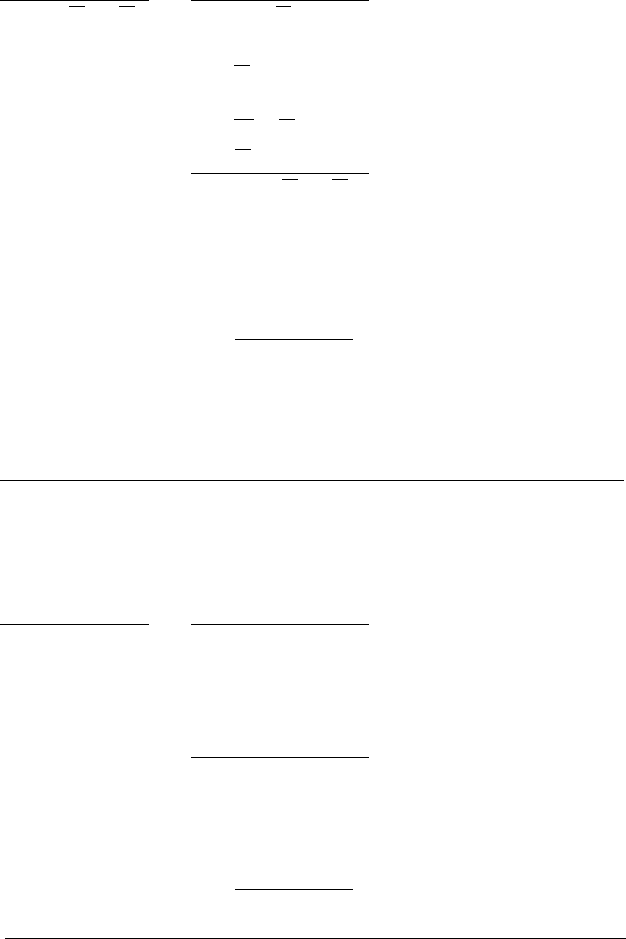
А. Є. Конверський. ЛОГІКА

230

Побудуємо доведення цього правила:

()

CBA ⊃∧ 1.

()

CBA ⊃∧

()

BCA ⊃∧

2. C

∧

– (припущення)

3. А – (УК по 2)

– (УК по 2)

∧

– (МТ по 1, 4)

∨

– (ЗК по 5)

– (УД по 3, 6)

()

BCA ⊃∧

– (ВІ по 2,7)

(аналогічно будується доведення правила ІІ).

Правило імпортації (ПІмп):

()

CBA

⊃∧

⊃⊃

Наведемо приклад міркування за цим правилом:

Якщо він добре знає англійськ

мов

, то

випадк

якщо приїде англійська делегація, він зможе виконати

роль перекладача.

Отже, якщо він добре знає англійськ

мов

і приїде

англійська делегація, то він зможе виконати роль пе-

рекладача.

Побудуємо доведення цього правила:

()

CBA ⊃⊃ 1.

()

CBA ⊃⊃

()

CBA ⊃∧

∧

– (припущення)

3. А – (УК по 2)

4. В – (УК по 2)

⊃

– (МП по 1, 3)

6. С – (МП по 4, 5)

()

CBA ⊃∧

– (ВІ по 2, 6).

Правило експортації (ПЕкс):

()

CBA

⊃⊃

⊃∧