Кузьмин С.И. Методы научных исследований в технических задачах
Подождите немного. Документ загружается.

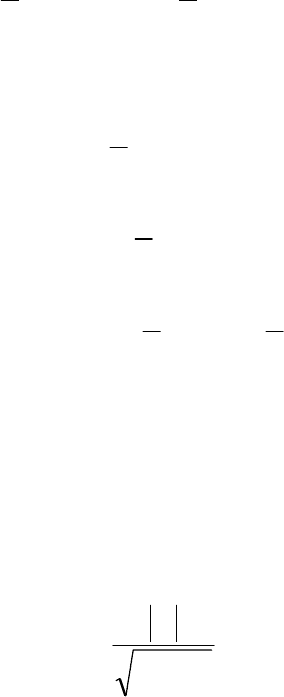
101
циенты при различных факторах вычисляются по формулам
[7]:
)(
1
2
11
0
∑∑∑
===
−=
N
u
iuuoi
K
i
N
u
uo
XYAYАb
(6.7)
22
}{
Yoo
SAbS =
;)(
1
∑
=
=
N
u
uiuii
YxАb
22
}{
Yii
SAbS =
;)(
1
u
N
u
ujiijij
YxxАb
∑
=
=
22
}{
Yijij
SAbS =
;
11
2
∑∑
==
−=
N
u
uoi
N
u
uiiiii
YAYxАb
22
}{
Yiiii
SAbS =
Рассчитанные по формулам коэффициенты
i
b
, уравне-
ний проверяют на статистическую значимость по критерию
Стьюдента
i
t
:
}{
2
i
i
i
bS
b
t =
,
где
}{
2
i
bS
- дисперсия оценки коэффициента.
Если
табл
fi
y
tt
);(
α
<
, то гипотеза о значимости коэффициента
отвергается с уровнем значимости
α
и коэффициент прирав-
нивается к нулю. Табличное значение критерия Стьюдента в
технико-экономических задачах обычно определяется для
уровня значимости равного 0,05 или 0,1.
Удаление статистически незначимого коэффициента из
уравнения модели показывает, что фактор (сочетание факто-
ров), при котором он находился, не влияет на поведение сис-
темы. Однако необходимо иметь в виду, что
на степень влия-
ния фактора на выходной параметр сказывается не только его
действительная значимость, но и выбранные пределы варьи-
рования. Если интервал изменения
i
x
, не велик, то скорее

102
именно это является причиной нечувствительности иссле-
дуемой системы к данному фактору. Поэтому утверждение
об отсутствии влияния фактора на параметр оптимизации от-
носят только к рассматриваемой области исследования.
Незначимый коэффициент, исключается из уравнения
без каких-либо последствий для других коэффициентов толь-
ко в ортогональных планах. Если план не обладает этим
свойством, то
при исключении какого-либо коэффициента,
необходимо пересчитывать значения оставшихся коэффици-
ентов.
После исключения незначимых коэффициентов из урав-
нения (6.5) необходимо убедиться насколько правильно и
точно оно описывает поведение целевой функции в базовых
точках факторного пространства. Эта процедура называется
проверкой адекватности уравнения регрессии и проводится
путем сравнения дисперсии
2
ад
S
характеризующей точность
совпадения средних результатов опытов
u
y
с предсказанны-
ми по уравнению результатами
n
y
при одинаковых значениях
аргументов и дисперсией воспроизводимости опытов
2
y
S
:
()
lN
yyM
S
N
n
n
ад
−
−
=
∑
−1
2
2
€
,
где
l
- число значимых коэффициентов в уравнении.
Проверку однородности двух дисперсий осуществляют
сравнением критериев Фишера - расчетного
p
F
и табличного
()
над
ffТ
F
.
;
α
.
≤=
2
2
y
ад
p
S
S
F
()
над
ffТ
F
.
;
α
,
lNf
ад
−=
;
)1(
−
=
mNf
y
(6.8)
Если условие (6.8) подтверждается, то гипотеза об адек-
ватности уравнения регрессии принимается с уровнем значи-
103
мости
α
, который в свою очередь назначается исходя из ус-
ловий решаемой задачи.
Если условие (6.8) не выполняется, то теория дисперси-
онного анализа не рекомендует использование полученной
модели для анализа поведения объекта.
Однако следует помнить, что неадекватность уравнения
регрессии оценивается чисто математическими приемами, и
при решении технико-экономических задач полезно проана-
лизировать полученный
результат на предмет величины
ошибки модели, ее поведения в факторном пространстве.
Возможно несколько вариантов принятия решения.
Неадекватность уравнения может быть следствием не
только (и не столько) большой его ошибки, но и завышенной
точности эксперимента. При хорошей воспроизводимости
процесса и высокоточных приборах, дисперсия опытов ока-
зывается малой и формальная проверка адекватности
по (6.8)
практически никогда не выполняется. С другой стороны в
технических задачах считается приемлемой погрешность по-
рядка 10%, а в некоторых случаях и 20%. Поэтому, если дис-
персия адекватности удовлетворяет исследователя, то можно
рекомендовать прием увеличения дисперсии воспроизводи-
мости до некоторой условной величины
2
yу
S
, обеспечиваю-
щей выполнение проверки (6.6.).
Этого же можно добиться и за счет снижения довери-
тельной вероятности
)1(
α
−
=
p
, если такое решение не про-
тиворечит условиям задачи (к стати сказать, выбор конкрет-
ного уровня доверительной вероятности при вычислении
критерия Фишера остается операцией наименее поддающей-
ся формализации и полностью возлагается на исследователя).
Здесь может иметь место и обратная задача - определение
такой величины доверительной вероятности, при которой
модель процесса становится адекватной
эксперименту.
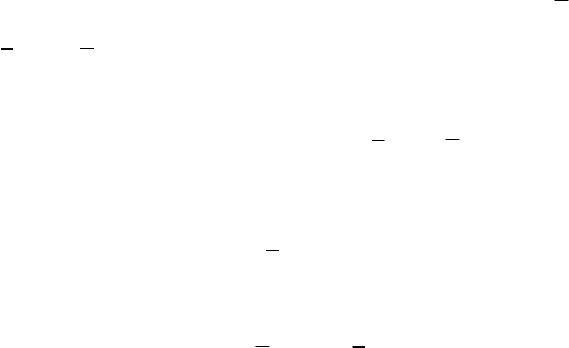
104
Повышению точности модели может значительно спо-
собствовать и количество членов в уравнении (6.5.). Как по-
казывает опыт, исключение коэффициентов, по условию не
всегда целесообразно, так как несколько даже незначитель-
ных коэффициентов могут в сумме внести решающий вклад
в снижение дисперсии адекватности. С этой же целью можно
рекомендовать рассчитывать коэффициенты при всех эффек
-
тах взаимодействия. Конечно, это усложняет модель, но со-
временная техника позволяет не только решить проблему
вычислений, но и исследования поведения и оптимизации
модели без значительных затрат времени.
Иногда для достижения адекватности бывает полезным
преобразование выходного параметра
y
в иную функцию
)( yfz =
и строить модель для нее. Чаще других для этих це-
лей используется логарифмирование:
yz ln
=
Модель процесса будет выглядеть как:
iizz
z
o
xbxbbz
+
+
+
= ...
11
и соответственно переход к начальному уравнению:
)...exp(exp
1 izit
bxbzy
+
+
=
=
Кроме математических приемов, для устранения неадек-
ватности модели, можно сформулировать и методические ре-
комендации. Во-первых - полезно пересмотреть интервал
варьирования факторов
i
X
Δ
,. Как правило, уменьшение
i
XΔ
,
ведет к большей сходимости модели. Во-вторых - попытаться
применить другие планы для реализации эксперимента. На-
пример, перейти от линейной или неполной квадратичной
модели к квадратичной. Ниже рассматриваются принципы
использования наиболее часто применяемых на практике
планов и приводятся комментарии по их использованию в
технических исследованиях. Более подробные сведения о

105
планах и их характеристиках можно найти в специальной ли-
тературе [10].
6.3 Характеристика планов многофакторных
исследований
6.3.1 Полный факторный эксперимент (ПФЭ)
План исследований, в котором реализуются все возмож-
ные (требуемые) сочетания уровней факторов, называется
полным факторным экспериментом. Количество опытов
N
в
этом плане составляет:
k
nN =
где
n
- число уровней варьирования факторов;
k
- число
факторов.
Если эксперименты проводятся по плану ПФЭ только на
двух уровнях варьирования значений аргументов, то такой
план называется полным факторным экспериментом типа
k
2
,
если на трех уровнях, то ПФЭ типа
k
3
и т.п. Наибольшее рас-
пространение получили планы ПФЭ типа
k
2
, т.к. позволяют
получить линейные и неполные квадратичные модели с ми-
нимальными затратами ресурсов.
Принцип построения плана ПФЭ иллюстрирует матрица
плана для трех входных факторов приведенная в таблице 6.6,
где верхний уровень варьирования обозначается как «+ 1»
(или чаще просто «1»), нижний «-1» (или просто «-»).
Собственно план проведения опытов составляют гра-
фы 2, 3, 4 с информацией
о значениях аргументов
()
j
i
x
в
каждом опыте в кодовой системе координат:
i
ioi
i
X
XX
x
Δ
−
=
;
2
∨∧
−
=Δ
ii
i
XX
X
;
2
∨∧
+
=
ii
io
XX
x
где
i
x
- значение
i
-го аргумента в кодовой системе;

106
0
,,
iii
XXX
∨∧
значение
i
-го аргумента в натуральной системе,
соответственно на верхнем, нижнем, и основном уровнях
варьирования.
Таблица 6.6
План ПФЭ типа 2
3
Матрица плана
№
опыта
j
1
x (a)
2
x (в)
3
x (с)
Фиктивная
переменная
0
x
Условная запись комби-
нации значений аргумен-
тов в опыте
Выход
j
y
1 +1 +1 +1 +1
Abс
1
y
2 -1 +1 +1 +1
Bс
2
y
3 +1 -1 +1 +1
Ac
3
y
4 -1 -1 +1 +1
C
4
y
5 +1 +1 -1 +1
Ab
5
y
6 -1 +1 -1 +1
B
6
y
7 +1 -1 -1 +1
A
7
y
8 -1 -1 -1 +1
(1)
1
y
Для первого фактора его значения чередуются на приня-
тых уровнях от опыта к опыту. И далее для каждого после-
дующего фактора интенсивность чередования уменьшается
удваиванием по отношению к предыдущему столбцу. Графа
5 вводится для удобства расчетов и называется фиктивной
переменной
0
x
, в графе 7 приводятся обработанные значения
целевой функции
Y
.
Кроме табличной формы, матрицу плана ПФЭ 2
к
иногда (с
целью сокращения записи) представляют в условном виде
(графа 6): - верхний уровень факторов
i
xxx ,...,
21
, обозначают
буквами а, b, с,...f, нижний уровень не обозначается и опыт, в
котором все факторы равны (-1) записывают как (1). Тогда
план 2
3
в условном виде запишется следующим образом:
(аbс, bс, ас, с, аb, b, а, (1)). Аналогично можно записать лю-
бой другой план типа
k
2
.
План типа 2
3
геометрически можно интерпретировать в
виде куба, восемь вершин которого представляют восемь
экспериментальных точек, а плоскости сторон - границы об-
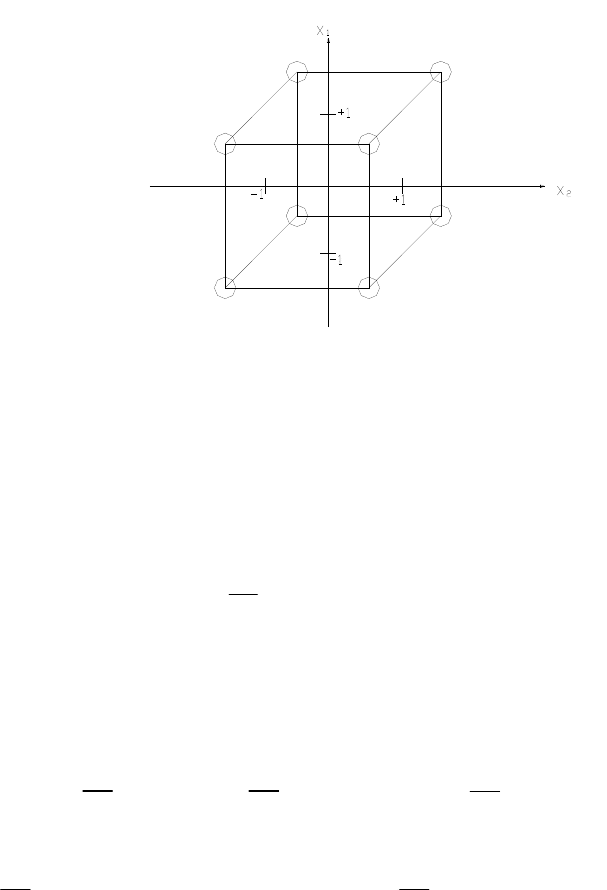
107
ласти исследования (рис. 6.2). При
k
>3 областью экспери-
мента является гиперкуб с опытами в его вершинах.
Рис. 6.2. Область исследования в ПФЭ типа 2
3
Полный факторный эксперимент типа
k
2
обладает свой-
ствами ортогональности и рототабельности. Вычисление ко-
эффициентов в уравнении регрессии ведется по формуле:
∑
=
=
N
p
jiji
yx
N
b
1
1
(6.9)
или соответственно для коэффициентов:
∑∑
==
==
N
j
N
j
jj
y
N
yx
N
b
11
00
11
∑
=
=
N
k
jkjijik
yxx
N
b
1
1
;
∑
=
=
N
j
jkjsjijisk
yxxx
N
b
1
1
;
∑
=
=
N
j
jiji
yx
N
b
1
1
(6.10)
Для вычисления коэффициентов при эффектах взаимо-
действия (
ik
x
,
ks
x
,
is
x
,
iks
x
) вводят дополнительные столбцы
в таблицу 6.6, получая расширенную матрицу плана (таблица
6.7).
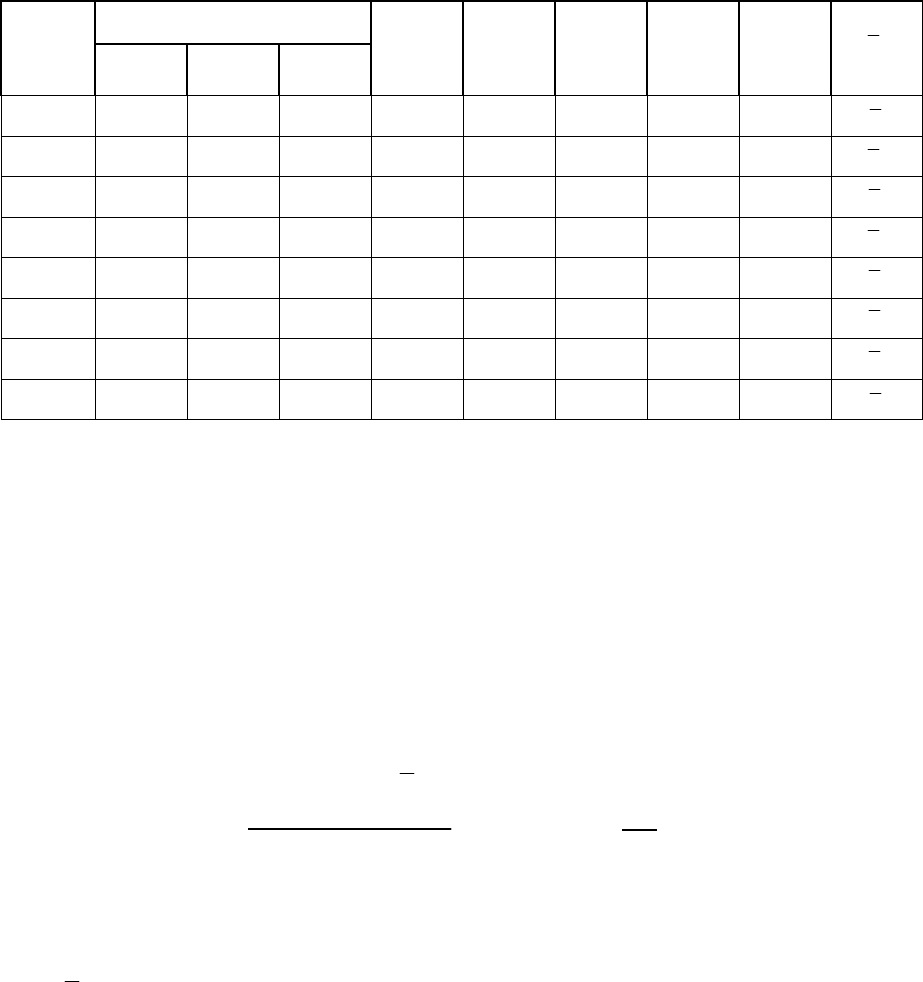
108
Таблица 6.7.
Расширенная матрица плана ПФЭ 2
3
Матрица плана
№
опыта
1
x
2
x
3
x
0
x
21
xx
31
xx
32
xx
321
xxx
j
y
1 + +
+ +
+
+
+
+
1
y
2
-
+ +
+
- - + -
2
y
3 + -
+ +
- + -
-
3
y
4
-
-
+
+ + - - +
4
y
5 + +
-
+ + - - -
5
y
6
-
+ - +
-
+ - +
6
y
7 + - - + - - + +
7
y
8 - - - + + + + -
1
y
Значение «аргумента» в столбце получается перемно-
жением соответствующих столбцов матрицы плана.
Значимость коэффициентов проверяется по критерию
Стьюдента -
i
t
, Дисперсию оценок коэффициентов
}{
2
i
bS
=
2
bi
S
одинаковую для всех коэффициентов определяют
по дисперсии воспроизводимости
2
y
S
:
)1(
)(
11
2
2
−
−
=
∑∑
==
mN
yy
S
N
j
m
h
jhj
y
и
N
S
S
y
bi
2
2
=
,
где
m
- число параллельных опытов (реализованных при по-
стоянном значении аргументов – входных факторов);
j
y
- среднее значение выходного параметра в серии из
m
повторений в
j
-м опыте.
Число степеней свободы критерия Стьюдента равно:
)1(
−
=
mNf
y
Критическое значение коэффициентов в уравнении регрессии
iкр
b
.
:
()
bifiкр
Stb
y
*
;.
α
=

109
Коэффициент считается значимым, если его значение по
абсолютной величине больше
iкр
b
.
:
kpii
bb ≥
. (6.11)
Так как план ПФЭ
k
2
обладает свойством ортогонально-
сти, то незначимые коэффициенты можно приравнивать к
нулю без пересчета оставшихся коэффициентов.
Адекватность исправленной «модели» процесса (после
удаления из уравнения незначимых коэффициентов) прове-
ряется из сравнения двух дисперсий – адекватности
2
ад
S
и
воспроизводимости
2
y
S
- по критерию Фишера
F
:
2
2
y
ад
S
S
F =
;
lN
yy
S
N
j
j
ад
−
−
=
∑
=1
2
2
)
€
(
, (6.12)
где
l
- число значимых коэффициентов в «исправленном»
уравнении регрессии;
j
y
€
- значение выходного параметра вычисленного по
«исправленному» уравнению в каждом опыте.
Пример. Необходимо выявить зависимость плотности
строительного материала, созданного на основе каустическо-
го магнезита (вяжущее вещество) и древесных отходов в виде
опилок. Получение материала заключается в смешении раз-
личных количественных соотношений твердых составляю-
щих и затворении полученной смеси определенным количе-
ством водного раствора хлористого магния. Полученный ма-
териал по плотности занимает промежуточное
положение
между чистой древесиной (плотность сосны примерно 500
кг/м
3
) и искусственным камнем (плотность бетона около
2500 кг/м
3
).

110
Формализация исследований
Целевая функция - плотность композиционного мате-
риала
ρ
- масса в единице объема материала (см. табл.1).
Факторы, влияющие на плотность: - соотношение меж-
ду массовыми частями составных компонентов материала:
вяжущего и древесного заполнителя, вяжущего и затворителя
(раствора хлористого магния), плотность водного раствора
хлористого магния (см. табл.2).
Методика определения плотности заключается в изго-
товлении образцов материала в виде прямоугольного пара-
леллепипеда
стандартного размера, измерения и вычисления
его истинного объема
V
, определения массы образца путем
взвешивания на весах и расчета плотности по формуле:
V
m
⋅
=
1000
ρ
, [кг/см
3
]
где т - масса образца, кг;
V
- объем образца, м
3
.
Прямые измерения проводились следующими приборами:
штангенциркуль (погрешность - 0,1мм), весы (погрешность – 1 г.)
Таблица 1
Характеристика целевой функции
Пределы существования
Наименование
Ед.
Изм.
Обозначение
Физические Желаемые
Плотность кг\м
3
ρ
10 – 13500
600 – 1300
