Кузьмин С.И. Методы научных исследований в технических задачах

Подождите немного. Документ загружается.

131

С учетом выводов табл. 3 уравнение характеристики

профильной пластины примет вид:

2321323121321

5,15,3145,55,3207,14621 xxxxxxxxxxxxx +−+−−++−=

Проверка адекватности уравнения эксперименту выпол-

нена по критерию Фишера -

Дисперсия адекватности

ад

S равна:

16,1

81,5

ад

Расчетное значение критерия

77,0

5,1

16,1

==F

а табличное

9,2

)14;5;05,0(

ТАБЛ

Следовательно, полученное уравнение, адекватно экспе-

рименту и его можно применять для разработки методики

конструирования приточных устройств.

6.4.3 Несимметричные планы типа М

⋅М

В технических задачах возникают ситуации, в которых

невозможно или не желательно выполнять условия одинако-

вого числа уровней вариации для всех входных факторов.

Так, например, может возникнуть необходимость в уменьше-

нии шага изменения только одного из факторов, для уточне-

ния поведения модели или увеличения её степени по этому

аргументу. В этом случае

можно применять планы, разо-

бранные в [9], в которых число уровней

для различных

факторов не одинаково. Коэффициенты

в уравнении рег-

рессии вычисляются по формулам (6.7). Расчетные коэффи-

циенты

для двух- и трехфакторных планов приведены в

таблицах 6.16 и 6.17.

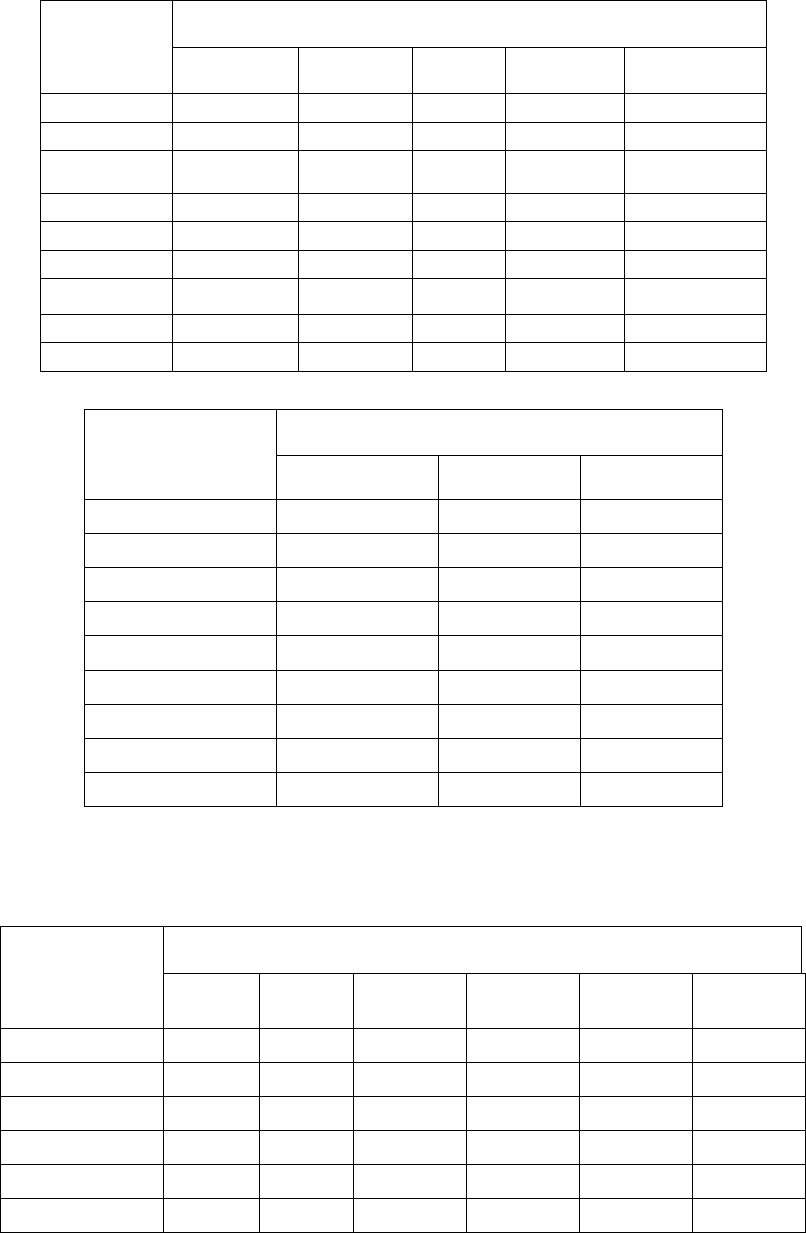
132

Таблица 6.16

Значение постоянных

для

коэффициентов регрессии двухфакторных планов

Коэффициенты

⋅10

План

хMM

2х3 50000 0 50000 16667 25000

2х4 32031 0 35156 12500 25500

2х5 24286 0 28576 10000 20000

2х6 19727 0 24414 8333 17852

3х4 38021 25000 23438 12500 15000

3х5 29524 20000 19048 10000 13333

3х6 24262 16667 16276 8333 11905

4х5 19955 14062 14286 9000 10000

4х6 12653 9524 4766 6667 7143

Продолжение табл.6.16

Коэффициенты

⋅10

План

хMM

2х3 0 25000 25000

2х4 0 62281 22500

2х5 0 57148 20000

2х6 0 52316 17857

3х4 37500 42188 22500

3х5 30000 38095 20000

3х6 25000 34877 17852

4х5 25312 28571 18000

4х6 19048 20926 14286

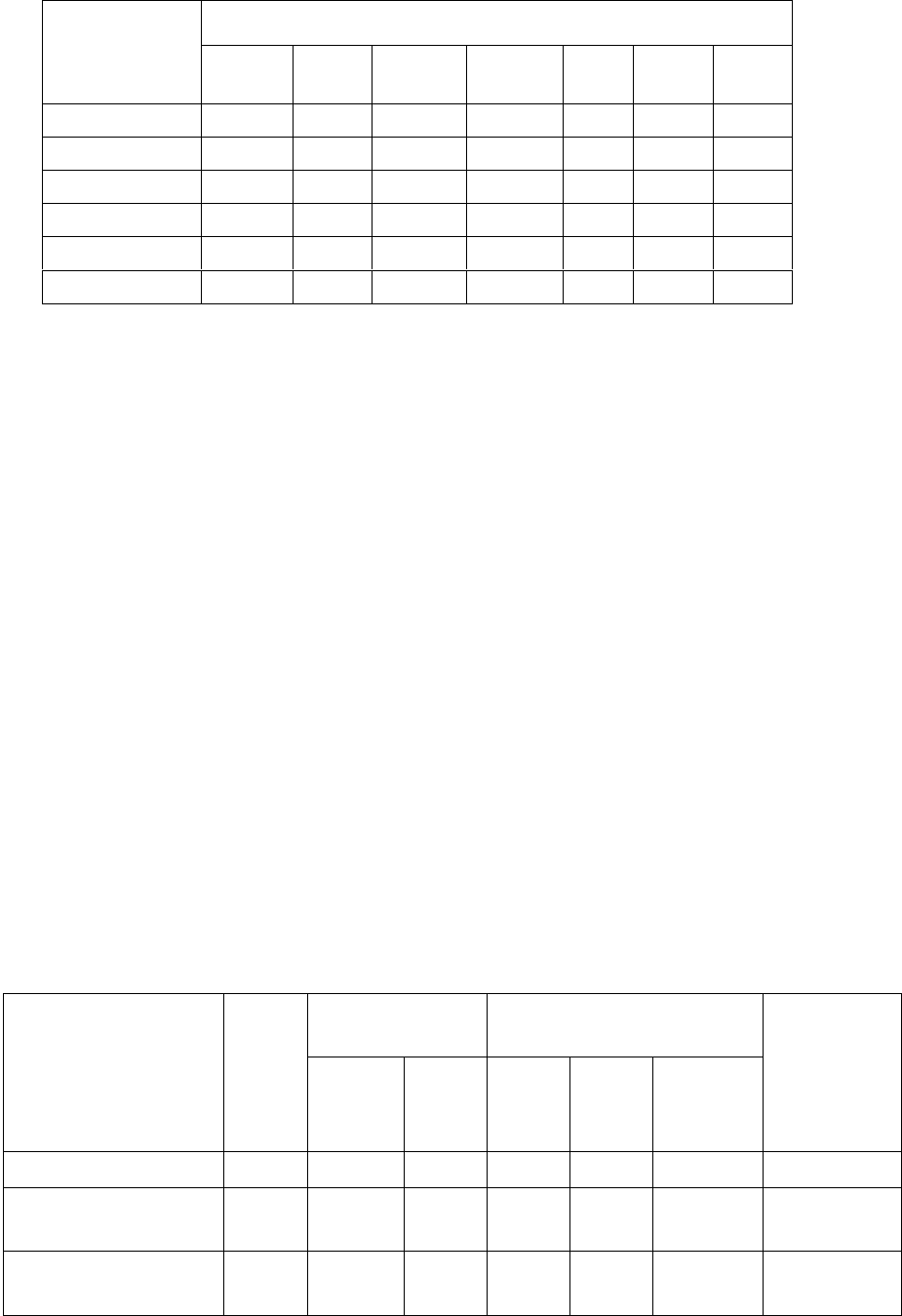
Таблица 6.17

Значение постоянных

для

коэффициентов регрессии трехфакторных планов

Коэффициенты

⋅10

План

321

хMхMM

2х2х3 25000 0 0 25000 833 8333

2х2х4 16016 0 0 17578 6250 6250

2х3х3 27778 0 16677 16667 5556 8333

2х3х5 14762 0 10000 9524 3333 5000

2х4х5 9978 0 7031 7143 2500 4500

3х3х5 14286 6667 3667 6349 3333 3333

133

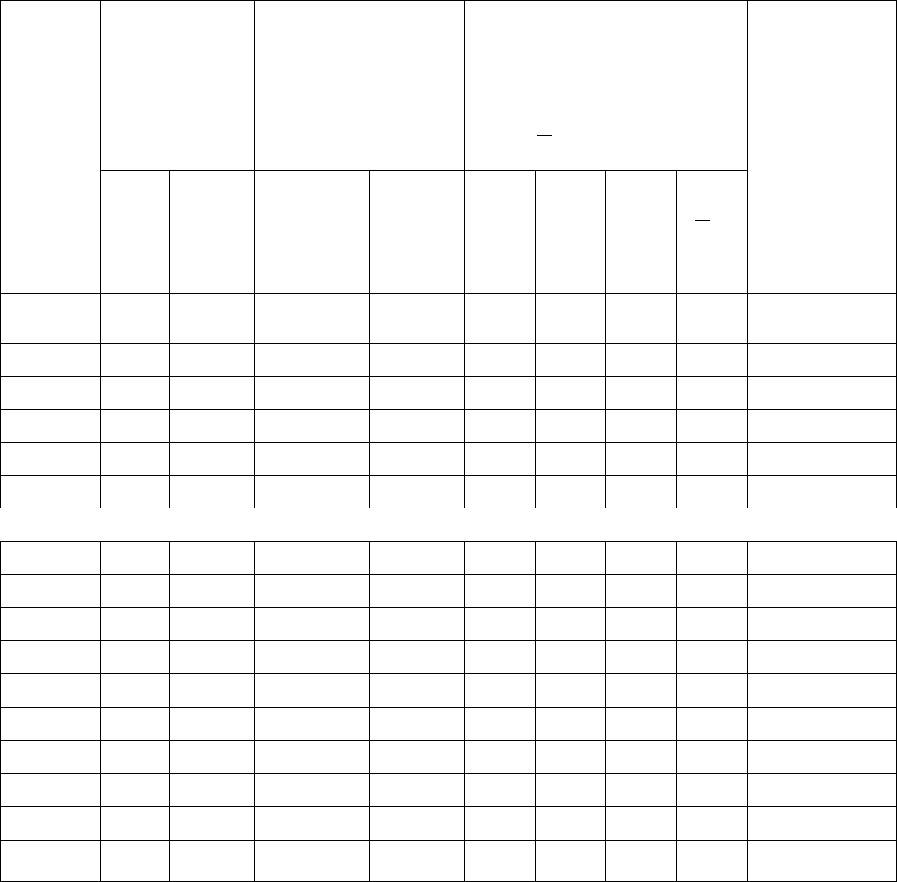
Продолжение таблицы 6.17

Пример. Строительный материал, полученный на основе

магнезиального вяжущего и древесных заполнителей (опи-

лок) набирает прочность во времени в зависимости от кон-

центрации затворителя – водного раствора хлористого маг-

ния -

MgCl

. Для разработки технологической карты произ-

водства изделий из данного материала необходимо иметь

формульную зависимость динамики набора прочности.

Прочность материала соответствует сопротивлению

стандартных образцов на сжатие

сж

[

/ cмкг

]. Характери-

стика входных факторов приведена в таблице 1. Концентра-

ция хлористого магния в растворе затворителя оценивается

по плотности водного раствора

MgCl

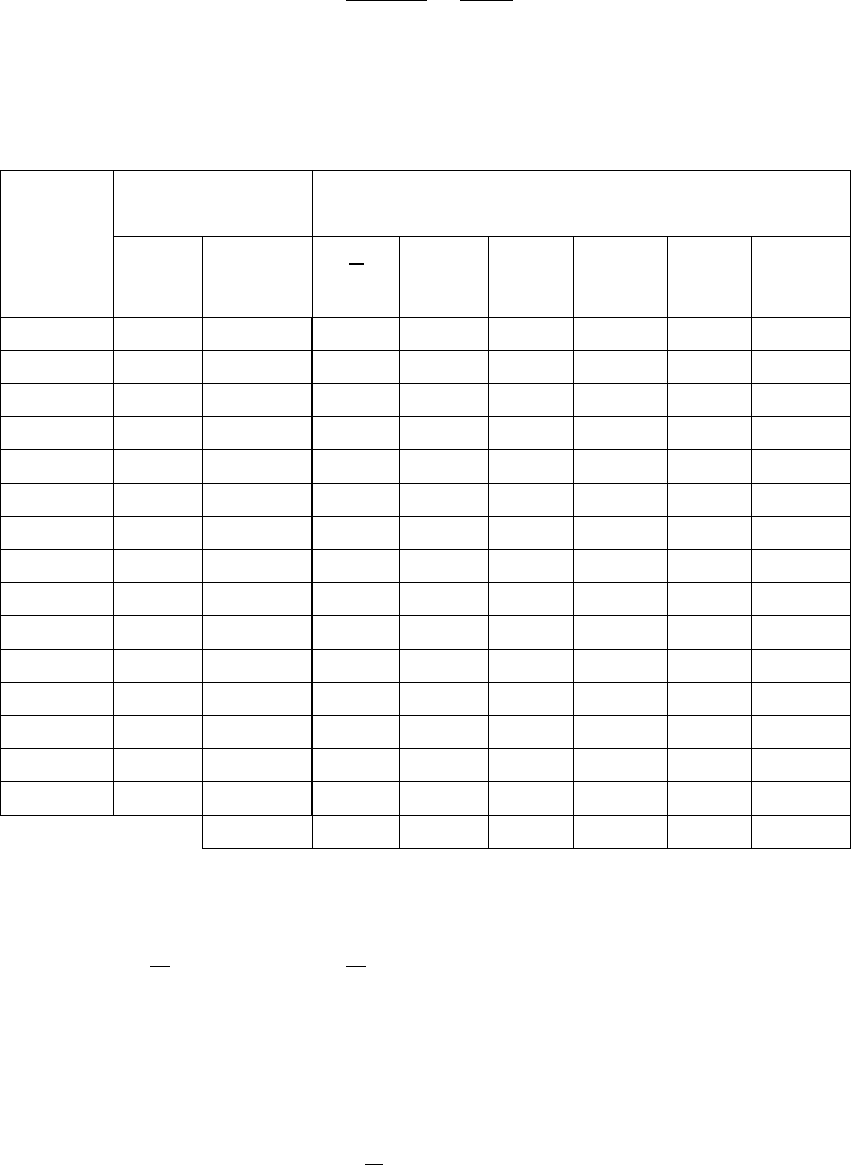
Таблица 1

Характеристика входных факторов в исследовании

динамики набора прочности строительного

материала

Обозначение в

координатах

Уровни

Наименование

Ед.

изм.

Нату-

раль-

ных

Кодо-

вых

ниж-

ний

Основ

ной

Верх-

ний

Интервал

варьиро-

вания

1 2 3 4 5 6 7 8

Плотность затво-

рителя

/ мкг

MgCl

1,05 1,125 1,2 0,075

Срок набора

прочности

Сутки

1 15 29 14

Коэффициенты

⋅10

План

321

хMхMM

2х2х3 12500 0 0 37500 8333 12500 12500

2х2х4 11250 0 0 31641 6250 11250 11250

2х3х3 81333 0 25000 25000 8333 8333 12500

2х3х5 6667 0 15000 19048 5000 6667 10000

2х4х5 5000 0 12656 14286 4500 5000 9000

3х3х5 4444 10000 10000 12698 5000 6667 6667

134

В следствие явной нелинейности набора прочности мате-

риала во времени в качестве плана эксперимента принят не-

симметричный план 3х5 с испытанием образцов в пяти кон-

трольных сроках: 1, 8, 15, 22 и 29 сутках.

Модель процесса находится в виде квадратичного двух-

факторного полинома:

222

1121122211

хbхbххbхbхbbу

+++++=

. (1)

План проведения опытов и результаты испытаний приве-

дены в таблице 2.

Таблица

Результаты эксперимента для модели 3*5

Матрица

плана

Значение фак-

тора в опыте

Значение выходного

параметра

сж

опыте

и среднее

/ cмкг

№

Опыта

MgCl

/ мкг

Сутки

2 u

Дисперсия

опыта

уu

1 -1 -1 1,05 1

2,2 2,3 2,1 2,2

0,01

2 0 -1 1,125 1 9,0 11,7 9,6 10,1 2,010

3 +1 -1 1,2 1 26,9 25,7 27,5 26,7 0,840

4 -1 -0,5 1,05 8 7,1 5,9 7,1 6,7 0,480

5 0 -0,5 1,125 8 19,6 22,3 22,9 21,6 3,090

6 +1 -0,5 1,2 8 46,3 45,9 48,2 46,8 1,510

Продолжение таблицы 2

7 -1 0 1,05 15 13,2 13,3 11,6 12,7 0,910

8 0 0 1,125 15 34,3 32,8 30,7 32,6 3,270

9 +1 0 1,2 15 65,5 66,7 64,6 65,6 1,110

10 -1 +0,5 1,05 22 18,6 19,4 18,7 18,9 0,190

11 0 +0,5 1,125 22 43,2 44,3 48,4 45,3 7,510

12 +1 +0,5 1,2 22 67,9 69,5 75,9 71,1 17,920

13 -1 +1 1,05 29 25,9 21,6 23,6 23,7 4,630

14 0 +1 1,125 29 47,3 50,5 52,8 50,2 7,630

15 +1 +1 1,2 29 71,5 72,8 71,1 71,8 0,790

∑

51,9

135

Дисперсия воспроизводимости определится как средняя по

всем опытам:

46,3

9,51

∑

Расчетная матрица плана для определения коэффициен-

тов модели представлена в таблице 3.

Таблица 3

Матрица

плана Расчетная матрица

№

Опыта

xyx

1 -1 -1 2,2 -2,2 -2,2 2,2 2,2 2,2

2 0 -1 10,1 0 -10,1 0 0 10,1

3 1 -1 26,7 26,7 -26,7 -26,7 26,7 26,7

4 -1 -0,5 6,7 -6,7 -3,35 3,35 6,7 1,675

5 0 -0,5 21,6 0 -10,8 0 0 5,4

6 1 -0,5 46,8 46,8 -23,4 -23,4 46,8 11,7

7 -1 0 12,7 -12,7 0 0 12,7 0

8 0 0 32,6 0 0 0 0 0

9 1 0 65,6 65,6 0 0 65,6 0

10 -1 0,5 18,9 -18,9 9,45 -9,45 18,9 4,725

11 0 0,5 45,3 0 22,65 0 0 11,325

12 1 0,5 71,1 71,1 35,55 35,55 71,1 17,775

13 -1 1 23,7 -23,7 23,7 -23,7 23,7 23,7

14 0 1 50,2 0 50,2 0 0 50,2

15 1 1 71,8 71,8 71,8 71,8 71,8 71,8

Сумма: 506,0 217,8 136,8 29,7 346,2 237,3

Коэффициенты модели вычисляются по формулам (6.7)

с использованием данных таблиц 16.16 и 3.

95,34)8,237*19048,0

2,346*2,0(506*29524,0)(

+−=−=

∑∑∑

=== u

iuuoi

XYAYАb

021,146,3*29524,0}{

===

Yoo

SAbS

;

78,218,217*1,0)(

111

===

∑

YxАb

;

136

24,188,136*1333,0)(

222

===

∑

YxАb

;

346,046,3*1,0}{

===

SAbS

;

461,046,3*1333,0}{

===

SAbS

;

;93,57,29*2,0)(

211212

===

∑

YxxАb

692,046,3*2,0}{

1212

===

SAbS

;

66,2506*2,02,346*3,0

11111

=−=−=

∑∑

== u

YAYxАb

;

98,5506*19048,03,237*42188,0

22222

−=−=−=

∑∑

== u

YAYxАb

038,146,3*3,0}{

1111

===

SAbS

;

459,146,3*42188,0}{

2222

===

SAbS

Проверка значимости коэффициентов уравнения прово-

дится по критерию Стюдента, критическое (табличное) зна-

чение которого для уровня значимости

05,0

и числа сте-

пеней свободы дисперсии воспроизводимости

30)13(*15)1(*

−

−= mNf

равно

04,2

)30;05,0(

62,34

01,1

95,34

}{

===

04,37

588,0

78,21

}{

===

86,26

679,0

24,18

}{

===

14,7

83,0

93,5

}{

===

61,2

018,1

66,2

}{

===

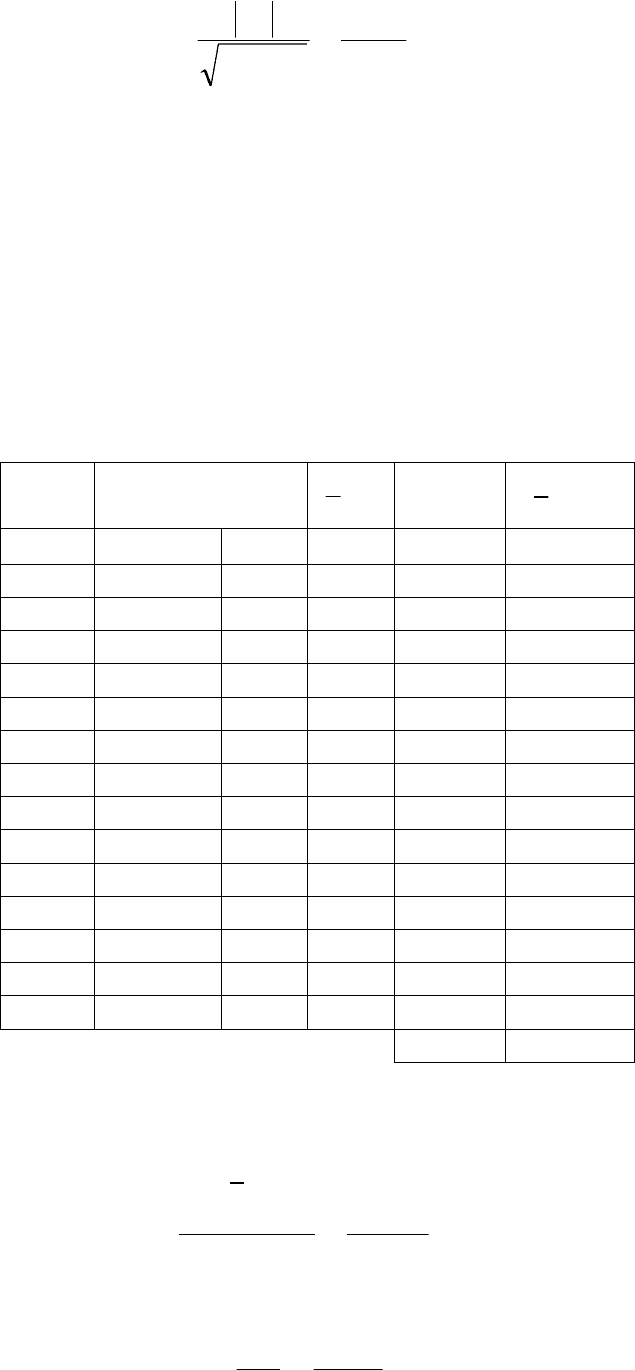
137

95,4

207,1

98,5

}{

===

Расчетные критерии Стьюдента всех коэффициентов

меньше табличного, поэтому нет достаточных оснований для

удаления какого-либо коэффициента из модели. Соответст-

венно уравнение регрессии примет вид:

2121

98,556,293,524,1878,2195,34 хххххху −++++=

Расчеты для определения дисперсии адекватности при-

ведены в таблице 4.

Таблица 4

№

опыта

Матрица плана

€

)

€

( yy −

1 -1 -1 2,2 -2,46 21,716

2 0 -1 10,1 10,72 0,384

3 1 -1 26,7 29,23 6,401

4 -1 -0,5 6,7 8,17 2,161

5 0 -0,5 21,6 24,33 7,453

6 1 -0,5 46,8 45,80 1,000

7 -1 0 12,7 15,83 9,797

8 0 0 32,6 34,95 5,523

9 1 0 65,6 59,39 38,564

10 -1 0,5 18,9 20,49 2,528

11 0 0,5 45,3 42,57 7,453

12 1 0,5 71,1 69,98 1,254

13 -1 1 23,7 22,15 2,403

14 0 1 50,2 47,20 9,000

15 1 1 71,8 77,57 33,293

Cумма: 148,929

Дисперсия адекватности составляет:

()

54,16

615

93,148

€

−

∑

ад

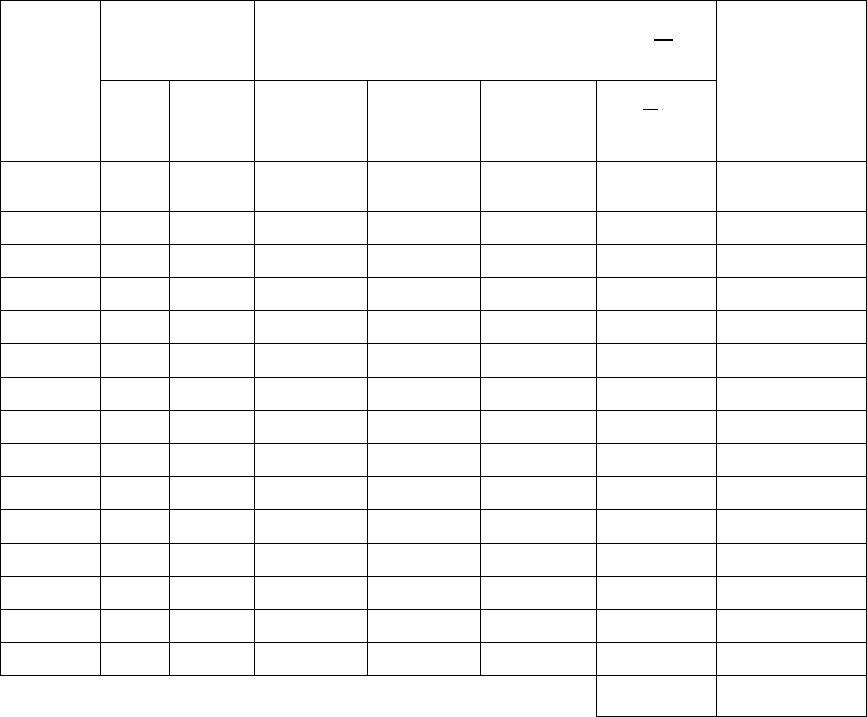
Расчетный критерий Фишера:

78,4

46,3

54,16

===

ад

138

Теоретическое значение критерия Фишера для уровня

значимости

05,0=

и числа степеней свободы

ад

составляет

21,2

)9;30;05,0(

, что меньше расчетно-

го. Следовательно, полученная модель неадекватно экспери-

менту и не может использоваться для описания процесса.

Кроме того, в первом опыте при минимальных уровнях вход-

ных факторов уравнение дает нефизическое (отрицательное)

значение целевой функции.

Для получения приемлемой модели воспользуемся

приемом, рекомендованным в пункте 6.2. А именно, предста-

вим модель (1) в

виде логарифмической функции:

222

1121122211

ln хbхbххbхbхbbуY

+++++==

Значения экспериментов в логарифмической системе пред-

ставлены в таблице 5.

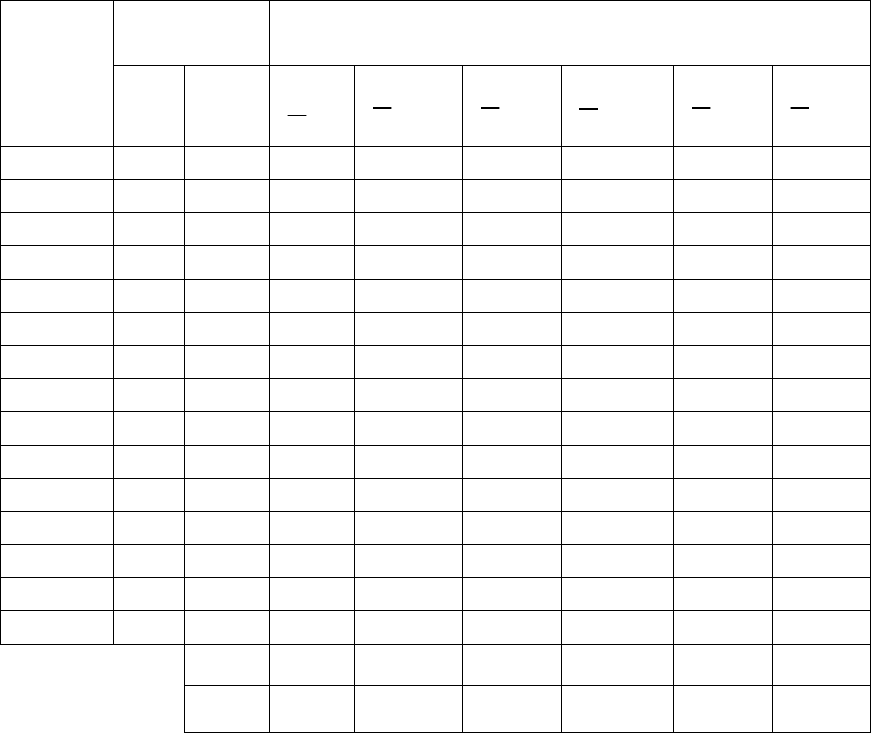
Таблица 5

Матрица

плана

Значение выходного параметра

сж

Rln

в опыте

и среднее

№

Опыта

yln

Дисперсия

опыта

уu

1 -1 -1

0,7884 0,8329 0,7419 0,7877 0,004139

2 0 -1 2,1972 2,4595 2,2617 2,3061 0,037378

3 +1 -1 3,2921 3,2464 3,3141 3,2842 0,002384

4 -1 -0,5 1,9600 1,7749 1,9600 1,8983 0,022852

5 0 -0,5 2,9750 3,1045 3,1311 3,0704 0,013858

6 +1 -0,5 3,8351 3,8264 3,8753 3,8456 0,001361

7 -1 0 2,5802 2,5877 2,4510 2,5396 0,011819

8 0 0 3,5351 3,4904 3,4242 3,4832 0,006224

9 +1 0 4,1820 4,2002 4,1682 4,1834 0,000515

10 -1 +0,5 2,9231 2,9652 2,9285 2,9389 0,001051

11 0 +0,5 3,7650 3,7909 3,8795 3,8121 0,007129

12 +1 +0,5 4,2180 4,2413 4,3294 4,2629 0,006903

13 -1 +1 3,2542 3,0726 3,1612 3,1627 0,016483

14 0 +1 3,8565 3,9219 3,9665 3,9149 0,006123

15 +1 +1 4,2696 4,2877 4,2640 4,2738 0,000305

∑

0,138523

139

Расчетная матрица плана для определения коэффициен-

тов модели представлена в таблице 6.

Таблица 6

Матрица

Плана

Расчетная матрица

№

Опыта

xxY

1 -1 -1 0,787 -0,787 -0,787 0,787 0,787 0,787

2 0 -1 2,306 0 -2,306 0 0 2,306

3 1 -1 3,284 3,284 -3,284 -3,284 3,284 3,284

4 -1 -0,5 1,898 -1,898 -0,949 0,949 1,898 0,474

5 0 -0,5 3,070 0 -1,535 0 0 0,767

6 1 -0,5 3,845 3,845 -1,922 -1,922 3,846 0,961

7 -1 0 2,539 -2,539 0 0 2,54 0

8 0 0 3,483 0 0 0 0 0

9 1 0 4,183 4,183 0 0 4,183 0

10 -1 0,5 2,938 -2,939 1,469 -1,469 2,939 0,734

11 0 0,5 3,812 0 1,906 0 0 0,953

12 1 0,5 4,262 4,262 2,131 2,131 4,263 1,065

13 -1 1 3,162 -3,162 3,162 -3,162 3,163 3,162

14 0 1 3,914 0 3,915 0 0 3,915

15 1 1 4,273 4,273 4,273 4,273 4,274 4,273

∑

47,76 8,52 6,07 -1,69 31,17 22,68

3,54 0,852 0,809 -0,339 -0,2 -0,455

После вычисления значений коэффициентов новое

уравнение регрессии принимает вид:

)455,02,0339,0809,0852,054,3(

2121

ххххххExpу −−−++=

6.4.4. Анализ полиномиальных моделей и особенности

проведения экспериментов

Получение многофакторной модели по сравнению с ко-

торыми зависимости

)(

xfy = ; )(

xfy

… )(

xfy

представляет-

ся заманчивой целью, но возникают определенные трудности

в её анализе. Конечно, и многофакторную модель содержа-

щую гораздо больше информации о системе, можно легко

140

преобразовать в однофакторные уравнения, но при этом те-

ряется сам смысл многофакторного исследования. Поэтому

анализ полученной модели необходимо проводить с учетом

всех возможностей, предоставляемых методом планирования

экспериментов.

Прежде всего необходимо определить цели анализа. Сре-

ди последних обычно выделяют:

определение величины выходного параметра сис-

темы в точках факторного пространства;

определение координат экстремума целевой функ-

ции;

оценка степени влияния фактора на параметр опти-

мизации;

оптимизация поведения системы (точек “наилуч-

шего” значения целевой функции) в пределах или

вне факторного пространства.

Определение значения целевой функции в любой точке А

внутри факторного пространства с координатами А(Z

; Z

;

;… Z

) по выражению:

111

...

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅+

−

⋅

−

⋅+

−

⋅+=

∑∑∑

=≤<≤=

oiiA

ojjA

oiiA

kji

oiiA

bby

6.1

где Z

и ΔZ

– значение фактора и его интервала варьирован-

ных в натуральных координатах в точке А.

Естественно, что при адекватной модели достоверные

значения

€

гарантируются только для точек находящихся

внутри факторного пространства. Но иногда (особенно в слу-

чае линейных моделей) при помощи полученного уравнения

можно прогнозировать значения целевой функции и для то-

чек лежащих вне границ экспериментальной области – экс-

трополяционная задача. Вычисление целевой функции про-

водят так же по уравнению (6.11) с соответствующими зна-