Лапин И.А., Ратафьева Л.С. Кратные интегралы. Теория поля
Подождите немного. Документ загружается.


61
ç‡È‰ÂÏ ‚˚ð‡ÊÂÌË ‰Îfl ˝ÚÓÈ ð‡·ÓÚ˚ Ò ÔÓÏÓ˘¸˛ ÍðË‚ÓÎËÌÂÈÌÓ„Ó
ËÌÚ„ð‡Î‡ ‚ÚÓðÓ„Ó ðÓ‰‡ (ðËÒ. 2.2.2). èÛÒÚ¸
α
– Û„ÓÎ ÏÂÊ‰Û Ì‡-
Ôð‡‚ÎÂÌËÂÏ Í‡Ò‡ÚÂθÌÓÈ, ÒÓ‚Ô‡‰‡˛˘ËÏ ÓÚ
A Í B Ë ÓÒ¸˛ Ox ;
β
–
Û„ÓÎ ÏÂÊ‰Û Ì‡Ôð‡‚ÎÂÌËÂÏ Í‡Ò‡ÚÂθÌÓÈ Ë ÓÒ¸˛
Oy ;
δ
– Û„ÓÎ ÏÂÊ-
‰Û ‚ÂÍÚÓðÓÏ
F
u
r
Ë ÓÒ¸˛ Ox . üÒÌÓ, ˜ÚÓ ()
θ
δα
=
±− .
é·ÓÁ̇˜ËÏ ˜ÂðÂÁ
(,)Pxy Ë (,)Qxy ÔðÓÂ͈ËË ÒËÎ˚ F
ur
̇ ÍÓÓð‰Ë-
̇ÚÌ˚ ÓÒË. é˜Â‚ˉÌÓ, ˜ÚÓ
(,)cos (,)Fxy Pxy
δ
⋅= , (,)sin (,)Fxy Qxy
δ
⋅
=
(Á‰ÂÒ¸ Ó·ÓÁ̇˜ÂÌÓ
(,) (,)Fxy Fxy=
ur
). äðÓÏÂ ÚÓ„Ó flÒÌÓ, ˜ÚÓ
cos cos( ) cos cos sin sin
θ
δα δ α δ α
=−= + ,
ÚÓ„‰‡
(
)
()
()
cos ( , )cos cos ( , )sin sin
(,)cos (,)sin
(,)cos (,)cos ,
AB AB
AB
AB
AFdS Fxy Fxy dS
Pxy Qxy dS
Pxy Qxy dS
δα δα
αα
αβ
== + =
=+=
=+
∫∫
∫
∫
u
r
Ú.Í.
2
π
αβ
+=, ÒΉӂ‡ÚÂθÌÓ sin cos
α
β
=
. ç‡ÍÓ̈, Û˜ËÚ˚‚‡fl
Ò‚flÁ¸ ÏÂÊ‰Û ÍðË‚ÓÎËÌÂÈÌ˚ÏË ËÌÚ„ð‡Î‡ÏË I Ë II ðÓ‰‡, ÓÍÓ̘‡-
ÚÂθÌÓ ÏÓÊÂÏ Ì‡ÔËÒ‡Ú¸:
(,) (,)
AB
APxydxQxydy=+
∫
.
àÚ‡Í, Ï˚ ÏÓÊÂÏ Û˜ËÚ˚‚‡Ú¸, ˜ÚÓ ‚ÒflÍËÈ ÍðË‚ÓÎËÌÂÈÌ˚È ËÌÚÂ-
„ð‡Î ‚ÚÓðÓ„Ó ðÓ‰‡ ‚ˉ‡
(,) (,)
AB
Pxydx Qxydy+
∫
ÏÓÊÌÓ ËÒÚÓÎÍÓ‚‡Ú¸ Í‡Í ð‡·ÓÚÛ ÒËÎ˚, Ëϲ˘ÂÈ Ò‚ÓËÏË ÔðÓÂ͈ËflÏË
̇ ÍÓÓð‰Ë̇ÚÌ˚ ÓÒË
(,)Pxy Ë (,)Qxy , ÔÓ ÔÂðÂÏ¢ÂÌ˲ χÚÂðË-
‡Î¸ÌÓÈ ÚÓ˜ÍË ‚‰Óθ ÍðË‚ÓÈ
AB ËÁ ÚÓ˜ÍË A ‚ ÚÓ˜ÍÛ B .
§3. îÓðÏÛ· ÉðË̇
èÛÒÚ¸ Á‡‰‡Ì‡ ÌÂÍÓÚÓð‡fl ӷ·ÒÚ¸
D
, Ó„ð‡Ì˘ÂÌ̇fl ÒÌËÁÛ ÍðË‚ÓÈ
()yx
ϕ
= , Ò‚ÂðıÛ – ÍðË‚ÓÈ ()yx
=
Φ , ‡ Ò ·ÓÍÓ‚ – ÓÚðÂÁ͇ÏË BC Ë
AD , Ô‡ð‡ÎÎÂθÌ˚ÏË ÓÒË Oy (ðËÒ. 2.3.1), Ë ÔÛÒÚ¸ ‚ ˝ÚÓÈ Ó·Î‡ÒÚË
ÓÔð‰ÂÎÂ̇ ÌÂÔðÂð˚‚̇fl ÙÛÌ͈Ëfl
(,)Pxy , Ëϲ˘‡fl ÌÂÔðÂð˚‚ÌÛ˛
˜‡ÒÚÌÛ˛ ÔðÓËÁ‚Ó‰ÌÛ˛
(,)
y
Pxy
′
.

62
Ç˚˜ËÒÎËÏ
(,)
D
Pxy
Idxdy
y
∂
=
∂
∫∫
.
èÂðÂıÓ‰fl Í ÔÓ‚ÚÓðÌÓÏÛ ËÌÚ„ð‡ÎÛ, ÔÓÎÛ˜ËÏ
()()
()
()
(,)
,() ,()
x
bb
ax a
Pxy
Idx dy PxxPxxdx
y
ϕ
ϕ
Φ
∂
⎡
⎤
==Φ−
⎣
⎦
∂
∫∫ ∫
.
ë ‰ðÛ„ÓÈ ÒÚÓðÓÌ˚, ËÌÚ„ð‡Î ÔÓ ÍÓÌÚÛðÛ Ó·Î‡ÒÚË
D :
[] [ ]
(,) (,) (,) (,) (,)
,() , () .
K
D
AB BC CD DA
bb
aa
Pxydx Pxydx Pxydx Pxydx Pxydx
Px x dx Px x dx
ϕ
=+++=
=−Φ
∫∫∫∫∫
∫∫
èð‡‚˚ ˜‡ÒÚË ‰‚Ûı ÔÓÒΉÌËı ÙÓðÏÛÎ ÓÚ΢‡˛ÚÒfl ÚÓθÍÓ Á̇-
ÍÓÏ, ÒΉӂ‡ÚÂθÌÓ,
(,)
(,)
K
D
D
Pxy
dxdy P x y dx
y
∂
=−
∂
∫∫ ∫
.
èÓÎÛ˜ÂÌ̇fl ÙÓðÏÛ· ̇Á˚‚‡ÂÚÒfl χÎÓÈ ÙÓðÏÛÎÓÈ ÉðË̇.
åÓÊÌÓ ‰Ó͇Á‡Ú¸, ˜ÚÓ Ó̇ ÒÔð‡‚‰ÎË‚‡ Ë ‰Îfl ӷ·ÒÚË, ËÁÓ·ð‡ÊÂÌÌÓÈ
̇ ðËÒ 2.3.2.
êËÒ. 2.3.1
A
B
x
0
y
D
C
D
b
a
()yx
ϕ
=
()yx
=
Φ
êËÒ. 2.3.2
x
0
y
D
d
c
()xy
ϕ
=
()xy
=
Φ

63
çÂÚðÛ‰ÌÓ ‰Ó͇Á‡Ú¸ Ú‡ÍÊÂ, ˜ÚÓ ˝Ú‡ ÙÓðÏÛ· ÒÔð‡‚‰ÎË‚‡ ‰Îfl β-
·ÓÈ Ó·Î‡ÒÚË, ð‡ÒÔ‡‰‡˛˘ÂÈÒfl ̇ ÍÓ̘ÌÓ ˜ËÒÎÓ ˜‡ÒÚÂÈ, ËÁÓ·ð‡-
ÊÂÌÌ˚ı ̇ ðËÒ. 2.3.1 Ë 2.3.2.
ÖÒÎË ‚ ӷ·ÒÚË
D ÓÔð‰ÂÎÂ̇ Ë ÌÂÔðÂð˚‚̇ ÙÛÌ͈Ëfl (,)Qxy ,
Ëϲ˘‡fl ÌÂÔðÂð˚‚ÌÛ˛ ˜‡ÒÚÌÛ˛ ÔðÓËÁ‚Ó‰ÌÛ˛
(,)Qxy
x
∂
∂
, ÚÓ ÒÓ‚Âð-
¯ÂÌÌÓ ‡Ì‡Îӄ˘ÌÓ ÏÓÊÌÓ ‰Ó͇Á‡Ú¸ ‚ÚÓðÛ˛ χÎÛ˛ ÙÓðÏÛÎÛ ÉðË-
̇:
(,)
(,)
K
D
D
Qxy
dxdy Q x y dy
x
∂
=
∂
∫∫ ∫
.
Ç˚˜ËÚ‡fl ÔÓ˜ÎÂÌÌÓ ËÁ ‚ÚÓðÓÈ ÔÂð‚Û˛ χÎÛ˛ ÙÓðÏÛÎÛ ÉðË̇, ÔÓ-
ÎÛ˜ËÏ Ú‡ÍÛ˛ ÙÓðÏÛÎÛ:
(,) (,)
(,) (,)
K
D
D
Qxy Pxy
dxdy P x y dx Q x y dy
xy
∂∂
⎡⎤
−=+
⎢⎥
∂∂
⎣⎦
∫∫ ∫
.
ùÚ‡ ÙÓðÏÛ· ̇Á˚‚‡ÂÚÒfl ·Óθ¯ÓÈ ÙÓðÏÛÎÓÈ ÉðË̇ ËÎË ÔðÓÒÚÓ
ÙÓðÏÛÎÓÈ ÉðË̇. é̇ ÛÒڇ̇‚ÎË‚‡ÂÚ Ò‚flÁ¸ ÏÂÊ‰Û ‰‚ÓÈÌ˚Ï ËÌÚÂ-
„ð‡ÎÓÏ ÔÓ Ó·Î‡ÒÚË
D Ë ÍðË‚ÓÎËÌÂÈÌ˚Ï ËÌÚ„ð‡ÎÓÏ ÔÓ ÍÓÌÚÛðÛ
˝ÚÓÈ Ó·Î‡ÒÚË.
á‡Ï˜‡ÌË (Ó ‚˚˜ËÒÎÂÌËË ÔÎÓ˘‡‰Ë ӷ·ÒÚË Ò ÔÓÏÓ˘¸˛ ÍðË-
‚ÓÎËÌÂÈÌÓ„Ó ËÌÚ„ð‡Î‡). èÓÎÓÊËÏ ‚ ÙÓðÏÛΠÉðË̇
(,)Pxy y
=
− ,
(,)Qxy x= ÚÓ„‰‡ ÔÓÎÛ˜ËÏ
11 2
(,) (,)Qxy Pxy
xy
∂∂
−
=+=
∂∂
.
èðË Ú‡ÍËı Á̇˜ÂÌËflı ÙÛÌ͈ËË
(,)Pxy Ë (,)Qxy ËÌÚ„ð‡Î,
ÒÚÓfl˘ËÈ ‚ ΂ÓÈ ˜‡ÒÚË ÙÓðÏÛÎ˚ ÉðË̇, ‰‡ÂÚ Ì‡Ï Û‰‚ÓÂÌÌÛ˛ ÔÎÓ-
˘‡‰¸ ӷ·ÒÚË
D , ÓÚÍÛ‰‡ ÒΉÛÂÚ
1
2
D
D
K
Sxdyydx=−
∫
.
èÓ ˝ÚÓÈ ÙÓðÏÛΠÏÓÊÌÓ ‚˚˜ËÒÎËÚ¸ ÔÎÓ˘‡‰¸ ӷ·ÒÚË
D , Ó„ð‡-
Ì˘ÂÌÌÓÈ ÍÓÌÚÛðÓÏ
D
K .
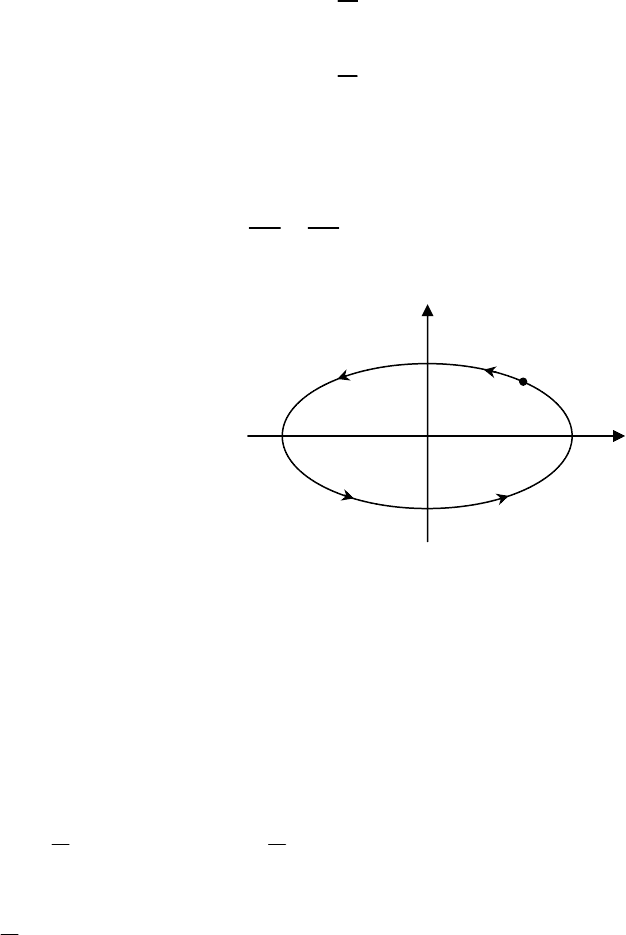
èðËÏÂð. Ç˚˜ËÒÎËÚ¸ ÔÎÓ˘‡‰¸, Ó„ð‡Ì˘ÂÌÌÛ˛ ÍðË‚ÓÈ
cos
sin
xa t
yb t
=
⎫
⎬
=
⎭
.
64
ê¯ÂÌËÂ. á‡Ô˯ÂÏ Ô‡ð‡ÏÂÚð˘ÂÒÍË Ûð‡‚ÌÂÌËfl ‰‡ÌÌÓÈ ÍðË‚ÓÈ
Ú‡Í
cos
sin
x
t
a
y
t
b
⎫
=
⎪
⎪
⎬
⎪
=
⎪
⎭
.
ÇÓÁ‚Ó‰fl ‚ Í‚‡‰ð‡Ú Ë ÒÍ·‰˚‚‡fl ÔÓ˜ÎÂÌÌÓ ˝ÚË Ûð‡‚ÌÂÌËfl, ÔÓÎÛ-
˜ËÏ Í‡ÌÓÌ˘ÂÒÍÓ Ûð‡‚ÌÂÌË ˝ÎÎËÔÒ‡
22
22
1
xy
ab
+=
(ðËÒ. 2.3.3).
ÑÎfl ‚˚˜ËÒÎÂÌËfl ÔÎÓ˘‡‰Ë ˝ÎÎËÔÒ‡, Ӊ̇ÍÓ, Û‰Ó·Ì ÓÒÚ‡‚ËÚ¸
Ô‡ð‡ÏÂÚð˘ÂÒÍË Ûð‡‚ÌÂÌËfl. é˜Â‚ˉÌÓ, ˜ÚÓ Ô‡ð‡ÏÂÚð
t ÏÂÌflÂÚÒfl ÓÚ
0 ‰Ó 2
π
(ÔðË ˝ÚÓÏ ÚÂÍÛ˘‡fl ÚӘ͇ (,)Mxy ӷ„‡ÂÚ ÔÓÎÌ˚È ÍÓÌÚÛð
˝ÎÎËÔÒ‡). ì˜ËÚ˚‚‡fl, ˜ÚÓ
sin
t
xat
′
=− , cos
t
yb t
′
=
, ÔÓÎÛ˜ËÏ:
2
0
11
22
элл
элл
cos cos ( sin ) ( sin )
K
Sxdyydxatbtatbtdt
π
=−=⋅+−⋅−=
∫∫
2
0
1
2
ab dt ab
π
π
==
∫
.
í.Â. Ï˚ ÔÓÎÛ˜ËÏ, ˜ÚÓ ÔÎÓ˘‡‰¸ ˝ÎÎËÔÒ‡
Sab
π
=
͂. ‰
.
èðË
ab= ÔÓÎÛ˜‡ÂÏ ËÁ‚ÂÒÚÌÛ˛ ÙÓðÏÛÎÛ ‰Îfl ÔÎÓ˘‡‰Ë ÍðÛ„‡
2
Sr
π
=
,
„‰Â Ó·ÓÁ̇˜ÂÌÓ
abr==.
x
y
(,)Mxy
aa−
b
−
b
êËÒ. 2.3.3

65
§4. äðË‚ÓÎËÌÂÈÌ˚ ËÌÚ„ð‡Î˚, Ì Á‡‚ËÒfl˘Ë ÓÚ ÔÛÚË
ËÌÚ„ðËðÓ‚‡ÌËfl
èÛÒÚ¸ ÙÛÌ͈ËË (,)Pxy Ë (,)Qxy ÓÔð‰ÂÎÂÌ˚ Ë ÌÂÔðÂð˚‚Ì˚ ‚
ÌÂÍÓÚÓðÓÈ ÓÚÍð˚ÚÓÈ Ó·Î‡ÒÚË
S Ë ËÏÂ˛Ú ‚ ÌÂÈ ÌÂÔðÂð˚‚Ì˚ ˜‡ÒÚ-
Ì˚ ÔðÓËÁ‚Ó‰Ì˚Â
(,)Qxy
x
∂
∂
Ë
(,)Pxy
y
∂
∂
. å˚ ·Û‰ÂÏ ð‡ÒÒχÚðË‚‡Ú¸
ÍðË‚˚Â, ˆÂÎËÍÓÏ ÎÂʇ˘Ë ‚ ӷ·ÒÚË
S Ë ‰ÓÔÛÒ͇˛˘Ë Ôð‰ÒÚ‡‚-
ÎÂÌËÂ
()
()
xt
yt
ϕ
ψ
=
⎫
⎬
=
⎭
,
Ôð˘ÂÏ ÙÛÌ͈ËË
()t
ϕ
Ë ()t
ψ
ÌÂÔðÂð˚‚Ì˚ Ë ËÏÂ˛Ú ÌÂÔðÂð˚‚Ì˚Â
ÔðÓËÁ‚Ó‰Ì˚Â
()t
ϕ
′
Ë ()t
ψ
′
ÔðË Î˛·ÓÏ [,]tpq
∈
ӷ·ÒÚË S Ë ‰ÓÔÛÒ-
͇˛˘Ë Ôð‰ÒÚ‡‚ÎÂÌËÂ
()xt
ϕ
=
, ()yt
ψ
=
, Ôð˘ÂÏ ÙÛÌ͈ËË ()t
ϕ
Ë
()t
ψ
ÌÂÔðÂð˚‚Ì˚ Ë ËÏÂ˛Ú ÌÂÔðÂð˚‚Ì˚ ÔðÓËÁ‚Ó‰Ì˚ ()t
ϕ
′
Ë ()t
ψ
′
ÔðË Î˛·ÓÏ
[,]tpq
∈
.
éÔð‰ÂÎÂÌË 1. ÉÓ‚ÓðflÚ, ˜ÚÓ ËÌÚ„ð‡Î
(,) (,)
AB
IPxydxQxydy=+
∫
Ì Á‡‚ËÒËÚ ÓÚ ÔÛÚË ËÌÚ„ðËðÓ‚‡ÌËfl,
ÂÒÎË ðÂÁÛθڇÚ˚ ËÌÚ„ðËðÓ‚‡ÌËfl ÔÓ Î˛·˚Ï ÍðË‚˚Ï, ÒÓ‰ËÌfl˛-
˘ËÏ ÚÓ˜ÍË
A
Ë
B
, ÒÓ‚Ô‡‰‡˛Ú, Ú.Â. ÂÒÎË
(,) (,) (,) (,)
AMB ANB
Pxydx Qxydy Pxydx Qxydy+= +
∫∫
(ðËÒ. 2.4.1).
á‡Ï˜‡ÌËÂ. àÌÚ„ð‡Î˚, Ì Á‡‚ËÒfl˘Ë ÓÚ ÔÛÚË ËÌÚ„ðËðÓ‚‡ÌËfl,
ËÌÓ„‰‡ Á‡ÔËÒ˚‚‡˛Ú Ú‡Í:
(,) (,)
B
A
IPxydxQxydy=+
∫
,
„‰Â
00
(,)Ax y Ë
11
(,)Bx y , ‡ ÔÓ‰ ÍðË‚ÓÈ, ÔÓ ÍÓÚÓðÓÈ ‚‰ÂÚÒfl ËÌÚ„ðË-
ðÓ‚‡ÌËÂ, ÔÓÌËχÂÏ Î˛·Û˛ ÍðË‚Û˛
AB , Î˯¸ ·˚ ̇ ÌÂÈ Ì ̇ðÛ-
¯‡ÎËÒ¸ ÛÒÎÓ‚Ëfl ÚÂÓðÂÏ˚ ÒÛ˘ÂÒÚ‚Ó‚‡ÌËfl ÍðË‚ÓÎËÌÂÈÌÓ„Ó ËÌÚ„ð‡-
·.
êËÒ. 2.4.1
x
0
y
A
B
N
M
S

66
éÔð‰ÂÎÂÌË 2. ÉÓ‚ÓðflÚ, ˜ÚÓ ËÌÚ„ð‡Î ÔÓ Á‡ÏÍÌÛÚÓÏÛ ÍÓÌ-
ÚÛðÛ ð‡‚ÂÌ ÌÛβ, ÂÒÎË ‰Îfl β·Ó„Ó Á‡ÏÍÌÛÚÓ„Ó Ò‡ÏÓÌÂÔÂðÂÒÂ͇˛-
˘Â„ÓÒfl ÍÓÌÚÓð‡
L
, ˆÂÎËÍÓÏ ÎÂʇ˘Â„Ó ‚
S
, Ó͇Á˚‚‡ÂÚÒfl
0(,) (,)
L
Pxydx Qxydy
+
=
∫
.
ãÂÏχ. éÔð‰ÂÎÂÌËfl 1 Ë 2 ˝Í‚Ë‚‡ÎÂÌÚÌ˚.
1. ÑÓ͇ÊÂÏ, ˜ÚÓ ÂÒÎË ÍðË‚ÓÎËÌÂÈÌ˚È ËÌÚ„ð‡Î Ì Á‡‚ËÒËÚ ÓÚ
ÔÛÚË ËÌÚ„ðËðÓ‚‡ÌËfl, ÚÓ ÔÓ Î˛·ÓÏÛ Á‡ÏÍÌÛÚÓÏÛ ÍÓÌÚÛðÛ ÓÌ ð‡‚ÂÌ
ÌÛβ (ðËÒ. 2.4.1).
ÑÂÈÒÚ‚ËÚÂθÌÓ ÔÛÒÚ¸
(,) (,) (,) (,)
AMB ANB
Pxydx Qxydy Pxydx Qxydy+= +
∫∫
.
éÚÒ˛‰‡ ÒΉÛÂÚ:
0
0
(,) (,) (,) (,)
(,) (,) (,) (,)
AMB ANB
AMB BNA
AMBNA
Pxydx Qxydy Pxydx Qxydy
Pxydx Qxydy Pxydx Qxydy
Pdx Qdy
+− +=⇒
⇒+++=
=+=
∫∫
∫∫
∫
.
íÂÔÂ𸠉ÓÒÚ‡ÚÓ˜ÌÓ ÚÓθÍÓ Ó·ÓÁ̇˜ËÚ¸ Á‡ÏÍÌÛÚÛ˛ ÍðË‚Û˛
AMBNA ·ÛÍ‚ÓÈ L Ë Ó͇ÊÂÚÒfl
0(,) (,)
L
Pxydx Qxydy
+
=
∫
.
2. ÇÚÓðÓ ÛÚ‚ÂðʉÂÌËÂ: ÂÒÎË ËÌÚ„ð‡Î ÔÓ Á‡ÏÍÌÛÚÓÏÛ ÍÓÌÚÛðÛ
ð‡‚ÂÌ ÌÛβ, ÚÓ ÓÌ Ì Á‡‚ËÒËÚ ÓÚ ÔÛÚË ËÌÚ„ðËðÓ‚‡ÌËfl, ‰Ó͇Á˚‚‡ÂÚ-
Òfl ‡Ì‡Îӄ˘ÌÓ, ‰Îfl ˜Â„Ó ‰ÓÒÚ‡ÚÓ˜ÌÓ ð‡Á·ËÚ¸ Á‡ÏÍÌÛÚ˚È ÍÓÌÚÛð
L
̇ ‰‚‡ Û˜‡ÒÚ͇
(‰Ó͇ÊËÚ ҇ÏÓÒÚÓflÚÂθÌÓ).
íÂÓðÂχ 1. ÑÎfl ÚÓ„Ó ˜ÚÓ·˚ ËÌÚ„ð‡Î
0(,) (,)
AB
IPxydxQxydy=+=
∫
Ì Á‡‚ËÒÂÎ ÓÚ ÔÛÚË ËÌÚ„ðËðÓ‚‡ÌËfl,
ÌÂÓ·ıÓ‰ËÏÓ Ë ‰ÓÒÚ‡ÚÓ˜ÌÓ, ˜ÚÓ·˚ ‚ ͇ʉÓÈ ÚӘ͠ӷ·ÒÚË
S ·˚ÎÓ
‚˚ÔÓÎÌÂÌÓ ÛÒÎÓ‚ËÂ
(,) (,)Qxy Pxy
xy
∂∂
=
∂∂
.
ÑÓ͇Á‡ÚÂθÒÚ‚Ó.
ÑÓÒÚ‡ÚÓ˜ÌÓÒÚ¸. ÑÓÔÛÒÚËÏ, ˜ÚÓ ‚ ͇ʉÓÈ ÚӘ͠ӷ·ÒÚË
S ‚˚-
ÔÓÎÌÂÌÓ ÛÒÎÓ‚Ë (1). ÇÓÁ¸ÏÂÏ Á‡ÏÍÌÛÚ˚È Ò‡ÏÓÌÂÔÂðÂÒÂ͇˛˘ËÈÒfl
(1)
67
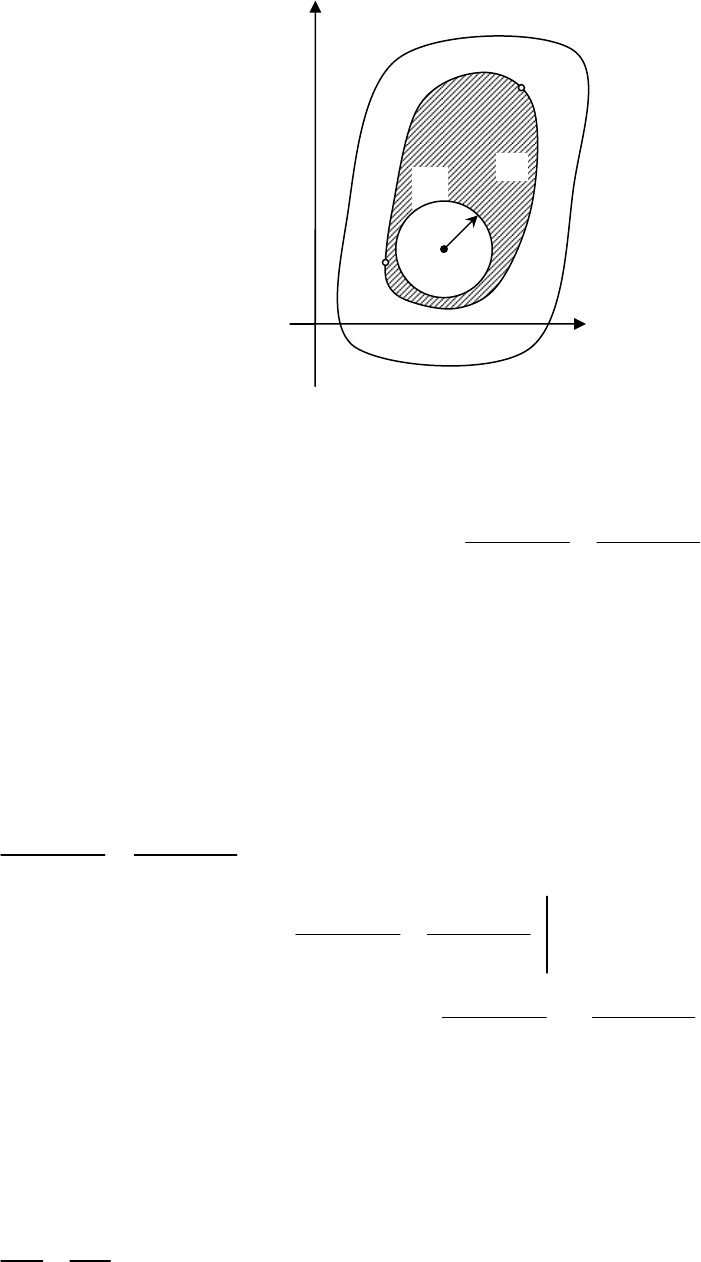
ÍÓÌÚÛð
K , ÎÂʇ˘ËÈ ‚ S Ë Ó„ð‡Ì˘˂‡˛˘ËÈ Ó·Î‡ÒÚ¸ D (ðËÒ.
2.4.2).
Ç ÒËÎÛ ÙÓðÏÛÎ˚ ÉðË̇:
(,) (,)
(,) (,)
LD
Qxy Pxy
P x y dx Q x y dy dxdy
xy
∂∂
⎛⎞
+= −
⎜⎟
∂∂
⎝⎠
∫∫∫
.
í‡Í Í‡Í ‚˚ÔÓÎÌÂÌÓ ÛÒÎÓ‚Ë (1), ÚÓ
0(,) (,)
L
Pxydx Qxydy+=
∫
, ‡
ÚÓ„‰‡ ‚ ÒËÎÛ ÎÂÏÏ˚ ÍðË‚ÓÎËÌÂÈÌ˚È ËÌÚ„ð‡Î
(,) (,)
AB
Pxydx Qxydy+
∫
Ì Á‡‚ËÒËÚ ÓÚ ÔÛÚË ËÌÚ„ðËðÓ‚‡ÌËfl.
çÂÓ·ıÓ‰ËÏÓÒÚ¸. ÑÓÔÛÒÚËÏ, ˜ÚÓ ÛÒÎÓ‚Ë (1) Ì ‚˚ÔÓÎÌÂÌÓ ‚Ò˛‰Û ‚
S Ë ÔÛÒÚ¸ ̇ȉÂÚÒfl ÌÂÍÓÚÓð‡fl ÚӘ͇
000
(,)Mxy
, ‚ ÍÓÚÓðÓÈ
(,) (,)Qxy Pxy
xy
∂∂
≠
∂∂
. èÛÒÚ¸ ‰Îfl ÓÔð‰ÂÎÂÌÌÓÒÚË ‚ ˝ÚÓÈ ÚÓ˜ÍÂ
0
0
(,) (,)
M
Qxy Pxy
xy
∂∂
⎛⎞
−
>
⎜⎟
∂∂
⎝⎠
.
í‡Í Í‡Í ˜‡ÒÚÌ˚ ÔðÓËÁ‚Ó‰Ì˚Â
(,)Qxy
x
∂
∂
Ë
(,)Pxy
y
∂
∂
ÌÂÔðÂð˚‚Ì˚,
ÚÓ ÏÓÊÌÓ Ì‡ÈÚË ÍðÛ„
ρ
Δ
Ò ˆÂÌÚðÓÏ ‚ ÚÓ˜ÍÂ
0
M ÒÚÓθ χÎÓ„Ó ð‡-
‰ËÛÒ‡
ρ
, ˜ÚÓ ÔÓÒΉÌ ÌÂð‡‚ÂÌÒÚ‚Ó ‚˚ÔÓÎÌflÂÚÒfl ‚Ó ‚ÒÂı ÚӘ͇ı
ӷ·ÒÚË
ρ
Δ . èÛÒÚ¸ L
ρ
– ÍÓÌÚÛð ӷ·ÒÚË
ρ
Δ
. ÑÎfl ˝ÚÓÈ Ó·Î‡ÒÚË
ÒÔð‡‚‰ÎË‚‡ ÙÓðÏÛ· ÉðË̇, ÌÓ Ú.Í. ‚ ͇ʉÓÈ ÚӘ͠ӷ·ÒÚË
ρ
Δ
:
0
QP
xy
∂∂
−>
∂∂
, ÚÓ ‰‚ÓÈÌÓÈ ËÌÚ„ð‡Î
B
L
ρ
êËÒ. 2.4.2
x
0
y
A
S
D
ρ
0
M
ρ
Δ
L

68
0
QP
dxdy
xy
ρ
Δ
∂∂
⎛⎞
−
>
⎜⎟
∂∂
⎝⎠
∫∫
,
ÒΉӂ‡ÚÂθÌÓ, ̇¯ÂÎÒfl ÍÓÌÚÛð
ρ
Δ
Ú‡ÍÓÈ, ˜ÚÓ
0(,) (,)
L
Pxydx Qxydy
ρ
+
≠
∫
.
íÂÓðÂχ ‰Ó͇Á‡Ì‡.
íÂÓðÂχ 2. ÖÒÎË ‚ ͇ʉÓÈ ÚӘ͠ӷ·ÒÚË
S ÙÛÌ͈ËË (,)Pxy Ë
(,)Qxy ÌÂÔðÂð˚‚Ì˚ Ë ËÏÂ˛Ú ÌÂÔðÂð˚‚Ì˚ ˜‡ÒÚÌ˚ ÔðÓËÁ‚Ó‰Ì˚Â
(,) (,)Qxy Pxy
xy
∂∂
=
∂∂
, ÚÓ ‚˚ð‡ÊÂÌË (,) (,)Pxydx Qxydy
+
fl‚ÎflÂÚÒfl
ÔÓÎÌ˚Ï ‰ËÙÙÂðÂ̈ˇÎÓÏ ÌÂÔðÂð˚‚ÌÓÈ ÙÛÌ͈ËË
(,)
(,)
(,) (,) (,)
xy
ab
xy Pxydx QxydyΦ= +
∫
,
Ú.Â.
(,) (,) (,)dxy PxydxQxydyΦ= + .
ÑÓ͇Á‡ÚÂθÒÚ‚Ó. èÛÒÚ¸ ‚ ͇ʉÓÈ ÚӘ͠ӷ·ÒÚË
S ‚˚ÔÓÎÌÂÌÓ
ÛÒÎÓ‚Ë (1). á‡ÍðÂÔËÏ ÚÓ˜ÍÛ
(,)Aab Ë ÔÛÒÚ¸ (,)Mxy – ͇͇fl-
ÌË·Û‰¸ ÚӘ͇ ӷ·ÒÚË
S . íÓ„‰‡ (,) (,)
AM
Pxydx Qxydy+
∫
Á‡‚ËÒËÚ Ó
ÚÓ˜ÍË
M , ÌÓ Ì Á‡‚ËÒËÚ ÓÚ ÎËÌËË AM .
ùÚÓ ÓÁ̇˜‡ÂÚ, ˜ÚÓ Ì‡ÔËÒ‡ÌÌ˚È ËÌÚ„ð‡Î fl‚ÎflÂÚÒfl ÙÛÌ͈ËÂÈ ÔÂ-
ðÂÏÂÌÌ˚ı
x Ë y . é·ÓÁ̇˜ËÏ Â ˜ÂðÂÁ (,)xy
Φ
, ÚÓ„‰‡ ÏÓÊÌÓ Ì‡ÔË-
Ò‡Ú¸:
(,)
(,)
(,) (,) (,)
xy
ab
xy Pxydx QxydyΦ= +
∫
.
èÓÔðÓ·ÛÂÏ ÔðÓ‰ËÙÙÂðÂ̈ËðÓ‚‡Ú¸ ÙÛÌÍˆË˛
(,)xy
Φ
ÔÓ ÔÂðÂÏÂÌ-
ÌÓÈ
x (ðËÒ. 2.4.3).
êËÒ. 2.4.3
x 0
y
A
(,)Nx xy
+
Δ
x
Δ
(,)Mxy
S

69
ÑÎfl ˝ÚÓ„Ó, ËÒıÓ‰fl ËÁ ÚÓ˜ÍË
(,)Mxy , ‰‡‰ËÏ ÔðËð‡˘ÂÌË x
Δ
,
‚Áfl‚ Â„Ó ÒÚÓθ χÎ˚Ï, ˜ÚÓ·˚ ÓÚðÂÁÓÍ
MN , ÒÓ‰ËÌfl˛˘ËÈ ÚÓ˜ÍË
(,)Mxy Ë (,)Nx xy+Δ , ˆÂÎËÍÓÏ ÎÂʇΠ‚ ӷ·ÒÚË S , ÚÓ„‰‡ ·Û‰ÂÚ
(,)
(,)
(,) ( ,)
(,) (,)
(,)
(,)
(,) (,)(,)
(,) ( ,) (,) .
xxy
ab
xy x xy
ab xy
xxy
xy
xxy PxydxQxydy
Pdx Qdy Pdx Qdy
xy x xy xy Pdx Qdy
+Δ
+Δ
+Δ
Φ+Δ = + =
=++ +⇒
⇒ΔΦ =Φ +Δ −Φ = +
∫
∫∫
∫
.
Ç˚ð‡ÁËÏ ÍðË‚ÓÎËÌÂÈÌ˚È ËÌÚ„ð‡Î, ÒÚÓfl˘ËÈ ‚ Ôð‡‚ÓÈ ˜‡ÒÚË,
˜ÂðÂÁ ÓÔð‰ÂÎÂÌÌ˚È, Û˜ËÚ˚‚‡fl, ˜ÚÓ Ì‡ ÓÚðÂÁÍÂ
MN
y
ÔÓÒÚÓflÌÂÌ,
Ú.Â.
0dy = , ‡ [, ]xxx x∈+Δ. íÓ„‰‡ ÔÓÎÛ˜ËÏ
(,) (,)
xx
x
xy Pxydx
+Δ
ΔΦ =
∫
.
èðËÏÂÌËÏ Í ÓÔð‰ÂÎÂÌÌÓÏÛ ËÌÚ„ð‡ÎÛ, ÒÚÓfl˘ÂÏÛ ÒÔð‡‚‡, ÚÂÓðÂ-
ÏÛ Ó Òð‰ÌÂÏ, ÚÓ„‰‡ ·Û‰ÂÚ
(,) (,)xy P y x
ξ
Δ
Φ= ⋅Δ, Ôð˘ÂÏ
xxx
ξ
≤≤+Δ, ÚÓ„‰‡
00
lim lim ( , ) ( , )
xx
PyPxy
x
ξ
Δ→ Δ→
Δ
Φ
==
Δ
.
àÚ‡Í, Ï˚ ÔÓÎÛ˜ËÎË
0
(,) ( ,) (,)
lim ( , )
x
xy x xy xy
Pxy
xx
Δ→
∂Φ Φ + Δ − Φ
==
∂Δ
.
Ä̇Îӄ˘ÌÓ ÏÓÊÌÓ ‰Ó͇Á‡Ú¸, ˜ÚÓ ˜‡ÒÚ̇fl ÔðÓËÁ‚Ӊ̇fl
(,)xy
y
∂Φ
∂
Ú‡ÍÊ ÒÛ˘ÂÒÚ‚ÛÂÚ, Ôð˘ÂÏ
(,)
(,)
xy
Qxy
y
∂
Φ
=
∂
. ëΉӂ‡ÚÂθÌÓ, ÙÛÌÍ-
ˆËfl
(,)xyΦ ‰ËÙÙÂðÂ̈ËðÛÂχ, Ôð˘ÂÏ
(,) (,) (,)dxy PxydxQxydyΦ= + .
ëΉÒÚ‚ËÂ. èÓ Ôð‰ÔÓÎÓÊÂÌ˲ ÚÂÓðÂÏ˚
(,)Pxy Ë (,)Qxy ÌÂ-
ÔðÂð˚‚Ì˚, ÒΉӂ‡ÚÂθÌÓ ÌÂÔðÂð˚‚Ì˚
(,)
x
xy
′
Φ
Ë (,)
y
xy
′
Φ , ‡ ÚÓ„‰‡
ÌÂÔðÂð˚‚̇ Ë Ò‡Ï‡ ÙÛÌ͈Ëfl
(,)xy
Φ
.
á‡Ï˜‡ÌËÂ. ÑÓ͇Á‡Ì̇fl ÚÂÓðÂχ ‰‡ÂÚ Ì‡Ï ‚ÓÁÏÓÊÌÓÒÚ¸ ̇ıÓ‰ËÚ¸
ÙÛÌÍˆË˛
(,)xyΦ ÔÓ Â ÔÓÎÌÓÏÛ ‰ËÙÙÂðÂ̈ˇÎÛ Ò ÔÓÏÓ˘¸˛ ÍðË‚Ó-
ÎËÌÂÈÌÓ„Ó ËÌÚ„ð‡Î‡. ÑÎfl ˝ÚÓ„Ó ÌÛÊÌÓ Á‡ÍðÂÔËÚ¸ ͇ÍÛ˛-ÌË·Û‰¸
70
ÚÓ˜ÍÛ
(,)ab , ‡ Á‡ÚÂÏ, ‚Áfl‚ ÔðÓËÁ‚ÓθÌÛ˛ ÚÓ˜ÍÛ (,)xy , ÒÓ‰ËÌËÚ¸ Ëı
͇ÍÛ˛-ÌË·Û‰¸ ÔðÓÒÚÓÈ ÍðË‚ÓÈ
L Ë ‚˚˜ËÒÎËÚ¸ (,)xyΦ=
(,)
(,)
(,) (,)
xy
ab
Pxydx Qxydy=+
∫
, Î˯¸ ·˚ ÚÓθÍÓ Ì‡ ˝ÚÓÈ ÍðË‚ÓÈ ·˚ÎË
‚˚ÔÓÎÌÂÌ˚ ÛÒÎÓ‚Ëfl ÚÂÓðÂÏ˚ ÒÛ˘ÂÒÚ‚Ó‚‡ÌËfl ÍðË‚ÓÎËÌÂÈÌÓ„Ó ËÌÚÂ-
„ð‡Î‡ ‚ÚÓðÓ„Ó ðÓ‰‡.
ÑÓ͇Á‡ÌÌ˚ ‚˚¯Â ‰‚ ÚÂÓðÂÏ˚ ÔÓÁ‚ÓÎfl˛Ú ÒÙÓðÏÛÎËðÓ‚‡Ú¸ Ú‡-
ÍÛ˛ Ó·˘Û˛ ÚÂÓðÂÏÛ.
íÂÓðÂχ. ÖÒÎË ‚ ӷ·ÒÚË
S Á‡‰‡Ì˚ ÌÂÔðÂð˚‚Ì˚ ÙÛÌ͈ËË
(,)Pxy Ë (,)Qxy , Ëϲ˘Ë ÌÂÔðÂð˚‚Ì˚ ˜‡ÒÚÌ˚ ÔðÓËÁ‚Ó‰Ì˚Â
(,)Pxy
y
∂
∂
Ë
(,)Qxy
x
∂
∂
, ÚÓ Î˛·˚ ËÁ ÒÎÂ‰Û˛˘Ëı ÛÚ‚ÂðʉÂÌËÈ ð‡‚ÌÓ-
ÒËθÌ˚ (Ú.Â. ËÁ Ó‰ÌÓ„Ó ÒΉÛÂÚ ‰ðÛ„ÓÂ Ë Ì‡Ó·ÓðÓÚ):
1.
(,) (,)
AB
Pxydx Qxydy+
∫
Á‡‚ËÒËÚ ÓÚ ÚÓ˜ÂÍ
A
Ë
B
, ÌÓ ÌÂ ÓÚ
ÍðË‚ÓÈ
AB .
2. ä‡ÍÓ‚ ·˚ ÌË ·˚Î Á‡ÏÍÌÛÚ˚È Ò‡ÏÓÌÂÔÂðÂÒÂ͇˛˘ËÈÒfl ÍÓÌÚÛð
L
, ËÏÂÂÏ:
0(,) (,)
L
Pxydx Qxydy
+
=
∫
.
3. ÇÒ˛‰Û ‚
S :
(,) (,)Pxy Qxy
yx
∂∂
=
∂∂
.
4. Ç˚ð‡ÊÂÌËÂ
(,) (,)Pxydx Qxydy+ ÂÒÚ¸ ÔÓÎÌ˚È ‰ËÙÙÂðÂ̈ˇÎ
ÌÂÍÓÚÓðÓÈ ÙÛÌ͈ËË
(,)xyΦ .
èðËÏÂð. ì·Â‰ËÚ¸Òfl, ˜ÚÓ ‚˚ð‡ÊÂÌËÂ
22
2dx ydy
xy xy
+
+
+
fl‚ÎflÂÚÒfl
ÔÓÎÌ˚Ï ‰ËÙÙÂðÂ̈ˇÎÓÏ ÌÂÍÓÚÓðÓÈ ÙÛÌ͈ËË Ë Ì‡ÈÚË ÂÂ Ò ÔÓÏÓ-
˘¸˛ ÍðË‚ÓÎËÌÂÈÌÓ„Ó ËÌÚ„ð‡Î‡ ‚ÚÓðÓ„Ó ðÓ‰‡.
ê¯ÂÌËÂ. èðÂʉ ‚Ò„Ó, ۷‰ËÏÒfl, ˜ÚÓ Ôð˂‰ÂÌÌÓ ‚˚ð‡ÊÂÌËÂ
fl‚ÎflÂÚÒfl ÔÓÎÌ˚Ï ‰ËÙÙÂðÂ̈ˇÎÓÏ ÌÂÍÓÚÓðÓÈ ÙÛÌ͈ËË
(,)xyΦ .
é·ÓÁ̇˜ËÏ
2
1
(,)Pxydx
xy
=
+
,
2
2
(,)
y
Qxydy
xy
=
+
.
ç‡È‰ÂÏ
