Лапин И.А., Ратафьева Л.С. Кратные интегралы. Теория поля
Подождите немного. Документ загружается.


11
ÒÚ‚ÂÌÌÓ, ÚÓ ‚ ӷ·ÒÚË
D ̇ȉÂÚÒfl ÌÂÍÓÚÓð‡fl ÚӘ͇ (,)P
ξ
η
ڇ͇fl,
˜ÚÓ
1
(,) (,)
D
D
fxydxdy f
S
ξ
η
=
∫∫
,
ÓÚÍÛ‰‡ ÒΉÛÂÚ, ˜ÚÓ
(,) (,)
D
D
fxydxdy f S
ξη
=
⋅
∫∫
.
á̇˜ÂÌËÂ
(,)f
ξ
η
̇Á˚‚‡˛Ú «Òð‰ÌËÏ» Á̇˜ÂÌËÂÏ ÙÛÌ͈ËË ‚ Ó·-
·ÒÚË
D .
4. Ç˚˜ËÒÎÂÌË ‰‚ÓÈÌÓ„Ó ËÌÚ„ð‡Î‡.
Ç˚˜ËÒÎËÏ ‰‚ÓÈÌÓÈ ËÌÚ„ð‡Î
(,)
D
I f x y dxdy=
∫
∫
‚ Ôð‰ÔÓÎÓÊÂÌËË,
˜ÚÓ ÙÛÌ͈Ëfl
(,)fxy ÔÓÎÓÊËÚÂθ̇ ‚ ӷ·ÒÚË
D
, ‡ ӷ·ÒÚ¸
D
Ó„-
ð‡Ì˘Â̇ ÒÌËÁÛ ÍðË‚ÓÈ
1
()yyx
=
, Ò‚ÂðıÛ ÍðË‚ÓÈ
2
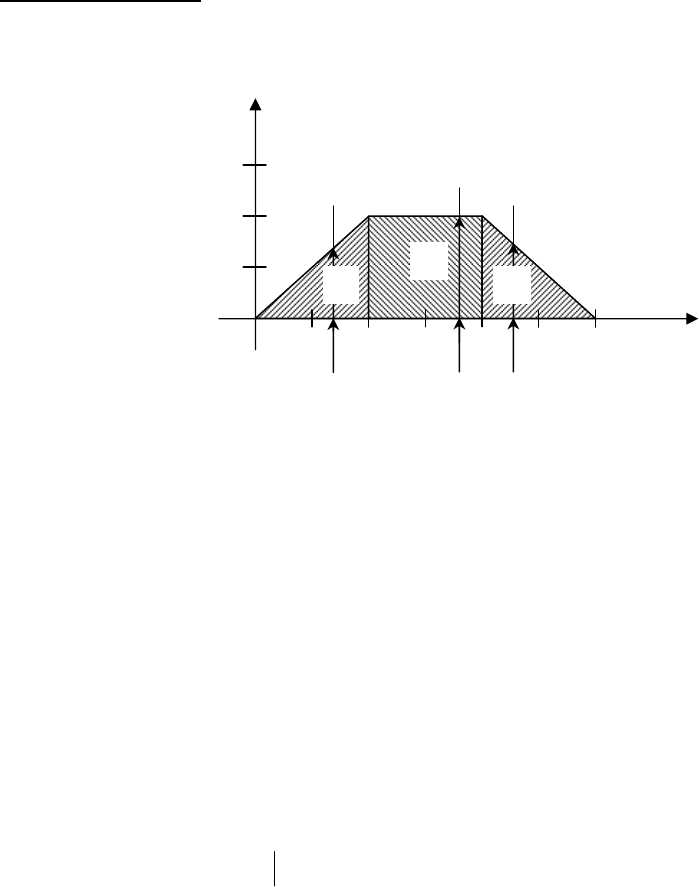
()yyx= (ðËÒ.
1.1.7), Ôð˘ÂÏ
[,]xab∈ . å˚ Ôð‰ÔÓ·„‡ÂÏ, ˜ÚÓ ÙÛÌ͈ËË
1
()yx
Ë
2
()yx ÌÂÔðÂð˚‚Ì˚ ̇ ÔðÓÏÂÊÛÚÍ [,]ab Ë ‚ ͇ʉÓÈ Â„Ó ÚÓ˜ÍÂ
12
() ()yx yx≤ . àÁ „ÂÓÏÂÚð˘ÂÒÍÓ„Ó ÒÏ˚Ò· ‰‚ÓÈÌÓ„Ó ËÌÚ„ð‡Î‡ flÒÌÓ,
˜ÚÓ ‰‚ÓÈÌÓÈ ËÌÚ„ð‡Î
(,)
D
fxydxdy
∫
∫
‰‡ÂÚ Ì‡Ï Ó·˙ÂÏ Ú·, ËÁÓ·ð‡-
ÊÂÌÌÓ„Ó Ì‡ ðËÒ. 1.1.7.
êËÒ. 1.1.7
x
y
z
0
()Fx
b
a
c
d
2
()yyx=
1
()yyx=
x
12
ç‡È‰ÂÏ Ó·˙ÂÏ ˝ÚÓ„Ó Ú· Ò ÔÓÏÓ˘¸˛ ÓÔð‰ÂÎÂÌÌÓ„Ó ËÌÚ„ð‡Î‡.
ÑÎfl ˝ÚÓ„Ó Ôðӂ‰ÂÏ Ò˜ÂÌË Ú· ÔÎÓÒÍÓÒÚ¸˛
xconst
=
. é·ÓÁ̇˜ËÏ
ÔÎÓ˘‡‰¸ ˝ÚÓ„Ó Ò˜ÂÌËfl
()Fx . àÁ‚ÂÒÚÌÓ, ˜ÚÓ Ó·˙ÂÏ Ú· ÔÓ ÔÎÓ˘‡-
‰flÏ Ò˜ÂÌËÈ ‚˚˜ËÒÎflÂÚÒfl Ú‡Í:
()
b
a
vFxdx=
∫
.
éÒÚ‡ÂÚÒfl ̇ÈÚË ÔÎÓ˘‡‰¸ Ò˜ÂÌËfl
()Fx . é˜Â‚ˉÌÓ, ˜ÚÓ ˝ÚÓ Ò˜Â-
ÌË Ôð‰ÒÚ‡‚ÎflÂÚ ÒÓ·Ó˛ ÍðË‚ÓÎËÌÂÈÌÛ˛ Úð‡ÔÂˆË˛, Ó„ð‡Ì˘ÂÌÌÛ˛
ÒÌËÁÛ ÔðflÏÓÈ
xconst= , Ò‚ÂðıÛ – ÍðË‚ÓÈ, Ûð‡‚ÌÂÌË ÍÓÚÓðÓÈ
(,)zfxy= (Ôð˘ÂÏ Á‰ÂÒ¸ x ÙËÍÒËðÓ‚‡ÌÓ), ‡ Ò ·ÓÍÓ‚ – ÔðflÏ˚ÏË,
Ô‡ð‡ÎÎÂθÌ˚ÏË ÓÒË
Oz
.
ëΉӂ‡ÚÂθÌÓ,
2
1
()
()
() (,)
yx
yx
Fx fxydy=
∫
.
èÓ‰ÒÚ‡‚Îflfl ̇ȉÂÌÌÓ Á̇˜ÂÌËÂ
()Fx ‚ ËÒıÓ‰Ì˚È ËÌÚ„ð‡Î,
ÓÍÓ̘‡ÚÂθÌÓ ÔÓÎÛ˜ËÏ:
2
1
()
()
(,) (,)
yx
b
Dayx
fxydxdy fxydydx
⎡
⎤
=
⎢
⎥
⎢
⎥
⎣
⎦
∫∫ ∫ ∫
.
àÌÚ„ð‡Î, ÒÚÓfl˘ËÈ ‚ Ôð‡‚ÓÈ ˜‡ÒÚË ˝ÚÓ„Ó ð‡‚ÂÌÒÚ‚‡, ̇Á˚‚‡ÂÚÒfl
ÔÓ‚ÚÓðÌ˚Ï ËÎË ‰‚ÛÍð‡ÚÌ˚Ï Ë Á‡ÔËÒ˚‚‡ÂÚÒfl Ú‡Í:
22
11
() ()
() ()
(,) (,)
yx yx
bb
ayx a yx
fxydydx dx fxydy
⎡⎤
=
⎢⎥
⎢⎥
⎣⎦
∫∫ ∫ ∫
.
àÚ‡Í, ÓÍÓ̘‡ÚÂθÌÓ ÔÓÎÛ˜‡ÂÏ Ú‡ÍÓ ‚˚ð‡ÊÂÌË ‰‚ÓÈÌÓ„Ó ËÌÚÂ-
„ð‡Î‡ ˜ÂðÂÁ ÔÓ‚ÚÓðÌ˚È:
2
1
()
()
(,) (,)
yx
b
Dayx
fxydxdy dx fxydy=
∫∫ ∫ ∫
.
á‡ÏÂÚËÏ, ˜ÚÓ ËÌÚ„ð‡Î
2
1
()
()
(,)
yx
yx
fxydy
∫
̇Á˚‚‡ÂÚÒfl ‚ÌÛÚðÂÌÌËÏ,
ÔðË ˝ÚÓÏ „Ó‚ÓðflÚ, ˜ÚÓ ‚ÌÛÚðÂÌÌ ËÌÚ„ðËðÓ‚‡ÌË ‚‰ÂÚÒfl ÔÓ ÔÂðÂ-
ÏÂÌÌÓÈ
y , ‡ ‚̯Ì – ÔÓ ÔÂðÂÏÂÌÌÓÈ x (ðËÒ. 1.1.7).
èðÓ‚Ó‰fl ÒÓ‚Âð¯ÂÌÌÓ ‡Ì‡Îӄ˘Ì˚ ð‡ÒÒÛʉÂÌËfl, Ï˚ ÏÓÊÂÏ ÔÓ-
ÎÛ˜ËÚ¸ ÚÓ˜ÌÓ Ú‡ÍÛ˛ Ê ÙÓðÏÛÎÛ ‰Îfl ‚˚˜ËÒÎÂÌËfl ‰‚ÓÈÌÓ„Ó ËÌÚÂ-
13
„ð‡Î‡, „‰Â ‚ÌÛÚðÂÌÌ ËÌÚ„ðËðÓ‚‡ÌË ‚˚ÔÓÎÌÂÌÓ ÔÓ ÔÂðÂÏÂÌÌÓÈ
x , ‡ ‚̯Ì – ÔÓ ÔÂðÂÏÂÌÌÓÈ y :
2
1
()
()
(,) (,)
xy
d
Dcxy
fxydxdy dy fxydx=
∫∫ ∫ ∫
.
é˜Â‚ˉÌÓ, ˜ÚÓ Ì ˄ð‡ÂÚ ðÓÎË, ÔÓ Í‡ÍÓÈ ÔÂðÂÏÂÌÌÓÈ ‚˚ÔÓÎÌflÂÚ-
Òfl ‚ÌÛÚðÂÌÌ ËÌÚ„ðËðÓ‚‡ÌËÂ, ‡ ÔÓ Í‡ÍÓÈ – ‚̯ÌÂÂ.
èðËÏÂð 1. Ç˚˜ËÒÎËÚ¸ ÔÎÓ˘‡‰¸ ӷ·ÒÚË
D
, Ó„ð‡Ì˘ÂÌÌÓÈ ÍðË-
‚˚ÏË
yx=
,
6xy+=
,
2y
=
,
0y
=
Ò ÔÓÏÓ˘¸˛ ‰‚ÓÈÌÓ„Ó ËÌÚ„ð‡Î‡
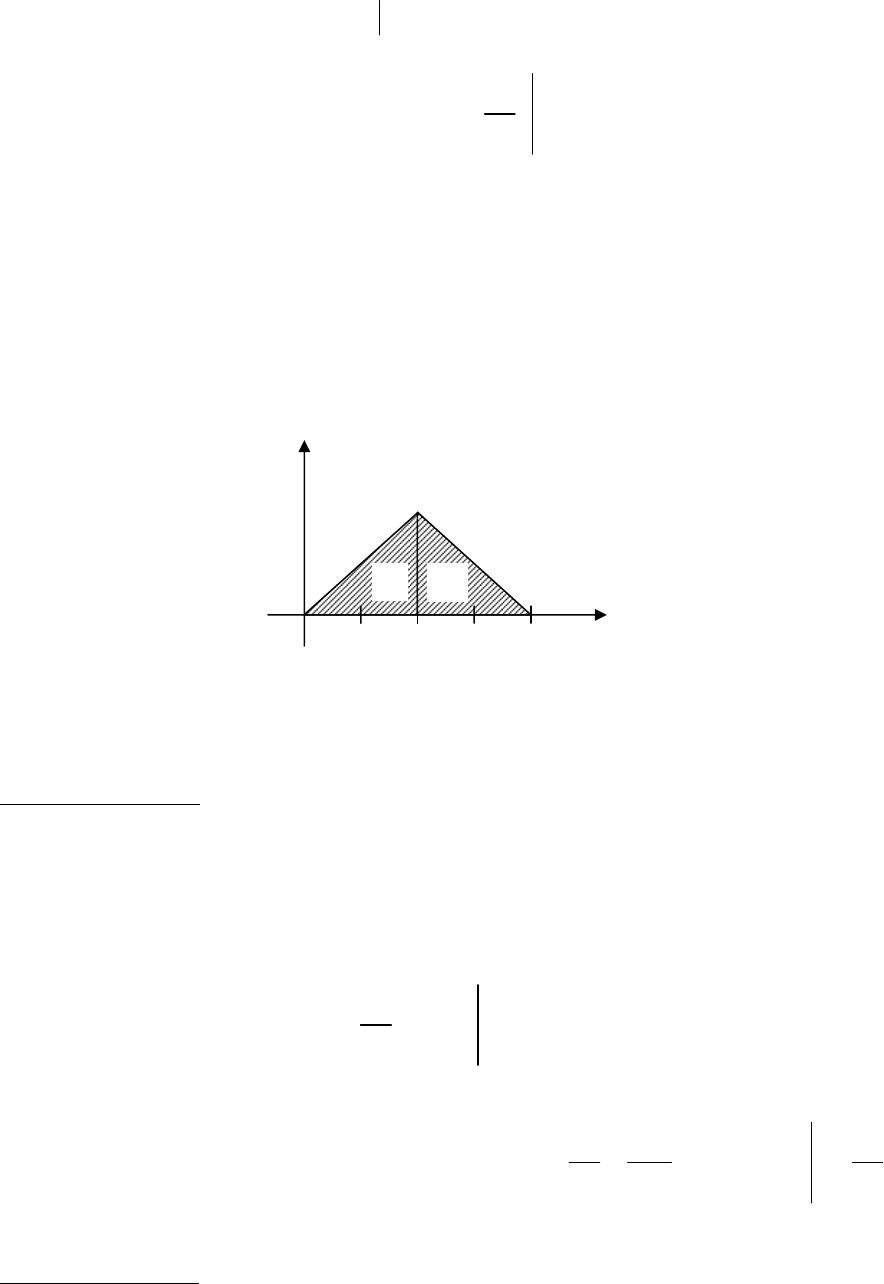
(ðËÒ. 1.1.8).
ê¯ÂÌËÂ. ê¯ËÏ Á‡‰‡˜Û ‰‚ÛÏfl ÒÔÓÒÓ·‡ÏË.
èÂð‚˚È ÒÔÓÒÓ·.
ê‡ÁÓ·¸ÂÏ Ó·Î‡ÒÚ¸ D ̇ ÚðË Ó·Î‡ÒÚË
1
D
,
2
D
Ë
3
D , Ôðӂ‰fl ÔðflÏ˚ 2x
=
Ë 4x
=
(ðËÒ. 1.1.8).
íÓ„‰‡ ËÒÍÓχfl ÔÎÓ˘‡‰¸
123
DD D D
SS S S
=
++, „‰Â
1
1
D
D
Sdxdy=
∫∫
,
2
2
D
D
Sdxdy=
∫∫
,
3
3
D
D
Sdxdy=
∫∫
.
Ç˚˜ËÒÎËÏ Í‡Ê‰˚È ËÁ ËÌÚ„ð‡ÎÓ‚, ‚˚ÔÓÎÌflfl ‚ÌÛÚðÂÌÌ ËÌÚ„-
ðËðÓ‚‡ÌË ÔÓ ÔÂðÂÏÂÌÌÓÈ
y , ‡ ‚̯Ì – ÔÓ ÔÂðÂÏÂÌÌÓÈ x . íÓ„‰‡
ÔÓÎÛ˜ËÏ:
1
1
2
00
x
D
D
Sdxdydxdy==
∫
∫∫∫
.
á‰ÂÒ¸
1
0
0
внутр
x
x
Idyyx===
∫
éÍÓ̘‡ÚÂθÌÓ ÔÓÎÛ˜ËÏ:
x
y
0
êËÒ. 1.1.8
yx
=
2y
=
6xy
+
=
2 4
6
1
D
3
D
2
D
2

14
1
2
2
22
0
0
2
2
22
D
x
Sxdx====
∫
.
á‡ÏÂÚËÏ, ˜ÚÓ ‰Îfl ̇ıÓʉÂÌËfl Ôð‰ÂÎÓ‚ ‚ÌÛÚðÂÌÌÂ„Ó ËÌÚ„ðËðÓ-
‚‡ÌËfl ÔÓ ÔÂðÂÏÂÌÌÓÈ
y
ÒΉÛÂÚ ˜ÂðÂÁ ӷ·ÒÚ¸
1
D ÔðÓ‚ÂÒÚË Ôðfl-
ÏÛ˛, Ô‡ð‡ÎÎÂθÌÛ˛ ÓÒË
Oy Ë ÔÓÒÏÓÚðÂÚ¸, ÔðË Í‡ÍÓÏ Á̇˜ÂÌËË y
Ó̇ ‚ıÓ‰ËÚ ‚ ӷ·ÒÚ¸
1
D Ë ÔðË Í‡ÍÓÏ Á̇˜ÂÌËË y Ó̇ ËÁ ӷ·ÒÚË
1
D
‚˚ıÓ‰ËÚ. ùÚÓ Ë ·Û‰ÛÚ Ôð‰ÂÎ˚ ËÌÚ„ðËðÓ‚‡ÌËfl. Ä ËÏÂÌÌÓ: ‚ıÓ-
‰ËÏ ‚ ӷ·ÒÚ¸
1
D ÔðË 0y = (ÌËÊÌËÈ Ôð‰ÂÎ ËÌÚ„ðËðÓ‚‡ÌËfl), ‡
‚˚ıÓ‰ËÏ ËÁ ӷ·ÒÚË ÔðË
yx= (˜ÂðÂÁ ÔðflÏÛ˛, Ûð‡‚ÌÂÌËfl ÍÓÚÓðÓÈ
yx= ; ˝ÚÓ ‚ÂðıÌËÈ Ôð‰ÂÎ ËÌÚ„ðËðÓ‚‡ÌËfl ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ).
ëÓ‚Âð¯ÂÌÌÓ ‡Ì‡Îӄ˘ÌÓ:
2
2
42
20
D
D
Sdxdydxdy==
∫∫ ∫ ∫
,
2
2
0
0
2
2 внутр
Idyy
=
==
∫
;
2
4
44
22
2
22 2 2424()
D
Sdxdxx===⋅=−=
∫∫
.
3
3
66
40
x
D
D
Sdxdydxdy
−
==
∫∫ ∫ ∫
,
6
6
0
0
6
3 внутр
x
x
Idyyx
−
−
=
==−
∫
;
3
6
6
2
4
4
36 16
6 6 36 24 18 16 2
222
()
D
x
Sxdxx
⎛⎞
⎛⎞⎛⎞
=− = − =− −− =−=
⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
⎝⎠
∫
.
é˜Â‚ˉÌÓ, ˜ÚÓ
123
2428
DD D D
SS S S=++=++=.
àÚ‡Í,
8
D
S
=
.
ÇÚÓðÓÈ ÒÔÓÒÓ·.
Ç˚·Ëð‡fl ‚ÌÛÚðÂÌÌ ËÌÚ„ðËðÓ‚‡ÌË ÔÓ ÔÂðÂ-
ÏÂÌÌÓÈ
x , ‡ ‚̯Ì ÔÓ ÔÂðÂÏÂÌÌÓÈ y , ÏÓÊÂÏ Á‡ÔËÒ‡Ú¸ ËÒÍÓÏÛ˛
ÔÎÓ˘‡‰¸ Ú‡Í:
6
2
0
y
D
Dy
Sdxdydydx
−
==
∫∫ ∫ ∫
.
á‡ÏÂÚËÏ, ˜ÚÓ ÔðË Ì‡ıÓʉÂÌËË Ôð‰ÂÎÓ‚ ‚ÌÛÚðÂÌÌÂ„Ó ËÌÚ„ðËðÓ-
‚‡ÌËfl (ÔÓ ÔÂðÂÏÂÌÌÓÈ
x ), Ï˚ Ï˚ÒÎÂÌÌÓ Ôðӂ‰ÂÏ ÔðflÏÛ˛, Ô‡ð‡Î-
ÎÂθÌÛ˛ ÓÒË
Ox . é̇ ‚ıÓ‰ËÚ ‚ ӷ·ÒÚ¸ D ÔðË xy
=
, ‡ ‚˚ıÓ‰ËÚ –
˜ÂðÂÁ ÔðflÏÛ˛, Ûð‡‚ÌÂÌË ÍÓÚÓðÓÈ
6xy
+
= , Ú.Â. ÔðË 6xy=−. á‡-
ÍÓ̘ËÏ ‚˚˜ËÒÎÂÌËÂ:
15
6
6
662
внутр
()
y
y
y
y
Idxx yyy
−
−
===−−=−
∫
;
2
2
2
0
0
62 6 2 1248
2
()
D
y
Sydyy
⎛⎞
=− = −⋅ =−=
⎜⎟
⎝⎠
∫
,
Ú.Â. Í‡Í Ë ÔðË ÔÂð‚ÓÏ ÒÔÓÒÓ·Â ð¯ÂÌËfl, Ï˚ ÔÓÎÛ˜ËÎË, ˜ÚÓ
8
D
S
=
.
èðËÏÂð 2. Ç˚˜ËÒÎËÚ¸:
2
()
D
Ixydxdy=+
∫
∫
,
„‰Â ӷ·ÒÚ¸
D Ó„ð‡Ì˘Â̇ ÔðflÏ˚ÏË 0y
=
, yx
=
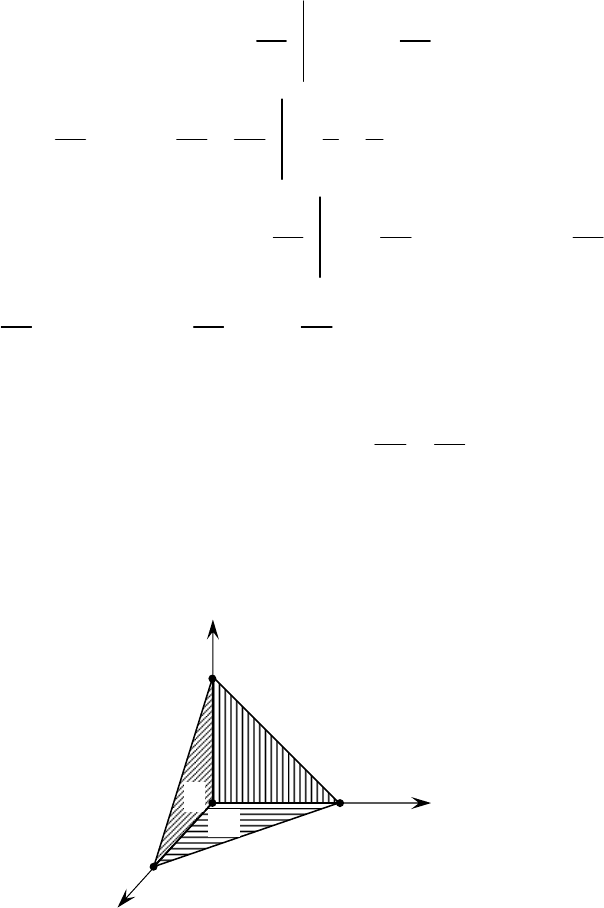
, 4xy+= (ðËÒ.
1.1.9).
ê¯ÂÌËÂ. ê¯ËÏ ÔðËÏÂ𠉂ÛÏfl ÒÔÓÒÓ·‡ÏË.
èÂð‚˚È ÒÔÓÒÓ·.
Ç˚ÔÓÎÌËÏ ‚ÌÛÚðÂÌÌ ËÌÚ„ðËðÓ‚‡ÌË ÔÓ ÔÂðÂ-
ÏÂÌÌÓÈ
x
, ‡ ‚̯Ì – ÔÓ
y
, ÚÓ„‰‡ ÔÓÎÛ˜ËÏ:
4
2
2
0
()
y
y
Idyxydx
−
=+
∫∫
.
Ç˚˜ËÒÎËÏ ‚ÌÛÚðÂÌÌËÈ ËÌÚ„ð‡Î:
4
4
2
2232
2448
2
внутр
()
y
y
y
y
x
Ixydxxyyyy
−
−
⎛⎞
=+ =+ =−+−+
⎜⎟
⎝⎠
∫
.
èÓ‰ÒÚ‡‚Îflfl ̇ȉÂÌÌÓ Á̇˜ÂÌË ‚ ‚˚ð‡ÊÂÌË ‰Îfl
I , ÔÓÎÛ˜ËÏ:
2
2
43
232 2
0
0
432
2448 28
23 3
()
D
yy
Ixydxdy yyydy yy
⎛⎞
⎡⎤
=+ =−+−+=−+−+ =
⎜⎟
⎣⎦
⎝⎠
∫∫ ∫
.
ÇÚÓðÓÈ ÒÔÓÒÓ·.
ÇÌÛÚðÂÌÌ ËÌÚ„ðËðÓ‚‡ÌË ‚˚ÔÓÎÌËÏ ÔÓ ÔÂðÂ-
ÏÂÌÌÓÈ
y , ‡ ‚̯Ì – ÔÓ x . á‡ÏÂÚËÏ, ˜ÚÓ ÔðË ˝ÚÓÏ Ó·Î‡ÒÚ¸ D
Ï˚ ‰ÓÎÊÌ˚ ð‡Á·ËÚ¸ ̇ ‰‚ ӷ·ÒÚË
1
D Ë
2
D (Í‡Í Û͇Á‡ÌÓ Ì‡ ðËÒ.
x
y
0
êËÒ. 1.1.9
yx
=
4xy
+
=
2 4
1
D
2
D
1
3
16
1.1.9); ÒΉӂ‡ÚÂθÌÓ, ‰‚ÓÈÌÓÈ ËÌÚ„ð‡Î ‚˚ð‡ÁËÚÒfl ‚ ‚ˉ ÒÛÏÏ˚
Ú‡ÍËı ‰‚Ûı ÔÓ‚ÚÓðÌ˚ı ËÌÚ„ð‡ÎÓ‚:
244
22
12
00 2 0
() ()
xx
IdxxydydxxydyII
−
=++ +=+
∫∫ ∫ ∫
.
33
22
0
0
33
1 внутр
()
x
x
yx
Ixydyxy x
⎛⎞
=
+=+=+
⎜⎟
⎝⎠
∫
;
2
2
334
2
0
0
84
4
331233
1
xxy
Ix dx
⎛⎞⎛⎞
=+ =+ =+=
⎜⎟⎜⎟
⎝⎠⎝⎠
∫
.
4
4
33
22
0
0
64
12 3
33 3
2 внутр
()
x
x
yx
Ixydyxy xx
−
−
⎛⎞
=+ =+ =−+−
⎜⎟
⎝⎠
∫
;
4
3
2
2
64 20
12 3
333
1
x
Ixxdx
⎛⎞
=−+− =
⎜⎟
⎝⎠
∫
.
àÚ‡Í, ÓÍÓ̘‡ÚÂθÌÓ ÔÓÎÛ˜ËÏ:
12
20 32
4
33
II I=+=+ = .
èðËÏÂð 3. Ç˚˜ËÒÎËÚ¸ Ó·˙ÂÏ Ú·, Ó„ð‡Ì˘ÂÌÌÓ„Ó ÔÎÓÒÍÓÒÚ¸˛
1xyz++= Ë ÍÓÓð‰Ë̇ÚÌ˚ÏË ÔÎÓÒÍÓÒÚflÏË 0x
=
, 0y
=
, 0z = .
ê¯ÂÌËÂ. èðËÌËχfl ‚Ó ‚ÌËχÌË „ÂÓÏÂÚð˘ÂÒÍËÈ ÒÏ˚ÒÎ ‰‚ÓÈ-
ÌÓ„Ó ËÌÚ„ð‡Î‡, Ï˚ ÏÓÊÂÏ Ì‡ÔËÒ‡Ú¸, ˜ÚÓ
T
D
v zdxdy=
∫
∫
.
á‰ÂÒ¸
D
– ÚðÂÛ„ÓθÌËÍ, ÎÂʇ˘ËÈ ‚ ÓÒÌÓ‚‡ÌËË ÔËð‡Ïˉ˚, ‡
z =
1 xy=− − , Ú.Â.
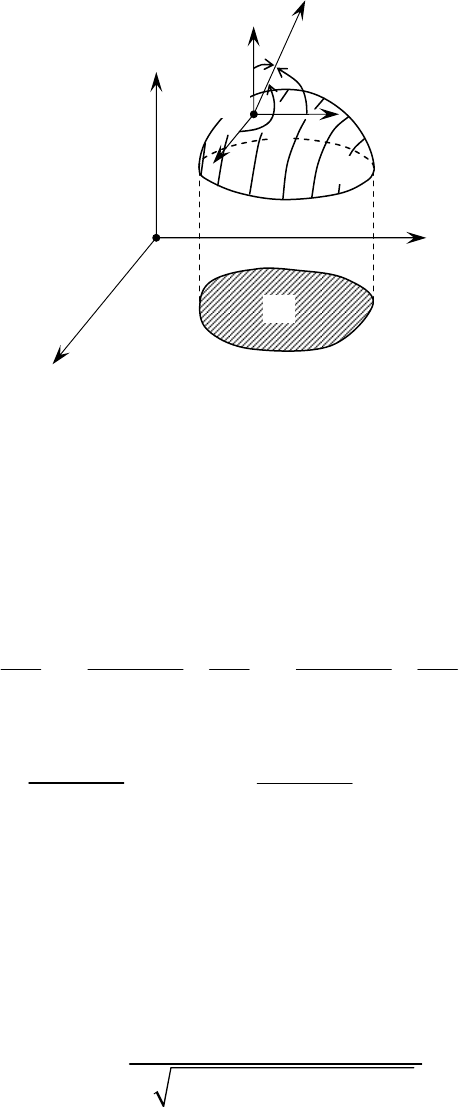
êËÒ. 1.1.10
x
y
z
0
1
1
1
A
C
B
D
1xy
+
=

17
11
00
11() ()
x
T
D
vxydxdydxxydy
−
=−− = −−
∫∫ ∫ ∫
.
ÇÌÛÚðÂÌÌËÈ ËÌÚ„ð‡Î:
1
1
222
2
0
0
11
11 1
222
внутр
()()
( ) () ()
x
x
yxx
Ixydyxy x
−
−
⎡⎤
−−
=−− =−⋅− =−− =
⎢⎥
⎣⎦
∫
.
ëΉӂ‡ÚÂθÌÓ,
1
11
23
22
00
0
11 1 1
12
22 2 36
()
()
T
xx
vdxxxdxxx
⎛⎞
−
==−+=−+=
⎜⎟
⎝⎠
∫∫
,
Ú.Â. ËÒÍÓÏ˚È Ó·˙ÂÏ Ú·
T ð‡‚ÂÌ
1
6
T
v
=
.
á‡Ï˜‡ÌËÂ. á‡ÏÂÚËÏ, ˜ÚÓ ËÒÍÓÏ˚È Ó·˙ÂÏ Ï˚ ÏÓ„ÎË ·˚ ̇ÈÚË,
ÔÓθÁÛflÒ¸ Á̇ÌËflÏË, ÔÓÎÛ˜ÂÌÌ˚ÏË ‚ Òð‰ÌÂÈ ¯ÍÓÎÂ. ÑÂÈÒÚ‚ËÚÂθ-
ÌÓ, ÚÂÎÓ
T ÂÒÚ¸ Ì ˜ÚÓ ËÌÓÂ, Í‡Í ÔËð‡Ïˉ‡, ÔÎÓ˘‡‰¸ ÓÒÌÓ‚‡ÌËfl ÍÓ-
ÚÓðÓÈ ÂÒÚ¸ ÔðflÏÓÛ„ÓθÌ˚È ÚðÂÛ„ÓθÌËÍ
AOB
, Ôð˘ÂÏ
111
11
222
AOB
SOAOB
Δ
=⋅ ⋅ =⋅⋅=. Ç˚ÒÓÚ‡ ÔËð‡Ïˉ˚ 1hOC==.
1
3
пир осн
vSh
=
⋅ , Ú.Â.
11 1
1
32 6
пир
v
=
⋅⋅=.
5. Ç˚˜ËÒÎÂÌË ÔÎÓ˘‡‰Ë ÍðË‚ÓÈ ÔÓ‚ÂðıÌÓÒÚË Ò ÔÓÏÓ˘¸˛
‰‚ÓÈÌÓ„Ó ËÌÚ„ð‡Î‡.
ê‡ÒÒÏÓÚðËÏ ÔÓ‚ÂðıÌÓÒÚ¸, Á‡‰‡ÌÌÛ˛ Ûð‡‚ÌÂÌËÂÏ
0(,,)Fxyz
=
.
ÑÓÔÛÒÚËÏ, ˜ÚÓ ÙÛÌ͈Ëfl
(,,)Fxyz ÌÂÔðÂð˚‚̇ Ë ËÏÂÂÚ ÌÂÔðÂð˚‚-
Ì˚ ˜‡ÒÚÌ˚ ÔðÓËÁ‚Ó‰Ì˚Â
x
F
′
,
y
F
′
,
z
F
′
. ÑÓÔÛÒÚËÏ, ˜ÚÓ ‚Ò ÚðË ˜‡ÒÚ-
Ì˚ ÔðÓËÁ‚Ó‰Ì˚ ÌÂ Ó·ð‡˘‡˛ÚÒfl ‚ ÌÓθ ÌË ‚ Ó‰ÌÓÈ ÚӘ͠ÔÓ‚Âðı-
ÌÓÒÚË
S , Ú.Â. ÔÓ‚ÂðıÌÓÒÚ¸ S ‚ ͇ʉÓÈ ÚӘ͠ËÏÂÂÚ Í‡Ò‡ÚÂθÌÛ˛
ÔÎÓÒÍÓÒÚ¸. å˚ ÛÒÚ‡ÌÓ‚ËÎË ð‡ÌÂÂ, ˜ÚÓ ÔðË Ú‡ÍËı Ôð‰ÔÓÎÓÊÂÌËflı ‚
͇ʉÓÈ ÚÓ˜ÍÂ
M ÔÓ‚ÂðıÌÓÒÚË S ÒÛ˘ÂÒÚ‚ÛÂÚ ÌÓðχθ Í ÔÓ‚ÂðıÌÓ-
ÒÚË
N
uur
, Ôð˘ÂÏ
(,,) (,,) (,,)
i
j
k
MM
M
Fxyz Fxyz Fxyz
N
xyz
∂∂∂
=
⋅+ ⋅+ ⋅
∂∂∂
uurrrur
.
18
ÑÓÔÛÒÚËÏ, ‚ ˜‡ÒÚÌÓÒÚË, ˜ÚÓ ÔÓ‚ÂðıÌÓÒÚ¸
S Á‡‰‡Ì‡ Ûð‡‚ÌÂÌËÂÏ
(,)zfxy= . é˜Â‚ˉÌÓ, ˜ÚÓ Ï˚ ÏÓÊÂÏ Ò˜ËÚ‡Ú¸
(,,) (,)Fxyz z fxy
=
− ,
Ôð˘ÂÏ, ˜‡ÒÚÌ˚ ÔðÓËÁ‚Ó‰Ì˚Â
(,)Ffxy
xx
∂∂
=−
∂∂
,
(,)Ffxy
yy
∂
∂
=−
∂∂
, 1
F
z
∂
=
∂
ÌÂÔðÂð˚‚Ì˚ ‚ ÒËÎÛ Ò‰Â·ÌÌ˚ı ‚˚¯Â Ôð‰ÔÓÎÓÊÂÌËÈ. é·ÓÁ̇˜ËÏ
(,)
(,)
fxy
pxy
x
∂
=
∂
,
(,)
(,)
fxy
qxy
y
∂
=
∂
.
íÓ„‰‡ flÒÌÓ, ˜ÚÓ ÌÓðχθ Í ÔÓ‚ÂðıÌÓÒÚË ‚ β·ÓÈ ÚÓ˜ÍÂ
M
·Û‰ÂÚ
ËÏÂÚ¸ ÍÓÓð‰Ë̇Ú˚:
(
)
1(,), (,),NN pxy qxy=− −
uuruur
.
Ö‰ËÌ˘Ì˚È ‚ÂÍÚÓð ÌÓðχÎË Í ÔÓ‚ÂðıÌÓÒÚË, ÒΉӂ‡ÚÂθÌÓ, ËÏÂ-
ÂÚ ‚ˉ:
0
22
1
(,)i (,)
j
k
(,) (,)
pxy qxy
N
pxy qxy
−⋅−⋅+
=
±++
r
rur
uur
,
„‰Â
i
r
,
j
r
, k
ur
– ÓðÚ˚ ÒËÒÚÂÏ˚ ÍÓÓð‰ËÌ‡Ú (ðËÒ. 1.1.11).
ä‡Í ËÁ‚ÂÒÚÌÓ, ÍÓÓð‰Ë̇Ú˚ ‰ËÌ˘ÌÓ„Ó ‚ÂÍÚÓð‡ ÒÓ‚Ô‡‰‡˛Ú Ò Ì‡-
Ôð‡‚Îfl˛˘ËÏË ÍÓÒËÌÛÒ‡ÏË ‰‡ÌÌÓ„Ó ‚ÂÍÚÓð‡. é·ÓÁ̇˜ËÏ ˜ÂðÂÁ
λ
,
μ
Ë
ν
Û„Î˚ ÌÓðχÎË N
u
ur
ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ Ò ÍÓÓð‰Ë̇ÚÌ˚ÏË ÓÒflÏË Ox ,
Oy , Oz . áÌ‡Í ± ‚ Á̇ÏÂ̇ÚÂΠÔÓÒΉÌÂÈ ÙÓðÏÛÎ˚ ÓÁ̇˜‡ÂÚ, ˜ÚÓ
Ï˚ ÏÓÊÂÏ ‚˚·ð‡Ú¸ ̇ ÌÓðχÎË ‰‚‡ ‚Á‡ËÏÌÓ ÔðÓÚË‚ÓÔÓÎÓÊÌ˚ı ̇-
êËÒ. 1.1.11
x
y
z
0
D
ν
μ
λ
M
S
N
u
ur
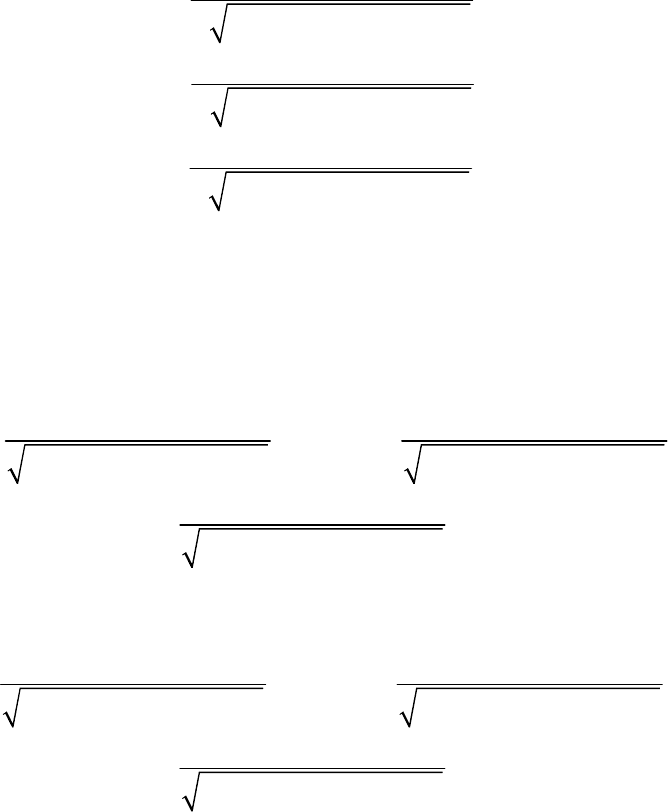
19
Ôð‡‚ÎÂÌËfl, Ú.Â. ‰Îfl ̇Ôð‡‚Îfl˛˘Ëı ÍÓÒËÌÛÒÓ‚ ÌÓðχÎË ÔÓÎÛ˜ËÏ
Ú‡ÍË ÙÓðÏÛÎ˚:
22
1
(,)
cos
(,) (,)
pxy
pxy qxy
λ
−
=
±
++
;
22
1
(,)
cos
(,) (,)
qxy
pxy qxy
μ
−
=
±
++
;
22
1
1
cos
(,) (,)
pxy qxy
ν
=
±
++
.
á‡ÙËÍÒËðÛÂÏ Ì‡ ÌÓðχÎË ÚÓ Ì‡Ôð‡‚ÎÂÌËÂ, ÍÓÚÓðÓ ӷð‡ÁÛÂÚ ÓÒÚ-
ð˚È Û„ÓÎ Ò ÓÒ¸˛
Oz
, Ú.Â. ‚˚·ÂðÂÏ ‚ ÙÓðÏÛ·ı ‰Îfl ̇Ôð‡‚Îfl˛˘Ëı
ÍÓÒËÌÛÒÓ‚ Ú‡ÍÓÈ ÁÌ‡Í ÔÂð‰ ÍÓðÌÂÏ, ˜ÚÓ·˚ ·˚ÎÓ
0cos
ν
> .
àÚ‡Í, ̇Ôð‡‚Îfl˛˘Ë ÍÓÒËÌÛÒ˚ ‰Îfl ÌÓðχÎË, Ó·ð‡ÁÛ˛˘ÂÈ ÓÒÚ-
ð˚È Û„ÓÎ Ò ÓÒ¸˛
Oz
, Ú‡ÍÓ‚˚:
22
1
(,)
cos
(,) (,)
pxy
pxy qxy
λ
−
=
++
;
22
1
(,)
cos
(,) (,)
qxy
pxy qxy
μ
−
=
++
;
22
1
1
cos
(,) (,)
pxy qxy
ν
=
+
+
.
ÑÎfl ÌÓðχÎË, Ëϲ˘ÂÈ ÔðÓÚË‚ÓÔÓÎÓÊÌÓ ̇Ôð‡‚ÎÂÌËÂ, ÔÓÎÛ˜ËÏ
ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ:
22
1
(,)
cos
(,) (,)
pxy
pxy qxy
λ
=
++
;
22
1
(,)
cos
(,) (,)
qxy
pxy qxy
μ
=
++
;
22
1
1
cos
(,) (,)
pxy qxy
ν
−
=
+
+
.
ê‡ÒÒÏÓÚðËÏ ÚÂÔÂð¸ ÔÓ‚ÂðıÌÓÒÚ¸
S , ð‡ÒÔÓÎÓÊÂÌÌÛ˛ ̇‰ ÔðÓÒÚÓÈ
ӷ·ÒÚ¸˛
D , ÎÂʇ˘ÂÈ ‚ ÔÎÓÒÍÓÒÚË xOy (ðËÒ. 1.1.12). ê‡ÁÓ·¸ÂÏ
ӷ·ÒÚ¸
D ÒÂÚ¸˛ ÔðÓÒÚ˚ı ÎËÌËÈ Ì‡ fl˜ÂÈÍË
1
D ,
2
D , ...,
n
D Ò ÔÎÓ-
˘‡‰flÏË
1
FΔ
,
2
FΔ
, ...,
n
F
Δ
;
λ
– ð‡Ì„ ‰ðÓ·ÎÂÌËfl D .
ê‡ÒÒÏÓÚðËÏ ˆËÎË̉ð˘ÂÒÍË ÔÓ‚ÂðıÌÓÒÚË, Ó·ð‡ÁÛ˛˘Ë ÍÓÚÓð˚ı
Ô‡ð‡ÎÎÂθÌ˚ ÓÒË
Oz , ‡ ̇Ôð‡‚Îfl˛˘ËÏË ÒÎÛÊËÚ ‰ðÓ·fl˘‡fl ÒÂÚ¸
ÎËÌËÈ Ó·Î‡ÒÚË
D
. ùÚË ˆËÎË̉ð˘ÂÒÍË ÔÓ‚ÂðıÌÓÒÚË ÔÂðÂÌÓÒflÚ
‰ðÓ·ÎÂÌË ËÁ ӷ·ÒÚË
D ̇ ÔÓ‚ÂðıÌÓÒÚ¸ S , ÍÓÚÓð‡fl ð‡Á·Ë‚‡ÂÚÒfl
Ú‡ÍËÏ Ó·ð‡ÁÓÏ Ì‡ fl˜ÂÈÍË
1
S ,
2
S , ...,
n
S . Ç˚·ÂðÂÏ ‚ ͇ʉÓÈ fl˜ÂÈÍÂ
k
S ÔðÓËÁ‚ÓθÌÛ˛ ÚÓ˜ÍÛ (,,)
kkkk
Mxyz Ë Ôðӂ‰ÂÏ ˜ÂðÂÁ Ì ͇҇-
ÚÂθÌÛ˛ ÔÎÓ˘‡‰ÍÛ
k
T ‰Ó ÔÂðÂÒ˜ÂÌËfl Ò ‚˚¯Â̇Á‚‡ÌÌ˚ÏË ˆËÎË̉-
20
ð˘ÂÒÍËÏË ÔÓ‚ÂðıÌÓÒÚflÏË. é·ÓÁ̇˜ËÏ ÔÎÓ˘‡‰¸ ͇҇ÚÂθÌÓÈ ÔÎÓ-
˘‡‰ÍË
k
T ˜ÂðÂÁ
k
SΔ .
ÖÒÎË ÒÛ˘ÂÒÚ‚ÛÂÚ ÍÓ̘Ì˚È Ôð‰ÂÎ
1
0
lim
n
k
n
k
SS
λ
→∞
=
→
=
Δ
∑
,
Ì Á‡‚ËÒfl˘ËÈ ÌË ÓÚ ÒÔÓÒÓ·‡ ‰ðÓ·ÎÂÌËfl, ÌË ÓÚ ‚˚·Óð‡ ÚÓ˜ÂÍ
k
M ̇
ÔÓ‚ÂðıÌÓÒÚË
S , ÚÓ ÓÌ Ì‡Á˚‚‡ÂÚÒfl ÔÎÓ˘‡‰¸˛ ÔÓ‚ÂðıÌÓÒÚË S , ð‡Ò-
ÔÓÎÓÊÂÌÌÓÈ Ì‡‰ ӷ·ÒÚ¸˛
D , ‡ ҇χ ÔÓ‚ÂðıÌÓÒÚ¸ ‚ ˝ÚÓÏ ÒÎÛ˜‡Â ̇-
Á˚‚‡ÂÚÒfl Í‚‡‰ðËðÛÂÏÓÈ.
êËÒ. 1.1.12
x
y
z
0
(,,)
kkkk
Mxyz
(,)
kk
xy
D
k
D
k
T
k
S
S
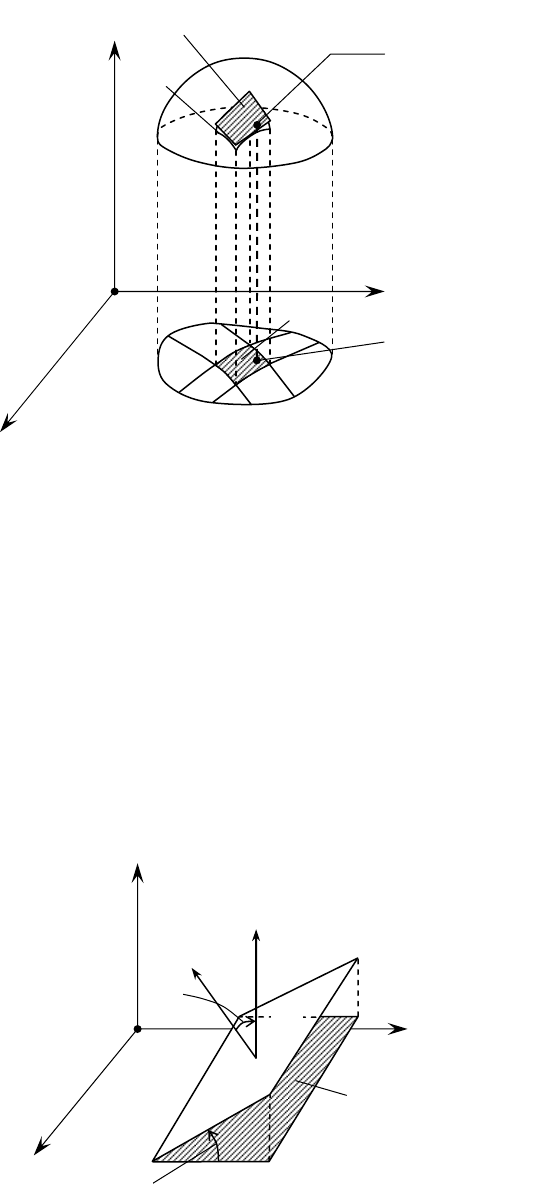
êËÒ. 1.1.13
x
y
z
0
N
u
ur
k
T
k
D
k
ϕ
k
ν
