Лобасова М.С. Тепломассообмен

Подождите немного. Документ загружается.

МОДУЛЬ 5. МАССООТДАЧА

Лекция 31. Тепло- и массообмен в двухкомпонентных средах. Основные положения тепло- и массообмена



Тепломассообмен. Курс лекций 251

div 0w





Уравнение движения (система уравнений Навье – Стокса):

Ddx





;

Ddy





;

Dw dp

Ddz





Уравнение массообмена:





Для неподвижной жидкости (

xyz

www





) уравнение массооб-

мена принимает вид





В последнем уравнении, называемом уравнением Фика, учтен перенос

массы только путем концентрационной диффузии. Это уравнение аналогично

дифференциальному уравнению теплопроводности при отсутствии внутрен-

них источников тепла. Если для температуры и массосодержания ввести

одинаковые обозначения, то уравнения по своему внешнему виду не будут

отличаться друг от друга. Сравнивая, можно видеть, что коэффициент диф-

фузии аналогичен коэффициенту температуропроводност

и.

Очевидно, если условия однозначности аналогичны, то все решения

дифференциального уравнения теплопроводности как для стационарного, так

и для нестационарного процессов могут быть использованы для расчета кон-

центрационной диффузии. В случае

D = a поля концентрации и температуры

подобны.

МОДУЛЬ 5. МАССООТДАЧА

Лекция 31. Тепло- и массообмен в двухкомпонентных средах. Основные положения тепло- и массообмена



Тепломассообмен. Курс лекций 252

1. Дайте определение следующих понятий: диффузия, концентрацион-

ная диффузия, молярная диффузия, молекулярная диффузия.

2. Какие явления называются эффект Дюфо и эффект Соре?

3. Укажите название закона, определяющего концентрационную диф-

фузию, и запишите его математическое выражение.

4. Дайте определение и запишите единицы измерения следующих фи-

зических величин: поток массы, плотность потока массы, местная концен-

трация, коэффициент молекулярной диффузии, коэффициент термодиффу-

зии, термодиффузи

онное отношение.

5. Дайте определение физических процессов: термодиффузия и баро-

диффузия.

6. Вследствие какого эффекта более тяжелые молекулы стремятся пе-

рейти в холодные области, если массы двух компонентов различны; а более

крупные переходят в холодные области, если массы молекул примерно оди-

наковы?

7. Вследствие ка

кого эффекта тяжелые молекулы стремятся перейти в

область повышенного давления, а легкие – наоборот?

8. За счет чего возникает бародиффузия?

9. В каком случае возникает термодиффузия?

10. Как изменяется поток массы и поток теплоты бинарной смеси при

наличии диффузионного переноса массы?

11. Запишите уравнение энергии для бинарной смеси диффундирую-

щих друг в друга компонентов.

12. Запишите уравнение массообмена в движущейся бинар

ной смеси.

13. Запишите уравнение движения для бинарной смеси.

14. Запишите уравнение неразрывности.

15. Сформулируйте закон Фика и запишите его математическое выра-

жение.

МОДУЛЬ 5. МАССООТДАЧА



Тепломассообмен. Курс лекций 253

Тепло- и массоотдача. Коэффициент массоотдачи. Стефанов поток.

Уравнение конвективной тепло- и массоотдачи. Уравнение теплового и

диффузионного пограничного слоев.

В движущейся однокомпонентной среде тепло переносится теплопро-

водностью и конвекцией. Этот процесс называется конвективным теплооб-

меном. По аналогии процесс совместного молекулярного и молярного пере-

носа вещества в движущейся многокомпонентной среде называют конвек-

тивным массообменом. При наличии массообмена процесс конвективного

теплообмена усложняется. Перенос тепла дополнительно осуществляется за

счет диффузии.

Практический интерес пред

ставляют процессы теплообмена и массо-

обмена при испарении, сублимации (возгонке), конденсации, сорбции, де-

сорбции и др. В этом случае система тел является гетерогенной. Под гетеро-

генной системой обычно понимают неоднородную систему, состоящую из

однородных частей, разделенных поверхностями раздела. Однородные части

гетерогенной системы должны иметь размеры, достаточно большие по срав-

нению с молекулами или средним расстоянием между ними. При этом мик-

роскопическ

ая неоднородность не принимается во внимание. Поверхность

жидкой (или твердой) фазы в этом случае играет роль, аналогичную роли

твердой стенки в процессах теплоотдачи без сопутствующей диффузии. На-

пример, при испарении жидкости образующийся пар переносится путем

диффузии в окружающую парогазовую смесь и одновременно имеет мест

теплопередача между парогазовой смесью и поверхностью жидкости.

Аналогично теплоотдаче конвективный массообмен между жидкостью

или твердой поверхностью и окружающей средой называют массоотдачей.

В рассматриваемых случаях тепло- и массоотдача идут одновременно.

Для практических расчетов теплоотдачи используют закон Ньютона-Рихмана

c ж

()qtt



  .

Для практических расчетов массоотдачи используют уравнение

()j



  

, (32.1)

МОДУЛЬ 5. МАССООТДАЧА

Лекция 32. Тепло- и массоотдача в двухкомпонентных средах



Тепломассообмен. Курс лекций 254

где



– коэфицент массоотдачи, отнесенный к разности концентраций диф-

фундирующего вещества;



– концентрация диффундирующего вещества на

жидкой (твердой) поверхности раздела фаз;



– концентрация диффунди-

рующего вещества вдали от жидкой (твердой) поверхности раздела фаз.

Используя уравнение состояния идеального газа, уравнение (32.1

)

можно записать в следующем виде:

()



  . (32.2)

Здесь

 – коэфицент массоотдачи, отнесенный к разности парциальных дав-

лений

рр  , где

– парциальное давление диффундирующего веще-

ства на жидкой (твердой) поверхности;

– парциальное давление этого же

компонента вдали от поверхности раздела фаз. Это уравнение впервые было

получено Э.Дальтоном (1788 г.)

Из уравнения (32.2

) следует, что

c0 c0

()

dJ j

pdFp p

 





Тождество следует рассматривать как определение коэфицента массо-

отдачи, отнесенного к разности парциальных давлений.

Коэфиценты



 связаны соотношением



 .

Рассмотрим процесс испарения жидкости в парогазовую среду. Будем

полагать, что полное давление по всему объему парогазовой смеси неизмен-

но, а температурные разности пренебрежимо малы. В этом случае можно

не учитывать термо- и бародиффузию.

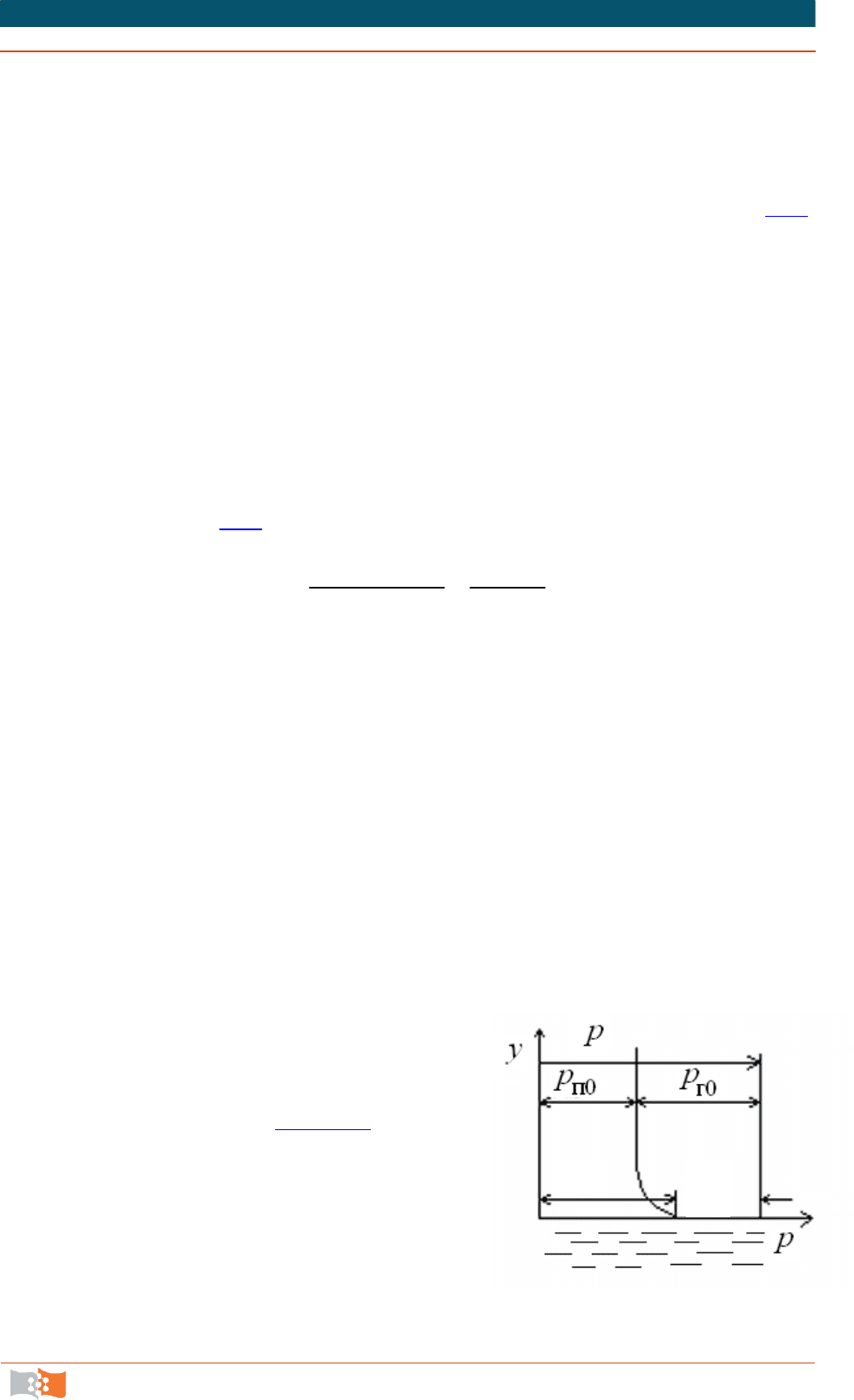
Парциальное давление пара изменяет-

ся от значения

п.с

на поверхности испа-

ряющейся жидкости до значения

п0

вдали

от поверхности раздела (рис. 32.1

). Парци-

альное давление газа

сп

рр



 также

должно изменяться в соответствии с изме-

нением парциального давления пара. При

constр 

градиенты парциального давления

и газа будут равны по абсолютной величине

и противоположно направлены:

Рис. 32.1

п.с

г.с

МОДУЛЬ 5. МАССООТДАЧА

Лекция 32. Тепло- и массоотдача в двухкомпонентных средах



Тепломассообмен. Курс лекций 255

гп







. (32.3)

Следовательно, газ должен диффундировать в направлении, противо-

положном направлению диффундирования пара. Пар может свободно диф-

фундировать в парогазовую среду. Для газа же поверхность жидкости явля-

ется непроницаемой преградой. Вследствие этого количество газа у поверх-

ности жидкости должно непрерывно увеличиваться. В случае стационарного

режима должно иметь место постоянство во времени распределения парци-

альных давлений пара и газа. Поэтому перемещение газа к поверхности ис-

парения должно компен

сироваться конвективным потоком парогазовой сме-

си, направленным от жидкости в парогазовую среду. Этот поток называют

стефановым потоком. Его скорость обозначим

с.п

Суммарный поток пара будет равен сумме молекулярного и конвек-

тивного потоков:

п.сп пс.п















. (32.4)

Суммарный поток газа у поверхности жидкости равен нулю:

г.сг пс.п

jD w







  







. (32.5)

Из уравнения (32.5

) с учетом (32.3) и

212







получим:

пп

с.п

гг

R Р





  







Подставив полученное значение

с.п

в уравнение (32.4), получим:

пг п п

п.сп п

гг

сс

рр

РР Р Р Р

jD D

Ру Ру

 

 

   

 



 

(32.6)

Это уравнение впервые было получено Стефаном. Оно отличается от

закона диффузии

к.д

i р







, относящегося к условиям беспрепятствен-

ного распространения обоих компонентов смеси, дополнительным множите-

МОДУЛЬ 5. МАССООТДАЧА

Лекция 32. Тепло- и массоотдача в двухкомпонентных средах



Тепломассообмен. Курс лекций 256

лем

р . Этот множитель учитывает конвективный (стефанов) поток, вы-

званный непроницаемостью поверхности испарения для газа. Как следует из

изложенного, стефанов конвективный поток появляется и при отсутствии

вынужденной или свободной тепловой конвекции.

Поток массы на поверхности испарения определяется с помощью урав-

нения (32.5

). Этот же поток может быть определен уравнением (32.6), в кото-

ром градиент парциального давления пара и парциальное давление газа бе-

рутся на поверхности жидкости. Приравняем правые части и получим:

п.сп0 п

()

рр

рр D





 







или

гс п

п.сп0

(/ )

рр

ру





 







. (32.7)

Уравнение (32.7

) по аналогии с уравнением







 







можно

назвать дифференциальным уравнением массоотдачи.

Рассмотренный процесс испарения жидкости в парогазовую смесь со-

ответствует условиям полупроницаемой поверхности, т.е. поверхности, про-

ницаемой для одного (активного) компонента смеси (пара) и непроницаемой

для другого (инертного) компонента (газа). Полупроницаемая поверхность

наблюдается при конденсации пара из парогазовой смеси.

В случае полностью проницаемой поверхности через нее проходят оба

компонента. Последнее, на

пример, имеет место при некоторых химических

реакциях на поверхности тела. Поверхность является полностью проницае-

мой и при конденсации обоих компонентов бинарной паровой смеси. Такой

же эффект может иметь место и при испарении некоторых растворов.

При наличии массообмена непосредственно на границе раздела фаз

имеется нормальная сост

авляющая скорости испаряющегося или конденси-

рующегося компонента (пара)

п.с

.п,с

п.с

w 



Эта скорость является условной величиной, она вызвана молекулярной

диффузией и стефановым потоком непосредственно в пристеночном слое.

МОДУЛЬ 5. МАССООТДАЧА

Лекция 32. Тепло- и массоотдача в двухкомпонентных средах



Тепломассообмен. Курс лекций 257

Общее количество тепла q , отдаваемого или воспринимаемого жидко-

стью и парогазовой смесью, равно сумме тепла



, переданного конвектив-

ным теплообменом, и тепла



, переносимого диффундирующей массой

в виде энтальпии.

При полупроницаемой поверхности в условиях стационарного процес-

са стефанов поток компенсирует встречный молекулярный поток газа и ре-

ально возникает лишь поперечный поток пара. В этом случае

с c п.сп.с

()qqq t ji



 

Общее количество тепла

может распределяться между





по-

разному.

По определению

c ж c ж

()

tt tt





   



, здесь то же, но тем не ме-

нее наличие поперечного потока массы

приводит к тому, что величина ко-

эфицента теплоотдачи  может быть иной, чем при теплоотдаче без массо-

обмена.

Из ряда теоретических работ следуют выводы: поток вещества направ-

ленный перпендикулярно поверхности от поверхности (испарение, сублима-

ция, десорбция, вдувание газа через пористую стенку) приводит к увеличе-

нию толщины пограничного слоя, при этом grad

w (вдоль поверхности)

уменьшается, отсюда коэфицент теплоотдачи уменьшается. В противопо-

ложном случае, когда поток вещества направлен перпендикулярно поверхно-

сти к поверхности (конденсация, сорбция, отсос газа), величина погранично-

го слоя уменьшается, grad

w увеличивается и коэффициент теплоотдачи

увеличивается.

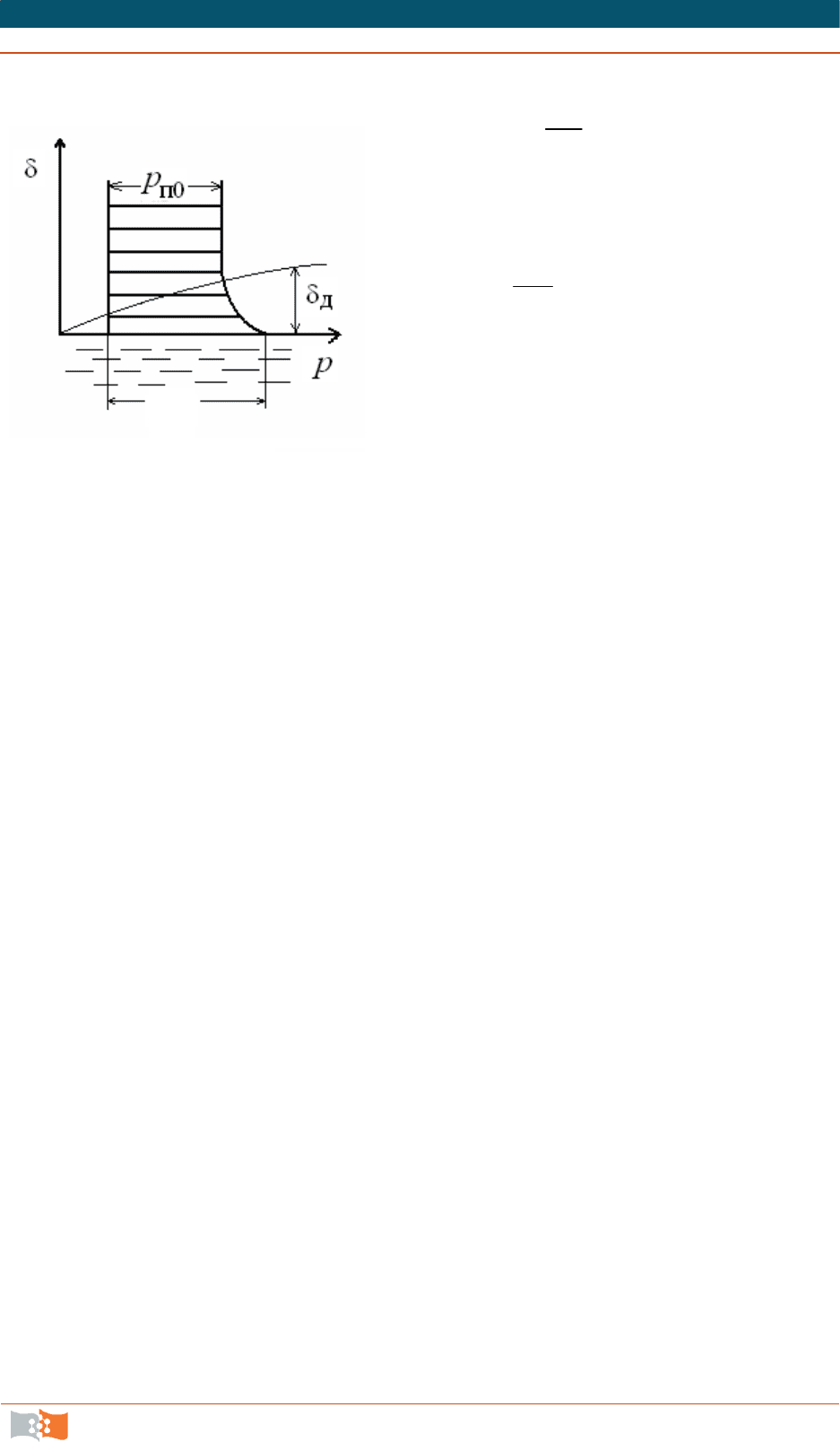
При омывании поверхности испарения движущейся парогазовой сме-

сью около испаряющейся поверхности помимо газодинамического и темпе-

ратурного пограничных слоев образуется диффузионный пограничный слой

(рис. 32.2

). В пределах диффузионного пограничного слоя парциальное дав-

ление пара изменяется от

п.с

на поверхности испарения до

п0

на внешней

границе пограничного слоя.

МОДУЛЬ 5. МАССООТДАЧА

Лекция 32. Тепло- и массоотдача в двухкомпонентных средах



Тепломассообмен. Курс лекций 258

Внутри пограничного слоя справед-

ливо условие







; вне пограничного

слоя и на его внешней границе выполня-

ются условия:







пп0

р

Таким образом, все изменения пар-

циального давления пара сосредотачива-

ются в сравнительно тонком слое, непо-

средственно прилегающем к поверхности

испаряющегося тела.

Диффузионный пограничный слой образуется и в процессах сублима-

ции, при конденсации пара из парогазовой смеси в процессах сорбции и др.

Как показывают теоретические расчеты пограничного слоя, коэффици-

енты массоотдачи качеств

енно зависят от направления и величины попереч-

ного потока массы так же, как и коэффициенты теплоотдачи.

1. Дайте определение понятий конвективный массообмен, массоотдача.

2. Перечислите процессы при которых одновременно происходит теп-

ло- и массообмен.

3. Дайте определение и запишите единицы измерения коэффициентов

массоотдачи, отнесенного к разности концентраций диффундирующего ве-

щества и к разности парциальных давлений.

4. Какое явление называют «Стефанов поток»?

5. Запишите уравнение Стефана. Чем оно отличается от за

кона Фика?

6. Запишите уравнение массоотдачи. Каким уравнениям оно аналогично?

7. Дайте определение диффузионного пограничного слоя.

8. В каком случае тепловой, гидродинамический и диффузионный по-

граничные слои будут иметь одинаковую толщину?

Рис. 32.2

п.с

МОДУЛЬ 5. МАССООТДАЧА



Тепломассообмен. Курс лекций 259

Аналогия переноса импульса, энергии и массы компонента (тройная

аналогия). Расчет массоотдачи в случае ламинарного пограничного слоя при

вынужденном движении. Расчет массоотдачи при турбулентном течении

жидкости на основе уравнений теплоотдачи.

(

)

Процессы переноса тепла и массы, обусловленные микроскопическими

механизмами, могут протекать в любой материальной среде, как в жидкости

или в газе, так и в твердых телах. Однако в первом случае эти процессы, как

правило, сопровождаются конвективным переносом. В твердых непрозрач-

ных телах единственным механизмом переноса тепла является теплопровод-

ность, а переноса массы – диффузия. Заметим, что термин молекулярная теп-

лопроводность (диффузия) являет

ся условным, так как материальными носи-

телями могут являться не только молекулы, но и атомы, ионы, а в случае те-

плопроводности – свободные электроны (в металлах) [25

Однако независимо от вида носителя, т.е. от механизма переноса, мож-

но дать единое описание всем этим процессам.

Логично предположить, что процесс переноса тепла теплопроводно-

стью происходит тем интенсивнее, чем резче изменяется температура,

т. е. чем больше градиент температуры. На этом предположении основан за-

кон Фурье, который удовлетворительно, как показывают эксперименты, опи-

сывает различные п

роцессы теплопроводности:

grad.qT







(33.1)

В соответствии с этим законом вектор плотности теплового потока



пропорционален по модулю градиенту температуры и направлен в сторону

убывания температуры. Коэффициент пропорциональности

λ называется ко-

эффициентом теплопроводности. Он является физическим параметром веще-

ства, характеризует его способность проводить тепло и зависит от темпера-

туры, а для газов также и от давления.

Если ввести обозначение

а c





, где ρ – плотность, кг/м

; с

– изо-

барная теплоемкость вещества, Дж/кг·К, и считать, что плотность и теплоем-

кость – постоянные величины, то выражение закона Фурье можно предста-

вить в виде

МОДУЛЬ 5. МАССООТДАЧА

Лекция 33. Тройная аналогия



Тепломассообмен. Курс лекций 260

grad,qa i







(33.2)

где i=ρc

T – объемная энтальпия, Дж/м

, т.е количество тепла, содержащееся

в единице объема вещества с температурой T. В такой формулировке закон

Фурье означает, что плотность теплового потока пропорциональна градиенту

объемной энтальпии. Коэффициент пропорциональности a носит название

коэффициента температуропроводности и является характеристикой интен-

сивности молекулярного переноса тепла. Величины, являющиеся, подобно

коэффициентам кинематической вязкости и температуропроводности, харак-

теристиками пер

еноса, часто называют коэффициентами переноса. Но если

кинематическая вязкость ν является коэффициентом переноса количества

движения, то температуро проводность представляет собой коэффициент пе-

реноса тепла.

Для процесса молекулярной диффузии аналогом закона Фурье является

закон Фика, определяющий диффузионный поток массы i-го компонента

смеси (если пренебречь термодиффузией):

gradρ



 . (33.3)

Отметим, что закон Фика полностью аналогичен закону Фурье в форме

(33.2

). Действительно, как следует из выражения (33.3), плотность диффузи-

онного потока массы пропорциональна по модулю объемной плотности мас-

сосодержания (т.е. парциальной плотности), а направление этого потока про-

тивоположно направлению градиента парциальной плотности. Коэффициент

диффузии D измеряется в тех же единицах (м

/с) и имеет тот же смысл, что и

коэффициент температуропроводности a (а также кинематической вязкости ν),

т. е. он характеризует интенсивность процесса молекулярной диффузии

и является поэтому коэффициентом молекулярного переноса массы.

Если плотность смеси ρ величина постоянная (что возможно, например,

для бинарной смеси при малых концентрациях примеси либо при близости

молекулярных мас

с примеси и основного вещества), учитывая, что парци-

альная плотность ρ

выражается через концентрацию (массовую долю) i-го

компонента как





получим закон Фика в виде

ρ grad .



 (33.4)

Эта формулировка закона Фика аналогична закону Фурье в форме

(33.1

Коэффициент диффузии зависит от природы веществ, составляющих

смесь, температуры и давления (для газов); слабой зависимостью коэффици-

ента диффузии от концентраций компонентов смеси в инженерных расчетах,

как правило, пренебрегают.