Малхорта, Нэреш К. Маркетинговые исследования. Практическое руководство

Подождите немного. Документ загружается.

£(Х,

А:

) = (10 -

9,33)

+ (12 -

9,33)

+ (12 -

9,33)

+ (4 -

9,33)

/-1

+ (12 -

9,33)

+ (6 -

9,33)

+ (8 -

9,33)

+ (2 -

9,33)

+ (18 -

9,33)

+ (9 -

9,33)

+ (17 -

9,33)

+ (2 -

9,33)

= 0,4489 +

1289

28,4089+

+ 7,1289 + 11,0889 + 1,7689 + 53,7289+

75,

1689

+ 0,1089 + 58,8289 + 53,7289 = 304,6668

£(Г,

-У) =

6,58)

+ (9 -

6,58)

+ (8 -

6,58)

+ (3 -

6,58)

i-i

+(10

6,58)

+ (4 -

6,58)

+ (5 -

6,58)

+ (2 -

6,58)

+ (11

6,58)

+ (9 -

6,58)

+ (10 -

6,58)

+ (2 -

6,58)

= 0,3364 + 5,8564 + 2,0164 + 12,8164+

1,6964

+ 6,6564 + 2,4964 + 20,9764 +

+ 19,5364 + 5,8564 +

1,6964

+ 20,9764 = 120,9168

Таким образом

=0.936.

^(304,6668X120,9168)

В этом примере

= 0,9361, что близко к 1. Это означает, что отношение респондента к сво-

ему городу сильно зависит от времени проживания в нем. Более того,

положительный

знак

указывает на прямую связь

(прямопропорциональную):

чем дольше респондент проживает в

городе, тем больше он ему нравится, и наоборот.

Так как

коэффициент

корреляции показывает меру, в которой вариация значений одной

переменной зависит от вариации другой, то

можно выразить через разложение полной вариа-

ции

(см. главу 16). Другими словами,

объяснимое изменение

= --

полная вариация

_SS,

_ полная вариация - вариация

ошибки

полная вариация

Следовательно,

г*

показывает, какая доля вариации одной переменной обусловлена вариа-

цией другой. И г, и

являются симметричными показателями связи между переменными.

Иначе говоря, корреляция между

Хм

Хта

же, что и корреляция между

Уи

X. Корреляция не за-

висит

оттого,

какая из переменных взята в качестве зависимой, а какая в качестве независи-

мой. Коэффициент корреляции является мерой линейной зависимости, и он не предназначен

для измерения силы связи в случае нелинейной зависимости. Таким образом,

= 0 просто оз-

начает отсутствие линейной зависимости между X и Y. Это не означает, что

А"

и У не взаимо-

связаны. Между ними может существовать нелинейная зависимость, которую нельзя опреде-

лить с помощью коэффициента корреляции

(рис.

17.1).

Если коэффициент корреляции вычисляют не для выборки, а для всей генеральной сово-

купности, то он обозначается греческой буквой р (ро). Коэффициент

— это оценка р. Обрати-

те внимание, что расчет

предполагает, что X и

У—

метрические переменные, кривые распре-

деления которых имеют одинаковую форму. Если эти

допущения

не удовлетворяются, то зна-

чение

уменьшается и р получается недооцененным. В маркетинговых исследованиях данные,

полученные с использованием относительной шкалы при небольшом числе категорий, могут

не быть строго интервальными. Это приведет к снижению

и недооценке р [3].

644 Часть III. Сбор, подготовка и анализ данных

-3

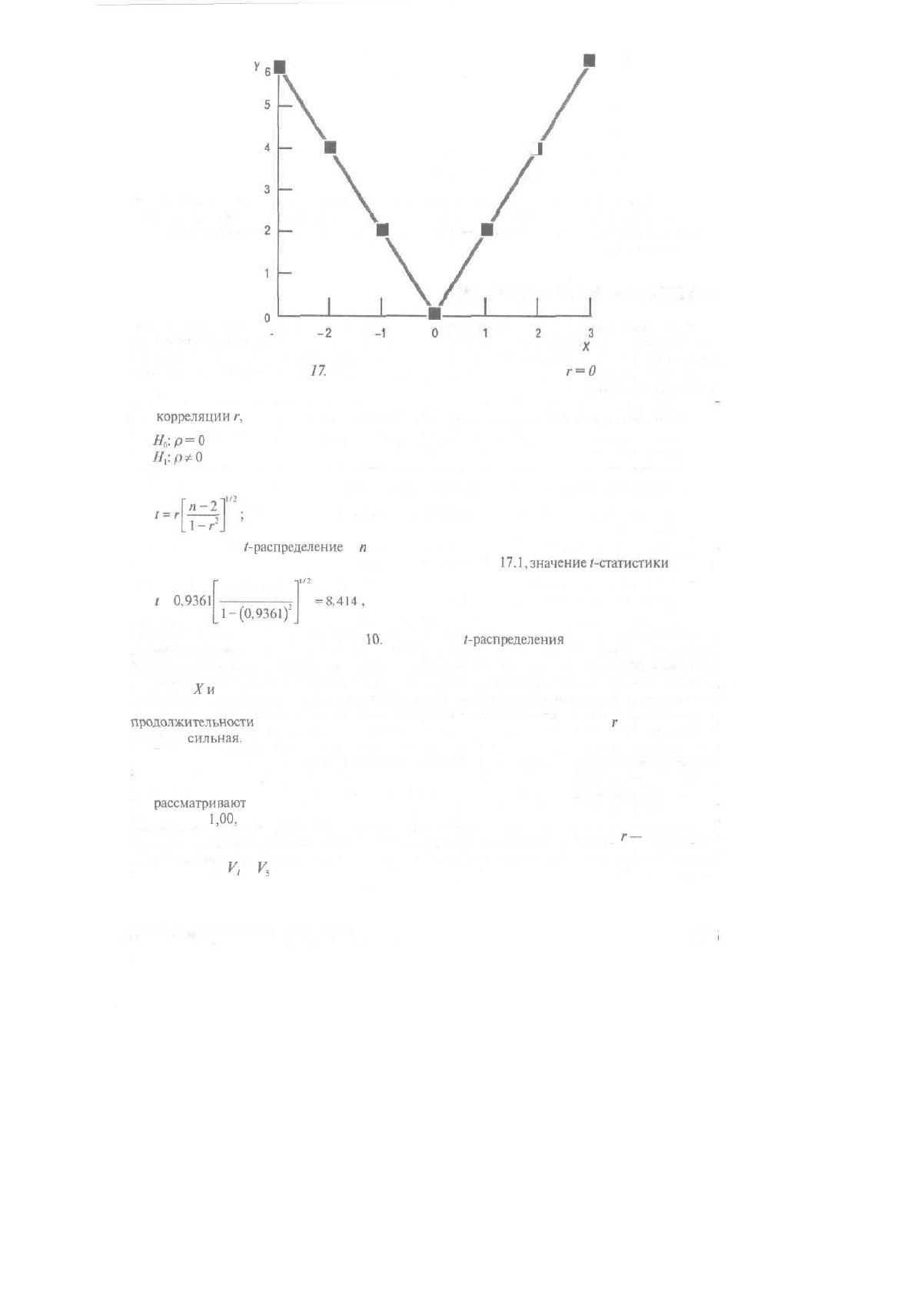
Рис.

17.

1. Нелинейная зависимость, для которой

г~0

Статистическую значимость связи между двумя переменными, измеренную коэффициен

том

корреляции

г,

можно легко проверить. Гипотезы имеют такой вид:

Статистику, лежащую в основе критерия для проверки гипотезы, вычисляют по формуле:

п-2

\-г

которая имеет

/-распределение

— 2 степенями свободы [4]. Для коэффициента корреля-

ции, вычисленного на основе данных, приведенных в табл.

17.1,

значение/-статистики

равно:

= 0.9361

12-2

1-(0,9361)

а число степеней свободы — 12 — 2 =

10.

Из таблицы

/-распределения

(табл. 4 Статистического

приложения) критическое значение t-статистики для двусторонней проверки и уровне значи-

мости а = 0,05 равно 2,228. Следовательно, нулевую гипотезу об отсутствии связи между пере-

менными

Хи

У отклоняют. Это наряду с положительным знаком коэффициента корреляции

показывает, что отношение респондента к своему городу прямо пропорционально зависит от

продолжительности

проживания его в городе. Более того, высокое значение

показывает, что

эта связь

сильная.

При выполнении многомерного анализа данных часто полезно изучить простую корреля-

цию между каждой парой переменных. Эти результаты представляют в форме корреляционной

матрицы, которая показывает коэффициент корреляции между каждой парой данных. Обыч-

но,

рассматривают

только самую нижнюю треугольную часть матрицы. Все элементы по диаго-

нали равны

1,00,

так как переменная коррелирует сама с собой. Верхняя треугольная часть мат-

рицы — зеркальное отражение нижней треугольной части матрицы, поскольку

г—

симметрич-

ный показатель связи между переменными. Форма корреляционной матрицы для пяти

переменных от

до

представлена ниже:

Глава 17. Корреляция и регрессия

645

0,5

0,3 0,4

0,1 0,3

0,6

0,2 0,5

0,3

0,7

Хотя

матрица

простых коэффициентов корреляций позволяет уяснить суть попарных свя-

зей, иногда исследователю хочется изучить связи между двумя переменными при условии

управления одной или несколькими переменными. В последнем случае следует оценивать ча-

стную

корреляцию.

ЧАСТНАЯ КОРРЕЛЯЦИЯ

В то время как линейный

коэффициент

корреляции — это показатель силы связи,

описывающий

линейную зависимость между двумя переменными, частный коэффициент

корреляции

(partial

correlation coefficient) — это мера зависимости между двумя перемен-

ными при фиксированных (исключенных) или скорректированных эффектах одной или

нескольких переменных.

Частный коэффициент корреляции (partial correlation coefficient)

Мера зависимости между двумя переменными после фиксации (исключения, корректиров-

ки) эффектов одной или нескольких переменных.

Эта статистика позволяет ответить на следующие вопросы,

• Зависит ли объем продаж от расходов на рекламу, если фиксировать влияние цены

(исключить эффект цены)?

• Существует ли связь между долей рынка и количеством торгового персонала, если за-

фиксировать эффект от усилий по продвижению товара?

• Связано ли восприятие качества товаров потребителями с их восприятием цены, если

исключить эффект торговой марки?

Предположим, что в этих ситуациях исследователь хочет вычислить силу связи между X и

Y, исключив при этом эффект влияния третьей переменной Z. Поступая логично, сначала сле-

дует удалить эффект

Zn3

значения переменной X. Для этого следует использовать коэффици-

ент парной корреляции

между X и Z, и вычислить значения X, исходя из информации о Z.

Затем полученное значение X вычитают из фактического значения X, получая скорректирован-

ное значение X. Аналогично корректируют значения Y, чтобы исключить эффект, и скорректи-

рованный коэффициент обозначают

г^..

Статистически, поскольку простой коэффициент кор-

реляции между двумя переменными полностью описывает линейную зависимость между ни-

ми, частный коэффициент корреляции можно вычислить, зная только эти простые

коэффициенты корреляции и не используя отдельные наблюдения.

Предположим, что исследователь хочет рассчитать силу связи между отношением к городу,

переменная Y, и продолжительностью проживания в нем, переменная

Х„

фиксируя при этом

эффект третьей переменной, а именно, погодных условий, переменная

Эти данные приве-

дены втабл. 17.1.

646 Часть

III.

Сбор, подготовка и анализ

данных

Линейные

коэффициенты

корреляции между переменными равны:

ТЖ|

=0,9361,

=0,7334,

1]Л

=0,5495

Частный коэффициент корреляции можно вычислить по формуле:

0,9361-(0,5495)(0,7334)

V •

=0,9386

^1-(0,5495)'

/1-(0,7334)

Результаты показывают, что исключение эффекта, связанного с погодными условиями,

незначительно воздействует на зависимость между отношением к городу и продолжительно-

стью проживания в нем.

Частные коэффициенты корреляции характеризуются так называемом порядком, который

указывает количество переменных, на которые необходимо внести поправку или которые сле-

дует проконтролировать (исключить). Простой коэффициент корреляции

имеет нулевой по-

рядок, поскольку отсутствует необходимость исключать дополнительные переменные при оп-

ределении силы связи между двумя переменными. Коэффициент

г^

представляет

собой част-

ный

коэффициент

корреляции первого порядка, так как при его расчете контролируют эффект

от влияния одной дополнительной переменной Z, частный коэффициент корреляции второго

порядка контролирует эффект от влияния двух переменных и т.д. Коэффициенты корреляции

более высокого порядка вычисляют аналогично. Частный коэффициент корреляции (я +

/)-го

порядка можно вычислить, поставив простые коэффициенты корреляции справа в предшест-

вующем уравнении для коэффициентов

л-го

порядка.

Частные коэффициенты корреляции могут оказаться полезными для выявления ложных

связей (см, главу 15). Связь

между

А'и

/является

ложной, если

А'связана

с Z, которая в дей-

ствительности является предиктором (независимой переменной) для Y. В этом случае корре-

ляция между X и Y исчезнет, если контролировать эффект от влияния переменной Z Рас-

смотрим пример, в котором потребление фирменного сухого завтрака (С) положительно

связано

с доходом

(У),

г„

= 0,28. Поскольку цена на этот товар вполне доступная, то марке-

тологи не ожидали, что доход окажется значимым фактором. Поэтому исследователь подоз-

ревает, что эта связь ложная. Результаты выборочного исследования также показали, что до-

ход позитивно связан с размером семьи

(Н),

коэффициент корреляции равен

= 0,48, а

размер семьи связан с потреблением сухого завтрака, коэффициент корреляции равен

0,56. Эти цифры свидетельствуют, что действительным предиктором потребления сухого

завтрака является не доход, а размер семьи.

Чтобы проверить это утверждение, маркетологи вычислили коэффициент частной корре-

ляции первого порядка между потреблением сухого завтрака и доходом, проконтролировав эф-

фект размера семьи. Читатель может проверить, что коэффициент частной корреляции равен

clll

0,02,

и первоначально обнаруженная корреляция между потреблением сухого завтрака и

доходом исчезла, когда мы исключили влияние размера семьи. Следовательно, корреляция

между доходом и потреблением сухого завтрака ложная. Специальный случай, когда частная

корреляция оказывается больше, соответствующей корреляции нулевого порядка, обусловлен

эффектом экранирования (см. главу 15) [5].

Другим

представляющим

интерес коэффициентом корреляции является частичный коэф-

фициент корреляции (part correlation coefficient). Он представляет корреляцию между

X, ко-

гда линейные эффекты других независимых переменных исключены из X, но не из Y.

Частичный коэффициент корреляции (part correlation coefficient)

Мера зависимости между Y и X, когда линейные эффекты других независимых переменных

исключены

из

X (но не из

Y).

Частичный коэффициент корреляции

y(3S}

вычисляют по формуле:

У(Х1|

=—

Глава 17. Корреляция и регрессия 647

Частичный

коэффициент

зависимости отношения к городу от продолжительности

прожи-

вания в нем при исключении эффекта погодных условий из переменной, обозначающей про-

должительность проживания, можно вычислить

следующим

образом:

0,9361-(0,5495){0,7334)

0,63806

Л.-*!

••*:

Частный коэффициент корреляции считают более важным, чем частичный коэффи-

циент корреляции. Парный коэффициент корреляции, частичный и частный предпола-

гают, что данные измерены с помощью интервальной или относительной шкал. Если

данные не соответствуют этим требованиям, то исследователь должен использовать не-

метрическую корреляцию.

ПРИМЕР. Реклама и предпочтения покупателей

Реклама играет важную роль в формировании у потребителей отношений и предпочте-

ний к торговым маркам. Маркетологи обнаружили, что для товаров, продажа которых про-

исходит с минимальным участием продавца, отношение покупателя к рекламе служит про-

межуточным звеном между распознованием торговой марки и отношением к ней. Что про-

изойдет с влиянием этой промежуточной переменной, если товары покупают дома

непосредственно через специализированную компьютерную сеть? Компания Ноте Shopping

Budapest в Венгрии исследовала воздействие рекламы на покупки. Маркетологи провели оп-

рос, в ходе которого измерили ряд показателей: отношение к товару, отношение к торговой

марке, отношение к рекламе, доверие к торговой марке и т.д. Была

выдвинута

гипотеза, со-

гласно которой при покупке через специализированную компьютерную сеть главным обра-

зом реклама определяет отношение к торговой марке. Чтобы установить степень связи от-

ношения к рекламе с отношением к торговой марке и доверием к ней, следовало вычислить

частный коэффициент корреляции. Для этого вычислялся частный коэффициент корреля-

ции

между

отношением к торговой марке и доверием к ней с одновременным исключением

влияния отношения к

рекламе.

Если отношение к рекламе высокозначимое, то частный ко-

эффициент корреляции должен быть значительно меньше, чем парный коэффициент кор-

реляции между доверием к торговой марке и отношением к ней. Исследование подтвердило

данную гипотезу. Затем компания

Saatchi

разработала радиорекламу для Ноте

Shopping

Budapest, чтобы выработать позитивное отношение к рекламе, и это стало главным

оружием в конкурентной борьбе [6].

НЕМЕТРИЧЕСКАЯ КОРРЕЛЯЦИЯ

Иногда маркетологу необходимо вычислить коэффициент корреляции между двумя немет-

рическими переменными.

Вспомним,

что неметрические переменные нельзя измерить с по-

мошью

интервальной или относительной шкалы и они не подчиняются закону нормального

распределения. Если мы имеем дело с порядковыми и числовыми неметрическими перемен-

ными, то для изучения связи между ними можно использовать два показателя неметрической

корреляции

(nonmetric

correlation): коэффициент ранговой корреляции Спирмена

д.

(Spearmen

rho

)

и коэффициент ранговой корреляции

Кендалла

(Kendall's

tau т).

Коэффициент неметрической корреляци (nonmetric correlation)

Показатель

корреляции

для

двух неметрических переменных, в котором используются ранги

переменных.

Для вычисления обоих коэффициентов используют ранги, а не абсолютные значения пе-

ременных, и подход,

лежащий

в основе их применения, совершенно одинаков. Оба коэффи-

циента изменяются в диапазоне

от—1

до+1

(см. главу

15).

648 Часть III. Сбор, подготовка и анализ данных

При отсутствии связанных рангов значение коэффициента ранговой корреляции Спирме-

на

р,

значительно ближе к коэффициенту парной корреляции Пирсона р, чем коэффициента

ранговой корреляции

Кендалла

т. В этих случаях абсолютное значение г стремится стать мень-

ше, чем р Пирсона. С другой стороны, если данные содержат большое количество связанных

рангов, то коэффициент г больше подходит для вычисления

корреляции.

В качестве эмпири-

ческого правила стоит запомнить, что коэффициент ранговой корреляции Кендалла целесооб-

разно использовать, когда большинство наблюдений попадает в относительно небольшое число

категорий (что приводит к большому количеству связанных рангов). И наоборот, целесообраз-

но использовать коэффициент ранговой корреляции Спирмена, когда мы имеем относительно

большое число категорий (что приводит к небольшому количеству совпадающих рангов) [7].

Парная корреляция, так же как частный и частичный коэффициенты корреляции, состав-

ляют концептуальную основу для парного и множественного регрессионного анализа.

РЕГРЕССИОННЫЙ АНАЛИЗ

Регрессионный анализ (regression analysis) — это мощный и гибкий метод установления

формы и изучения связей между метрической зависимой переменной и одной или нескольки-

ми независимыми переменными.

Регрессионный анализ (regression

analysis)

Статистический метод установления формы и

изучения

связей между метрической зависи-

мой переменной и одной или несколькими независимыми переменными.

Регрессионный анализ используют

следующих случаях.

1. Действительно ли независимые переменные обуславливают значимую вариацию зависи-

мой переменной; действительно ли эти переменные

взаимосвязаны?

2. В какой степени

вариацию

зависимой переменной можно объяснить независимыми пере-

менными: теснота связи?

3. Определить форму связи: математическое уравнение, описывающее зависимость между за-

висимой и независимой переменными.

4. Предсказать значения зависимой переменной.

5. Контролировать другие независимые переменные при определении вкладов конкретной

переменной.

Хотя независимые переменные могут объяснять вариацию зависимой переменной, это не-

обязательно подразумевает причинную связь. Использование в регрессионном анализе таких

терминов, как зависимая или критериальная переменная и независимая переменная

(предиктор) отражает наличие математической зависимости между переменными. Данная тер-

минология не подразумевает существование причинно-следственной

связи

между перемен-

ными. Регрессионный анализ имеет дело с природой и степенью связи между переменными и

не

предполагает,

что между ними существует какая-либо причинная связь. Вначале мы обсу-

дим парную регрессию, а затем множественную.

ПАРНАЯ РЕГРЕССИЯ

Парная регрессия (bivariate regression) — это метод установления математической (в форме

уравнения) зависимости между одной метрической зависимой (критериальной) переменной и

одной метрической независимой переменной (предиктором). Во многом этот анализ аналоги-

чен определению простой корреляции между двумя переменными. Однако для того чтобы вы-

вести уравнение, мы должны одну переменную представить как зависимую, а другую — как

независимую.

Глава

17. Корреляция и регрессия

649

Парная регрессия (bivariate

regression)

Метод установления математической (в форме уравнения) зависимости между двумя мет-

рическими

перемнными:

зависимой и независимой.

Примеры, приведенные ранее при изучении простой корреляции, рассмотрим с точки зре-

ния регрессии.

• Можно ли вариацию в объеме продаж объяснить расходами на рекламу? Какова форма

этой зависимости и можно ли ее выразить в виде

уравнения,

описывающего прямую

линию?

• Зависит ли вариация доли рынка от количества торгового персонала?

• Определяется ли отношение потребителей к качеству товара их отношением к цене на

этот товар?

Прежде чем обсудить процедуру выполнения двумерной регрессии, определим основные

статистики.

СТАТИСТИКИ,

СВЯЗАННЫЕ С ПАРНЫМ

РЕГРЕССИОННЫМ АНАЛИЗОМ

Ниже приведены статистики и термины,

относящиеся

к парному регрессионному анализу,

Модель парной

регрессии.

Основное уравнение регрессии имеет вид

;

/ЗД

где

Y~ зависимая или критериальная

переменная,

X—

независимая переменная, или

предиктор,

—

точка пересечения прямой регрессии с осью OY;

;

— тангенс угла наклона прямой и

е,

—

остаточный член (остаток), связанный с

/-м

наблюдением, характеризующий отклонение от

функции

регрессии

Коэффициент

детерминации.

Тесноту связи измеряют коэффициентом детерминации

Он

колеблется в диапазоне между 0 и 1 и указывает на долю полной вариации У, которая обуслов-

лена вариацией X.

Вычисляемое (теоретическое) значение Y. Вычисляемое значение

Уравно

= а +

Ьх,

где

— вычисляемое значение

У„

а параметры а и Ь — это вычисляемые оценки

0<,и

/^соответ-

ственно.

Коэффициент регрессии. Вычисляемый параметр Ъ обычно называют ненормированным ко-

эффициентом регрессии.

Диаграмма рассеяния (поле корреляции). Поле корреляции — это графическое представле-

ние точек с координатами, определяемыми значениями двух переменных

(независимой

и за-

висимой), для всех наблюдений.

Стандартная ошибка уравнения регрессии, Эта статистика SEE представляет собой стандарт-

ное отклонение фактических значений

Кот

теоретических значений У .

Стандартная

ошибка коэффициента регрессии Ь. Стандартное отклонение Ь, обозначаемое

называется стандартной ошибкой.

Нормированный коэффициент регрессии. Также называется бета-коэффициентом, или взве-

шенным

бета-коэффициентом. Показывает изменение У в зависимости от изменения X (угол

наклона прямой уравнения регрессии) при условии, что все данные нормированы.

Сумма квадратов ошибок. Значения расстояний всех точек до линии регрессии возводят в

квадрат и суммируют, получая сумму квадратов ошибок, которая является показателем общей

ошибки

В литературе этот

член

уравнения называют также

ошибочным

(ошибкой)

или

возмущающим

членом

(возмущением). — Прим. науч. ред.

650 Часть III. Сбор, подготовка и анализ данных

(-статистика,

/-статистику

с л — 2 степенями свободы можно использовать для проверки ну-

левой гипотезы, которая утверждает, что между X и

не существует линейной зависимости

или

Я„:

Р,

= 0, где

%.-.

ВЫПОЛНЕНИЕ ПАРНОГО РЕГРЕССИОННОГО

АНАЛИЗА

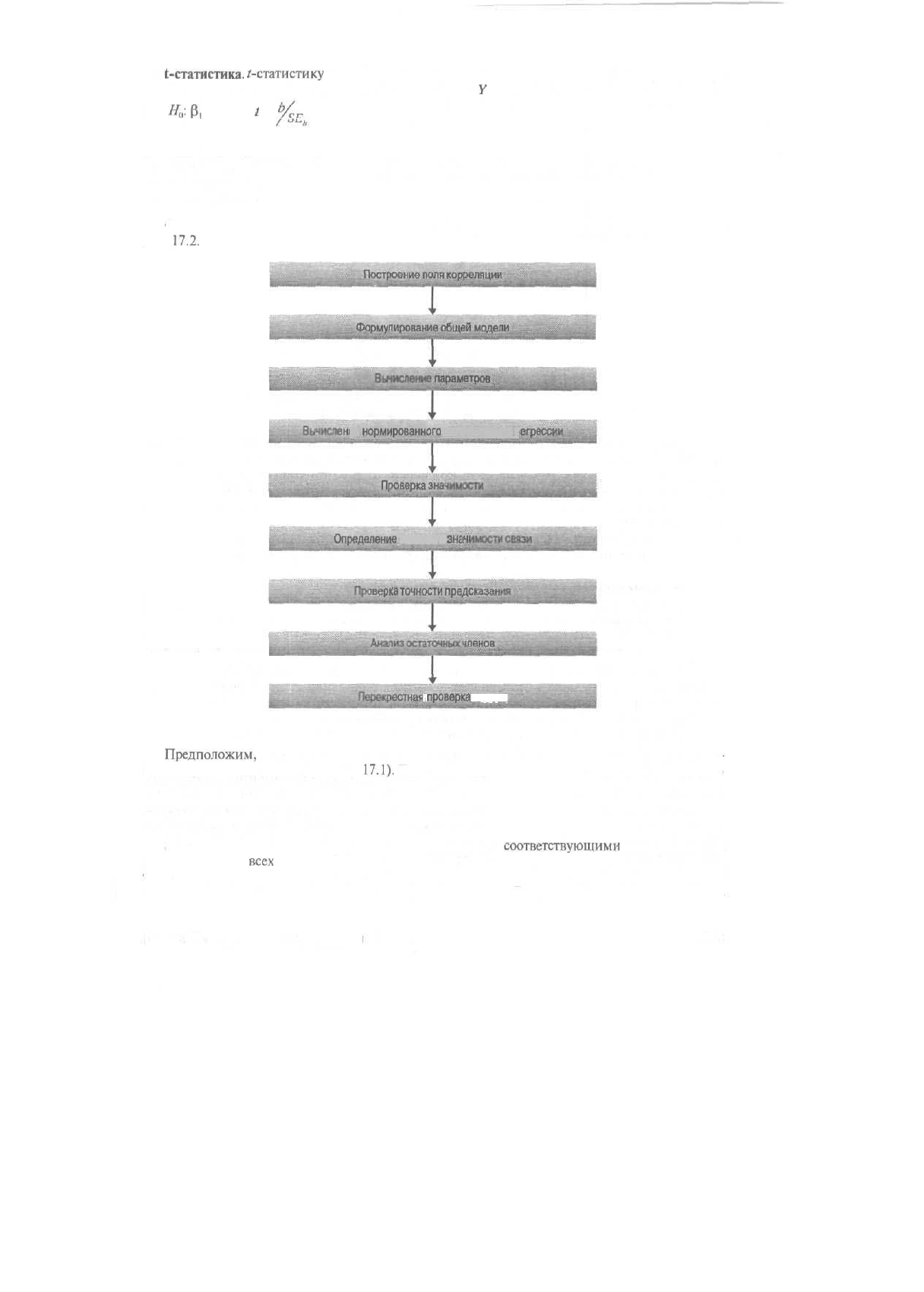
Стадии, из которых состоит процедура парного регрессионного анализа, приведены на

рис.

17.2.

да

нормированного

коэффициента р

Определение

тесноты

SHE

зга

точности

предок

проверка

модели

Рис. 17.2. Парный регрессионный анализ

Предположим,

что маркетолог хочет выяснить, зависит ли отношение к городу от длитель-

ности проживания в нем (см. табл.

17.1).

При выводе уравнения такой зависимости целесооб-

разно вначале изучить поле корреляции,

Поле корреляции

Это графическое изображение точек с координатами,

соответствующими

значениям двух

переменных для

всех

случаев. Обычно значения зависимой переменной откладывают по вер-

тикальной оси, в значения независимой — по горизонтальной. Поле корреляции используется

при определении формы зависимости между переменными, График дает исследователю первое

Глава 17. Корреляция и регрессия

651

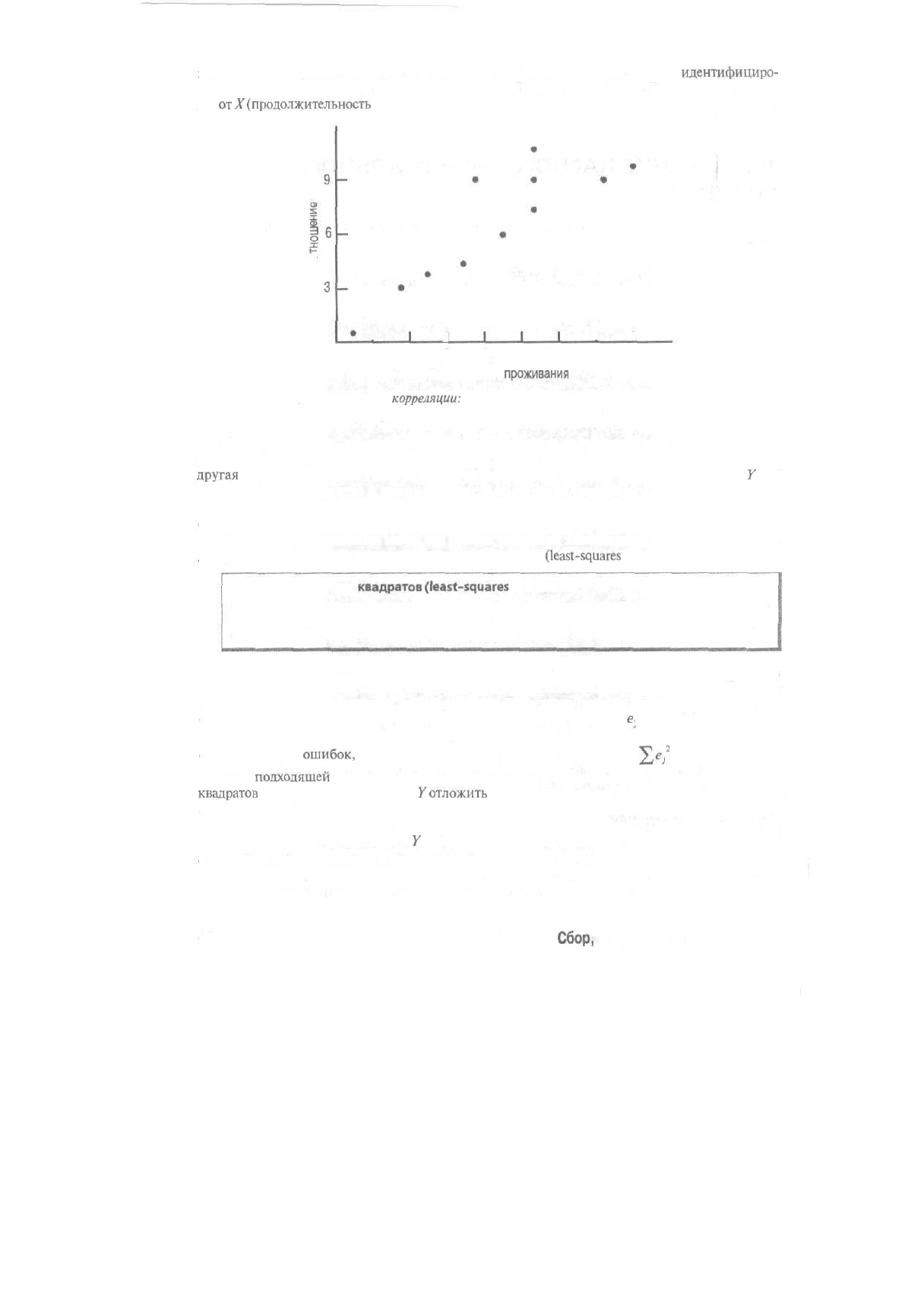
представление о форме данных и о возможных проблемах. На графике легко

идентифициро-

вать любую необычную комбинацию переменных. График зависимости У (отношение к горо-

ду)

от

^(продолжительность

проживания) дан на рис. 17.3.

2,25

4,5

6,75

11,25 13,5

Длительность

проживания

15,75

Рис. 17.3. Поле

корреляции:

отношение к городу в зависимости от

продолжительности проживания в нем

Из рисунка видно, что точки располагаются полосой от нижнего левого угла в верхний

правый. На графике можно увидеть форму зависимости: с ростом одной переменной

другая

переменная также увеличивается. Из рисунка видно, что зависимость между

и X

носит линейный характер и поэтому может быть описана уравнением прямой линии. Как

следует "подогнать" к этим точкам прямую линию, чтобы она наилучшим образом опи-

сывала данные?

Самый распространенный метод для расчета уравнения линейной регрессии по данным на

диаграмме рассеяния — это метод наименьших квадратов

(least-squares

procedure).

Метод наименьших

квадратов

(least-squares

procedure)

Метод, используемый для расчета параметров уравнения линейной регрессии, когда на ос-

нове поля корреляции минимизируются расстояния по вертикали всех точек поля от графи-

ка регрессии.

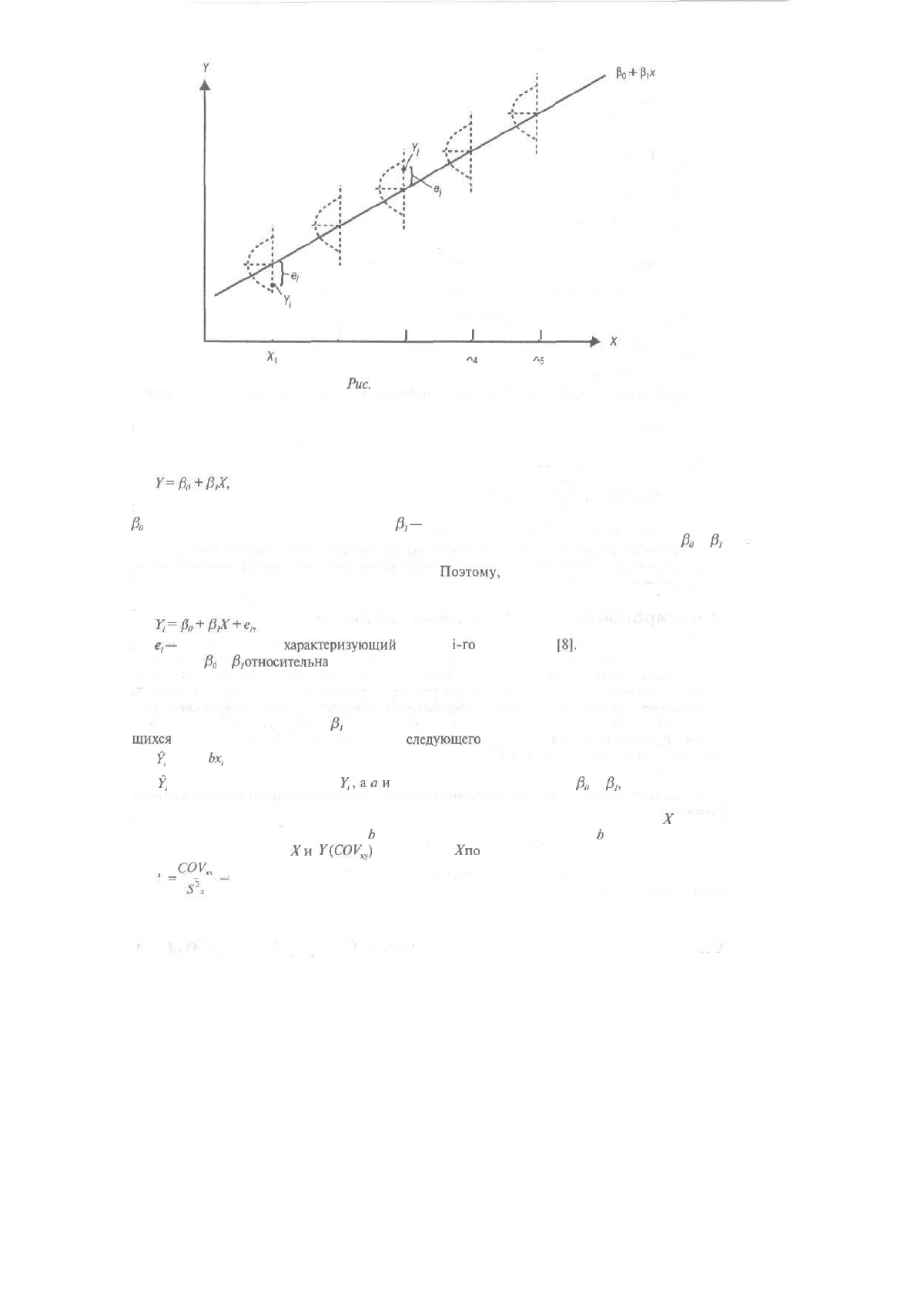
Методом наименьших квадратов определяют наиболее подходящую прямую регрессии,

минимизируя расстояния по вертикали всех точек поля корреляции от этой прямой. Наиболее

подходящая прямая называется линией регрессии. Если точка поля не лежит на линии регрес-

сии, то расстояние по вертикали от нее до линии называется ошибкой

е.

(рис. 17.4)

Расстояния от всех точек до линии регрессии возводят в квадрат и суммируют, получая

сумму квадратов

ошибок,

и это число показывает суммарную ошибку

^ef

. Для определения

наиболее

подходящей

линии с помощью метода наименьших квадратов минимизируют суммы

квадратов

ошибок. Если значения

Котложить

по вертикальной оси, а значения X— по гори-

зонтальной, как показано на рис. 17.4, то полученная аппроксимированная линия называется

регрессией У по X, так как расстояния по вертикали минимизированы. Поле корреляции по-

казывает, можно ли зависимость

по X выразить прямой линией и, следовательно, подходит

ли к этим данным парная регрессионная модель.

652

Часть III.

Сбор,

подготовка и анализ данных

х^

л'

I I

ill.

V Y Y V

"2 "3

Puc.

17.4. Парная регрессия

Модель парной регрессии

В модели парной регрессии форма прямой линии выражается уравнением:

где Y— зависимая, или критериальная переменная, X— независимая переменная, или предиктор,

Д,

— отрезок прямой, отсекаемый на оси OY,

—

угловой коэффициент (тангенс угла наклона).

Эта модель исходит из того, что У полностью определяется X. При известных значениях

Д,

можно предсказать значение Y. Однако в маркетинговом исследовании немного связей

между переменными четко детерминированы.

Поэтому,

чтобы учесть вероятностную при-

роду связи, в регрессионное уравнение вводят ошибочный член. Базовое уравнение рег-

рессии принимает вид:

где

е,~

член уравнения,

характеризующий

ошибку

1-го

наблюдения

[8].

Оценка регрессионных

параметров

Д,

относительна

проста.

Определение параметров уравнения регрессии

В большинстве случаев Д, и

ft,

неизвестны, и их определяют (оценивают), исходя из имею-

щихся

выборочных наблюдений с помощью

следующего

уравнения:

= а +

их,

где

— теоретическое значение

,аак

Ь — вычисленные значения

Д,

/3,,

соответственно,

Константу Ь обычно называют ненормированным коэффициентом регрессии. Он выражает

угол наклона линии регрессии и показывает ожидаемое изменение Г при изменении

А"

на еди-

ницу. Формулы для вычисления а и

просты [9]. Угловой коэффициент

можно вычислить

через ковариацию между

А"

Y(COV^)

и дисперсию

по

формуле:

COV^ _

---

Глава 17. Корреляция и регрессия

653