Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

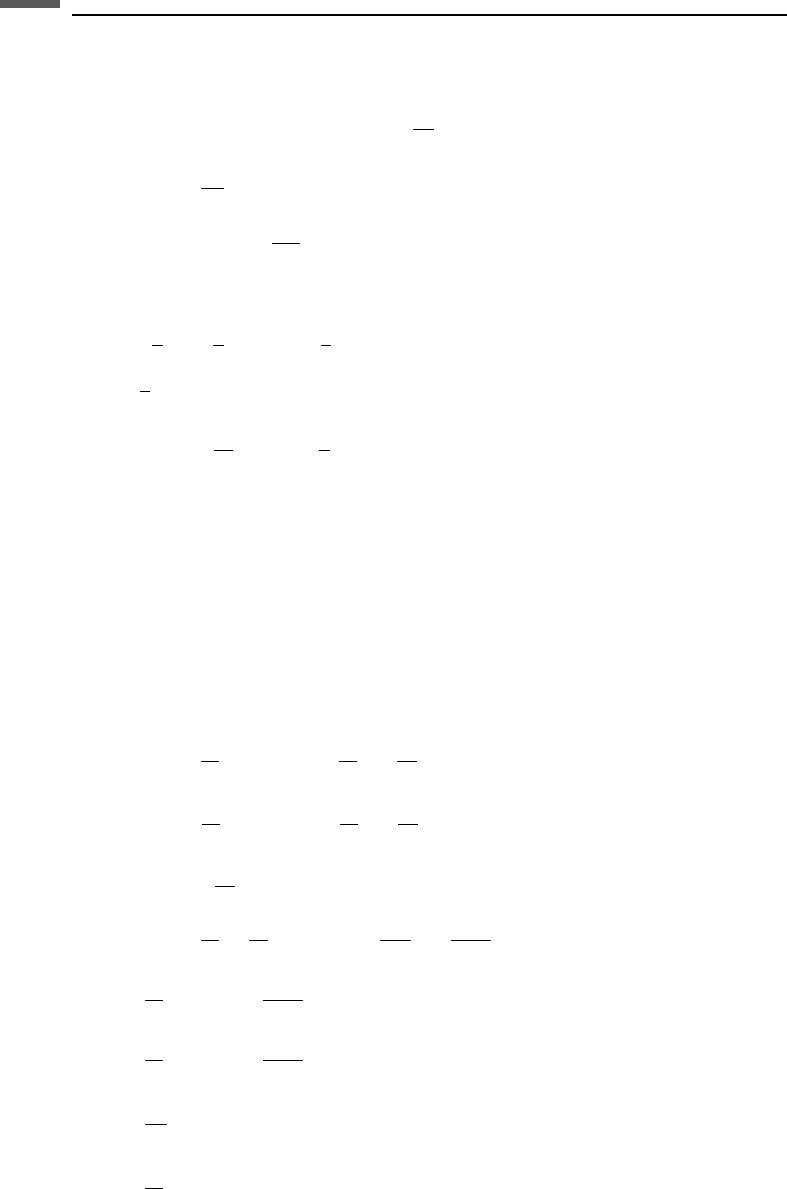
In the quasi-static limit the effective homogeneous poroelastic medium is itself

transversely anisotropic with effective constants given by (Gelinsky and Shapiro, 1997a):

B ¼ b

 f

1



þ f

1



1



1

C ¼ c

1



1

F ¼ c

1



1



D ¼ d

1



1

M ¼ m

P ¼ R



1



1





Q ¼ R

1



1

R ¼ r

1



1





1



1



1

The symbol 

indicates volumetric averages of the enclosed properties. When the

individual thin layers are transversely isotropic with a horizontal symmetry axis (x

the effective medium has orthorhombic symmetry and is described by the stiffness

tensor A

with nine independent constants and four additional Biot parameters,

, P

, and R. The layers themselves are characterized by the transversely

isotropic coefficients, b

, c

, f

, d

, and m

, (and a

¼2m

þb

), and three additional

poroelastic constants, p, q, and r, with x

as the symmetry axis instead of x

. The

effective constants are given by (Gelinsky and Shapiro, 1997a):

¼ c



1



1





¼ a



1



1





¼ a

1



1

¼ f



1



1





1



1



1



1



1



1

217 4.15 Poroelastic Backus average

¼hd

¼ R





1



1



¼ R





1



1



¼ R



1



1



R ¼







1



1

When the individual thin layers are isotropic, the effective constants for the equiva-

lent transversely isotropic homogeneous poroelastic medium can be expressed in

terms of averages of the Lame

constants l

and m

of the dry frame of the layers. For

isotropic layers, a

¼ a

¼ a ¼ 1  K

. In the quasi-static limit the effective

poroelastic constants are:

B ¼ 2

þ 2m



þ 2m



þ 2m



1

C ¼

þ 2m



1

F ¼

þ 2m



1

þ 2m



D ¼ m

1



1

M ¼ m

P ¼R 2

þ 2m



þ 2m



þ 2m



þ 2m



1

Q ¼R

þ 2m



þ 2m



1

R ¼ r

1



þ 2m





þ 2m



þ 2m



1

Uses

These equations can be used to model a finely stratified heterogeneous poroelastic

medium as an effective homogeneous anisotropic poroelastic medium.

Assumptions and limitations



All materials are linear and poroelastic.



Layer thicknesses are much smaller than the seismic wavelength. A rule of thumb is

that the wavelength must be at least ten times the layer thickness.

218 Effective elastic media: bounds and mixing laws

4.16 Seismic response to fractures

Synopsis

One approach to modeling the effects of fractures on the elastic properties of rocks is

to represent them as thin layers for which the elastic moduli are smaller (softer) than

those of the unfractured background rock. The soft fracture layer modulus represents

the extra compliance of the fracture relative to the background rock. When the

seismic wavelength is long compared with the layer thickness and fracture spacing,

then the overall elastic response of a parallel array of such fracture layers can be

estimated using the Backus (1962) average (Section 4.13) (Hudson et al., 1996;

Schoenberg, 1980; Schoenberg and Douma, 1988; Hudson and Liu, 1999).

If the thickness of the weak fracture layer is h, and the fracture layer P-wave

modulus and shear modulus are M

and m

, respectively, then the total normal and

shear displacements across the thin layer under normal and shear stresses, s

and s

,are

¼ 

h=M

¼ 

h= 2m

ðÞ:

The fracture normal and shear compliances, Z

and Z

, can be defined as

@

;

@

where Z

and Z

have units of (stress/length)

1

. By defining these fracture com-

pliances, then at long wavelengths the fracture layer can be thought of as a plane of

weakness, across which displacement discontinuities, d

and d

, occur when stress is

applied. Hence, these are often referred to as displacement discontinuity models.

Quasi-static fracture compliance

Both empirical and model-based methods have been applied to estimating values of

fracture compliance (and its reciprocal the fracture stiffness). Jaeger et al. (2007) give

an excellent summary. Myer (2000) represented joint deformation using the solution

for the deformation of coplanar two-dimensional elliptical cavities (Figure 4.16.1)

from Sneddon and Lowengrub (1969):

d

41 nðÞa

pm 1  rðÞ

ln sec

1  rðÞ

where m is the rock shear modulus, n is the Poisson ratio, r is the fractional area of

contact of the crack faces, a is the crack length, and b ¼a/(1 r) is the center-to-

center crack spacing. With this model, crack closure under stress can be modeled

using a distribution of crack aspect ratios, a, with a corresponding distribution of

closing stresses (Section 2.9 )





21 nðÞ

219 4.16 Seismic response to fractures

Hence, as normal compressive stress increases, a fraction of the cracks close, the

contact area grows, and the fracture stiffens. Delameter et al. (1974) solved the

related problem of the deformation of a doubly periodic array of cracks (Figure

4.16.2), which represents an extension of the Myer model to a set of parallel fractures.

Mavko and Nur (1978) modeled the deformation of two-dimensional nonelliptical

cracks (Figure 4.16.3). They showed that the deformation under infinitesimal incre-

ments of stress is identical to the deformation of an elliptical crack of the same length;

hence, the crack stiffness of the models in Figures 4.16.1 and 4.16.3 will be the same.

An important difference of the nonelliptical cracks is that under finite compressive

stress, the cracks shorten, leading to increased contact area and fracture stiffening.

Mavko and Nur also gave the solution for a nonelliptical crack that makes contact at a

midpoint (Figure 4.16.4) before closing.

Another set of theoretical models represents the fracture as a distribution of Hertzian

contacts (Section 5.4) of random heights (Greenwood and Williamson, 1966;White,

1983; Brown and Scholz, 1986; Jaeger et al., 2007).

Figure 4.16.1 Representation of a partially open fracture with coplanar two-dimensional

elliptical cracks.

Figure 4.16.2 Representation of parallel partially open fractures with a doubly periodic

array of two-dimensional elliptical cracks.

220 Effective elastic media: bounds and mixing laws

Based on laboratory measurements of joint closure, Goodman (1976) proposed an

empirical stress–displacement function



¼ 

1 þ

 d





; 0  d

< d

where s

is an initial reference stress at d

¼0, d

is the maximum possible closure,

and t is an empirical exponent. Bandis et al. (1983) proposed a simpler form



 d

leading to the fracture compliance

d

1 þ





where Z

is the compliance at zero stress.

Figure 4.16.4 Representation of a partially open fracture with nonelliptical two-dimensional

cracks that make multiple contacts under normal compression.

Figure 4.16.3 Representation of a partially open fracture with nonelliptical two-dimensional

cracks with tapered ends.

221 4.16 Seismic response to fractures

As discussed in Section 4.10, Hudson and Liu (1999) estimated the compliance of

rough joint faces in contact using two models. In one model they represent the

fracture as a planar distribution of small circular cracks with first-order normal and

shear compliances equal to



where g

is the number of cracks per unit area of the fracture plane, a is the crack

radius, r is the fraction of the fracture plane that is not in contact, and m is the

unfractured rock shear modulus. For dry cracks

16 l þ 2mðÞ

33l þ 4mðÞ

4 l þ 2mðÞ

3 l þ mðÞ

Hence for dry fractures,





dry

¼ 1 

where n is the Poisson ratio of the unfractured rock, or Z

n-dry

 Z

-dry

. For “weak”

inclusions (i.e., when ma=½K

 is of the order of 1 and is not small enough to be

neglected)

16ðl þ2mÞ

3ð3l þ4mÞ

ð1 þ MÞ

4ðl þ 2mÞ

3ðl þ mÞ

ð1 þ k Þ

where

M ¼

pam

ðl þ 2mÞ

ð3l þ 4mÞ

k ¼

½K

ðl þ 2mÞ

pamðl þ m Þ

and K

and m

are the bulk and shear modulus of the inclusion material. Hence, for

fluid-filled fractures (m

¼0)





wet





dry

1 þ k

1 þ M

In general, shear fracture compliance models depend very much on the amount

of shear displacement. Large shear displacement is thought to involve interference of

222 Effective elastic media: bounds and mixing laws

asperities on opposite fracture faces (Jaeger et al., 2007). At small normal stresses,

asperities might slide over one another, causing dilatancy in the fracture zone. At

larger normal stresses, asperities need to fail in either brittle or plastic fashion to

accommodate slip.

Infinitesimal shear deformation in the fault zone can be modeled analogously to the

normal deformation discussed above. Open cracks undergo shear deformation, while

welded or frictional contacts have zero slip. The two-dimensional models for normal

fracture deformation illustrated in Figures 4.16.1–4.16.4 can be scaled for shear

deformation. For example, using dislocation analysis (Section 2.9), both normal

and in-plane shear of two-dimensional cracks can be represented using edge disloca-

tions, and hence the normal and shear fracture stiffnesses are equal for dry fractures.

In general, a reasonable estimate of the infinitesimal shear compliance can be obtained

from the infinitesimal normal compliance using the Hudson and Liu expressions

for Z



/ Z

Dynamic response

The displacement discontinuity model has been applied to derive the dynamic

response of waves impinging on the fracture plane (Kendall and Tabor, 1971;

Schoenberg, 1980; Angel and Achenbach, 1985;Pyrak-Nolteet al., 1990). Schoenberg

(1980) gives expressions for the frequency-dependent P-wave reflection R(o) and

transmission T(o) coefficients for normal incidence:

RðoÞ¼

i$

1  i $

TðoÞ¼

1  i $

$ ¼

oZ



where $ is a dimensionless frequency, o is the angular frequency, r is the density,

is the P-wave velocity, and Z

is the infinitesimal fracture normal compliance.

R(o) and T(o) are frequency-dependent and complex. An excellent review is given

by Jaeger et al. (2007).

Use

The models presented here can be used to predict the effects of joints and fractures on

the static and dynamic elastic properties of rocks.

Assumptions and limitations

The models presented here assume that the unfractured rock mass is isotropic, linear,

and elastic. The joints and fractures are assumed to be planar.

223 4.16 Seismic response to fractures

4.17 Bound-filling models

Synopsis

The Voigt–Reuss (Section 4.2) and Hashin–Shtrikman–Walpole (see Section 4.1)

bounds yield precise limits on the maximum and minimum possible values for the

effective bulk and shear moduli of an isotropic, linear, elastic composite. Specifically,

for a mixture of two components, the Hashin–Shtrikman–Walpole bounds can be

written as

HS

¼ K

ðK

 K

1

þ f

ðK

1

ð4:17:1Þ

HS

¼ m

ðm

 m

1

þ f

þ8m

þ2m

hi

1

ð4:17:2Þ

where subscripts 1 and 2 refer to properties of the two components, having bulk

moduli, K

, K

, shear moduli, m

, m

, and volume fractions f

and f

. Most commonly,

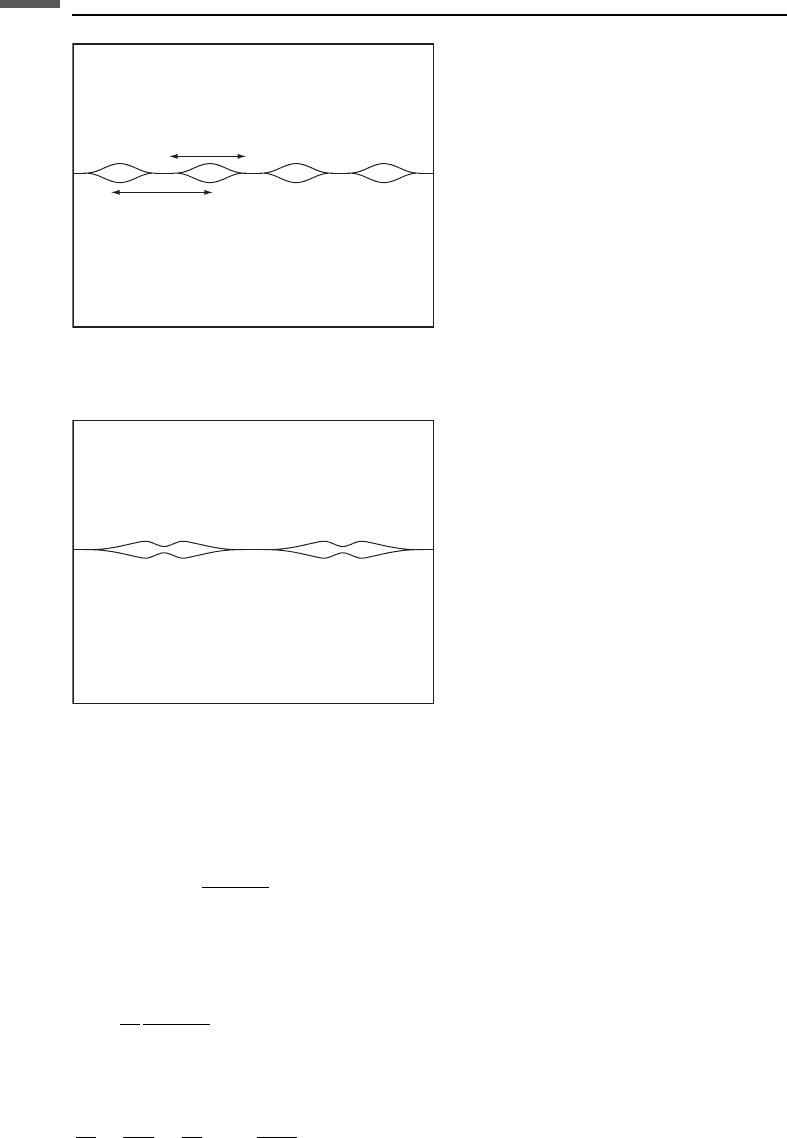
these bounds are applied to describe mixtures of mineral and pore fluid, as illustrated

in Figure 4.17.1. Equations (4.17.1) and (4.17.2) yield the upper bounds when K

and

are the maximum bulk and shear moduli of the individual constituents, and

the lower bounds when K

and m

are the minimum bulk and shear moduli of the

constituents, respectively. The maximum (minimum) shear modulus might come from

a different constituent from the maximum (minimum) bulk modulus. For example, this

would be the case for a mixture of calcite K ¼ 71 GPa; m ¼ 30 GPaðÞand quartz

K ¼ 37 GPa; m ¼ 45 GPaðÞ.

Note

Equations (4.17.1) and (4.17.2) simplify to the Hashin–Shtrikman bounds (Section

4.1) when one constituent has both the maximum bulk and shear moduli, while the

other constituent has the minimum bulk and shear moduli.

The modified Hashin–Shtrikman bounds use exactly the same equations shown

above. However, with modified bounds the constituent end members are selected

differently, such as a mineral mixed with a fluid–solid suspension (Figure 4.17.1)ora

stiffly packed sediment mixed with a fluid–solid suspension. The critical-porosity

model (Nur et al., 1991, 1995), described in Section 7.1, identifies a critical porosity,



, that separates load-bearing sediments at porosities <

and suspensions at

porosities >

. Modified Hashin–Shtrikman equations (or modified Voigt–Reuss

equations) can be constructed to describe mixtures of mineral with the unconsolidated

fluid–solid suspension at critical porosity. The modified upper Hashin–Shtrikman

curve has been observed empirically to be a useful trend line describing, for example,

224 Effective elastic media: bounds and mixing laws

how the elastic moduli of clean sandstones evolve from deposition through compaction

and cementation. The modified upper Hashin–Shtrikman curve, constructed as such,

is not a rigorous bound on the elastic properties of clean sand, although sandstone

moduli are almost always observed to lie on or below it.

The Voigt–Reuss–Hill average (Section 4.4) is an estimate of elastic modulus

defined to lie exactly half-way between the Voigt upper and Reuss lower bounds

(Figure 4.17.2). A similar estimate can be constructed to lie half-way between the

upper and lower Hashin–Shtrikman bounds (Figure 4.17.2). These two estimates have

little practical value, except in the case where the constituent end-members are

elastically similar, as with a mixture of minerals without pore space. In this latter

case, an average of upper and lower bounds yields a useful estimate of the average

mineral moduli.

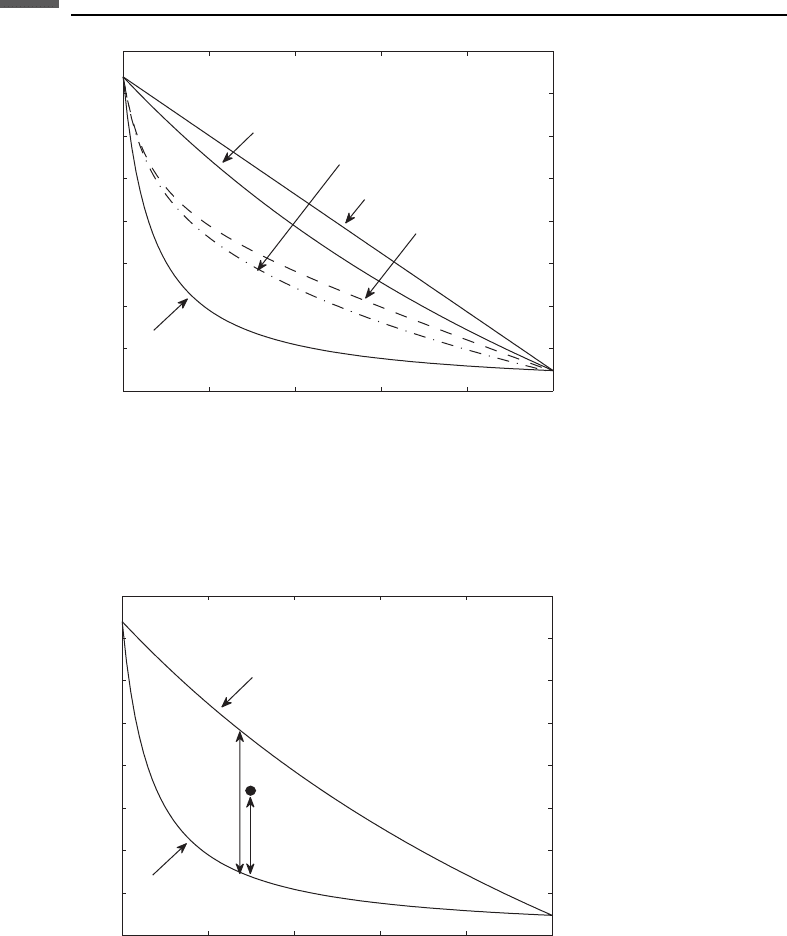
Marion’s (1990) bounding average method (BAM) of fluid substitution (Section

6.9) uses the position of porosity–modulus data between the bounds as an indication

of rock stiffness. In Figure 4.17.3, the Hashin–Shtrikman upper and lower bounds are

displayed for mixtures of mineral and water. The data point A lies a distance d above

the lower bound, while D is the spacing between the bounds at the same porosity.

In the bounding average method, it is assumed that the ratio d/D remains constant if

the pore fluid in the rock is changed, without changing the pore geometry or the

stiffness of the dry frame. Though not theoretically justified, the BAM method

sometimes gives a reasonable estimate of high-frequency fluid-substitution behavior.

Fabricius (2003) introduced the isoframe model to describe behavior between the

modified upper and lower Hashin–Shtrikman bounds. In this model, the modified

upper Hashin–Shtrikman curve is assumed to describe the trend of sediments that

0 0.2 0.4 0.6 0.8 1

Porosit

Bulk modulus (GPa)

Hashin–Shtrikman

upper bound

Hashin–Shtrikman

lower bound

Modified upper

Hashin–Shtrikman

bound

Critical porosity

Figure 4.17.1 Hashin–Shtrikman and modified Hashin–Shtrikman bounds for bulk modulus

in a quartz–water system.

225 4.17 Bound-filling models

become progressively more compacted and cemented as they trend away from the

lower Reuss average ( Figure 4.17.4) – an empirical result. It is assumed that these

rocks contain only grains that are load-bearing with good grain-to-grain contacts.

Sediments that fall below the modified upper bound are assumed to contain inclu-

sions of grain–fluid suspensions, in which the grains are not load-bearing. A family of

0 0.2 0.4 0.6 0.8 1

Porosity

Bulk modulus (GPa)

Hashin-Shtrikman

lower bound

Hashin–Shtrikman

upper bound

Figure 4.17.3 The bounding average method. It is assumed that the position of a data

point A, described as d/D relative to bounds, is a measure of the pore stiffness.

0 0.2 0.4 0.6 0.8 1

Porosity

Bulk modulus (GPa)

Hashin–Shtrikman

lower bound

Voigt

Voigt–Reuss–Hill

Hashin–Shtrikman

upper bound

Hashin–Shtrikman average

Figure 4.17.2 Hashin–Shtrikman and Voigt–Reuss bounds for bulk modulus in a quartz–

water system. The Voigt–Reuss–Hill curve is an average of the Voigt upper and Reuss lower

bounds. The Hashin–Shtrikman average curve is an average of the Hashin–Shtrikman upper and

lower bounds.

226 Effective elastic media: bounds and mixing laws