Майсеня Л.И. Математика в примерах и задачах. Часть 3
Подождите немного. Документ загружается.


196
Если функция f(x) имеет в некоторой окрестности точки
0
xx
=
производные до (
1
n
+
)-го порядка включительно, то при
0
xx
→
верна формула Тейлора:
2
0
0000
()
0
0
()
()()()()()...
2!
()
()(),
!
n
n
n
fx
fxfxfxxxxx
fx
xxRx
n
′′
′
=+−+−++
+−+
(17.21)
где
()
n
Rx
– остаточный член формулы Тейлора.
Существует несколько форм записи остаточного члена.
В частности, в форме Лагранжа:
(1)
1
0
()
()(),
(1)!
n
n
n
f
Rxxx
n
ξ
+
+
=−
+
0
(,).
xx
ξ
∈
Если в формуле Тейлора
0
0,
x
=
получим частный вид фор-
мулы Тейлора – формулу Маклорена:
()
2
(0)(0)(0)
()(0)...(),
1!2!!
n
n
n
fff
fxfxxxRx
n
′′′
=+++++
где
01.
θ
<<
Верны следующие формулы Маклорена:
2
1...(),
1!2!!
n
x
n
xxx
eRx
n
=+++++ (17.22)
где
1
(),01;
(1)!
n
x
n
x
Rxe
n
θ
θ
+
=<<
+
( )
35
1
sin...1(),
3!5!!
n
n
n
xxx
xxRx
n
−
=−+−+−+
где
1
()sin(1),
(1)!2
n
n
x
Rxxn
n
π
θ
+
=++
+
,
n
∈
N
01;
θ
<<
( )
24
cos1...1(),
2!4!!
n
n
n
xxx
xRx
n
=−+−+−+
(17.23)
где
1
()cos(1),
(1)!2
n
n
x
Rxxn
n
π
θ
+
=++
+
,
n
∈
N
01;
θ
<<
23
1
ln(1)...(1)(),
23
n
n
n
xxx
xxRx
n
+
+=−+−+−+
(17.24)
197
где
1
1
1
()(1),
(1)(1)
n
n
n
n
x
Rx
nxθ
+
+
+
=−
++
01;
θ
<<
2
(1)(1)...(1)
(1)1...(),
2!!
mn
n
mmmmmn
xmxxxRx
n
−−−+
+=+++++
где
11
(1)...()
()(1),
(1)!
mnn
n
mmmn
Rxxx
n
θ
−−+
−−
=+
+
01.
θ
<<
Формулы Маклорена могут быть использованы в прибли-
женных вычислениях. При этом абсолютная погрешность при-
ближения в случае чередования знаков в формуле Маклорена не
превосходит абсолютной величины первого отбрасываемого сла-
гаемого.
Пример 1. Вычислить предел функции с помощью правила Лопи-
таля:
1)
2
55
3
1
lim;
44
x
x
ee
x
→
−
−
2)
9
lim;
2
x
x
xx
→−∞
−+
+−
3)
2
lim(2)tg;
x
xx
π
π
→
−
4)
0
21
lim;
sin3tg3
x
xx
→
−
5)
( )
1
2
0
limcos2.
x
x
x
→
Решение. 1) Непосредственное вычисление предела дает неопре-
деленность вида
0
.
0
Поскольку условия теоремы 1 выполняются, ис-
пользуем правило Лопиталя. По формуле (17.19) имеем:
2222
2
555555
3332
1111
55
5
1
0()()10
limlimlimlim
0
44(44)(4)12
10105
lim.
12126
xxxx
xxxx
x
x
eeeeexe
xxxx
ee
e
x
→→→→
→
′′
−−
=====
′′
−−
===
2) Непосредственное вычисление предела дает неопределенность
вида
,
∞
∞
поэтому используем правило Лопиталя:
1
2
2(1)
2
9(9)
limlimlim
2(2)
1
21
limlim0.
2(22)(22)
xxx
xx
x
x
xx
xxxx
x
xxx
→−∞→−∞→−∞
→−∞→−∞
−
−
−
−
′
−+∞−+
====
∞
′
+−+−
+
−−−
===
−−−−−
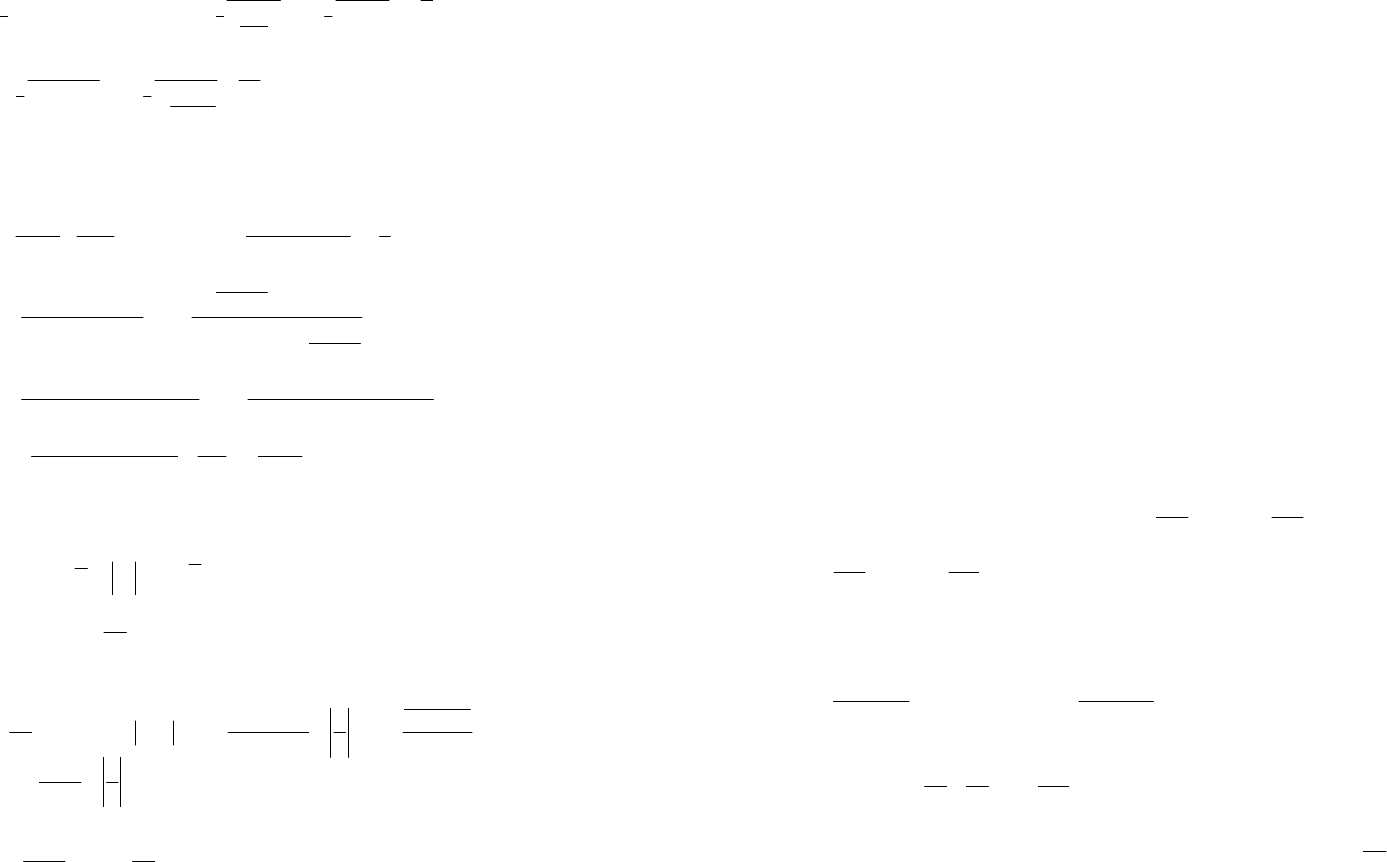
198
3) Имеем неопределенность вида
.0
∞
⋅
Поэтому, чтобы восполь-
зоваться правилом Лопиталя, преобразуем выражение, стоящее под
знаком предела:
222
22
2
1
tg
1
sin
220
lim(2)tg(0)limlim
ctg0
(2)22
limlim2.
(ctg)1
xxx
xx
x
x
xx
xx
x
x
x
πππ
ππ
ππ
π
π
→→→
→→
−−
−=⋅∞====
′
−
====−
′
−
−
4) Имеем неопределенность вида
.
∞−∞
Для того чтобы использо-
вать правило Лопиталя, преобразуем вначале выражение с помощью
формул тригонометрии:
00
2
00
2
33
3
00
23
cos3
3sin3
cos3
212tg3sin30
lim()lim
sin3tg3sin3tg30
3cos3
(2tg3sin3)
limlim
(sin3tg3)
3cos3tg3
63cos363cos3
limlim
3cos3tg33sin3
xx
xx
xx
x
x
x
xx
xxxx
x
xx
xx
xx
x
xxx
→→
→→
→→
⋅
−
−=∞−∞===
⋅
−
′
−
===
′
⋅
⋅+
−−
==
⋅+
( )
2
2
00
3sin3cos33sin3
131
3limlim.
32sin3
3sin3cos31
xx
x
xxx
x
xx
→→
=
⋅+
===∞
⋅
+
5) Так как приходим к неопределенности вида
1,
∞
то вначале пре-
образуем выражение, стоящее под знаком предела:
( )
1
1
2
2
0
limln(cos2)
0
limcos21.
x
x
x
x
x
xe
→
∞
→
==
Получили
2
0
1
limln(cos2),
x
x
x
→
неопределенность вида
0.
⋅∞
Преоб-
разовав выражение, используем правило Лопиталя:
22
000
0
2sin2
cos2
1ln(cos2)0
limln(cos2)0limlim
02
tg20
lim.
0
xxx
x
x
x
x
x
x
xx
x
x
→→→
→
−
=∞⋅====
=−=
Используем далее эквивалентность бесконечно малых:
00
tg22
limlim2.
xx
xx
xx
→→
−=−=−
199
Пример 2. Разложить многочлен
542
371
xxxx
−+++
по степени
х + 2.
Решение. Используем формулу (17.21). В данном случае
0
2.
x
=−
Тогда
542
(2)(2)3(2)(2)7(2)189.
f
−=−−−+−+−+=−
Найдем производные функции:
43
()51227;
fxxxx
′
=−++
32
()20362;
fxxx
′′
=−+
2
()6072;
fxxx
′′′
=−
(4)
()12072;
fxx=−
(5)
()120;
fx=
(6)
()0.
fx
=
Все производные порядка выше пятого равны нулю. Вычислив
значение полученных производных в точке х
0
= –2, получаем:
43
(2)52122227179;
f
′
−=⋅+⋅−⋅+=
32
(2)2023622302;
f
′′
−=−⋅−⋅+=−
2
(2)602722384;
f
′′′
−=⋅+⋅=
(4)
()120272312;
fx=−⋅−=−
(5)
()120.
fx=
Подставив найденные значения в формулу (17.21), получим:
54223
452
345
302384
37189179(2)(2)(2)
2!3!
312120
(2)(2)89179(2)151(2)
4!5!
64(2)13(2)(2).
xxxxxxx
xxxx
xxx
−+++=−++−+++−
−+++=−++−++
++−+++
Пример 3. Вычислить предел с помощью формул Маклорена:
1)
2
0
1
lim;
ln(12)
x
x
e
x
→
−
+
2)
3
2
0
1cos
lim.
2
x
x
xx
→
−
−
Решение. 1) Используем формулу Маклорена (17.22). Тогда
2
242
1
11...()1.
1!2!!
n
x
n
xxx
eRx
n
−=+++++−
Выражение в правой части равенства эквивалентно величине
2
1!
x

200
при
0,
x
→
так как остальные слагаемые имеют более высокий поря-
док малости («быстрее» стремятся к 0), т. е.
2
2
1~.
x
ex
−
По формуле (17.24) получаем:
23
2
(2)(2)
ln(12)2...()~2,
23
n
xx
xxRxx
+=−+++ если
0.
x
→
Тогда
2
2
00
10
limlim0.
ln(12)02
x
xx
ex
xx
→→
−
===
+
Заметим, что более рациональное решение этого примера возмож-
но с помощью таблицы эквивалентных бесконечно малых, так как ис-
пользование формул Маклорена выступает здесь как способ доказа-
тельства эквивалентностей.
2) Преобразуя выражение под знаком предела и используя форму-
лу (17.23), получим:
32
2
000
24
3
00
2!4!
1cos(1cos)(1coscos)31cos
limlimlim
(2)2
2
11...()
33
limlim...()0.
22224
xxx
n
n
xx
xx
xxxxx
xxx
xx
Rx
xx
Rx
x
→→→
→→
−−++−
===
−
−
−+−++
==−++=
Пример 4. Используя формулу Маклорена, вычислить прибли-
женное значение
ln1,2
с точностью 0,001.
Решение. Используем формулу (17.24):
234
11111
ln1,2ln(10,2)ln1...
55
253545
=+=+=−+−+
⋅⋅⋅
Поскольку знаки чередуются и
4
1
0,00040,001,
45
=<
⋅
то достаточно
взять три слагаемых.
Получаем
111
ln1,20,183.
550375
≈−+≈
Задания
I уровень
1.1. Вычислите предел с помощью правила Лопиталя:
1)
2
0
sin4
lim;
23
x
x
xx
→
−
2)
0
tg2
lim;
tg3
x
x
x
→
3)
2
0
lim;
arctg
x
xx
x
→
−
201
4)
3
0
82
lim;
x
x
x
→
−+
5)
3
2
0
lim;
2
x
x
xx
→
+
6)
0
lim.
sin
xx
x
ee
x
−
→
−
1.2. Используя формулу Тейлора, разложите многочлен P(x)
по степеням
():
xa
−
1)
32
()652,
Pxxxx
=+++
1;
a
=−
2)
32
()27139,
Pxxxx
=−+−
1;
a
=
3)
32
()439,
Pxxxx
=−++
2;
a
=
4)
32
()3225747,
Pxxxx=+++
2;
a
=−
5)
432
321,
yxxxx
=−−++−
2;
a
=−
6)
5432
232,
yxxxxx
=+−+−+
1.
a
=−
1.3. Используя известные формулы Маклорена, получите
формулу Маклорена для функции:
1)
2
sin;
yx
= 2)
sh3;
yx
=
3)
2
log3;
yx
=
4)
2
.
x
ye
=
II уровень
2.1. Вычислите предел функции с помощью правила Лопиталя:
1)
2
sin
0
31
lim;
lncos
x
x
x
→
−
2)
2
sin
2
1
lim;
x
x
e
x
→∞
−
3)
2
2
2
tg
lim;
log
x
x
x
x
π
→
−
4)
sin
32
5
31
lim;
ln(67)
x
x
xx
π
→
−
−+
5)
2
limln(61);
x
x
ex
−
→+∞
+
6)
0
limctg3ln(1);
x
xx
→
⋅+
7)
3
5
lim(3)ln;
x
x
x
x
→+∞
+
+
8)
1
0
limarctg52;
x
x
x
→+
⋅
9)
22
2
11
lim;
6832
x
xxxx
→
−
−+−+
10)
0
1
limln3.
arctg
x
x
x
→+
−
2.2. Используя формулу Тейлора, разложите функцию по
степеням
():
xa
−

202
1)
43
32,
yxxx
=++−
2;
a
=
2)
5432
2343,
yxxxxx
=+−−+−
1.
a
=
2.3. Используя формулу Маклорена, вычислите приближен-
но с указанной точностью
:
∆
1)
3
0,98,
0,0001;
∆=
2)
cos22,5,
°
0,001;
∆=
3)
3
log1,02,
0,0001;
∆=
4)
sin132,5,
°
0,001.
∆=
2.4. Разложите следующие функции по формуле Маклорена
до члена указанного порядка включительно:
1) ()
x
fxe
−
= до члена с
3
;
x
2)
2
2
()
xx
fxe
−
= до члена с
4
;
x
3)
()ln(sin)
fxx
=
до члена с
5
;
x
4)
()coscos
fxx
=
до члена с
2
.
x
III уровень
3.1. Вычислите предел функции с помощью правила Лопиталя:
1)
0
lim(sin2);
x
x
x
→
2)
sin3
0
1
lim;
x
x
x
→
3)
5
0
limarcsin;
2
x
x
x
→
4)
0
2
lim;
x
e
x
x
−
→
5)
3
ln(3)
2
2
0
84
lim;
35
xx
x
xx
xx
++
→
+−
−+
6)
( )
1
2
sin
32
0
lim1tg;
x
x
x
→
+
7)
( )
2
4
lnsin2
lim;
4x
x
x
π
π→ −
8)
2
1
11
lim.
1
43
x
x
xx
→
−
−
−+
3.2. Вычислите предел функции различными способами:
1)
0
cos6cos3
lim;
cos31
x
xx
x
→
−
−
2)
3
0
tg6sin3
lim;
xx
x
xx
ee
→
−
−
3)
3
0
sin3
lim;
ln(1)
x
xx
x
→
−
+
4)
5
0
log(1)
lim;
cos
x
x
xx
exx
→
+−
−−
203
5)
4
0
tg2sin3
lim;
x
xxx
x
→
+−
6)
2
0
2
lim;
xx
x
ee
x
−
→
+−
7)
2
/2
4
0
cos
lim;
x
x
xe
x
−
→
−
8)
( )
2
0
2
lncos
lim.
sin
x
x
x
xxx
→
+
−
3.3. Используя известные формулы Маклорена, разложите
функцию f(x) по степеням x (запишите первые 5 слагаемых):
1)
22
()sincos;
fxxx
= 2)
2
12
()ln;
1
x
fx
x
−
=
+
3)
5
2
()3216;
fxx
=+ 4)
44
()sincos.
fxxx
=−
17.6. Исследование функций. Наибольшее
и наименьшее значение функций на промежутке
Всюду далее функция f(x) определена на рассматриваемых
промежутках.
Теорема 1 (достаточное условие монотонности). Дифферен-
цируемая на (a, b) функция возрастает (убывает) на этом интер-
вале тогда и только тогда, когда
()0
fx
′
>
(()0)
fx
′
<
(,).
xab
∀∈
Точка х
0
называется точкой локального максимума (мини-
мума) функции f(x), если существует некоторая окрестность точ-
ки
0
x
такая, что для всех x из этой окрестности выполняется не-
равенство
0
()()
fxfx
≤
(
)
0
()().
fxfx
≥
Значение
0
()
fx
называется локальным максимумом (ми-
нимумом) функции.
Точки максимума или минимума функции называются точ-
ками экстремума (локального). Максимум и минимум называ-
ются экстремумом функции.
Теорема 2 (необходимое условие существования экстрему-
ма функции). Если в точке
0
x
функция f(x) достигает экстрему-
ма, то ее производная в этой точке равна нулю или не существует.
Те точки из области определения функции f(x), в которых
производная функции f(x) обращается в нуль или не существует,
204
называют критическими. Исследование функции на экстремум
начинается с нахождения критических точек. Однако не в каж-
дой критической точке существует экстремум. Для того чтобы
определить точки экстремума, используют достаточные условия
(признаки экстремума).
Теорема 3 (первый признак экстремума функции). Пусть
0
x
–
критическая точка непрерывной функции f(x). Если в некоторой
окрестности точки
0
x
выполняется условие
{
0
0
()0
для всех ,
()0
для всех ,
fxxx
fxxx
′
><
′
<>
то
0
x
– точка локального максимума;
если выполняется условие
{
0
0
()0
для всех ,
()0
для всех ,
fxxx
fxxx
′
<<
′
>>
то
0
x
– точка локального минимума.
Если производная
()
fx
′
имеет один и тот же знак в левой и
правой полуокрестности точки
0
,
x
то
0
x
не является точкой
экстремума.
Теорема 4 (второй признак экстремума функции). Пусть
0
x
–
критическая точка дважды дифференцируемой функции f(x). То-
гда
0
x
является точкой локального минимума функции f(x), если
0
()0,
fx
′′
>
и точкой локального максимума, если
0
()0.
fx
′′
<
Теорема 5 (третий признак экстремума функции). Пусть
f(x) – n раз непрерывно дифференцируемая в критической точке
0
x
функция и
(1)
000
()()...()0,
n
fxfxfx
−
′′′
====
()
0
()0.
n
fx
≠
Тогда:
1) если n – четное и
()
0
()0,
n
fx
<
то
0
x
– точка локального
максимума;
2) если n – четное и
()
0
()0,
n
fx
>
то
0
x
– точка локального
минимума;
3) если n – нечетное, то
0
x
не является точкой локального
экстремума.
З а м е ч а н и е 1. При исследовании функции и построении ее
графика целесообразно использовать первый признак экстремума, так
как одновременно получаем возможность исследования функции на
монотонность.
205
Точка
0
x
называется точкой глобального максимума (ми-
нимума) функции f(x) на некотором промежутке, если для лю-
бой точки x из этого промежутка выполняется неравенство
0
()()
fxfx
≤
(
)
0
()().
fxfx
≥
Точки глобального максимума и минимума называются
точками глобального экстремума. Значения функции в этих
точках называются соответственно глобальным максимумом
(наибольшим значением) и глобальным минимумом (наимень-
шим значением).
Теорема 6 (Вейерштрасса). Если функция f(x) непрерывна
на отрезке, то она достигает на нем своих наименьшего и наи-
большего значений.
Непрерывная на отрезке функция достигает наименьшего
(наибольшего) значений либо на концах отрезка, либо в точках
ее локального экстремума.
Для отыскания глобального экстремума функции f(x) на от-
резке [a, b] необходимо:
1) найти производную
();
yx
′
2) найти критические точки функции;
3) найти значения функции на концах отрезка, т. е. f(a) и
f(b), а также в критических точках, принадлежащих (a, b);
4) из всех полученных значений функции определить наи-
большее и наименьшее ее значения.
График функции
()
yfx
=
называется вогнутым (выпуклым
вниз) на (a, b), если дуга кривой
()
yfx
=
на этом интервале
расположена выше любой касательной, проведенной к графику
этой функции (рис. 17.1).
Рис. 17.1
График функции
()
yfx
=
называется выпуклым (выпуклым
y
x
a
b
0
)(xfy
=
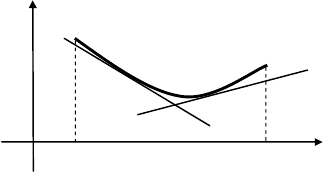
206
вверх) на (a, b), если дуга кривой
()
yfx
=
на этом интервале
расположена ниже любой касательной, проведенной к графику
этой функции (рис. 17.2).
Рис. 17.2
Теорема 7. Если функция f(x) дважды дифференцируема на
(a, b) и
()0
fx
′′
>
(
)
()0
fx
′′
<
всюду на этом интервале, то гра-
фик функции вогнутый (выпуклый) на (a, b).
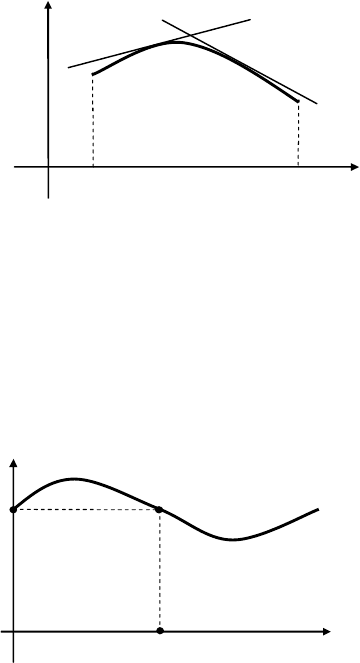
Точка
0
x
такая, что график функции
()
yfx
=
меняет вы-
пуклость на вогнутость или наоборот, проходя через
(
)
00
,()
xfx
,
называется точкой перегиба (рис. 17.3).
Рис. 17.3
Для нахождения точек перегиба вначале находят критиче-
ские точки 2-го рода – те значения x, для которых
()0
fx
′′
=
или
()
fx
′′
не существует. Далее используют достаточные условия
перегиба.
Теорема 8 (первый признак перегиба). Если функция f(x) не-
прерывна в критической точке 2-го рода
0
x
и ее вторая производ-
y
x
a
b
0
()
yfx
=
y
x
(
)
000
,()
Mxfx
()
yfx
=
0
x
207
ная
()
fx
′′
имеет различные знаки слева и справа от
0
,
x
то
0
x
–
точка перегиба.
Теорема 9 (второй признак перегиба). Если функция f(x)
имеет непрерывную производную
()
fx
′′′
в точке
0
,
x
в которой
00
()0,'''()0,
fxfx
′′
=≠
то
0
x
– точка перегиба.
З а м е ч а н и е 2. При исследовании функции и построении ее
графика целесообразно использовать первый признак перегиба, так как
одновременно получаем возможность исследования графика функции
на выпуклость и вогнутость.
План исследования функции и построения графика
1. Найти область определения D(f) функции f(x).
2. Найти область значений E(f) (если это возможно вначале, час-
то E(f) можно указать только по результатам исследования).
3. Исследовать функцию на четность.
4. Исследовать функцию на периодичность.
5. Найти точки пересечения с осью Ox (нули функции) и точки
пересечения с осью Oy.
6. Найти промежутки знакопостоянства функции.
7. Исследовать функцию на непрерывность, дать классифика-
цию разрывов.
8. Найти асимптоты графика функции (горизонтальную, верти-
кальную, наклонную).
9. Исследовать функцию на монотонность и экстремум.
10. Исследовать график функции на выпуклость, вогнутость, пе-
региб.
11. Построить график функции.
Пример 1. Найти экстремумы функции
2
12
.
x
yxe
−
=−⋅
Решение. Подозрительными на экстремумы точками будут те, в
которых производная функции либо равна нулю, либо не существует.
Найдем производную функции:
222
222
121212
1212122
()()()()
(4)(14).
xxx
xxx
yxexexe
exexex
−−−
−−−
′′′′
=−⋅=−⋅+−=
=−−⋅−=−+
Она определена для любого
.
x
∈
R
Приравняем производную к нулю:
2
12
(14)0,
x
ex
−
−+=
значит,
2
140.
x
−+=
Решая это уравнение, по-
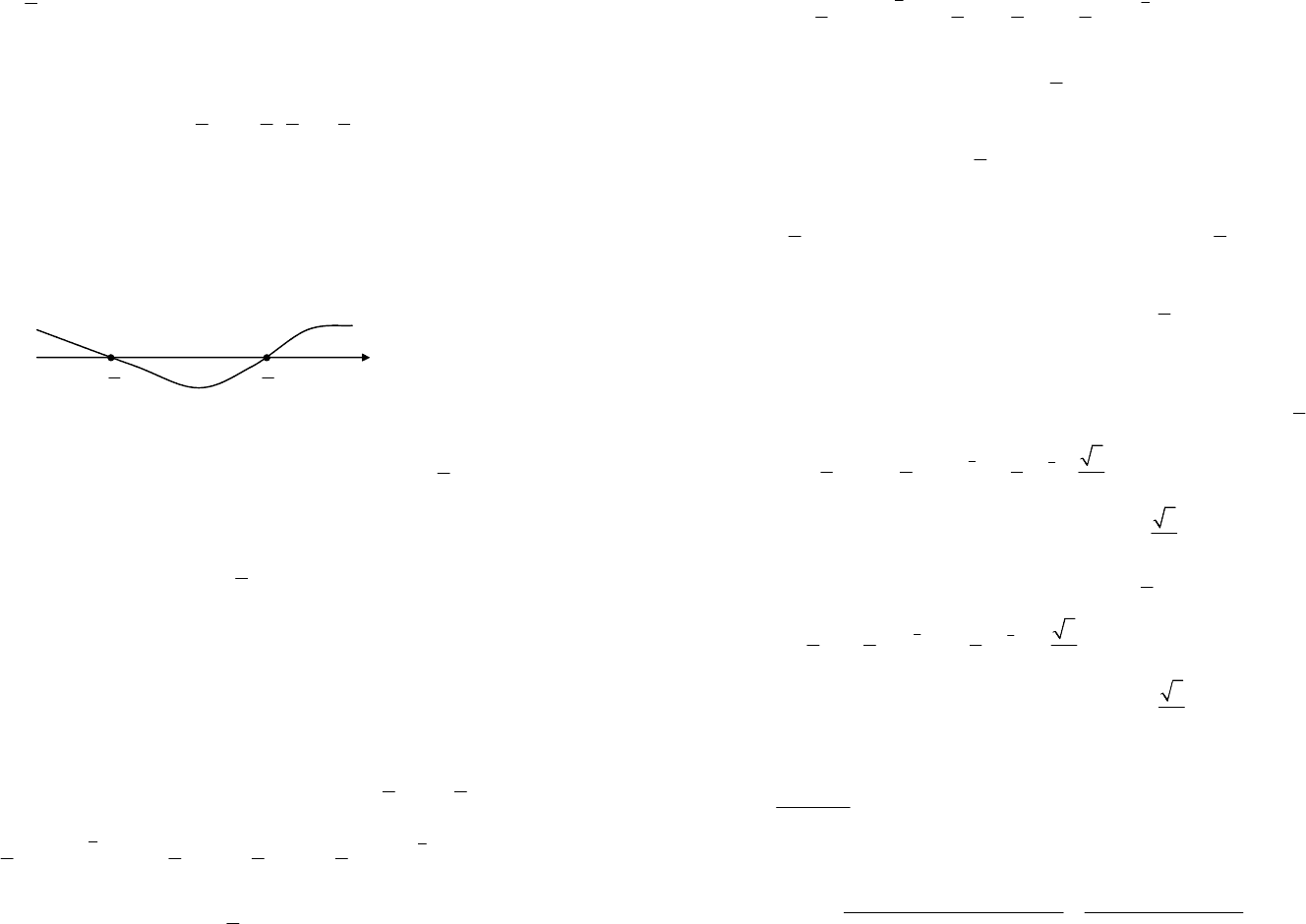
208
лучим
1
.
2
x
=±
Областью определения функции является числовая
прямая.
Исследуем функцию на экстремум в этих точках тремя способами.
1-й способ. Воспользовавшись теоремой 3, исследуем поведение
функции на промежутках
1
,,
2
−∞−
11
,,
22
−
1
,.
2
+∞
Для этого определим знак производной, т. е. выражения
2
122
(14).
x
ex
−
−+ Очевидно, что для всякого
x
∈
R
выполняется нера-
венство
2
12
0.
x
e
−
>
Поэтому знак выражения
()
fx
′
зависит от знака
квадратичного выражения
2
41
x
−
(рис. 17.4).
Рис. 17.4
Так как при «переходе» через точку с абсциссой
1
2
x
=−
произ-
водная
y
′
меняет знак с «+» на «–», то, согласно теореме 1, в этой точ-
ке функция достигает максимума.
При «переходе» через точку
1
2
x
=
производная
y
′
меняет знак с
«–» на «+». Поэтому в данной точке функция достигает минимума.
2-й способ. Воспользуясь теоремой 4, вычислим вторую производ-
ную функции:
(
)
( )
222
2
12212212
123
"(14)'22(14)8
4168.
xxx
x
yexxexex
exxx
−−−
−
=−+=−⋅⋅−++⋅=
=−+
Вычислим ее значение в критических точках
1
2
x
=−
и
1
:
2
x =
2
1
1
3
12
2
2
1111
"416840.
2222
yee
−−
−=⋅−−−+−=−<
Согласно теореме 4, в точке
1
2
x
=
функция достигает максимума.
+
–
+
x
)(xf
′
2
1
−
2
1
209
2
1
1
3
12
2
2
1111
"416840.
2222
yee
−
=⋅−+⋅=>
Согласно теореме 4 в точке
1
2
x
=
функция достигает минимума.
3-й способ. Воспользуемся теоремой 5. Так как производная пер-
вого порядка в точке
1
2
x
=−
равна нулю, а производная второго (чет-
ного) порядка в этой точке меньше нуля, то, согласно теореме 5,
1
2
x
=−
– точка локального максимума. В точке
1
2
x
=
производная
первого порядка также равна нулю, а производная второго (четного)
порядка больше нуля. Следовательно, точка
1
2
x
=
– точка локального
минимума.
Вычислим максимум и минимум функции.
Максимум функции равен значению функции в точке
0
1
:
2
x
=−
( )
2
1
1
2
2
12
1
111
.
2222
e
yee
−−
−
−=−−==
Итак, локальный максимум функции равен
.
2
e
Вычислим значение функции в точке
0
1
:
2
x =
()
2
1
1
2
2
12
1
111
.
2222
e
yee
−
−
=−=−=−
Итак, локальный минимум функции равен
.
2
e
−
Пример 2. Найти наибольшее и наименьшее значения функции
2
1
x
y
xx
=
−−
на отрезке [– 2, 2].
Решение. Найдем точки, которые будут подозрительными на экс-
тремум. Для этого вычислим производную функции
222
2222
(1)(1)1(12)
()
(1)(1)
xxxxxxxxxx
yx
xxxx
′′
−−−−−−−−−
′
===
−−−−

210
222
2222
121
.
(1)(1)
xxxxx
xxxx
−−−+−
==
−−−+
Производная существует во всех точках
.
x
∈
R
Найдем критиче-
ские точки. Полагаем
()0,
yx
′
=
т. е.
2
10.
x
−=
Получаем
1.
x
=±
Обе
точки
1
x
=
и
1
x
=−
принадлежат интервалу (– 2, 2). Поэтому, будем
искать значение функции в этих точках и на концах отрезка. Вычисляем:
22
(2);
2417
f
−
−==
−−−
11
(1);
1113
f
−
−==
−−−
1
(1)1;
111
f
==−
−−
22
(2).
2413
f
==−
−−
Выбрав среди полученных значений наибольшее и наименьшее,
получаем:
.
(1)1,
наим
yy
==−
.
1
(1).
3
наиб
yy
=−=
Пример 3. Дана функция
5
432
311
6.
542
x
yxxxx
=−−+− Вычис-
лить
4,
mM
+
где m и M – соответственно наименьшее и наибольшее
значения функции.
Решение. Найдем производную функции:
5
432432
311
633116.
542
x
yxxxxxxxx
′
′
=−−+−=−−+−
Разложив полученное выражение на множители, получим:
2
(1)(2)(3).
yxxx
′
=−+−
Поскольку функция задана на всей числовой оси (не на отрезке),
то исследуем производную на знак методом интервалов (рис. 17.5).
Рис. 17.5
–
–
+
+
–2
1
3
x
211
В окрестности точки
2
x
=−
выполняется условие
()0, (;2),
()0, (2;1).
fxx
fxx
′
>∀∈−∞−
′
<∀∈−
Поэтому, согласно теореме 3 (первый признак экстремума функ-
ции),
2
x
=−
– точка локального максимума.
В окрестностях точки
1
x
=
производная
y
′
всюду отрицательна.
Поэтому в точке
1
x
=
экстремума нет.
В окрестности точки
3
x
=
выполняется условие
()0, (1;3),
()0, (3;).
fxx
fxx
′
<∀∈
′
>∀∈+∞
Поэтому
3
x
=
– точка локального минимума.
Найдем значения функции в точках минимума и максимума:
273
(3);
20
mf==−
118
(2).
5
Mf=−=
Иных точек локального минимума и максимума функция не имеет.
Искомая величина равна
273118155
4431.
2055
mM
−
+=−⋅+==−
Пример 4. Найти точки перегиба функции
1
ln.
yx
x
=+
Решение. Для данной функции найдем критические точки 2-го ро-
да. Для этого найдем производную 2-го порядка заданной функции:
22
1111
'ln;
x
yx
xx
xx
′
−
=+=−=
()
(
)
()
()
22
'
2
224
2
1''1
12(1)
''
xxxx
xxxx
y
xx
x
−⋅−⋅−
−−−
====
(
)
43
22
2
.
xxx
x
xx
−+
−
==
В точке
2
x
=
полученная производная
()0,
fx
′′
=
а в точке
0
x
=
производная
()
fx
′′
не существует. Поэтому точки
2
x
=
и
0
x
=
явля-
ются критическими точками 2-го рода.
Исследуем функцию на перегиб несколькими способами.
1-й способ. Воспользуемся теоремой 8 (первым признаком переги-
ба). Исследуем вторую производную на знак методом интервалов
(рис. 17.6).

212
Рис. 17.6
В окрестности точки
0
x
=
выполняется условие:
"()0, (;0),
"()0, (0;2).
fxx
fxx
<∀∈−∞
>∀∈
Поэтому, согласно теореме 8,
0
x
=
– точка перегиба функции.
В окрестности точки
2
x
=
выполняется условие:
"()0, (0;2),
()0, (2;).
fxx
fxx
>∀∈
′
<∀∈+∞
Поэтому
2
x
=
– точка перегиба.
2-й способ: Воспользуемся теоремой 9 (второй признак перегиба).
Вычислим:
( )
( )
( )
( )
33
32
3264
3
22
23(2)26
().
xxxx
xxxxx
yx
xxx
x
′
′
−⋅−⋅−
′
−−−−−
′′′
====
Вычислим значение этой производной в точке
2,
x
=
где
()0:
fx
′′
=
4
2261
(2)0.
8
2
y
⋅−
′′′
==−≠
Согласно теореме 9 в точке
2
x
=
функция имеет перегиб.
В точке
0
x
=
заданная функция не определена, однако слева и
справа от нее имеет различный характер выпуклости.
Вычислим значение функции в точке
2:
x
=
1
(2)ln2.
2
y
=+
Получили
1
2;ln2
2
+
– точка перегиба.
Пример 5. Исследовать функцию
( )( )
2
13
yxx
=−+
и построить
ее график.
Решение. Исследование функции произведем согласно указанно-
му выше плану.
1. Область определения функции:
(
)
(
)
;.
Df
=−∞+∞
+
–
–
x
0
2
213
2. Область значений E(f) укажем по результатам исследования.
3. Исследуем функцию на четность и нечетность:
( ) ( ) ( ) ()
2
13.
yxxxyx
−=−−⋅−+≠±
Функция не является четной и нечетной.
4. Функция непериодическая.
5. Найдем точки пересечения графика с координатными осями.
Если у = 0, т. е.
( )( )
2
130,
xx
−+=
то х = 1, х = –3 – точки пересе-
чения с осью Ох (нули функции).
Если х = 0, то у = 3 – точка пересечения с осью Оу.
6. Найдем промежутки знакопостоянства функции с помощью ме-
тода интервалов (рис. 17.7).
Рис. 17.7
Получаем:
(
)
0,
fx
<
если
(
)
;3;
x
∈−∞−
(
)
0,
fx
>
если
(
)
(
)
3;11;.
x
∈−∪+∞
7. Функция непрерывна на всей числовой оси.
8. Горизонтальных асимптот функция не имеет, так как она опре-
делена на всей числовой прямой.
Ищем наклонную асимптоту
.
ykxb
=+
( )( )
2
13
lim.
x
xx
k
x
→±∞
−+
==∞
Функция наклонных асимптот также не имеет.
9. Исследуем функцию на монотонность и экстремум. Найдем
(
)
:
yx
′
( )( )
(
)
( )( ) ( )
( ) ( )
( )
( )( )
22
132131
1231135.
yxxxxx
xxxxx
′
′
=−+=−++−=
=−++−=−+
Производная существует
(
)
;.
x
∀∈−∞+∞
Критическими точками
являются те, для которых
(
)
0,
yx
′
=
т. е.
1
5
3
x
=−
и
2
1.
x
=
Исследуем знак производной для конкретных промежутков, на ко-
торые критические точки делят числовую ось (рис. 17.8).
–
+
+
– 3
1
x
214
Рис. 17.8
Согласно теореме 1, функция возрастает на множестве
( )
5
;1;
3
−∞−∪+∞
и убывает на
5
;1,
3
−
что схематически показа-
но на рис. 17.8. Согласно теореме 3, в точке
5
3
x
=−
она имеет локаль-
ный максимум, а в точке х = 1 – минимум. Найдем их значения:
2
max
555644256
139,5;
3339327
yy
=−=−−⋅−+=⋅=≈
() ( )( )
2
min
111130.
yy
==−+=
10. Исследуем график функции на выпуклость, вогнутость и пере-
гиб. Вычислим производную 2-го порядка:
() ( )( )
( )
( )
135353162.
yxxxxxx
′
′′
=−⋅+=++−=+
Если
(
)
0,
yx
′′
=
то
1
,
3
x
=−
т. е.
1
3
x
=−
– критическая точка 2-го
рода, иных нет.
Имеем
(
)
0,
yx
′′
<
если
1
;
3
x
∈−∞−
и
(
)
0,
yx
′′
>
если
1
;
3
x
∈−+∞
(рис. 17.9).
Рис. 17.9
Значит, график функции является выпуклым на
1
;
3
−∞−
и во-
гнутым на
1
;,
3
−+∞
(согласно теореме 7),
1
3
x
=−
– точка перегиба
+
+
–
1
х
у
3
5
−
у
′
+
–
х
у
1
3
−
у
′
′
215
(теорема 8).
11. Используя полученные данные, построим график функции
(рис. 17.10).
Рис. 17.10
Заметим, что
(
)
(
)
;.
Ef
=−∞+∞
Пример 6. Исследовать функцию
1
2
x
ye
−
= и построить ее график.
Решение. 1. Область определения:
(
)
(
)
(
)
;22;.
Df
=−∞∪+∞
2. Область значений E(f) укажем по результатам исследования.
3. Поскольку область определения D(f) функции не является мно-
жеством, симметричным относительно х = 0, то функция не является
четной и нечетной.
4. Функция непериодическая.
5. График функции не пересекает ось Ох, так как
1
2
0
x
e
−
≠
для
всех
(
)
.
xDf
∈
Если х = 0, то
ye
= – точка пересечения с осью Оу.
6. Для всех
(
)
xDf
∈ выполняется
1
2
0,
x
e
−
>
т. е. функция поло-
жительна на всей области определения.
7. Функция непрерывна на своей области определения, х = 2 – точ-
ка разрыва.
–3
1
3
−
5
3
−
1
х
у
3
9
10
