Майсеня Л.И. Математика в примерах и задачах. Часть 3
Подождите немного. Документ загружается.

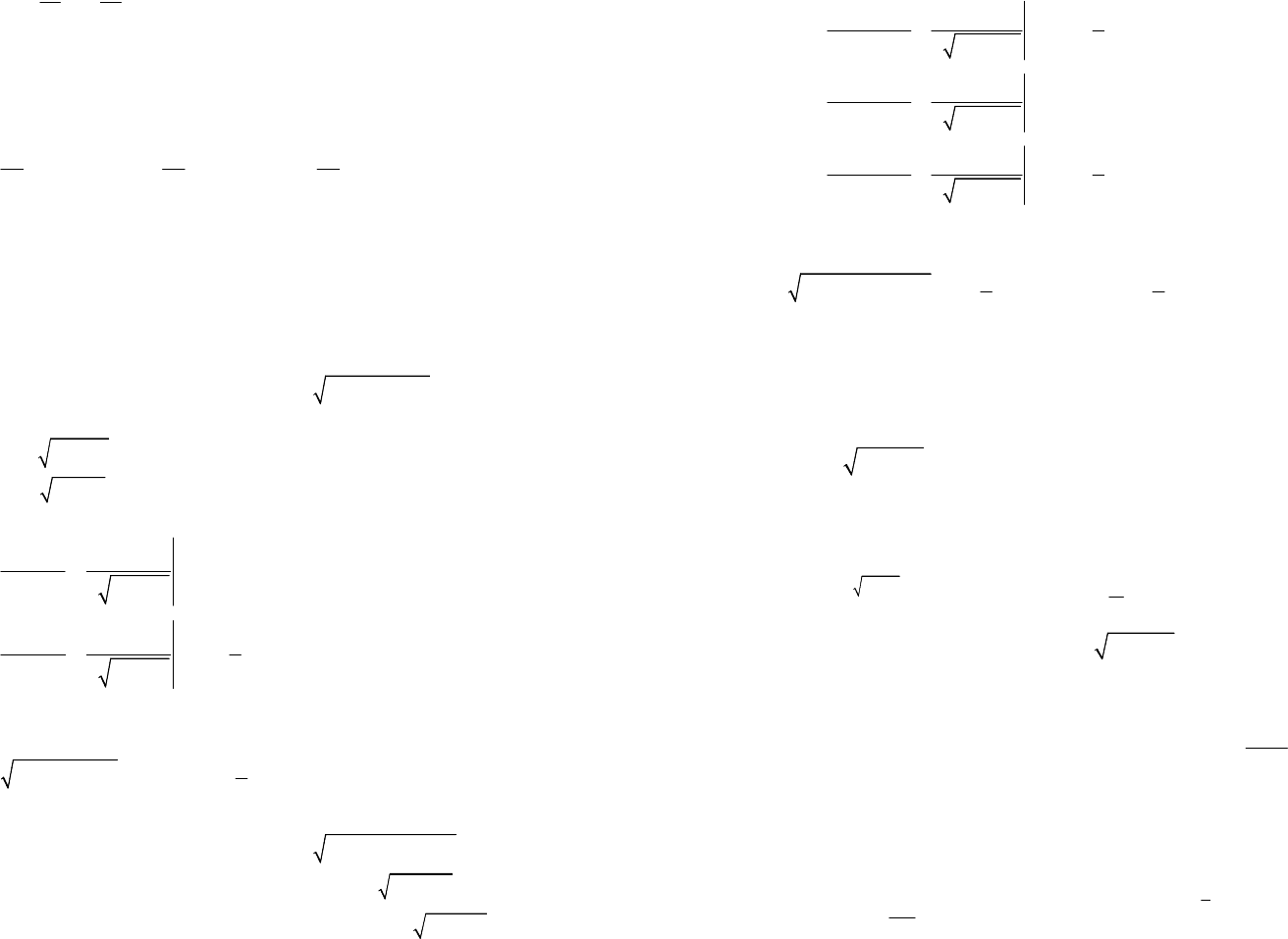
236
( )
.
xy
zz
dzdxdyeydxxdy
xy
∂∂
=+=+
∂∂
Пример 4. Найти
(
)
1,1,
due
− функции
2
.
xy
uz=
Решение. Используя формулу (18.6), вычислим частные произ-
водные:
2
ln2;
xy
u
zzxy
x
∂
=⋅
∂
2
2
ln;
xy
u
zzx
y
∂
=⋅
∂
2
21
.
xy
u
xyz
z
−
∂
=
∂
Тогда
222
221
2lnln.
xyxyxy
duxyzzdxxzzdyxyzdz
−
=++
Подставим
1,
x
=−
1,
y
=
.
ze
=
Получим:
(
)
1,1,2.
dueedxedydz
−=−++
Пример 5. Вычислить приближенно
33
0,091,01.
+
Решение. Используем формулу (18.7). Рассмотрим функцию
33
(;)
fxyxy
=+ и найдем ее значение при
0, 1:
xy
==
33
(0; 1)011.
f
=+=
Вычислим значения частных производных функции f в точке (0; 1).
2
33
(0; 1)
(0, 1)3
0;
2
fx
x
xy
∂
==
∂
+
2
33
(0; 1)
(0, 1)33
.
2
2
fy
y
xy
∂
==
∂
+
Приращения аргументов
0,09; 0,01.
xy
∆=∆=
Тогда по формуле (18.7) имеем:
33
3
0,091,01100,090,011,015.
2
+≈+⋅+⋅=
Пример 6. Вычислить приближенно
2,990,005
1,023.
e+
Решение. Рассмотрим функцию
(;;)3
yz
fxyzxe
=+ и найдем ее
значение при
1, 3è 0.
xyz
===
Имеем:
30
(1; 3; 0)132.
fe
=+=
237
Вычислим значения частных производных в точке (1; 3; 0):
1
(1; 3; 0)
(1; 3; 0)
(1; 3; 0)
(1, 3, 0)3
;
4
23
(1, 3, 0)ln
0;
23
(1, 3, 0)33
.
4
23
y
yz
y
yz
z
yz
fyx
x
xe
fxx
y
xe
fe
z
xe
−
∂
==
∂
+
∂
==
∂
+
∂
==
∂
+
Приращение аргументов
0,02; 0,01; 0,005.
xyz
∆=∆=−∆=
Используя далее формулу (18.8), получаем:
2,990,005
33
1,02320,020(0,01)0,0052,018752,019.
44
e+≈+⋅+⋅−+⋅=≈
Задания
I уровень
1.1. Найдите частные производные первого порядка функции:
1)
3
32;
zxy
=+ 2)
322
64231;
zxxyxyxy
=−+−++
3)
24
sin;
z
ρυ
= 4)
(
)
(
)
(
)
.
uxyzxyz
=−−−
1.2. Найдите полный дифференциал функции:
1)
33
;
xy
ze
−
= 2)
ln1;
y
z
x
=+
3)
(
)
sin;
zxy
= 4)
322
.
uyxz
=++
1.3. Вычислите приближенно значение:
1)
3,02
1,09;
2)
(
)
22
ln0,950,03;
+ 3)
0,97
arctg.
1,04
II уровень
2.1. Найдите частные производные и вычислите их значения
в указанной точке М
0
:
1)
2
arctg,
y
z
x
=
(
)
0
1;1;
M 2)
,
x
y
ze
=
(
)
0
0;1;
M
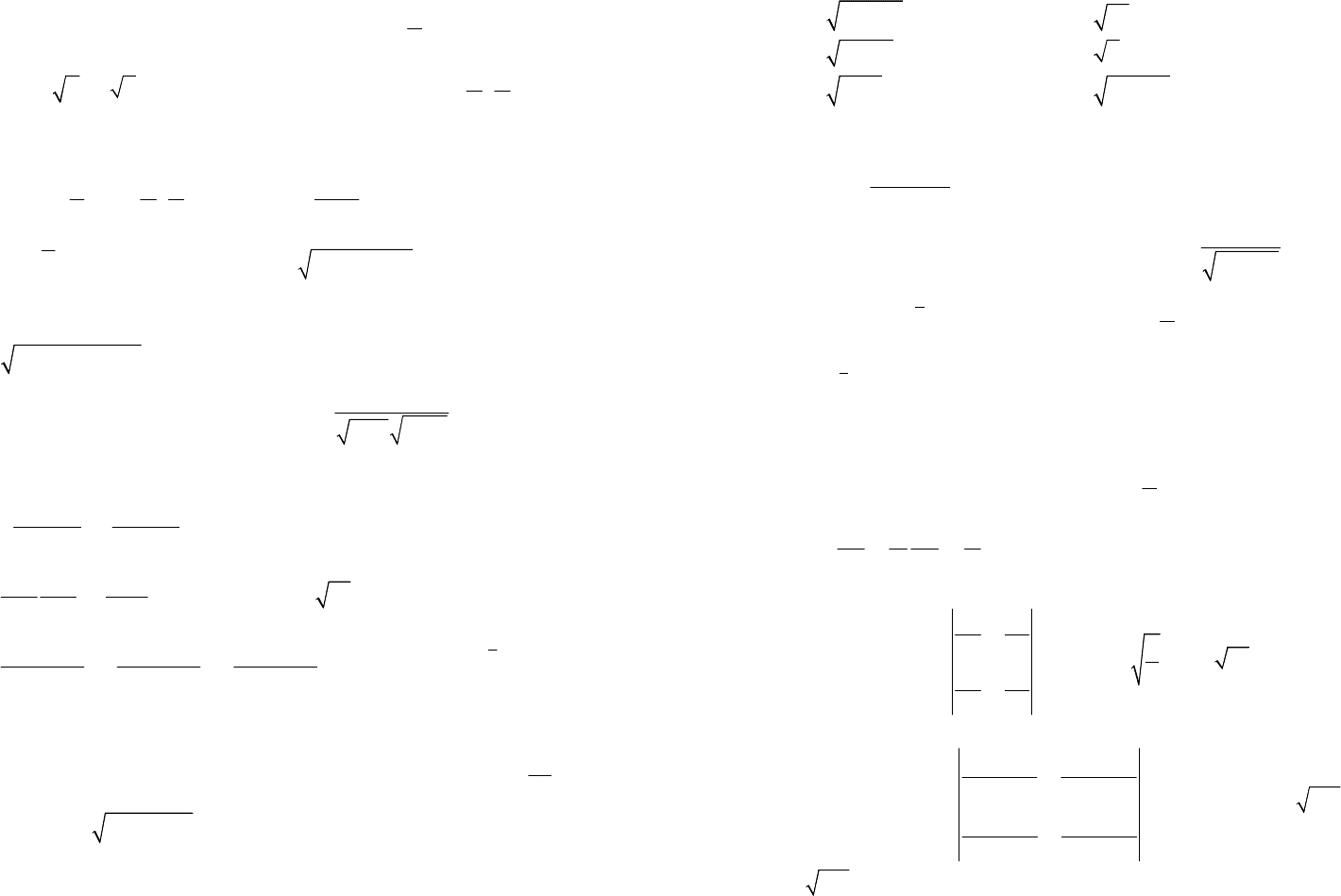
238
3)
( )
3
1,
y
zx=−
(
)
0
1;1;
M − 4)
ln,
x
zx
y
=
(
)
0
;;
Mee
5)
4
3,
uxyzx
=+
(
)
0
1;1;0;
M 6)
sin
,
xy
ze=
0
;.
22
M
ππ
2.2. Найдите дифференциал функции в точке М
0
:
1)
lntg,
x
z
y
=
0
;;
44
M
ππ
2)
arctg,
x
z
xy
=
−
(
)
0
2;1;
M
3)
,
xz
y
ue
=
(
)
0
1;1;1;
M 4)
(
)
222
ln,
uxyz
=++
(
)
0
1;0;1.
M
−
2.3. Вычислите приближенно:
1)
3,993
4
1,030,07;
+ 2)
( )
1,98
ln2,74;
3)
23
1,0022,0033,004;
⋅⋅ 4)
2
3
4
3
1,03
.
0,981,05
2.4. Вычислите:
1)
(,)(,)
23,
fxyfxy
xy
∂∂
−
∂∂
если
(;)arctg(2);
fxyxy
=−
2)
2
222
22
,
fff
xy
xy
∂∂∂
−
∂∂
∂∂
если
(
)
,;
fxyxy
=
3)
(,,)(,,)(,,)
,
uxyzuxyzuxyz
xyz
xyz
∂∂∂
++
∂∂∂
если
(;;).
x
y
uxyzz
=
III уровень
3.1. Определите, существует ли частная производная
z
y
∂
∂
функции
22
1
zxy
=−− в точке (1; 0).
3.2. Установите, имеет ли заданная функция частные произ-
водные в точке
(
)
0;0
O и дифференцируема ли она в этой точке:
239
1)
22
;
zxy
=+ 2)
3
;
zxy
=
3)
3
sin;
zyx
= 4)
5
tg;
zxy
=
5)
22
3
;
zxy
= 6)
44
4
.
zxy
=+
3.3. Найдите частные производные функции:
1)
sin
arctg;
1sin
xy
z
yx
+
=
−
2)
(
)
cossin;
xyz
uezxyx
=+
3)
( )( )( )
23
111;
uxyz
=+++ 4)
22
arcsin;
x
z
xy
=
+
5)
( )
tg;
y
x
zxye
=− 6)
;
x
z
u
y
=
7)
;
z
x
uy
= 8)
;
x
y
uz
=
9)
;
zxy
uxyz
= 10)
arctgarctgarctg.
uxyz
=++
3.4. Покажите, что функция
sin
x
zx
y
= удовлетворяет урав-
нению
.
zyzz
xxyx
∂∂
+=
∂∂
3.5. Вычислите
,
xx
uv
yy
uv
∂∂
∂∂
∂∂
∂∂
если
, .
u
xyuv
v
==
3.6. Найдите
(
)
(
)
( ) ( )
00
00
,
xMxM
uv
yMyM
uv
∂∂
∂∂
∂∂
∂∂
если
3
2
,
xuv
=
3
2
,
yuv
=
(
)
0
1;2.
M
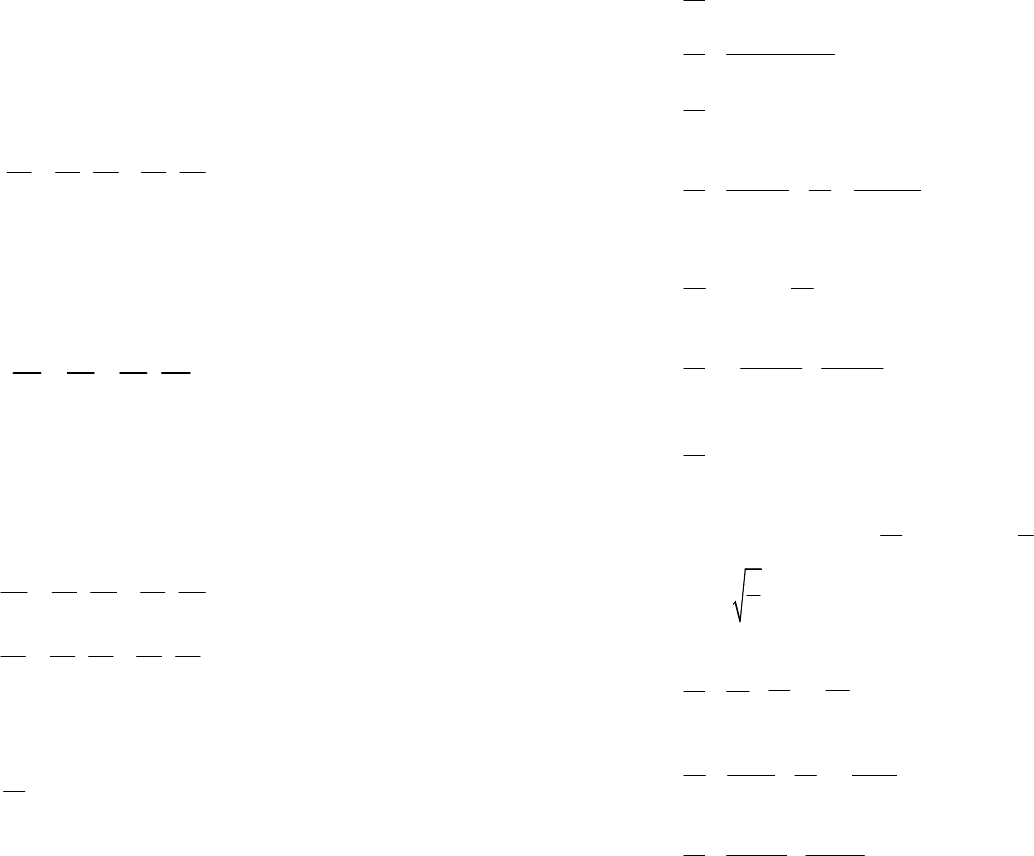
240
18.3. Дифференцирование сложных функций
Пусть
(
)
;,
zfxy
= где
(
)
(
)
, ,
xxtyyt
== причем
(
)
;
fxy
имеет непрерывные частные производные, функции
(
)
,
xt
(
)
yt
имеют непрерывные производные, t – независимая переменная.
Тогда производная сложной функции
(
)
(
)
(
)
;
zfxtyt
= вычис-
ляется по формуле
.
dzzdxzdy
dtxdtydt
∂∂
=⋅+⋅
∂∂
(18.9)
Пусть
(
)
;
zfxy
= и
(
)
,
yyx
= где x – независимая перемен-
ная, причем функция
(
)
;
fxy
имеет непрерывные частные про-
изводные,
(
)
yx
– непрерывную производную. Тогда справедли-
ва формула полной производной функции z по x:
.
dzzzdy
dxxydx
∂∂
=+⋅
∂∂
(18.10)
Пусть
(;)
zfxy
=
и
(;),
xxuv
=
(;),
yyuv
=
причем функция
(
)
;
fxy
имеет непрерывные частые производные по x и y, а
функции
(
)
;,
xuv
(
)
;
yuv
имеют непрерывные частные произ-
водные по u и v. Тогда частные производные функции z по u и v
находят по формулам:
,
.
zzxzy
uxuyu
zzxzy
vxvyv
∂∂∂∂∂
=⋅+⋅
∂∂∂∂∂
∂∂∂∂∂
=⋅+⋅
∂∂∂∂∂
(18.11)
Формулы (18.9)–(18.11) обобщаются на любое конечное ко-
личество переменных (зависимых и независимых).
Пример 1. Найти
dz
dt
двумя способами (свести к функции одной
переменной t и по формуле (18.9)), если
(
)
22
ln,
zxy
=+ где
cos,
xt
=
sin.
yt
=
Решение. 1-й способ. Подставив вместо x, y заданные выражения,
241
получим:
(
)
22
lncossin
ztt
=+ – функцию одной переменной t. Тогда
( )
( )
( )
22
22
lncossin;
1
2cossin2sincos;
cossin
2cossin2sincos0.
t
dz
tt
dt
dz
tttt
dt
tt
dz
tttt
dt
′
=+
=−+
+
=−+=
2-й способ. Найдем частные производные по x и y функции z:
22
2
;
zx
x
xy
∂
=
∂
+
22
2
.
zy
y
xy
∂
=
∂
+
Вычисляем производные функций
(
)
xt
и
(
)
:
yt
sin;
dx
t
dt
=−
cos.
dy
t
dt
=
По формуле (18.9) получаем:
2222
2sin2cos
.
dzxtyt
dt
xyxy
=−+
++
Заменив x и y их выражениями через t, получим:
2cossin2sincos0.
dz
tttt
dt
=−+=
Пример 2. Вычислить
dz
dt
в точке
0
,
4
t
π
= если
ln,
x
z
y
= где
2
tg,
xt
=
2
ctg.
yt
=
Решение. Находим частные производные заданной функции
(
)
,:
zxy
1
;
2
z
xx
∂
=
∂
1
.
2
z
yy
∂
=−
∂
Вычисляем
2
2tg
;
cos
dxt
dt
t
=
2
2ctg
.
sin
dyt
dt
t
=−
По формуле (18.9) получаем:
22
tgctg
.
cossin
dztt
dt
xtyt
=+
Делаем замену переменных:
242
22
111144
.
sincossincos2sincossin2
tgcosctgsin
dz
dtttttttt
tttt
=+=+==
Вычислим значение
dz
dt
в точке
0
:
4
t
π
=
4
4.
4
sin2
4
z
π
π
′
==
⋅
Пример 3. Вычислить различными способами
x
z
′
функции
( )
sin,
y
zx
= где
tg.
yx
=
Решение. 1-й способ. Используем метод логарифмического диф-
ференцирования. Прологарифмируем равенство, задающее функцию:
( )
lnlnsin
y
zx
= или
(
)
lnlnsin.
zyx
=
Дифференцируем по
x
полученное равенство, считая
(
)
:
zzx
=
() ()
( )
lnlnsin;
xx
zyx
′
′
=
()
lnsinlnsin;
x
x
x
z
yxyx
z
′
′
′
=+
(
)
2
lnsin
cos
.
sin
cos
x
x
yx
zz
x
x
′
=+
Подставляя вместо z и y заданные выражения из условия, получаем:
( )
(
)
tg
2
lnsin
sin1.
cos
x
x
x
zx
x
′
=+
2-й способ. Найдем частные производные:
( )
1
sincos;
y
z
yxx
x
−
∂
=
∂
()()
sinlnsin.
y
z
xx
y
∂
=
∂
Вычисляем производную функции у:
2
1
.
cos
dy
dx
x
=
Теперь по формуле (18.10) получаем:
( )
( ) ( )
( )
( )
1
22
sinlnsinlnsin
cos
sincossin
sin
coscos
y
yy
x
xxx
x
zyxxxy
x
xx
−
′
=+=+
или
( )
(
)
tg
2
lnsin
sin1.
cos
x
x
x
zx
x
′
=+
Пример 4. Найти
,
u
z
′
v
z
′
функции
23
2,
zxy
=+ если
,
uv
xe
=
22
.
yuv
=−
243
Решение. Используя формулу (18.11), найдем частные произ-
водные:
4,
z
x
x
∂
=
∂
,
uv
x
ev
u
∂
=
∂
;
uv
x
eu
v
∂
=
∂
2
3,
z
y
y
∂
=
∂
2,
y
u
u
∂
=
∂
2.
y
v
v
∂
=−
∂
По формуле (18.11) получим:
2
2
46,
46
uv
u
uv
v
zxve ó u
zxueyv
′
=+
′
=−
или
( )
( )
2
222
2
222
46,
46.
uv
u
uv
v
zveuuv
zuevuv
′
=+−
′
=−−
Заметим, что этот пример можно решать и вторым способом –
вначале подставить вместо x, y их выражения через u, v, а затем – найти
частные производные по u, v.
Пример 5. Найти
x
u
′
функции
,
uxyz
= где
sin,
yx
=
cos
zx
=
при
0
.
4
x
π
=
Решение. 1-й способ. Подставив в исходную функцию
sin,
yx
=
cos,
zx
=
получим функцию одной переменной:
cossin.
uxxx
=
Дифференцируем по x:
( ) ( ) ( )
cossin2cossinsin2
sin22cos2
.
2cossin4cossin22sin222sin2
x
xxxxxxxx
xxx
u
xxxxxxxxxx
′′′
+
′
====
2-й способ. Найдем частные производные:
,
2
yz
u
x
x
∂
=
∂
,
2
uxz
y
y
∂
=
∂
,
2
xy
u
z
z
∂
=
∂
а также производные:
cos,
dy
x
dx
=
sin.
dz
x
dx
=−
По формуле (18.10) получаем:
cossin.
222
yzxy
duxz
xx
dx
xyz
=+−
После замены переменных получим:
22
sincoscossinsin22cos2
.
2sincos22sin2
x
duxxxxxxxxx
u
dx
xxxxx
+−+
′
===

244
Пришли к такому же аналитическому выражению для
,
x
u
′
что и в
первом способе решения.
Вычислим
x
u
′
в точке
0
:
4
x
π
=
sin22cos2
1
444
.
4
2
22sin2
44
x
u
πππ
π
πππ
⋅+⋅⋅
′
==
⋅
Задания
I уровень
1.1. Найдите
dz
dx
функции, при
0
:
xx
=
1)
,
xy
z
xy
=
+
где
0
1
3, ;
2
yxx
=−=
2)
3
,
zxy
= где
0
sin, .
2
yxx
π
==
1.2. Найдите
dz
dt
функции
1
ln,
3
x
z
y
= где
cos3,
xt
=
sin3.
yt
=
1.3. Найдите частные производные
u
z
′
и
:
v
z
′
1)
,
xy
ze
= где
, ;
xuvyuv
=+=−
2)
33
,
zxy
=+ где
, ;
u
xuvy
v
==
3)
,
y
zx
= где
sin, cos.
xuyv
==
1.4. Найдите производную
y
u
′
функции:
1)
23
,
uxyz
= где
,
xy
=
;
y
ze
=
2)
(
)
,
yxz
ue
+
= где
2
ln, ln.
xyzy
==
245
II уровень
2.1. Найдите двумя способами
z
t
∂
∂
и
z
τ
∂
∂
функции:
1)
2
,
y
x
ze
= где
cos,
xt
τ
=
sin;
yt
τ
=
2)
tg,
zxy
=
где
tg,
x
τ
=
ctg;
yt
=
3)
ctg,
x
zar
y
=
где
sin,
xt
τ
=
cos.
yt
τ
=
2.2. Найдите
du
dx
функции u в точке
0
:
x
1)
2
cossin,
uzyx
= где
,
yx
=
ctg,
zx
=
0
;
4
x
π
=
2)
(
)
23
ln1,
uyxz
=++ где
2
,
yx
=
1
ln,
z
x
=
0
1;
x
=
3)
(
)
coscos,
uxyyz
=− где
1
,
sin
y
x
=
1
,
cos
z
x
=
0
3
.
4
x
π
=
2.3. Найдите частные производные
,
x
u
′
y
u
′
и
z
u
′
функции:
1)
,
ue
ξη
τ
+
= где
,
x
τ
=
,
xy
ξ
=
;
xyz
η
=
2)
(
)
ln,
u
τξξη
= где
,
xy
τ =
,
yz
ξ =
.
xz
η =
2.4. Покажите, что функция
22
yx
zxe
−
=
удовлетворяет урав-
нению
2
11
.
zzz
xxyy
x
∂∂
+=
∂∂
III уровень
3.1. Найдите частные производные
,
x
u
′
y
u
′
и
z
u
′
функции в
точке
0000
(,,):
Nxyz
1)
,
u
τξη
=
где
22
,
xy
τ =−
22
,
yz
ξ =−
22
,
zx
η =− N
0
(1; 1; 1);
246
2)
sinsin
,
coscos
u
τξ
τη
−
=
+
где
22
,
xy
τ =+
22
,
yz
ξ =+
22
,
xz
η =+
0
(;;).
N
πππ
3.2. Вычислите определитель:
1)
,
xx
r
yy
r
ϕ
ϕ
∂∂
∂∂
∂∂
∂∂
если
2
4cos,
xr
ϕ
=
2
2sin;
yr
ϕ
=
2)
,
xxx
r
yyy
r
zzz
r
ϕθ
ϕθ
ϕθ
∂∂∂
∂∂∂
∂∂∂
∂∂∂
∂∂∂
∂∂∂
если
cossin,2sinsin,3cos;
xryrzr
ϕθϕθθ
===
3)
,
xxx
yyy
zzz
ξηζ
ξηζ
ξηζ
∂∂∂
∂∂∂
∂∂∂
∂∂∂
∂∂∂
∂∂∂
если
,
x
ξηζ
=
,
y
ξηξηζ
=−
.
z
ηξη
=−
3.3. Проверьте равенства:
1)
( )
22
,
zz
xyxyxyz
xy
∂∂
−+=
∂∂
если
2
2
2
;
x
y
y
zeye=
2)
3
,
uuu
xyzxyz
∂∂∂
++=
∂∂∂++
если
(
)
333
ln3;
uxyzxyz
=++−
3)
0,
uuu
xyz
xyz
∂∂∂
++=
∂∂∂
если
.
z
y
x
u
y
=
247
18.4. Дифференцирование неявных функций
Допустим, что функция
(
)
yyx
= задана неявно уравнением
(
)
;0
Fxy
=
(18.12)
и требуется найти
(
)
.
yx
′
1-й способ. Если практически возможно, из (18.12) выража-
ют явно
y
через
x
и дифференцируют.
2-й способ. Дифференцируют уравнение (18.12), считая
(
)
,
yyx
= и выражают затем
(
)
.
yx
′
3-й способ. Используют формулу
()
(
)
( )
;
,
;
x
y
Fxy
yx
Fxy
′
′
=−
′
(18.13)
если
(
)
;0.
y
Fxy
′
≠
Способы 1–2 были рассмотрены в теории дифференцирова-
ния функции одной переменной и не всегда являются рацио-
нальными.
Производные неявной функции
(
)
yfx
= порядка выше
первого находят последовательным дифференцированием фор-
мулы (18.13), учитывая, что y – функция от x.
Для нахождения частных производных функции
(
)
;,
zzxy
=
заданной неявно уравнением
(
)
;;0,
Fxyz
=
(18.14)
используют формулы
, ,
y
x
xy
zz
F
F
zz
FF
′
′
′′
=−=−
′′
(18.15)
при условии, что эти производные существуют и
0.
z
F
′
≠
Пример 1. Для функции
(
)
,
yyx
= заданной неявно уравнением
33
10,
xy
++=
найти
y
′
всеми возможными способами.
Решение. Используем 1-й способ. Выражаем y через x и диффе-
ренцируем по x:
3
3
1;
yx
=−−
() ( )
2
2
3232
33
1
3.
3(1)(1)
x
yxx
xx
′
=−=−
−−−−

248
Таким образом,
2
2
.
x
y
y
′
=−
Используем 2-й способ. Продифференцируем по x заданное урав-
нение, считая
():
yyx
=
22
330.
x
xyy
′
+=
Отсюда выражаем
:
x
y
′
2
2
3
3
x
x
y
y
′
=−
или
2
2
.
x
x
y
y
′
=−
Используем 3-й способ. Применим формулу (18.13):
33
(;)1;
Fxyxy
=++
2
3,
x
Fx
′
=
2
3.
y
Fy
′
=
По формуле (18.13) получаем:
2
2
3
3
x
x
y
y
′
=−
или
2
2
.
x
x
y
y
′
=−
Вывод: способы 2 и 3 оказались наиболее рациональными.
Пример 2. Найти
y
′
функции
(
)
,
yyx
= заданной неявно уравне-
нием
ln.
yxy
=+
Решение. Используем 3-й способ.
(;)ln;
Fxyxyy
=+−
1,
x
F
′
=
1
1.
y
F
y
′
=−
По формуле (18.13) получаем:
1
.
1
11
1
x
yy
y
yy
y
′
=−=−=
−−
−
Таким образом,
.
1
x
y
y
y
′
=
−
Пример 3. Найти
y
′
в точке
0
x
=
функции
(
)
,
yyx
= заданной
неявно уравнением
23
sin1.
xyyx
++=
Решение. Вычислим
y
′
по формуле (18.13):
(
)
23
;sin1,
Fxyxyyx
=++−
2cos,
x
Fxyx
′
=+
2
3sin;
y
Fyx
′
=+
249
2
2cos
.
3sin
x
y
F
xyx
y
F
yx
′
+
′
=−=−
′
+
Пусть
0
0.
x
=
Вычислим
(
)
0
,
yx
подставив
0
x
=
в исходное урав-
нение:
3
sin01,
yy
+=
1.
y
=
Тогда
()
1cos01
0.
3sin03
y
⋅
′
=−=−
+
Пример 4. Найти
x
z
′
0
(),
M
y
z
′
0
()
M
функции
(
)
;,
zzxy
= задан-
ной неявно уравнением
2
1,
xxyz
=+
если
0
(1,1).
M
Решение. Воспользуемся формулой (18.15) для функции
(
)
2
;;1.
Fxyzxxyz
=−−
Вычисляем:
2,
F
xyz
x
∂
=−
∂
,
F
xz
y
∂
=−
∂
.
F
xy
z
∂
=−
∂
Тогда по формуле (18.15) имеем:
22
;
x
xyzxyz
z
xyxy
−−
′
=−=
−
.
y
xzz
z
xyy
−
′
=−=−
−
Для заданной точки
(
)
0
1,1
M найдем соответствующее значение
(
)
00
.
zzM= Для этого подставим
1,
x
=
1
y
=
в уравнение, которое
задает неявно функцию z:
11.
z
=+
Получаем
0
0.
z
=
Подставив значе-
ния
1,
x
=
1,
y
=
0
z
=
в выражения
x
z
′
и
,
y
z
′
получим
(
)
0
2;
x
zM
′
=
(
)
0
0.
y
zM
′
=
Задания
I уровень
1.1. Найдите
y
′
функции:
1)
2
10;
y
exx
−−+=
2)
(
)
ln1cos0;
xy
−−=
3)
arctg0;
yxy
+=
4)
( )
cossin;
x
xy
y
+=
250
5)
(
)
ln0;
xyx
+=
6)
23
320;
x
xy
y
++=
7)
32;
yx
xye
−
−= 8)
(
)
(
)
2
2222
34.
xyxxy
+−=+
1.2. Найдите
,
z
x
∂
∂
z
y
∂
∂
функции z, заданной неявно уравне-
нием:
1)
41
;
z
xyze
+
−−= 2)
sin3;
xy
z
−
=
3)
23
16;
yxyzz−+= 4)
222
4.
xyz
++=
II уровень
2.1. Найдите
dz
функции, если:
1)
lnlnln1;
xyyxzx
++=
2)
;
z
y
xze
=
3)
coscoscos1;
yxxzzy
++=
4)
arctg0.
x
yz
zy
+−=
−
2.2. Дано уравнение
(
)
.
yx
xyyx
=≠ Найдите
(
)
yx
′
двумя
способами.
2.3. Дано уравнение
(
)
22
ln
arctg0.
2
xy
x
y
+
−=
Найдите
,
x
′
если
(
)
.
xxy
=
2.4. Найдите частные производные
( )
0
z
M
x
∂
∂
и
( )
0
z
M
y
∂
∂
функции:
1)
32
16,
zxyzy−+=
(
)
0
1; 4;
M
2)
(
)
22
35,
xyzxzxy
+=+
(
)
0
1; 2;
M −
3)
333
9,
xzxzy
+−=
(
)
0
3;3.
M
251
2.5. Найдите частные производные функции:
1)
2222
tg;
zz
xyxy
=
−−
2)
(
)
1;
xyz
exyz
++
++=
3)
ln;
z
zxz
y
=− 4)
1.
xyxzyz
++=
III уровень
3.1. Найдите производные функций
(
)
,
xxt
=
(
)
yyt
= в точ-
ке
0
2,
t
=
если функции заданы системой уравнений
(
)
222
2,
2
xyt
xyt
+=
++=
и удовлетворяют условиям
(
)
21,
x
=
(
)
21.
y
=−
3.2. Найдите производные
(
)
0,
x
′
(
)
0
z
′
неявных функций
(
)
,
xxt
=
(
)
,
zzt
= удовлетворяющих условиям
(
)
01,
x
=−
(
)
01
z
=
и заданных системой уравнений:
1)
222
,
2;
xzt
xzt
+=−
+=−
2)
222
22
2,
20.
xtz
xxttz
+=+
+++−=
3.3. Докажите, что неявная функция
(
)
;,
zfxy
= определяе-
мая уравнением
222
,
y
z
xyzye
++= удовлетворяет уравнению
( )
222
22.
zz
xyzxyxz
xy
∂∂
−−+=
∂∂
3.4. Докажите, что неявная функция
(
)
;,
xfyz
= определяе-
мая уравнением
240,
zxyx
−+−=
является решением урав-
нения
241.
xx
zy
∂∂
+=
∂∂
3.5. Докажите, что неявная функция
(
)
;,
zfuv
= заданная
252
уравнением
2,
zz
uv
vv
e
++
=
удовлетворяет уравнению
.
zz
uvzuv
uv
∂∂
+=−
∂∂
3.6. Найдите дифференциал функции
(
)
;;,
zfxyz
= задан-
ной уравнением
3
0
zxzy
−+=
в точке
(
)
3;2
−
и удовлетворяю-
щей условию
(
)
3;22.
f
−=
3.7. Найдите дифференциалы функций
(
)
;
xxuv
= и
(
)
;,
yyuv
= заданных системой уравнений
,
sin
.
sin
xyuv
xu
yv
+=+
=
18.5. Касательная плоскость и нормаль к поверхности
Пусть поверхность задана уравнением
(
)
;,
zfxy
=
(
)
2
;.
xyDR
∈⊆
Тогда уравнение касательной плоскости в точке
(
)
000
;
Mxy
имеет вид:
(
)
( )
(
)
( ) ( )
00
000
0,
fMfM
xxyyzz
xy
∂∂
−+−−−=
∂∂
(18.16)
где
(
)
000
;.
zfxy
=
Нормалью к поверхности в точке
(
)
0000
;;,
Nxyz
(
)
000
;,
zfxy
= называется прямая, проходящая через точку
0
N
перпендикулярно к касательной плоскости в этой точке.
Уравнение нормали к поверхности (18.16) в точке
(
)
000
;
Mxy
имеет вид:
( ) ( )
000
00
.
1
xy
xxyyzz
fMfM
−−−
==
′′
−
(18.17)
Если поверхность задана уравнением
253
(
)
;;0
Fxyz
=
(18.18)
и в точке
(
)
0000
;;
Nxyz
этой поверхности существуют частные
производные
(
)
0
,
FN
x
∂
∂
(
)
0
,
FN
y
∂
∂
(
)
0
,
FN
z
∂
∂
не равные нулю од-
новременно, то уравнение касательной плоскости к поверхности
(18.18) в точке
(
)
0000
;;
Nxyz
имеет вид:
(
)
( )
(
)
( )
(
)
( )
000
000
0.
FNFNFN
xxyyzz
xyz
∂∂∂
−+−+−=
∂∂∂
(18.19)
Уравнение нормали к поверхности (18.18) в точке
(
)
0000
;;
Nxyz
имеет вид:
( ) ( ) ( )
000
000
.
xyz
xxyyzz
FNFNFN
−−−
==
′′′
(18.20)
Пример 1. Поверхность задана уравнением
22
.
zyxxy
=+ Соста-
вить уравнение касательной плоскости и уравнение нормали к поверх-
ности в точке
(
)
0
1; 1.
M
Решение. Найдем частные производные:
2
2;
z
xyy
x
∂
=+
∂
2
2.
z
xxy
y
∂
=+
∂
Их значения в точке
(
)
0
1;1
M равны
(
)
0
3,
zM
x
∂
=
∂
(
)
0
3.
zM
y
∂
=
∂
Найдем соответствующее значение
0
z
функции для
(
)
0
1;1:
M
0
2.
z
=
Тогда уравнение касательной плоскости примет вид:
(
)
(
)
(
)
313120,
xyz
−+−−−=
или
3340.
xyz
+−−=
Уравнение нормали:
112
.
331
xyz
−−−
==
−
Пример 2. Составить уравнение касательной плоскости и нормали
к поверхности
33
330
z
xye
+−+=
в точке
(
)
0
1;1;0.
N −

254
Решение. Частные производные имеют вид:
2
3;
F
x
x
∂
=
∂
2
3;
F
y
y
∂
=
∂
3.
z
F
e
z
∂
=−
∂
Их значения в точке N
0
равны:
(
)
0
3,
FN
x
∂
=
∂
(
)
0
3,
FN
y
∂
=
∂
(
)
0
3.
FN
z
∂
=−
∂
Тогда уравнение касательной плоскости в точке N
0
:
(
)
(
)
313130
xyz
−++−=
или
0.
xyz
+−=
Уравнение нормали:
11
.
333
xyz
−+
==
−
Пример 3. Составить уравнения касательных плоскостей к по-
верхности
222
329,
xyz
−+=
параллельных плоскости
2.
xyz
+−=
Решение. Найдем частные производные:
6,
F
x
x
∂
=
∂
4,
F
y
y
∂
=−
∂
2.
F
z
z
∂
=
∂
Так как касательная плоскость параллельна плоскости
2,
xyz
+−=
то справедливо условие параллельности плоскостей:
(
)
(
)
(
)
0
00
,
111
y
xz
FN
FNFN
′
′′
==
−
т. е.
642.
xyz
=−=−
Координаты точек касания найдем из системы уравнений
222
642,
329.
xyz
xyz
=−=−
−+=
Решая систему, получаем:
30
,
5
x =±
330
,
10
y = m
330
.
5
z = m
Точки касания имеют координаты:
1
30330330
;;
5105
N
−−
и
2
30330330
;;.
5105
N
−
Тогда уравнения касательных плоскостей имеют вид:
30
0,
2
xyz
+−−=
30
0.
2
xyz
+−+=
Пример 4. Составить уравнение касательной плоскости к поверх-
ности, заданной уравнением
,
u
z
v
=
где
,
y
ux
=
vxy
= в точке
(
)
0
1;1.
M
255
Решение. Поверхность задана сложной функцией. Найдем част-
ные производные, используя формулы (18.11) (см. § 18.3):
1
2
1
;
2
y
y
zzuzvu
yx
xuxvxv
vx
−
∂∂∂∂∂
=⋅+⋅=⋅−⋅
∂∂∂∂∂
2
1
ln.
2
y
zzuzvux
xx
yuyvyv
vy
∂∂∂∂∂
=⋅+⋅=⋅⋅−⋅
∂∂∂∂∂
Их значения в точке
(
)
0
1;1
M соответственно равны:
(
)
0
11
1;
22
zM
x
∂
=−=
∂
(
)
0
1
.
2
zM
y
∂
=−
∂
Найдем соответствующее значение
00
:1.
zz
=
Тогда уравнение касательной плоскости:
( )
11
10
22
xy
z
−−
−−−=
или
220.
xyz
−−+=
Пример 5. Записать уравнение нормали к поверхности, заданной
уравнением
sin
yx
ze= в точке
0
1
; 1; .
2
N
e
π
−
Решение. Найдем частные производные и вычислим их в точке N
0
:
sin
cos,
yx
z
eyx
x
⋅
∂
=
∂
(
)
0
0,
zN
x
∂
=
∂
sin
sin,
yx
z
ex
y
⋅
∂
=
∂
(
)
0
1
.
zN
ye
∂
=−
∂
Уравнение нормали в точке N
0
:
1
1
2
1
01
zx
y
e
e
π
−
+
−
==
−
−
или
1
1
2
.
01
zx
y
e
e
π
−
+
−
==
Равенство нулю
(
)
0
zN
x
∂
∂
означает, что касательная плоскость па-
раллельна оси Ох, а нормаль к ней лежит в плоскости
.
2
x
π
=−
Задания
I уровень
1.1. Найдите уравнение касательной плоскости и нормали к
поверхности, заданной функцией
(
)
;
zfxy
= в точке
(
)
0000
;;:
Nxyz
