Майсеня Л.И. Математика в примерах и задачах. Часть 3
Подождите немного. Документ загружается.

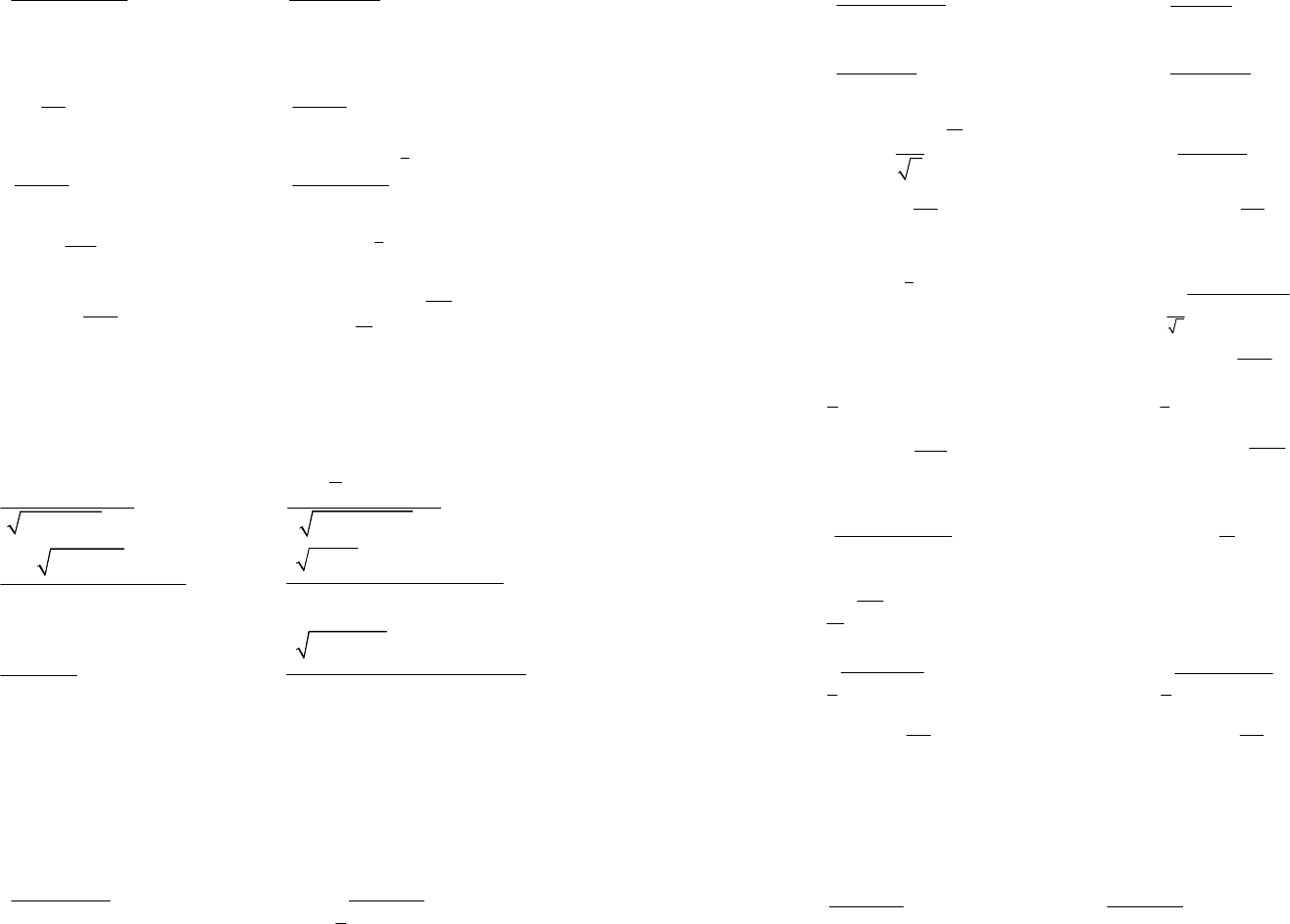
137
11)
2
0
coscos3
lim;
sin3
x
xx
x
→
−
12)
3
0
tg 3
lim.
1cos5
x
xx
x
→
−
1.2. Вычислите предел функции:
1)
2
3
lim1;
5
x
x
x
→∞
+
2)
34
35
lim;
32
x
x
x
x
−
→∞
+
−
3)
2
21
2
2
4
lim;
1
x
x
x
x
−
→∞
+
−
4)
2
2
2
42
lim;
2
x
x
xx
xx
→∞
−+
−
5)
( )
2
4
2
0
lim13;
x
x
x
x
−
→
+ 6)
( )
1
2
0
lim1;
x
x
xx
→
++
7)
( )
1
sin2
0
lim1sin;
x
x
x
→
+ 8)
1
sin
0
lim1ctg.
2
x
x
x
π
→
++
II уровень
2.1. Вычислите предел функции, используя замечательные
пределы:
1)
(
)
2
0
ln1tg 4
lim;
1sin1
x
xx
xx
→
−
+−
2)
( )
tg 3
32
0
3
sin18
lim;
3121
x
x
x
xx
→
−
++−
3)
(
)
( )
23
0
11tg 3sin5
lim;
ln13
x
xx
xx
→
−+
−+
4)
(
)
( )
2
0
121ln1sin3
lim;
tg 2
x
xx
x
→
+−+
5)
3
3
0
lim;
xx
x
xx
ee
−
→
−
−
6)
(
)
(
)
22
3
0
11ln1tg
lim;
sin5
x
xxx
x
→
+−−−
7)
(
)
(
)
(
)
222
limln31ln32;
x
xxx
→∞
−−+
8)
(
)
(
)
(
)
(
)
lim21ln51ln52.
x
xxx
→∞
−+−+
2.2. Вычислите пределы функций, сделав соответствующую
замену переменной:
1)
tg 2
1
lncos2
lim;
(21)
x
x
x
π
π
→
−
2)
2
cos
2
1
lim;
lgsin
x
x
e
x
π
→
−
138
3)
2
tg
3
2
1
lim;
logcos4
x
x
e
x
π
π
→
−
4)
2
2
2
4
lim;
x
x
x
ee
→
−
−
5)
( )
2
5
25
lim;
ln6
x
x
x
→
−
−
6)
(
)
3
1
ln2
lim;
1
x
x
x
→
−
−
7)
3
tg
4
1
limarcsin;
2
x
x
x
π
→
8)
3
2
3
lim;
9
x
x
ee
x
−
→−
−
−
9)
( )
4
1
1
lim32;
x
x
x
x
+
+
→−
+ 10)
( )
1
3
3
lim72;
x
x
x
x
−
−
→
−
11)
( )
2
0
limcos;
x
x
x
→
12)
ln(arcsin/3)
1
32
2
lim;
log8
x
x
e
x
π+
→−
13)
( )
2
3
2
limsin;
tgx
x
x
π
→
14)
( )
8
cos2
4
limsin2;
x
x
x
π
→
15)
( )
1
sin
1
limcos4;
x
x
x
π
π
→
16)
( )
1
ctg
1
limcos2;
x
x
x
π
π
→
17)
(
)
2
tg2
1
ln2cos
lim;
12
x
x
x
π
π
→
+
−
18)
0
1
limsin;
x
x
x
→
19)
3
2
3
limtg ;
2
x
xx
π
π
→
−
20)
(
)
limctg 3;
x
xx
π
π
→
−
21)
2
1cos2
lim;
cos3
x
x
x
π
→
+
22)
6
2sin1
lim;
sin(6)
x
x
x
π
π
→
−
−
23)
( )
1
2
2
lim23;
x
x
x
x
+
−
→
− 24)
( )
1
3
3
lim25.
x
x
x
x
+
−
→
−
III уровень
3.1. Вычислите предел функции:
1)
( )
lim1;
xx
xx
x
aa
a
aa
−
−
→∞
−
>
+
2)
sin
lim;
cos
x
xx
xx
→∞
+
+
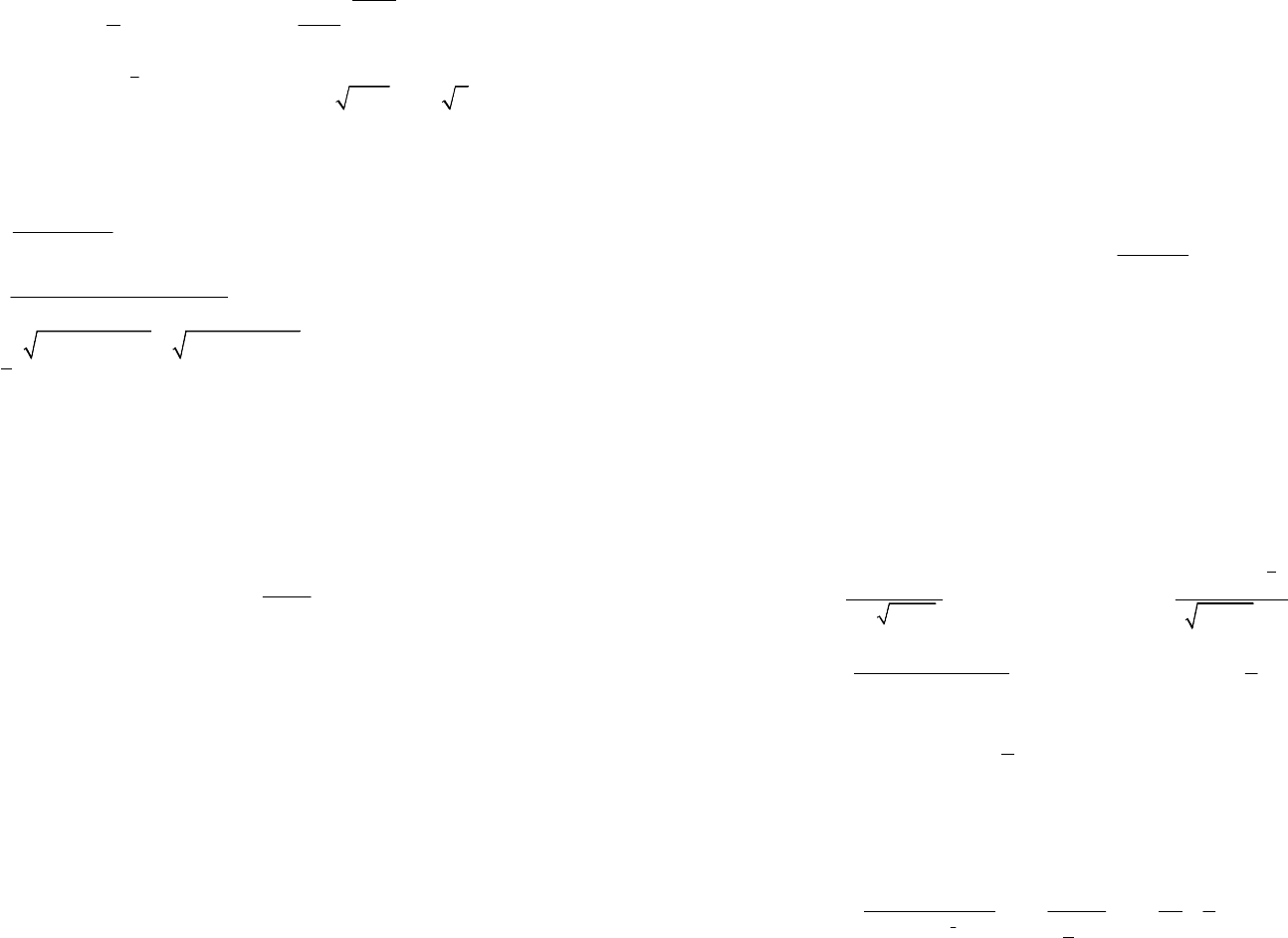
139
3)
2
1
lim1cos;
x
x
x
→∞
−
4)
sin
sin
0
sin
lim;
x
xx
x
x
x
−
→
5)
( )
1
0
limcossin;
x
x
xx
→
+
6)
(
)
limcos1cos.
x
xx
→∞
+−
3.2. Вычислите предел функции, предварительно преобразо-
вав выражение:
1)
ctgtg
lim;
ctgtg
x π
αα
αα
→
+
−
2)
0
sin2sin3sin5
lim;
sin32sin5sin7
x
ααα
ααα
→
++
++
3)
(
)
2
limtg2sin2tg2sin2.
x
xxxx
π
→
+−−
16.3. Эквивалентность бесконечно малых функций
Две функции
(
)
fx
и
(
)
xg называются эквивалентными
бесконечно малыми, при
0
xx
→
(
)
x
→±∞
, если
( )
(
)
()
0
lim1
xx
x
fx
gx
→
→±∞
=
,
это записывают так:
(
)
(
)
~
fxgx
при
0
xx →
(
)
±∞→x .
При вычислении пределов функций в точке и на бесконеч-
ности удобно пользоваться следующей теоремой:
Теорема. Если h(x), f(x) и g(x) – некоторые функции, опреде-
ленные в окрестности точки
0
x (на числовой полуоси) и
(
)
(
)
~
fxgx
при
0
xx →
(
)
±∞→x , то
(
)
(
)
(
)
(
)
(
)
(
)
00
()
limlim.
xxxx
x
hxfxhxgx
→→
→±∞
⋅=⋅ (16.16)
Формула (16.16) показывает, что в произведении можно за-
менять функцию-сомножитель на эквивалентную ей – более
простую для вычисления предела.
140
Таблица эквивалентных бесконечно малых
Пусть
(
)
0
ux
→
, если
0
xx
→
(
)
x
→±∞
. Тогда справедливы
следующие эквивалентности:
(
)
(
)
sin~;
uxux
(16.17)
(
)
(
)
~;
tguxux
(16.18)
(
)
(
)
arcsin~;
uxux
(16.19)
(
)
(
)
~;
arctguxux
(16.20)
()
()
( )
2
cos~1;
2
ux
ux − (16.21)
()
(
)
()
()
( )
()
log1~log;
ln1~;
aa
uxuxe
uxux
+
+
(16.22)
()
()
()
()
1~ln;
1~;
ux
ux
auxa
eux
−
−
(16.23)
( ) ()
1()1~.
uxux
α
α+− (16.24)
Пример 1. Вычислить предел функции в точке, заменяя бесконеч-
но малые эквивалентными им:
1)
(
)
3
0
ln1sin
lim;
112
x
x
x
→
−
−+
2)
(
)
sin
2
5
2
0
tg 1
lim;
121
x
x
xe
x
→
−
+−
3)
(
)
2
2
2
arcsin44
lim;
4
x
xx
x
→−
++
−
4)
1
limarctg.
x
x
x
→∞
Решение. 1) Непосредственное вычисление предела приводит к
неопределенности вида
0
0
. Используем формулу (16.16), а также фор-
мулы (16.22), (16.24), (16.17) таблицы эквивалентных функций.
При этом выполняются условия
20,
x
→
sin0,
x−→ если
0,
x
→
которые являются обязательными для перехода к эквивалентным
функциям. Тогда
(
)
(
)
( )
1
3
000
ln1sin
sin33
limlimlim.
1
22
2
121
3
xxx
x
xx
x
x
x
→→→
+−
−
===
−⋅
−+−
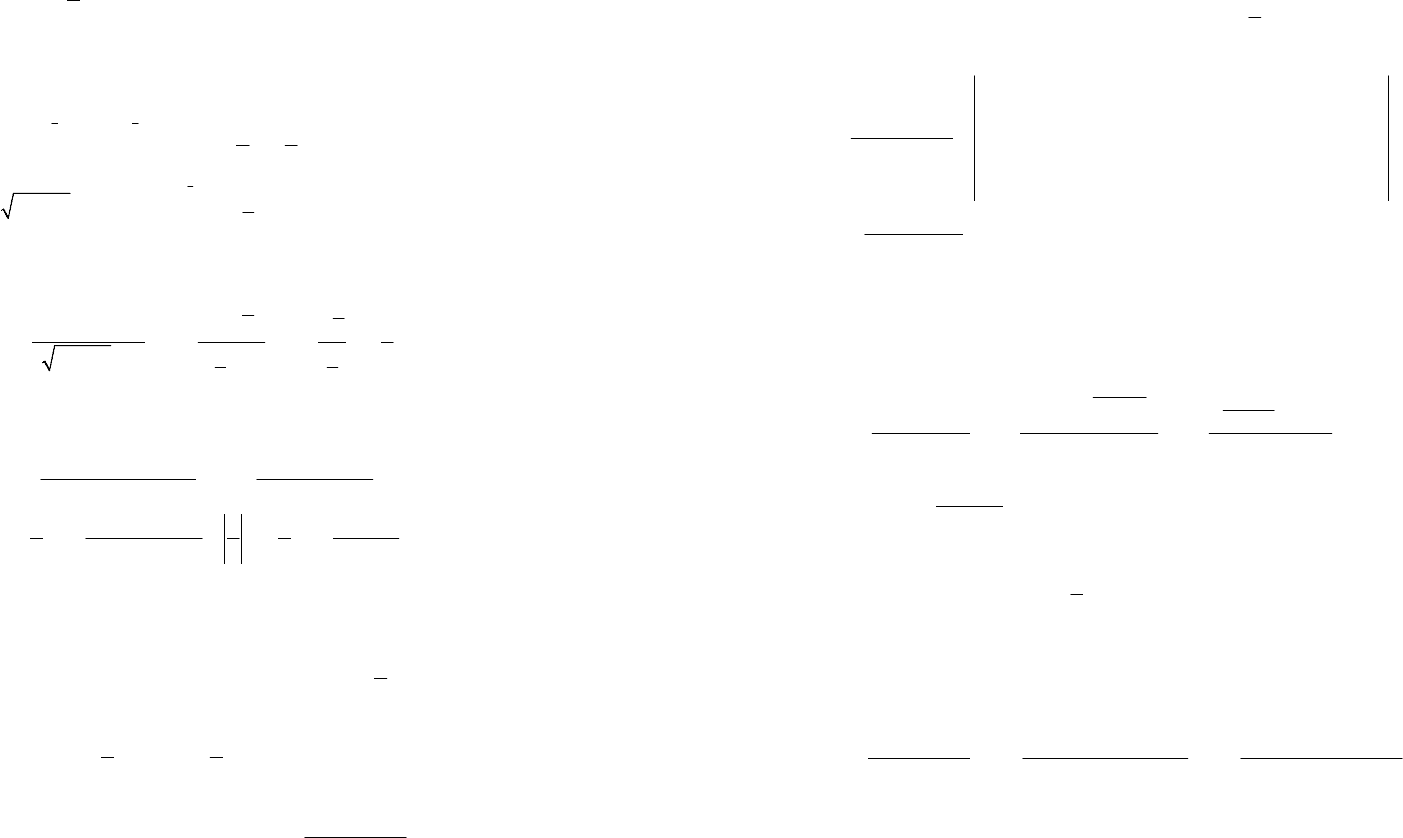
141
Заметим, что решение примера с таким условием уже дано выше
(см. 3-е условие примера 2 из параграфа 16.2).
2) При подстановке
0
x
=
в выражения получаем неопределен-
ность вида
0
0
. Чтобы от нее избавиться, воспользуемся формулами
(16.18), (16.23), (16.24) таблицы эквивалентных бесконечно малых.
Поскольку
0,
x
→
то справедливы эквивалентности:
tg ~;
xx
(
)
22
sinsin
11~sin~;
22
xx
xx
ee
−=−−−−
( )
1
5
5
222
1
121121~2.
5
xxx
+−=+−⋅
Подставив полученные эквивалентные функции вместо соответст-
вующих бесконечно малых, получим:
( )
2
sin
5
2
000
2
1
2
2
22
55
tg15
limlimlim.
4
121
x
xxx
x
x
xe
x
x
→→→
−
−
⋅
−
===−
+−
3) Преобразуем выражение, стоящее под знаком предела, и ис-
пользуем формулу (16.19):
(
)
( )
( )( )
( ) ( )
2
2
2
22
22
22
arcsin44
arcsin2
limlim
22
4
arcsin22
101
limlim0.
42042
xx
xx
xx
x
xx
x
xx
xx
→−→−
→−→−
++
+
==
+−
−
++
=−==−=
++
Использование формулы (16.19) было обосновано тем, что
(
)
20,
uxx=+→ если
2.
x
→−
4) Замечаем, что непосредственное вычисление предела приводит
к неопределенности вида
0.
⋅∞
Вместе с тем,
1
0,
x
→ если
,
x
→∞
а
поэтому можем использовать формулу (16.20). Тогда
11
limarctglim1.
xx
xx
xx
→∞→∞
=⋅=
Пример 2. Вычислить предел:
2
3
3
logcos4
lim
1
tgx
x
x
e
π
π
→
−
несколькими спо-
собами.
142
Решение. 1-й способ. При
3
x
→
получим:
333
logcos4logcos12log10
xππ
===
и
22
tgtg30
111110.
x
eee
ππ
−=−=−=−=
Следовательно, имеем неопределенность вида
0
0
. Сделаем замену
переменной. Введем такое t, чтобы
0,
t
→
если
3:
x
→
( ) ( )
( )
( )
( ) ( )
2
2
3
tg
3
2222
3
tg
0
3,3
30
logcos4
lim
cos4cos43cos412cos4
1
tgtg3tg3tg
logcos4
lim.
1
x
x
t
t
xtxt
xt
x
xttt
e
xttt
t
e
π
π
π
πππππ
πππππ
π
→
→
−==+
→⇒→
==
=+=+=
−
=+=+=
=
−
Далее заменим бесконечно малые в числителе и знаменателе на
эквивалентные по формулам (16.21), (16.23), (16.22), (16.18).
Мы имеем право сделать это, так как для соответствующей функ-
ции u(t) выполняется
()0,
ut → если
0.
t
→
Получаем:
( )
( )
2
2
2
3
3
3
22
tg
000
4
(4)
2
2
log1
log
logcos4
limlimlim
tg
1
t
ttt
t
t
e
t
t
t
e
π
π
π
π
π
π
→→→
−
−
⋅
===
−
( )
( )
2
33
2
0
16
loglim8log.
2
t
t
ee
t
π
π
→
==−
2-й способ. Поскольку при непосредственном вычислении предела
имеем неопределенность вида
0
,
0
то необходимо преобразовать выра-
жение, стоящее под знаком предела. Однако сразу использовать табли-
цу эквивалентности бесконечно малых нельзя, поскольку
cos4
x
π
и
2
tg
x
π
не стремятся к нулю, если
3.
x
→
Используя свойство перио-
дичности тригонометрических функций, получаем:
( )
( )
(
)
(
)
( )
( )
222
3
3
3
tgtg3tg3
333
logcos43
logcos412
logcos4
limlimlim.
1
1
1
xxx
xxx
x
x
x
e
e
e
ππππ
π
ππ
π
−−
→→→
−
−
==
−
−
−
Выражение под знаком предела преобразовано таким образом, что
(
)
430
xπ
−→
и
(
)
30,
xπ −→ если
3.
x
→
Поэтому можно использо-
вать формулы эквивалентности (16.21), (16.23), (16.22), (16.18). В ре-
зультате получаем:
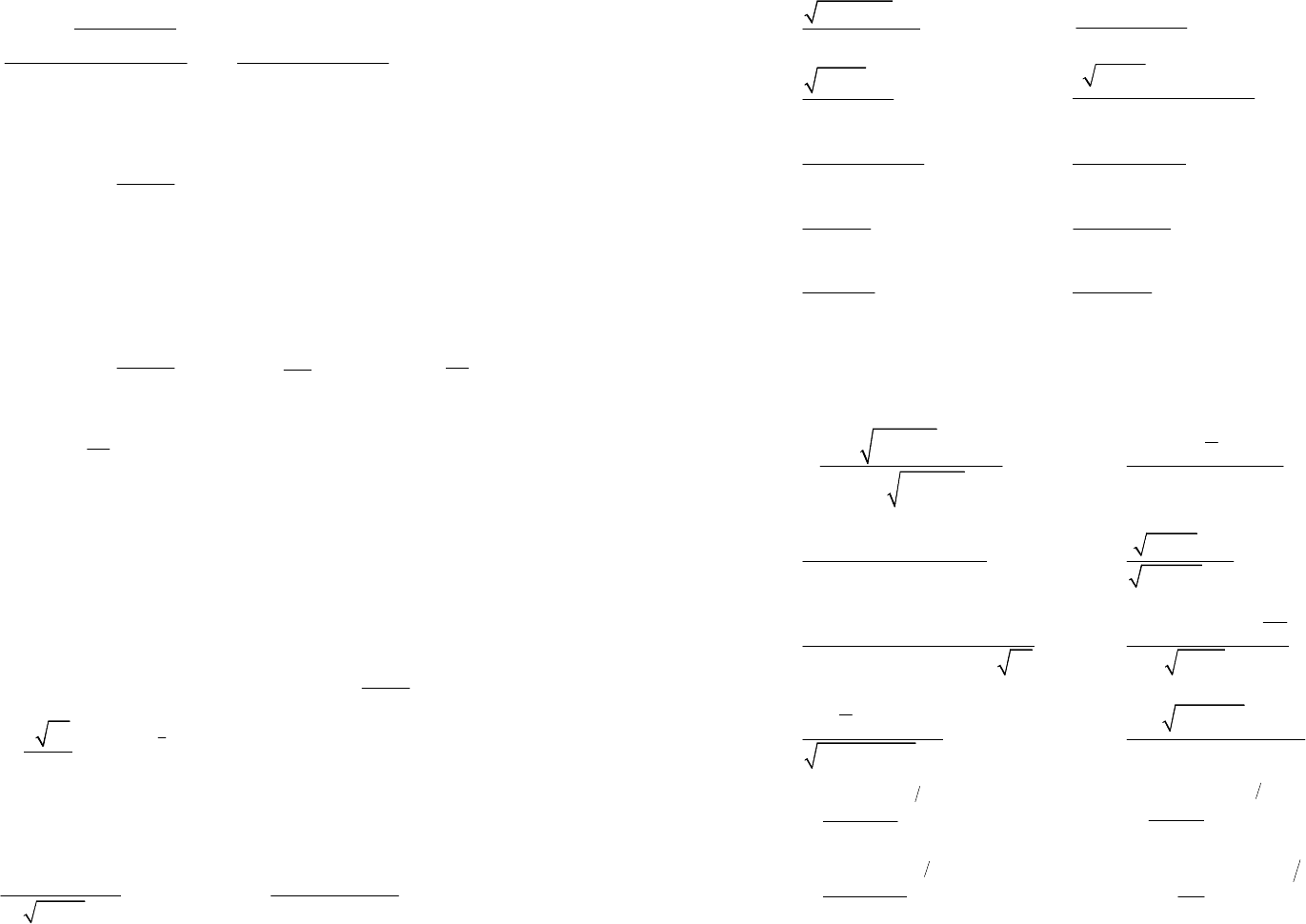
143
( )
( )
( )
( )
( )
2
2
3
2
2
3
3
22
2
33
163
log1
2
83log
limlim8log.
tg3
3
xx
x
xe
e
x
x
π
π
π
π
→→
−
−
−−
==−
−
−
Пример 3. Вычислить предел функции, заменяя бесконечно малые
эквивалентными,
( )
( )
2
3
3
arcsin
0
lim1ln1.
xx
x
x
→
−+
Решение. Непосредственное вычисление предела приводит к не-
определенности вида
0.
∞
Используем формулы (16.19) и (16.22) таб-
лицы эквивалентных функций.
При этом выполняется условие
3
0,
x → если
0,
x
→
которое яв-
ляется обязательным для перехода к эквивалентным функциям. Тогда
( )
( )
( ) ( )
( )
23
2
33
3
333
arcsin
000
lim1ln1lim1lim1.
xxx
xx
xxx
xxx
−
−
⋅
→→→
−+=−=+−
Используя далее вторую формулу из (16.12), получаем:
( )
( )
3
0
3
lim(3)
33
0
lim1.
x
x
x
xee
→
−
−
−
−
→
+−==
Задания
I уровень
1.1. Докажите, что функции
(
)
x
α и
(
)
x
β являются эквива-
лентными бесконечно малыми при
0:
x
→
1)
(
)
(
)
352
23,;
xxxxx
αβ=+= 2)
() ()
10
5
3
7
,;
1
x
xxx
x
αβ==
+
3)
() ()
1
3
2
2
3
,;
1
x
xxx
x
αβ==
−
4)
(
)
2
sin2,().
xxxx
αβ
==
1.2. Вычислите предел функции, заменяя бесконечно малые
эквивалентными:
1)
( )
( )
2
0
arcsin4
lim;
151
x
x
xx
→
+−
2)
(
)
(
)
( )( )
0
5121
lim;
3161
xx
xx
x→
−−
−−
144
3)
4
0
1sin31
lim;
sin2
x
x
x
→
+−
4)
x
ee
xx
x
sin2sin
0
lim
−
→
;
5)
2
0
11
lim;
x
x
x
→
+−
6)
(
)
( )
2
0
121ln1
lim;
tg 2
x
xx
x
→
+−+
7)
0
sin2ar
сtg7
lim;
tg5arcsin3
x
xx
xx
→
8)
23
0
52
lim;
arctg 27
xx
x
xx
→
−
−
9)
2
2
0
lim;
xx
x
ee
xtgx
→
−
+
10)
23
2
0
lim;
arctg
xx
x
ee
xx
→
−
−
11)
7
0
42
lim;
tg3
xx
x
xx
→
−
−
12)
0
1cos5
lim.
tg2
x
x
xx
→
−
II уровень
2.1. Вычислите предел функции, используя эквивалентность
бесконечно малых:
1)
( )
( ) ( )
3
5
0
2
3
11
lim;
111
x
x
xx
→
+−
++−
2)
2
23
0
arcsin
3
lim;
arctg34
x
x
x
xxx
→
+
−+
3)
(
)
23
23
0
ln1234
lim;
ln(127)
x
xxx
xxx
→
+−+
−+−
4)
3
4
0
832
lim;
1652
x
x
x
→
+−
+−
5)
( )
( )
22
5
26
0
17
lim;
sin3tg
x
x
ex
xxx
π
→
−−
++−
6)
3
2
3
3
0
2
(1)arctg
2
lim;
11
xx
x
x
e
x
−
→
−
−−
7)
( )
3
3
32
0
sin18
3
lim;
121
tgx
x
x
xx
→
−
++−
8)
(
)
( )
23
0
11tg2sin6
lim;
ln13
x
xx
xx
→
−+
−+
9)
( )
( )
4
0
ln1
lim;
3
xx
x
x
x
+
→
+
10)
(
)
(
)
3
382
2
0
1
lim;
xx
x
x
e
x
++
→
−
11)
( )
( )
23
2
2
0
lim;
ln1
x
x
x
x
+
→
+
12)
(
)
1
0
5
limtg.
4
x
ex
x
x
π
−
→
−

145
2.2. Вычислите предел функции:
1)
( )
( )
2
1
2
sin1cos
lim;
31
x
x
x
x
π
→
−
−
2)
3
2
1
1ln1
lim;
1cos
x
x
x
π
→
+−
+
3)
2
cos
2
1
lim;
lgsin
x
x
e
x
π
→
−
4)
(
)
2
2
1
ln33
lim;
76
x
xx
xx
→
−+
−+
5)
( )
3
22
3
lim;
ln1tg
x
x
x
π
π
→
−
+
6)
(
)
sin2
ln2cos
lim;
(31)
x
x
x
π→
+
−
7)
( )
2
4
lnsin4
lim;
4x
x
x
π
π→ −
8)
sin
3
2
21
lim;
ln(65)
x
x
xx
π
→
−
−+
9)
1
2
3
1
363
lim;
1
x
x
x
x
+
→
+−
−
10)
lncos4
lim.
lncos2
x
x
x
π→
III уровень
3.1. Вычислите предел функции с помощью таблицы экви-
валентности бесконечно малых двумя способами (производя за-
мену переменной и без замены переменной):
1)
3
4
3
sin7
lim;
sin8
x
x
xx
π
π
→
2)
coscos3
2
lnsin
lim;
xx
x
x
ee
π
→
−
3)
sin
1
2
lg2sin
lim;
1
x
x
x
e
π
π
→−
+
−
4)
3
2
2
1sin
lim.
cos
x
x
x
π→
−
3.2. Вычислите предел функции несколькими способами:
1)
2
limtg;
2
x
xx
π
π
→
−⋅
2)
(
)
222
2
limtg2sin3sin4sin6sin2.
x
xxxxx
π
→
++−++
3.3. Вычислите предел функции:
146
1)
( )
( )
ln32
ln2
1
21
lim;
x
x
x
x
x
+
−
→
−
2)
( )
1cos2
limctg;
4
x
x
x
π→
3)
( )
1
1
tg9
lim;
sin4
xx
x
x
x
π
π
+
→
4)
22
sinsin
lim.
xa
xa
xa
xa
→
−
−
16.4. Односторонние пределы. Асимптоты
графика функции
Левой (правой) полуокрестностью точки х
0
называется
произвольный интервал
(
)
0
,
а x
(
)
(
)
0
,,
xb
где
0
а x
<
(
)
0
bx
> слева
(справа).
Число А называется пределом слева (справа) функции f(x) в
точке х
0
, если функция f(x) определена в некоторой левой (пра-
вой) полуокрестности точки
0
x
и если для любого
0
ε
>
суще-
ствует
(
)
0
δδε
=>
такое, что для всех x, удовлетворяющих ус-
ловию
(
)
0000
,
xxxxxx
δδ
−<<<<+ выполняется неравенство
(
)
.
fxA
ε
−<
В этом случае пишут:
() ()
00
00
limlim.
xxxx
А fxAfx
→−→+
==
Пределы слева и справа называются односторонними пре-
делами. Если
0
0,
x
=
то односторонние пределы обозначают
(
)
0
lim,
x
fx
→−
(
)
0
lim.
x
fx
→+
Функция f(x) имеет предел в точке
0
x
тогда и только тогда,
когда в этой точке существуют оба односторонних предела, рав-
ных между собой.
В этом случае их общее значение является пределом функ-
ции f(x) в точке
0
:
x
(
)
(
)
(
)
000
00
limlimlim.
xxxxxx
fxfxfx
→→+→−
==
Асимптота графика функции
(
)
yfx
= – это прямая ли-
ния, к которой неограниченно приближается график данной

147
функции, когда его точка неограниченно удаляется от начала
координат.
Различают горизонтальную, вертикальную и наклонную
асимптоты.
Прямая
xa
=
называется вертикальной асимптотой графи-
ка функции
(
)
,
yfx
= если
(
)
0
lim
xa
fx
→−
=±∞
или
(
)
0
lim.
xa
fx
→+
=±∞
В случае вертикальной асимптоты
xa
=
функция является
бесконечно большой в точке
.
xa
=
Прямая y = b называется горизонтальной асимптотой
графика функции
(
)
,
yfx
= если
(
)
lim.
x
fxb
→±∞
=
Вертикальные асимптоты могут существовать у функций,
которые определены не на всей числовой прямой, т. е. имеют
разрыв второго рода.
Если областью определения функции является вся числовая
прямая, то у функции нет вертикальных асимптот.
Прямая
ykxb
=+
называется наклонной асимптотой гра-
фика функции
(
)
,
yfx
= при
,
x
→+∞
если
(
)
(
)
(
)
lim0.
x
fxkxb
→+∞
−+=
Для нахождения коэффициентов k и b применяют следую-
щие формулы:
(
)
lim,
x
fx
k
x
→±∞
= (16.25)
(
)
(
)
lim.
x
bfxkx
→±∞
=− (16.26)
Если хотя бы один из пределов (16.25), (16.26) равен
∞
или
не существует, то у функции наклонных асимптот нет.
Если
0,
k
=
0,
b
≠
то прямая
yb
=
является горизонтальной
асимптотой. Заметим, что наклонных асимптот у функции мо-
жет быть не больше двух, а вертикальных может быть сколько
угодно.
Пример 1. Найти односторонние пределы функции f(x) в точке х
0
:
1)
()
1
2
,
x
fx е
−
=
0
2;
x
=
2)
()
{
2
sin,0;
(1),0;
xx
fx
xx
≤
=
+>
0
0.
x
=
Решение. 1) Вычислим пределы функции в точке
0
2
x
=
слева и
148
справа, т. е.
1
2
20
lim
x
x
е
−
→−
и
1
2
20
lim.
x
x
e
−
→+
Если
20,
x
→−
то
20,
x
−→−
значит
1
.
2x
→−∞
−
Получаем
1
2
20
lim0.
x
x
e
−
→−
=
Если
20,
x
→+
то
20,
x
−→+
значит
1
.
2x
→+∞
−
Получаем
1
2
20
lim.
x
x
e
−
→+
=+∞
2) При
0
x
≤
функция задана формулой
(
)
sin.
fxx
= Поэтому
(
)
0
0
limlimsin0.
x
x
fxx
→−
→−
==
При
0
x
>
функция задана формулой
() ( )
2
1
fxx=+ т. е.
() ( )
2
00
limlim11.
xx
fxx
→+→+
=+=
Значит
(
)
2
00
limlim(1)1.
xx
fxx
→+→+
=+=
Пример 2. С помощью односторонних пределов показать, что
функция
()
2
x
fx
xx
=
+
не имеет предела в точке
0
0.
x
=
Решение. При
0
x
<
имеем
xx
=−
и функция принимает вид:
()
( )
2
1
.
11
xx
fx
xxx
xx
−−−
===
++
+
Поэтому
()
00
11
limlim1.
110
xx
fx
x
→−→−
−
==−=−
++
При
0
x
>
имеем
xx
=
и функцию
()
( )
1
.
11
x
fx
xxx
==
++
Поэтому
()
00
11
limlim1.
110
xx
fx
x
→+→+
===
++
Получим, что оба односторонних предела функции в точке
0
0
x
=
существуют, однако они различны, поэтому
2
0
lim
x
x
xx
→
+
не существует.
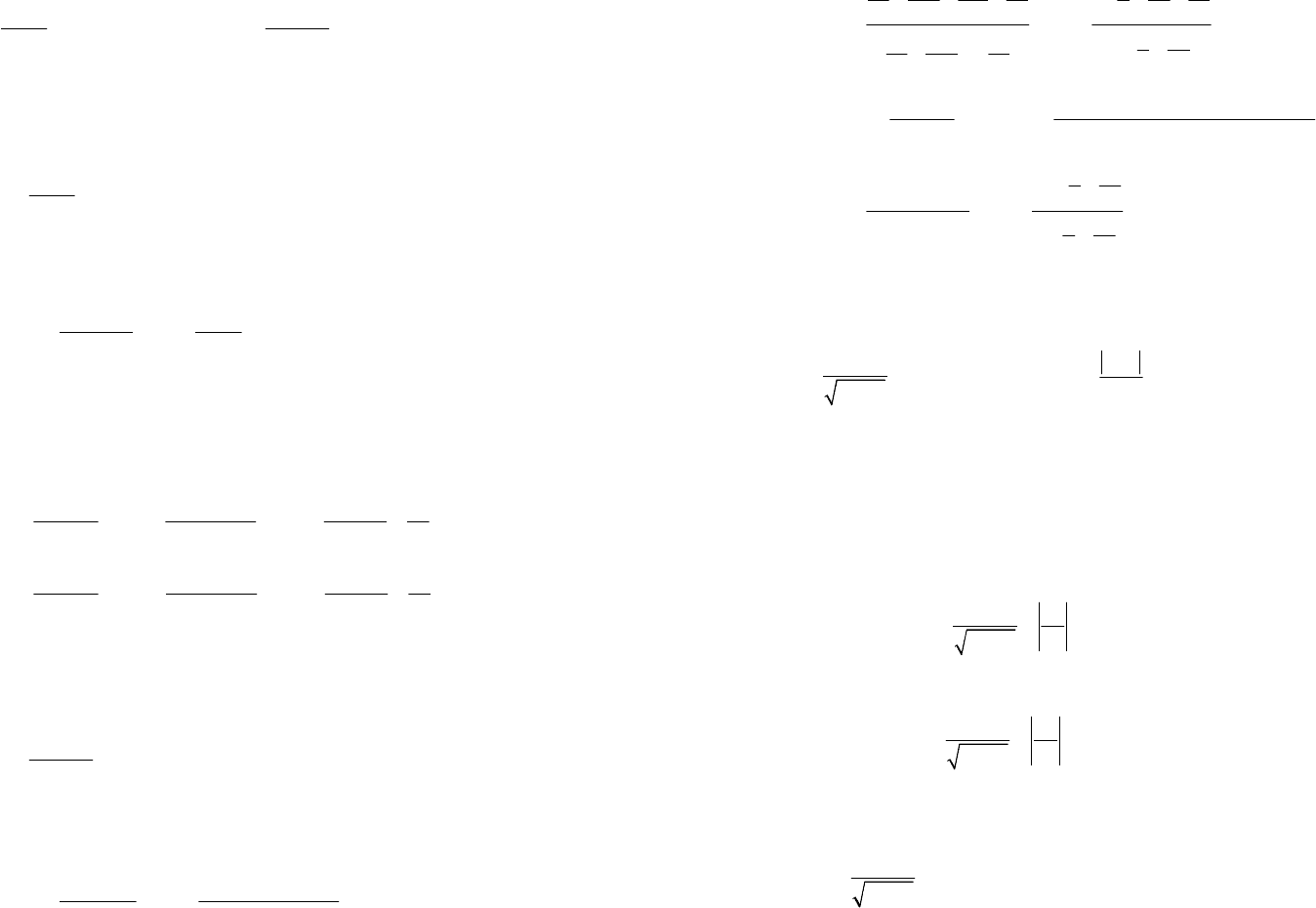
149
Пример 3. Найти асимптоты графика функции:
1)
2
;
1
x
y
x
=
+
2)
( )
( )
3
2
2
.
2
x
y
x
+
=
−
Решение. 1) Вертикальных асимптот данная функция не имеет,
потому что она определена для любых
(
)
;.
x
∈−∞+∞
Для того чтобы
найти горизонтальные асимптоты, надо рассмотреть пределы функции
на бесконечности:
2
lim0.
1
x
x
x
→±∞
=
+
Получили, что
0
y
=
– горизонтальная асимптота (ось 0x).
Будем искать наклонные асимптоты в виде функции
.
ykxb
=+
Согласно формулам (16.25) и (16.26), вычисляем:
( )
22
1
limlim0.
1
1
xx
x
k
x
xx
→±∞→±∞
===
+
+
Так как
0,
k
=
значит наклонных асимптот у графика нет.
2) Так как при
2
x
=
функция не определена, рассмотрим
(
)
20
lim
x
fx
→−
и
(
)
20
lim.
x
fx
→+
Вычисляем:
( )
( )
( )
( )
( )
( )
333
222
202020
220240
64
limlimlim;
0
22020
xxx
x
x
→−→−→−
+−+−
====+∞
−−−−
()
()
()
()
()
333
222
202020
220240
64
limlimlim.
0
0
2202
xxx
x
x
→+→+→+
++++
====+∞
−+−
Поэтому прямая
2
x
=
является вертикальной асимптотой графика
функции.
Ищем горизонтальную асимптоту.
Вычисляем
( )
( )
3
2
2
lim,
2
x
x
x
→±∞
+
=∞
−
это означает, что горизонтальных асимптот нет.
Выясним наличие наклонных асимптот. По формулам (16.25) и
(16.26) находим:
( )
( )
3
32
232
2
6128
limlim
44
2
xx
x
xxx
k
xxx
xx
→±∞→±∞
+
+++
===
−+
−
150
32
333323
32
2
333
61286128
1
limlim1.
44
4
1
4
xx
xxx
x
xxxxxx
xxx
x
x
xxx
→±∞→±∞
++++++
===
−+
−+
( )
( )
3
3232
22
2
612844
limlim
44
2
xx
x
xxxxxx
bx
xx
x
→±∞→±∞
+
+++−+−
=−==
−+
−
2
2
2
2
88
10
1088
limlim10.
44
44
1
xx
xx
x
x
xx
x
x
→±∞→±∞
++
++
===
−+
−+
Приходим к выводу, что
10
yx
=+
– наклонная асимптота.
Пример 4. Найти асимптоты графика функции:
1)
2
2
12
;
4
x
y
x
−
=
−
2)
1
.
1
x
y
x
−
=
+
Решение. 1) Областью определения D(y) функции является то
множество, на котором выполняется неравенство
2
40.
x
−>
Решив
последнее неравенство, получим что
(
)
(
)
();22;.
Dy
=−∞−∪+∞
Определим вертикальные асимптоты графика функции. Рассмот-
рим поведение функции в окрестности точки
2.
x
=−
Функция опреде-
лена только в левой полуокрестности этой точки, поэтому вычисляем
левосторонний предел:
()
2
2
20
20
127
limlim.
0
4
x
x
x
fx
x
→−−
→−−
−−
===−∞
+
−
В окрестности точки
2
x
=
функция определена только справа, по-
этому в этой точке можем рассмотреть правосторонний предел:
()
2
2
20
20
127
limlim.
0
4
x
x
x
fx
x
→+
→++
−−
===−∞
+
−
.
Приходим к заключению, что прямые
2
x
=−
и
2
x
=
являются
вертикальными асимптотами графика функции. Горизонтальных асимп-
тот нет, так как
2
2
12
lim.
4
x
x
x
→±∞
−
=∞
−
Найдем наклонные асимптоты:
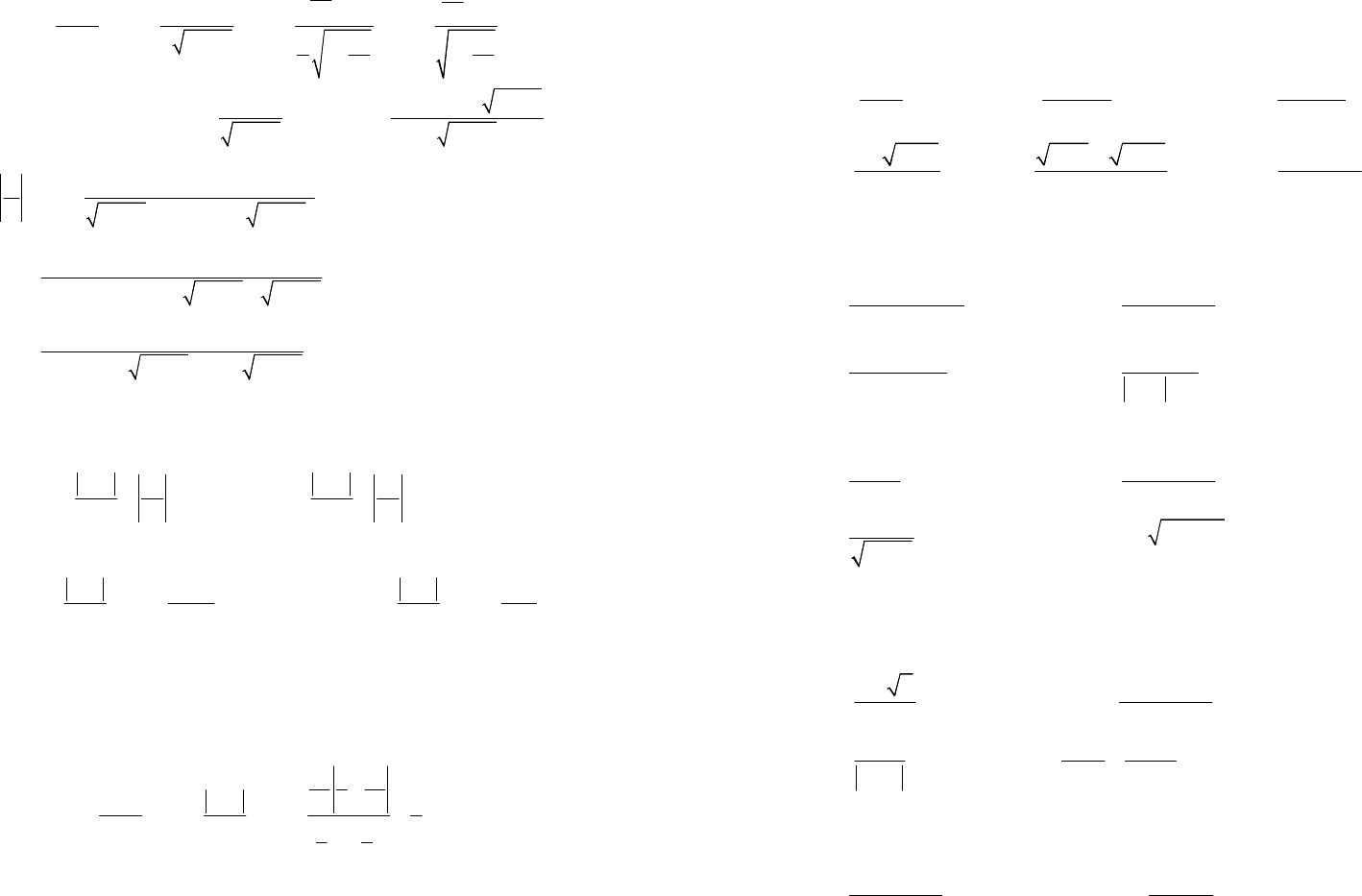
151
()
2
2
2
2
22
1
1
2
2
12
limlimlimlim2.
44
4
11
xxxx
fx
x
x
x
k
x
x
xx
x
xx
→±∞→±∞→±∞→±∞
−
−
−
=====−
−
−−
()
( )
222
22
121224
limlim2lim
44
xxx
xxxx
bfxxx
xx
κ
→±∞→±∞→±∞
−−+−
=−=+==
−−
()()
(
)
()
2
222
222
2442
2222
1244
lim
41224
144416
lim
24244
x
x
xxx
xxxx
xxxx
xxxxx
→±∞
→±∞
−−−
∞
===
∞
−−−−
−+−+
==
−−−−+−
2
3222
121
lim0.
22484
x
x
xxxxx
→±∞
+
==
−−−++−
Таким образом,
2
yx
=−
– наклонная асимптота.
2) Функция определена всюду на числовой прямой, кроме точки
1,
x
=−
т. е.
(
)
(
)
();11;.
Dy
=−∞−∪−+∞
Рассмотрим
10
1
2
lim,
10
x
x
x
→−−
−
==−∞
+−
10
1
2
lim.
10
x
x
x
→−+
−
==+∞
++
Прямая
1
x
=−
– вертикальная асимптота.
Найдем горизонтальные асимптоты:
1
1
1
limlim1,
11
xx
x
x
x
xx
→−∞→−∞
<
−
−+
==−
++
1
1
1
limlim1.
11
xx
x
x
x
xx
→+∞→+∞
>
−
−
==
++
Получаем, что прямая
1
y
=−
является горизонтальной асимпто-
той при
(
)
1,
xx→−∞< а прямая
1
y
=
– горизонтальная асимптота
при
(
)
1.
xx
→+∞>
Ищем наклонные асимптоты:
()
22
1
111
1
1
1
0
limlimlim0.
1
xxx
x
xx
x
xx
x
fx
k
xx
→±∞→±∞→+∞
−
+
−
=====
Наклонных асимптот нет.
152
Задания
I уровень
1.1. Вычислите односторонние пределы функции:
1)
10
3
lim;
1
x
x
x
→±
+
−
2)
( )
2
20
21
lim;
2
x
x
x
→±
+
−
3)
( )
3
30
1
lim;
3
x
x
→−±
+
4)
0
14
lim;
x
x
x
→±
++
5)
3
2
0
14
lim;
x
xx
x
→±
+++
6)
2
20
2
lim.
1
x
xx
x
→−±
+−
−
1.2. Определите, сколько вертикальных асимптот имеет гра-
фик функции
(
)
,
yfx
= найдите их:
1)
( )( )
1
;
21
y
xx
=
−+
2)
2
sin
;
69
x
y
xx
=
−+
3)
(
)
3
log2
;
5
x
y
x
−
=
−
4)
4
.
12
x
y
x
+
=
+−
1.3. Найдите асимптоты кривых:
1)
21
;
1
x
y
x
+
=
−
2)
2
43
;
1
xx
y
x
−+
=
−
3)
3
3
;
1
x
y
x
−
=
+
4)
3
2
12.
yxx
=−−
II уровень
2.1. С помощью односторонних пределов определите, имеет ли
функция предел в точке. В случае существования вычислите его:
1)
2
4
2
lim;
16
x
x
x
→+
−
−
2)
2
2
1
1
lim;
43
x
x
xx
→
−
−+
3)
2
3
lim;
2
x
x
x
→−
+
4)
3
2
13
lim.
2
8
x
x
x
→
−
−
−
2.2. Среди данных функций выберите те, которые имеют
вертикальные асимптоты (ответ подтвердите доказательством):
1)
2
56
;
1
xx
y
x
−−
=
+
2)
2
2
2
;
4
xx
y
x
−
=
−
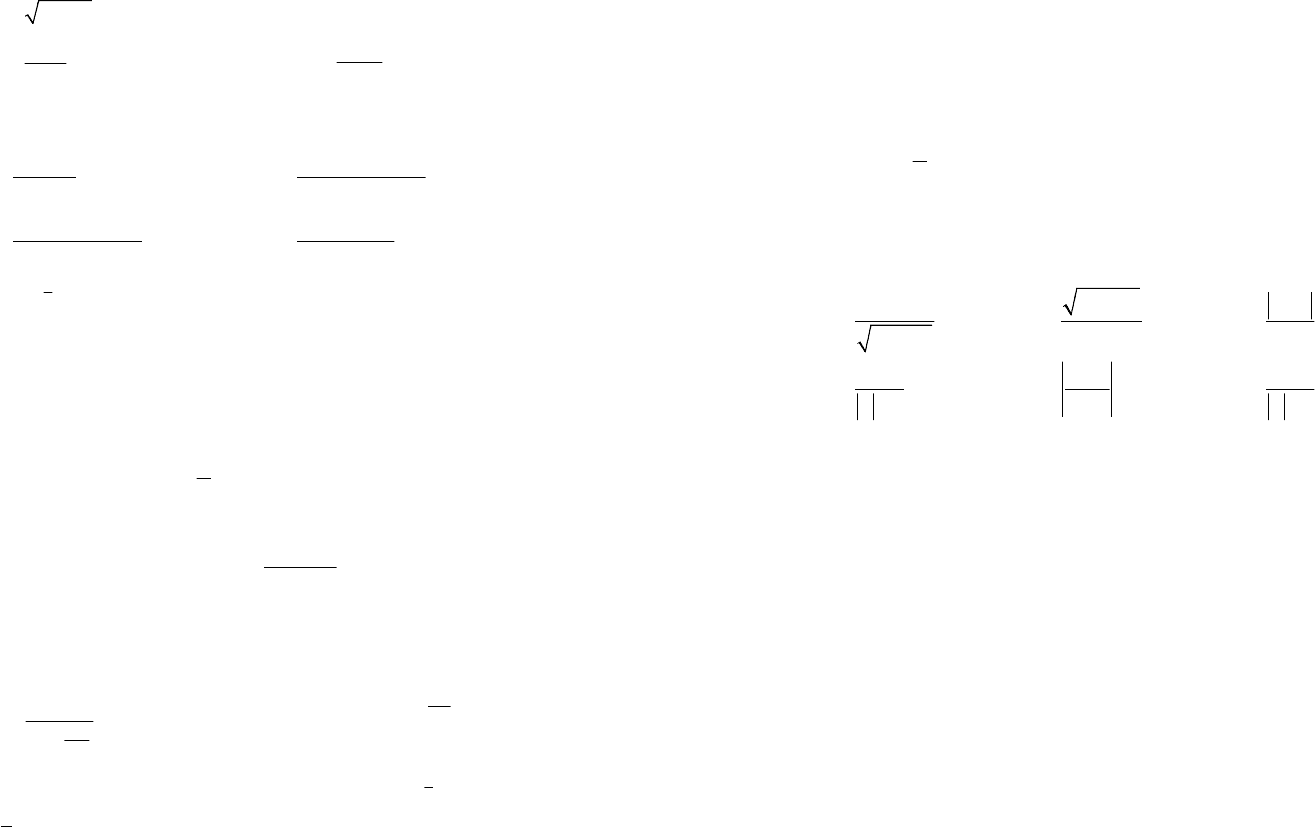
153
3)
1,
если 1,
1
,
если 1;
1
xx
y
x
x
−+≤
=
>
+
4)
2
27,
если 2,
1
,
если 2.
2
xx
y
x
x
−≤
=
>
−
2.3. Найдите асимптоты кривых:
1)
2
21
;
4
x
y
x
+
=
−
2)
32
2
2
;
33
xxx
y
x
+−+
=
−
3)
32
2
2
;
33
xxx
y
x
+−+
=
−
4)
2
2
1
;
56
x
y
xx
−
=
−+
5)
1
2
;
x
yxe
= 6)
31
;
x
yxe
+
=
7)
(
)
2
ln4;
yx
=− 8)
(
)
2
ln26.
yxx=−+
2.4. Докажите, что заданные прямые являются асимптотами
графика функции
():
yfx
=
1)
0
x
=
для функции
2
1
4;
yx
х
=+
2)
yx
π
=±
для функции
2arctg;
yxx
=−
3)
2,0
xy
==
для функции
( )
2
3
4.
2
x
y
x
−
=
−
III уровень
3.1. Вычислите односторонние пределы функции в точке:
1)
1
20
2
1
lim;
13
x
x
→±
−
+
2)
1
1
10
lim12;
x
x
−
→±
−
3)
0
6
limarctg3;
x
x
π
π
→±
4)
1
2
0
limlog;
x
x
e
→±
5)
(
)
3
20
limarcsinlog2;
x
x
→−
−
6)
(
)
1
23
10
limloglog1.
x
x
−
→±
+
3.2. Вычислите односторонние пределы функции
(
)
yfx
= в
точке
0
:
x
154
1)
1, åñëè 0,
sin,åñëè 0,
xx
y
xx
−<
=
≥
0
0;
x
=
2)
2, åñëè 1,
ln,åñëè 1,
x
y
xx
<
=
≥
0
1;
x
=
3)
( )
2
arctg,åñëè 3,
3
3,åñëè 3,
x
x
y
xx
≤
=
−>
0
3.
x
=
3.3. Определите асимптоты графика функции:
1)
2
2
105
;
19
x
y
x
−
=
−
2)
2
16
;
2
x
y
x
−
=
+
3)
( )
2
1
3;
1
x
yx
x
−
=+
−
4)
1
;
1
x
y
x
+
=
+
5)
1
;
3
x
y
x
+
=
+
6)
1
.
1
y
x
=
−
16.5. Непрерывность функции. Классификация
точек разрыва
Функция f(x) называется непрерывной в точке
0
,
x
если она
определена в этой точке и некоторой ее окрестности и если вы-
полняется условие
(
)
(
)
0
0
lim.
xx
fxfx
→
= (16.27)
Если функция
(
)
yfx
= непрерывна в каждой точке некото-
рого промежутка, то говорят, что функция непрерывна на этом
промежутке.
Существуют и другие определения непрерывности функции
в точке. Функция f(x) называется непрерывной в точке, если она
определена в этой точке и некоторой ее окрестности и если бес-
конечно малому приращению аргумента соответствует беско-
нечно малое приращение функции в этой точке:
(
)
0
0
lim0.
x
fx
∆→
∆=
(16.28)
Непрерывность функции в точке определяется также на ос-
нове односторонних пределов.
155
Функция f(x) называется непрерывной в точке
0
,
x
если она
определена в этой точке и некоторой ее окрестности и если су-
ществуют односторонние пределы (конечные) такие, что
(
)
(
)
(
)
00
0
00
limlim.
xxxx
fxfxfx
→−→+
== (16.29)
Свойства непрерывных функций
1. Если функции f(x) и g(x) непрерывны в точке х
0
, то их
сумма
(
)
(
)
fxgx
+ также есть непрерывная функция в точке х
0
.
Это свойство справедливо для любого конечного количества
слагаемых.
2. Произведение конечного количества непрерывных функ-
ций есть функция непрерывная.
3. Частное двух непрерывных функций есть функция непре-
рывная, если знаменатель в рассматриваемой точке не обраща-
ется в нуль.
4. Если функция f(x) непрерывна в точке х
0
и
0
()0,
fx
≠
то
значения функции f(x) в некоторой окрестности точки х
0
имеют
тот же знак, что и функция
(
)
0
.
fx
5. Если функция
(
)
yx
ϕ= непрерывна в точке х
0
и принимает
в этой точке значение
(
)
00
,
ux
ϕ= а функция f(u) непрерывна в
точке
0
,
u
то сложная функция
(
)
(
)
fx
ϕ в точке х
0
непрерывна.
6. Всякая элементарная функция непрерывна в каждой точ-
ке, в которой она определена.
7. Если непрерывная на некотором отрезке функция f(x)
принимает на его концах значения разных знаков, то на этом от-
резке найдется хотя бы одна точка, в которой функция
(
)
0.
fx
=
8. Если функция f(x) непрерывна в точке х
0
, то операции вы-
числения предела в этой точке и функции f переставимы, т. е.
(
)
(
)
00
limlim.
xxxx
fxfx
→→
= (16.30)
На свойстве 8 (равенство (16.30)) и было основано непо-
средственное вычисление предела функции в случае отсутствия
неопределенности (см. § 16.1–16.4).
Если нарушается хотя бы одно условие, указанное в опреде-
лении непрерывности, то точка х
0
называется точкой разрыва
функции.
156
Классификацию точек разрыва дают в зависимости от того,
какое условие последнего определения непрерывности, в том
числе равенства (16.29), нарушено.
Точки разрыва I рода
1. Если существуют односторонние пределы в точке х
0
(ко-
нечные) и
(
)
(
)
(
)
00
0
00
limlim,
xxxx
fxfxfx
→−→+
=≠
то точка х
0
называется точкой устранимого разрыва.
2. Если существует односторонние пределы в точке х
0
(ко-
нечные) и
(
)
(
)
00
00
limlim,
xxxx
fxfx
→−→+
≠ (16.31)
то х
0
– точка разрыва, который называется скачок.
В случае устранимого разрыва функцию можно доопреде-
лить в точке х
0
значением функции f(x) и она станет непрерыв-
ной. В случае скачка это сделать невозможно.
Точки разрыва II рода
1. Если
(
)
0
0
lim
xx
fx
→−
=±∞
или
(
)
0
0
lim,
xx
fx
→+
=±∞
то х
0
– точка
разрыва, который называется бесконечный скачок. В этом слу-
чае прямая
0
xx
=
является вертикальной асимптотой.
2. Если односторонние пределы в точке х
0
не существуют
(не определены), то х
0
– точка неопределенности.
Для того чтобы исследовать функцию на непрерывность,
необходимо ответить на вопросы:
1) где функция непрерывна;
2) какие точки являются точками разрыва;
3) какой характер разрыва в этих точках?
Пример 1. Пользуясь определением непрерывности доказать, что
функция
(
)
2
1
fxxx
=−+
непрерывна всюду на R.
Решение. Докажем непрерывность этой функции в произвольной
точке
0
x
∈
R
.
Пусть
x
∆
– приращение аргумента в точке х
0
. Соответствующее
приращение функции имеет вид:
( ) ( ) ( ) ( ) ( )
(
)
2
2
0000000
11
fxfxxfxxxxxxx
∆=+∆−=+∆−+∆+−−+=
