Майсеня Л.И. Математика в примерах и задачах. Часть 3
Подождите немного. Документ загружается.


97
(
)
( )
1212
12
12
,,
(,),
,
rraa
dLL
aa
−
= (15.18)
где
1
r
и
2
r
– радиус-векторы точек
1111
(,,)
Mxyz
и
2222
(,,),
Mxyz
принадлежащих прямым L
1
и L
2
соответственно,
а векторы
1
a
и
2
a
– направляющие векторы этих прямых.
Пример 1. Составить канонические уравнения прямой, проходя-
щей через:
1) точку
0
(2, 1, 5)
M − параллельно вектору
(1, 3, 4);
a =−
2) две заданные точки
1
(1, 5, 1)
M и
2
(4, 6, 9).
M
Решение. 1) Пусть
(,,)
Mxyz
– произвольная точка искомой пря-
мой. Тогда ,||
0
aMM т. е. их координаты пропорциональны.
),5,1,2(),,(
0000
−−+=−−−= zyxzzyyxxMM )4 ,3 ,1( −=a . Со-
гласно (15.14) получаем уравнения
215
,
134
xyz
+−−
==
−
которые и представляют собой канонические уравнения прямой.
2) Пусть
(,,)
Mxyz
– произвольная точка прямой. Тогда, исполь-
зуя уравнение (15.15) для нашего случая, имеем:
1
(1,5,1),
MMxyz
=−−−
12
(41, 65, 91)(3, 1, 8),
MM =−−−= откуда
151
.
318
xyz
−−−
==
Это и есть искомый результат.
Пример 2. Записать канонические уравнения прямой, заданной
системой уравнений двух плоскостей
324110,
2310.
xyz
xyz
++−=
+−−=
Решение. Для перехода к каноническим уравнениям прямой
обычно поступают следующим образом. Подбирают какую-либо точку
0
,
ML
∈
фиксируя числовое значение одной из координат и решая сис-
тему двух линейных уравнений с двумя неизвестными. Затем находят
направляющий вектор
a
прямой L как векторное произведение нор-
мальных векторов плоскостей, задающих прямую L. Реализуем этот
98
подход на данном примере.
324110,
:
2310.
xyz
L
xyz
++−=
+−−=
Имеем
1
(3, 2, 4)
n = – нормальный вектор плоскости
324110,
xyz
++−=
2
(2, 1, 3)
n
=−
– нормальный вектор плоскости
2310.
xyz
+−−=
Тогда вектор
12
,
ann
=
является направляющим вектором пря-
мой L. Определим его координаты:
243432
3241017
132321
213
(10, 17, 1).
ijk
aijkijk
==⋅−⋅+⋅=−+−=
−−
−
=−−
Для нахождения точки
0000
(,,)
MxyzL
∈
зафиксируем одно из
координатных значений, например,
1.
x
=
Тогда, подставив в заданные
общие уравнения значение
1,
x
=
имеем:
248,
31
yz
yz
+=
−=−
или
2,
1,
y
z
=
=
т. е.
0
(1, 2, 1).
ML
∈
Таким образом, получаем искомые канонические уравнения за-
данной прямой L:
121
.
10171
xyz
−−−
==
−−
З а м е ч а н и е. Для нахождения точки
(
)
0000
,,
MxyzL
∈
можно
сначала решить систему в общем виде, а потом выбрать частное решение,
а в качестве
à
взять
[
]
12
,,
nn
α где
0,.
αα
≠∈
R
Пример 3. Доказать, что прямые L
1
и L
2
параллельны, и найти
расстояние между ними, если они заданы параметрическими уравне-
ниями:
1
21,
:3,
2
xt
Lyt
zt
=−+
=
=−
и
2
47,
:65,
24.
xt
Lyt
zt
=+
=−+
=−+
Решение. Прямая L
1
имеет направляющий вектор
1
(2, 3, 1),
a =− а
L
2
– вектор
2
(4, 6, 2),
a
=−−
причем
12
||,
aa
так как
2311
.
4622
−
===−
−−

99
Значит,
12
||.
LL
Найдем расстояние
12
(,)
dLL
между ними, используя формулу
расстояния (15.17) от точки до прямой. В параметрических уравнениях
заданных прямых полагаем
0,
t
=
имеем
11
(1, 0, 2),
ML
−∈
22
(7, 5, 4).
ML
∈ Тогда
122
1212
2
,
(,)(,).
MMa
dLLdML
a
==
Вычисляем векторное произведение:
122
,71504(2)656
462462
ijkijk
MMa
=−−−−==
−−−−
263656(26, 36, 56).
ijk=+−=−
После этого находим длины нужных векторов:
222
122
,2636(56)510821277;
MMa
=++−==
222
2
4(6)(2)1636456.
a =+−+−=++=
Значит,
12
5108212771277
(,).
14
56214
dLL ===
Пример 4. Доказать, что прямые L
1
и L
2
пересекаются, и найти ко-
ординаты точки пересечения, если они заданы параметрическими
уравнениями:
1
3,
:32,
1
xt
Lyt
z
=−
=+
=
и
2
51,
:131,
101.
xt
Lyt
zt
=+
=+
=+
Решение. Координаты направляющего вектора прямой равны со-
ответственно числовым коэффициентам при t, т. е.
11
(3, 3, 0)||,
aL
=−
22
(5, 13, 10)||.
aL
= При этом
12
||.
aa
/
Значит
12
||.
LL
/
Прежде всего определим, лежат ли прямые в одной плоскости,
т. е. являются ли векторы
1
,
a
2
a
и
12
MM
компланарными (здесь
11
(0, 2, 1),
ML
∈
22
(1, 1, 1)
ML
∈
). Найдем для этого их смешанное
произведение:
1212
330
(,,)513100.
110
aaMM
−
==
−
100
Значит, прямые лежат в одной плоскости и не параллельны. Сле-
довательно, они пересекаются.
Найдем точку их пересечения
0000
(,,).
Mxyz
Поскольку
01
,
ML
∈ то
0
1;
z
=
02
,
ML
∈ то
0
110.
zt
=+
Получаем, что при подстановке
0
1
z
=
в уравнение прямой
2
L
0.
t
=
Значит,
0
101,
x
=+=
0
101.
y
=+=
Итак,
0
(1, 1, 1)
M – точка пе-
ресечения заданных прямых.
Пример 5. Доказать, что прямые L
1
и L
2
скрещиваются, найти рас-
стояние между ними, если они заданы параметрическими уравнениями:
1
3,
:1,
22
xt
Lyt
zt
=+
=−+
=+
и
2
,
:32,
3.
xt
Lyt
zt
=−
=+
=
Решение. Направляющий вектор прямой L
1
есть
1
(1, 1, 2),
a =− а
прямой L
2
– вектор
2
(1, 3, 3),
a =− причем
12
||.
aa
/
Значит
12
||.
LL
/
Оп-
ределим, пересекаются ли прямые. Так как
11
(3, 1, 2),
ML
∈
22
(0, 2, 0),
ML
∈ то условием пересечения прямых служит компла-
нарность векторов
1
,
a
2
a
и
12
.
MM
Найдем смешанное произведение
этих векторов:
1212
112112
25
(,,)133025180.
24
312024
aaMM
−−
=−===≠
−
−−−
(15.19)
Значит, указанные векторы, а вместе с ними и прямые L
1
и L
2
, не
лежат в одной плоскости.
Прямые L
1
и L
2
скрещиваются, так как они не пересекаются и не
параллельны. Найдем расстояние между ними по формуле (15.18), ис-
пользуя (15.19):
12
12
18
(,).
,
dLL
aa
=
Определяем координаты:
12
121211
,112
331313
133
ijk
aaijk
−−
=−=⋅−⋅+⋅=
−−
−
952(9, 5, 2).
ijk=−−+=−−

101
Тогда
12
,81254110.
aa
=++=
Получаем:
12
18181109
(,)110.
11055
110
dLL ===
Задания
I уровень
1.1. Составьте параметрические уравнения прямой, прохо-
дящей через:
1) точку
0
(2, 0, 3)
M параллельно вектору
(3, 2, 2);
a
=−−
2) точку
0
(1, 2, 3)
M параллельно оси Oy;
3) точки
1
(1, 2, 1)
M
−
и
2
(2, 4, 0).
M
−
1.2. Определите, какие из точек
(2,1,5),
A
(0,4,3)
B и
(3,4,37)
C принадлежат прямой
2,
13,
52.
xt
yt
zt
=+
=+
=+
1.3. Определите по параметрическим уравнениям точку,
принадлежащую прямой, направляющий вектор и канонические
уравнения этой прямой:
1)
2,
12,
3;
xt
yt
zt
=+
=−
=
2)
5,
12,
5;
x
yt
zt
=
=−+
=+
3)
1,
3,
7.
xt
y
zt
=−+
=
=
1.4. Определите по каноническим уравнениям точку, при-
надлежащую прямой, направляющий вектор и параметрические
уравнения этой прямой:
1)
12
;
567
xyz
−+
==
−
2)
11
;
054
xyz
+−
== 3)
25
.
103
xyz
−+
==
II уровень
2.1. Составьте параметрические уравнения прямых:
102
1)
220,
10;
xyz
xyz
++−=
−+−=
2)
2470,
250.
xyz
xyz
++−=
+−−=
2.2. Составьте канонические уравнения следующих прямых:
1)
50,
23250;
xyz
xyz
++=
+−+=
2)
3220,
4320.
xyz
xyz
−+−=
+−−=
2.3. Составьте уравнения прямой, проходящей через точку
A(0, 1, – 4), параллельно прямой, заданной уравнениями:
210,
22360.
xyz
xyz
++−=
+−+=
2.4. Определите взаимное расположение прямых:
1)
2,
0,
2
xt
y
zt
=
=
=−
и
30,
10;
xyz
xyz
++−=
−+−=
2)
310,
30
xyz
xyz
+−+=
−++=
и
2510,
2390;
xyz
xyz
+−−=
−+−=
3)
23,
1,
4
xt
y
zt
=−+
=−
=−
и
220,
73170;
yz
xyz
−+=
−+−=
4)
10,
3130
xz
xyz
+−=
+−+=
и
230,
280.
xy
yz
−+=
+−=
III уровень
3.1. Дан треугольник с вершинами A(3, 7, 5), B(1, 2, 3) и
C(3, 0, 1). Составьте параметрические уравнения его медиан.
3.2. Дан треугольник с вершинами A(1, 2, – 7), B(2, 2, – 7) и
C(3, 4, – 5). Составьте параметрические уравнения его биссектрис.
3.3. Дан треугольник с вершинами A(1, – 2, – 4), B(3, 1, – 7) и
C(5, 1, – 7). Составьте канонические уравнения его высот.
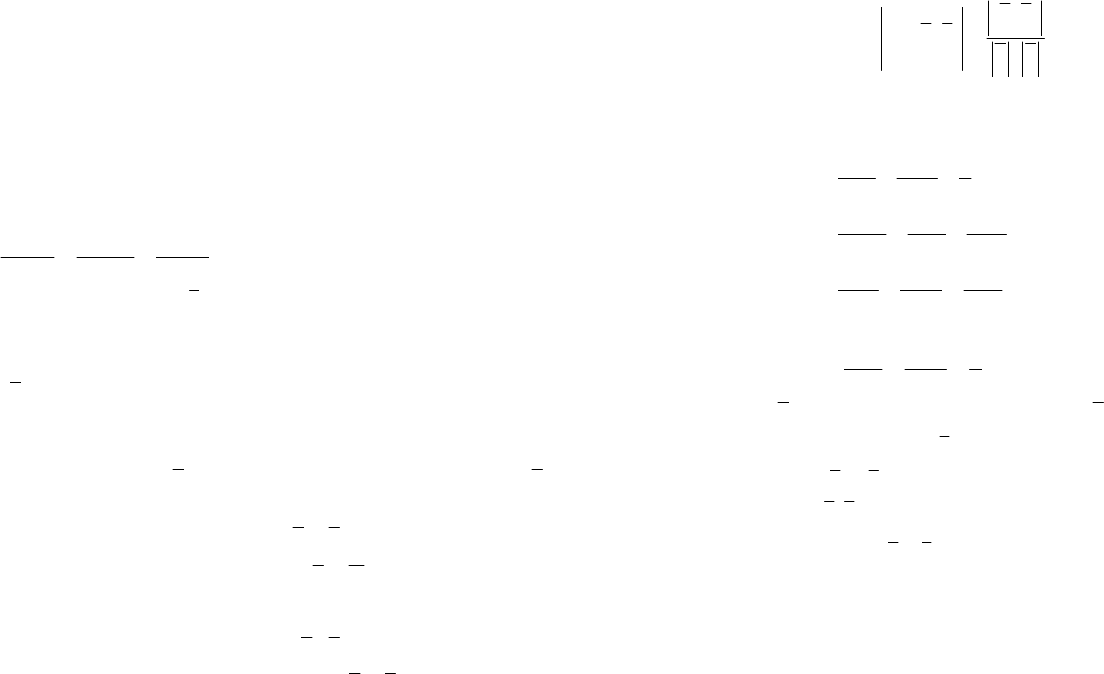
103
3.4. Составьте уравнения прямой, проходящей через точку
0
(0, 1, 4)
M
−
параллельно прямой
210,
22360.
xyz
xyz
++−=
+−+=
3.5. Докажите, что прямые скрещиваются, найдите расстоя-
ние между ними и угол, который они образуют:
1)
36,
14,
xt
yt
zt
=−
=−+
=
и
23,
4,
3;
xt
y
zt
=−+
=
=−
2)
210,
2340
xyz
xyz
+−+=
−+−=
и
90,
20.
xyz
xyz
++−=
−−=
15.3. Прямая и плоскость в пространстве
Пусть прямая L задана каноническими уравнениями:
000
:,
xxyyzz
L
klm
−−−
==
где
0000
(,,),
MxyzL
∈
(,,)||,
aklmL
= а плоскость P задана
общим уравнением:
:0,
PAxByCzD
+++=
где
(,,).
nABCP
=⊥
Тогда взаимное расположение прямой L и плоскости P в
пространстве можно определить по взаимному расположению
направляющего вектора
a
прямой L и нормального вектора
n
плоскости P. Справедливы утверждения:
||
LP
тогда и только тогда, когда
0
,;
anMP
⊥∉
LP
⊂
тогда и только тогда, когда
0
,
;
an
MP
⊥
∈
LP
⊥
тогда и только тогда, когда
||;
an
1
LPM
∩=
тогда и только тогда, когда
.
an
⊥/
104
В последнем случае координаты точки пересечения М
1
мо-
гут быть найдены следующим образом. От канонических урав-
нений прямой следует перейти к параметрическим, после чего
подставить x = x(t), y = y(t), z = z(t) в уравнение плоскости. Затем
надо разрешить полученное уравнение относительно параметра t
и найденное значение t подставить в параметрические уравнения
прямой. Это позволит найти значения x
1
, y
1
, z
1
, которые и будут
координатами искомой точки М
1
пересечения прямой L и плос-
кости P.
Углом ϕ между прямой и плоскостью называется угол ме-
жду прямой и ее ортогональной проекцией на плоскость, т. е.
(,)
sincos(,).
an
an
an
ϕ
∧
==
⋅
Пример 1. Установить взаимное расположение прямой и плоско-
сти. В случае их пересечения найти координаты точки пересечения:
1)
13
243
xyz
+−
==
и
33250;
xyz
−+−=
2)
1314
823
xyz
−−−
== и
2410;
xyz
+−+=
3)
745
514
xyz
−−−
== и
3250.
xyz
−+−=
Решение. 1) Определим координаты направляющего вектора пря-
мой
13
:
243
xyz
L
+−
==
по ее каноническим уравнениям. Это вектор
(2, 4, 3).
a = Нормальный вектор
n
плоскости
:33250
Pxyz
−+−=
имеет координаты
(3, 3, 2).
n =− Найдем скалярное произведение век-
торов
a
и
:
n
(
)
( )
,(2, 4, 3),(3, 3, 2)234(3)3261260.
an
=−=⋅+⋅−+⋅=−+=
Значит,
,
an
⊥
т. е. прямая L и плоскость P параллельны. Прове-
рим, не лежит ли прямая L в плоскости P. Для этого определим, при-
надлежит ли плоскости P точка
0
(1, 3, 0),
M − которая лежит на пря-
мой. Подставим ее координаты в уравнение плоскости:
3(1)33205395170.
⋅−−⋅+⋅−=−−−=−≠
Следовательно,
0
,
MP
∉
а значит,
||.
LP
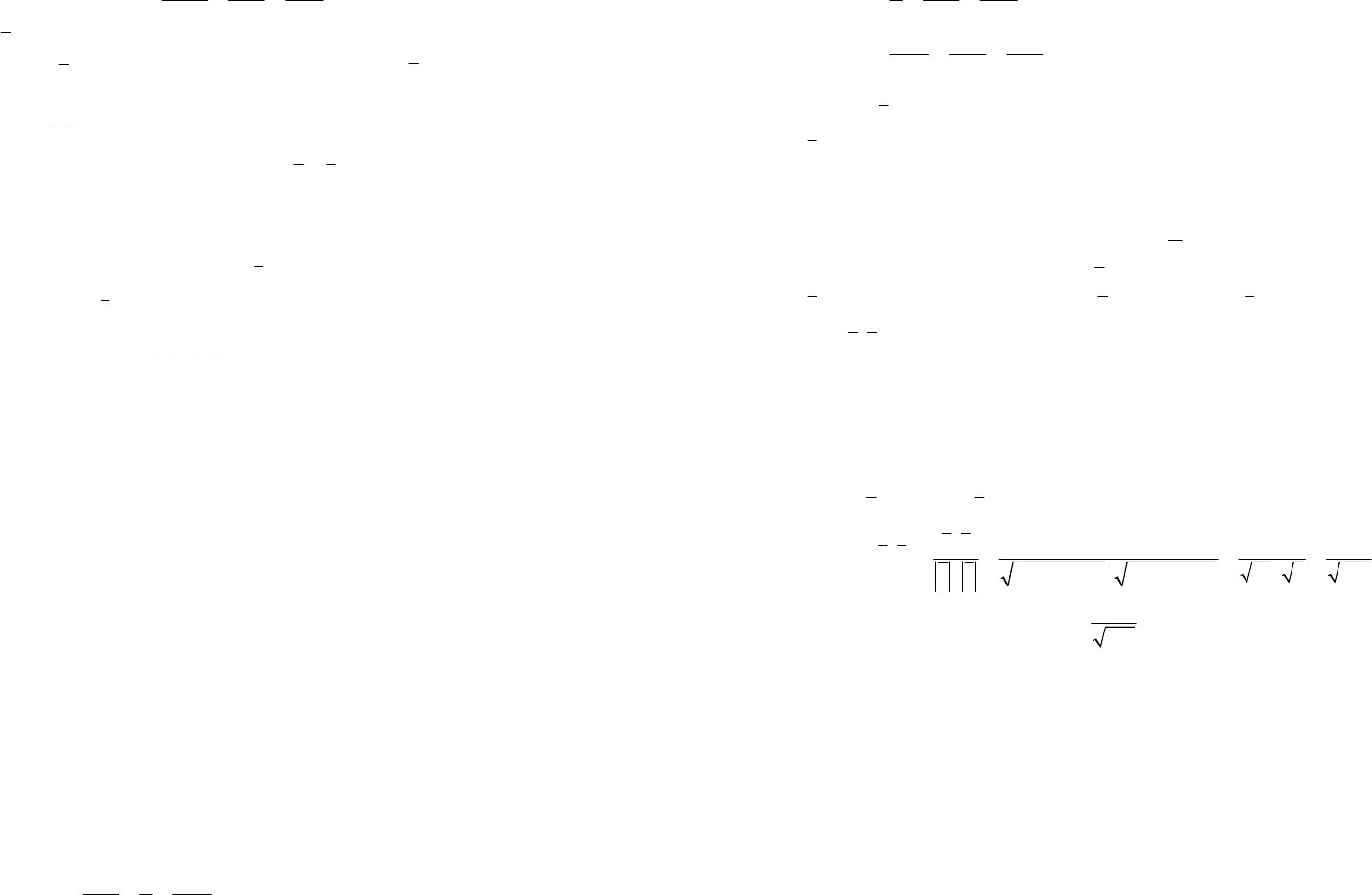
105
2) Прямая
1314
:
823
xyz
L
−−−
== имеет направляющий вектор
(8, 2, 3)
a = и проходит через точку
0
(13, 1, 4).
M Выясним, будет ли
вектор
a
перпендикулярен нормальному вектору
(1, 2, 4)
n
=−
задан-
ной плоскости
:2410.
Pxyz
+−+=
Вычислим скалярное произведение:
(
)
,81223(4)84120.
an
=⋅+⋅+⋅−=+−=
Поскольку оно равно нулю, то
.
an
⊥
Осталось проверить принадлежность точки
0
M
плоскости:
13214411321610.
+⋅−⋅+=+−+=
Значит, прямая L лежит в плоскости P.
3) Направляющий вектор
(5, 1, 4)
a= заданной прямой и нормаль-
ный вектор
(3, 1, 2)
n =− плоскости не коллинеарны и не перпендику-
лярны, так как
514
312
≠≠
−
(коэффициенты не пропорциональны) и
531(1)421518220
⋅+⋅−+⋅=−+=≠
(скалярное произведение не равно
нулю). Значит,
1
.
LPM
∩= Найдем координаты точки М
1
пересечения
прямой и плоскости. Для этого перейдем сначала к параметрическим
уравнениям прямой:
57,
4,
45.
xt
yt
zt
=+
=+
=+
Затем в уравнение плоскости P подставим вместо x, y, z их выра-
жение через параметр t:
3(57)(4)2(45)50,
ttt
+−+++−=
откуда имеем:
1521481050,
ttt
+−−++−=
т. е.
2222,
t
=−
1.
t
=−
Подставим найденное значение параметра t в параметрические
уравнения прямой:
75(1)752,
x
=+⋅−=−=
413,
y
=−=
54(1)541.
z
=+⋅−=−=
Получили точку
1
(2, 3, 1),
M в которой прямая пересекает плос-
кость.
Пример 2. Определить угол между прямой L и плоскостью P:
1)
12
:,:468110;
234
xyz
LPxyz
−+
==++−=
106
2)
13
:,:2350;
321
xyz
LPxy
+−
==−+=
3)
213
:,:230.
537
xyz
LPxy
+−−
==+−=
Решение. 1) По уравнению прямой L находим ее направляющий
вектор
(
)
2;3;4,
a = а для плоскости Р – нормальный вектор
(
)
4;6;8.
n =
Очевидно, что координаты этих векторов пропорциональны, а
значит, векторы являются коллинеарными. Следовательно, прямая L
перпендикулярна плоскости Р, т. е.
(,).
2
LP
π
∧
=
2) Направляющий вектор
a
прямой L имеет координаты
(
)
3;2;1,
a = а нормальный вектор
n
плоскости Р –
(
)
2;3;0.
n =− Так
как
(
)
( )
,3223100,
an
=⋅+⋅−+⋅=
то векторы перпендикулярны, а пря-
мая и плоскость параллельны. Определим, не лежит ли прямая L в
плоскости. Для этого координаты точки
(
)
0
0;1;3
ML
−∈
подставим в
уравнение плоскости:
(
)
203150.
⋅−⋅−+≠
Значит прямая и плоскость
параллельны, т. е.
(,)0.
LP
∧
=
3)
(
)
5;3;7,
a =
(
)
1;2;0.
n = Значит,
222222
(,)5132701111
cos(,).
835415
537120
an
an
an
∧
⋅+⋅+⋅
====
⋅
⋅
++⋅++
Таким образом
11
(,)arccos.
415
LP
∧
=
Пример 3. Найти координаты точки N, симметричной точке
(2, 5, 7)
M − относительно прямой, проходящей через точки
(5, 4, 6)
A и
(2, 17, 8).
B
−−−
Решение. 1-й способ. Построим плоскость Р, проходящую через
точку М перпендикулярно прямой АВ.
:7(2)21(5)14(7)0,
Pxyz
−−−+−−=
откуда Р:
3210.
xyz
++−=
Уравнения прямой АВ:
5,43,62.
xtytxt
=+=+=+
Найдем точку О пересечения плоскости Р и прямой АВ. Для этого
решим уравнение
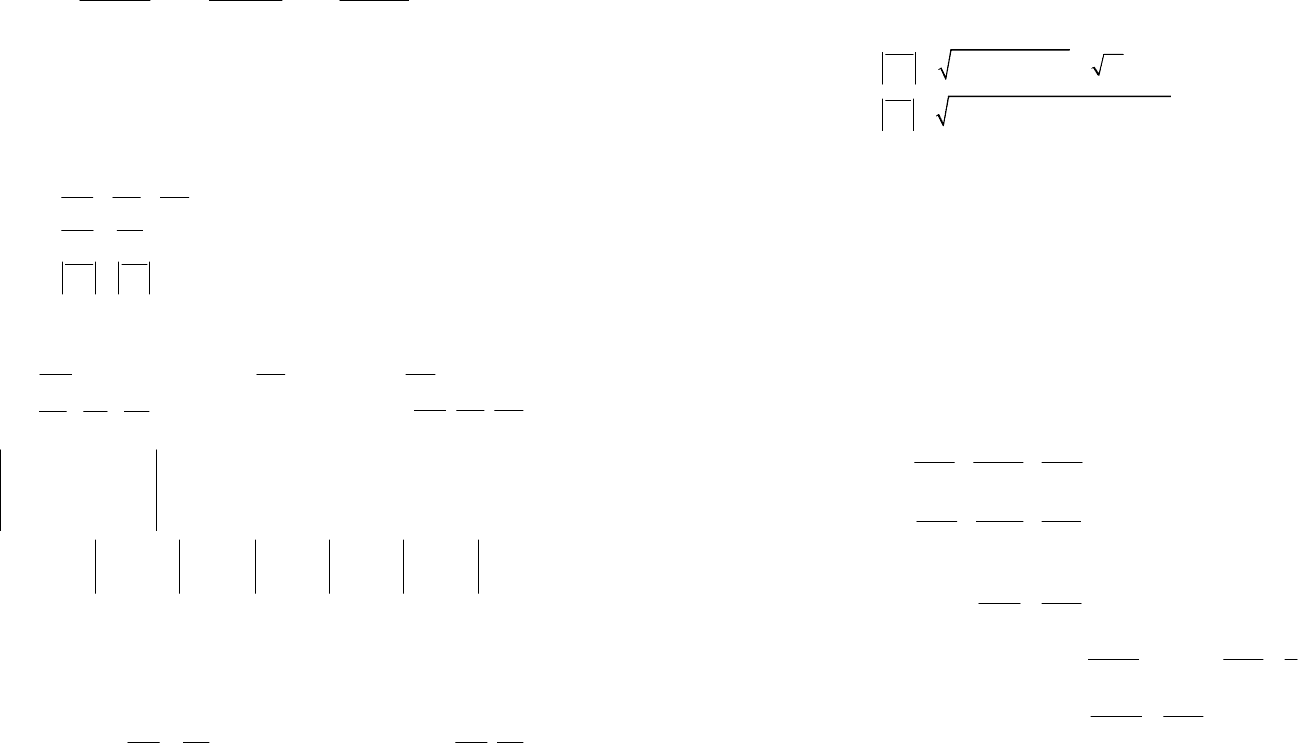
107
53(43)2(62)10,2.
tttt
+++++−==−
Значит, О(3, –2, 2). Так как
О – середина отрезка MN, то
000
,,.
222
MNMNMN
xxyyzz
xyz
+++
===
Зная координаты точек О и М, найдем N(4, 1, –3).
2-й способ. Для решения можно также воспользоваться следую-
щими рассуждениями: точка N, симметричная точке M, находится в
той же плоскости, что прямая AB и точка M, лежит на перпендикуляре
MN к прямой AB и удалена от прямой AB на то же расстояние, что и
точка M.
Пусть
(,,).
Nxyz
Тогда
1)
, ,
MNMAMB
– компланарны;
2)
;
MNAB
⊥
3)
;
MANA
=
4) середина отрезка MN лежит на прямой AB.
Составим систему уравнений, используя координатную форму за-
писи условий 1–3:
(2,5,7),
MNxyz
=−+−
(3, 9, 1),
MA
=−
(4, 12, 15).
MB =−−−
, ,
MNMAMB
компланарны при условии
(
)
,,0,
MNMAMB
=
т. е.
257
3910,
41215
xyz−+−
−=
−−−
откуда получаем:
913139
(2)(5)(7)0,
1215415412
xyz
−−
−−++−=
−−−−−−
147(2)49(5)0(7)0,
xyz
−−+++−=
т. е.
147495390.
xy
−++=
После сокращения имеем:
3110,
xy
−−=
откуда
311.
yx
=−
(15.20)
Условие
MNAB
⊥ равносильно условию
(,)0
MNAB
=
или
(2)(25)(5)(174)(7)(86)0,
xyz
−−−++−−+−−−=
что приводит к
уравнению
7(2)21(5)14(7)0.
xyz
−−−+−−=
После преобразования имеем:
3210.
xyz
++−=
108
Далее получим:
213(311)1034,
zxxx=−−−=−+
откуда
517.
zx
=−+
(15.21)
Вычислим:
222
39(1)91;
MA =++−=
222
(5)(4)(6).
NAxyz
=−+−+−
Равенство этих величин дает нам:
222
(5)(4)(6)91.
xyz−+−+−=
Подставим в последнее равенство правые части формул (15.20) и
(15.21) вместо y и z соответственно, откуда получим уравнение
2
680.
xx
−+=
Решим это уравнение, найдя корни
1
2,
x
=
2
4.
x
=
Соответствующие значения y, z вычислим, используя равенства
(15.20) и (15.21). Получим точки
1
(2, 5, 7)
N − и
2
(4, 1, 3),
N
−
кото-
рые удовлетворяют первым трем условиям. Осталось проверить чет-
вертое условие. Найдем середины О
1
и О
2
отрезков
1
MN
и
2
MN
соот-
ветственно:
1
225577
, ,
222
O
+−−+
или
1
(2, 5, 7);
O −
2
245173
, ,
222
O
+−+−
или
2
(3, 2, 2).
O −
Проверим, какая из точек (О
1
или О
2
) лежит на прямой АВ:
46
:5.
32
yz
ABx
−−
−==
1
,
OAB
∉ так как
54
253,
3
−−
−==−
но
761
3;
22
−
=≠−
2
,
OAB
∈ так как
2426
352.
32
−−−
−===−
Приходим к ответу:
(4, 1, 3).
N
−
Пример 4. Прямая L задана как линия пересечения плоскостей
0,
220.
xyz
xy
+−=
−+=
Написать уравнение ее проекции на координатную плоскость Oxz.
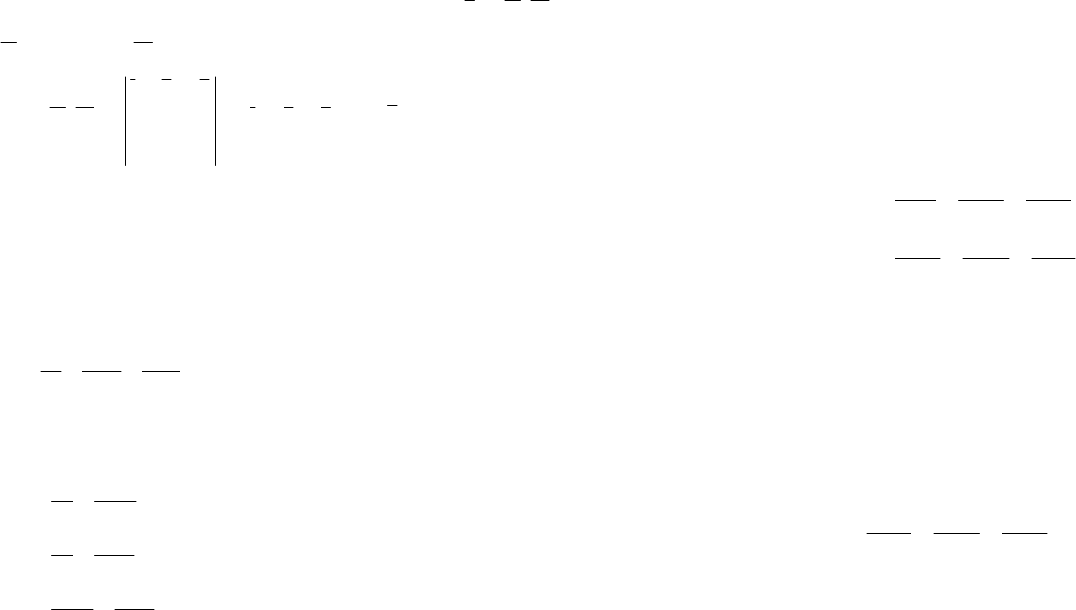
109
Решение. Построим канонические уравнения прямой L. В качест-
ве направляющего вектора можно взять вектор
12
,,
ann
=
где
1
(1, 1, 1),
n
=−
2
(2, 1, 0).
n=− Тогда
12
,11123,
210
ijk
nnijk
=−=−−−
−
т. е.
(1, 2, 3).
a
=−−−
Если
0,
x
=
то получим систему уравнений
0,
20,
yz
y
−=
−+=
из которой найдем
2,
y
=
2,
z
=
а значит точка
0
(0, 2, 2)
M лежит на
прямой L.
Таким образом, канонические уравнения прямой L таковы:
22
,
123
xyz
−−
==
−−−
что эквивалентно системе трех уравнений, описывающих три плоско-
сти, проектирующие прямую на координатные плоскости Oxy, Oxz и
Oyz соответственно:
2
,
12
2
,
13
22
.
23
xy
xz
yz
−
=
−−
−
=
−−
−−
=
−−
После упрощения получаем:
220,
320,
3220.
xy
xz
yz
−+=
−+=
−−=
Искомое уравнение:
320.
xz
−+=
Задания
I уровень
1.1. Найдите точку пересечения прямой
L
с плоскостью
P
или установите их параллельность:
110
1)
24,
:1,
2,
xt
Lyt
zt
=+
=−+
=−
:4130;
Pxyz
+−+=
2)
23,
:1,
2,
xt
Lyt
zt
=−
=−+
=−
:30;
Pxyz
+−+=
3)
132
:,
215
xyz
L
−++
==
−
:4330;
Pxyz
+−+=
4)
745
:,
514
xyz
L
−−−
==
:3250;
Pxyz
−+−=
5)
2340,
:
2220,
xyz
L
xyz
−++=
−−+=
:4580.
Pxyz
−−+=
1.2. Найдите угол между прямой и плоскостью:
1)
111,
27,
58
xt
yt
zt
=+
=−
=−
и
782100;
xyz
−+−=
2)
362
214
xyz
−−+
==
−
и ;0523
=
−
+
−
zyx
3)
4270,
3720
xyz
xyz
+−+=
+−=
и
310.
xyz
+−+=
1.3. Составьте уравнение плоскости, проходящей через на-
чало координат и прямую
13,
24,
52.
xt
yt
zt
=+
=+
=−
II уровень
2.1. Определите, при каком значении m прямая
13,
2,
32
xt
ymt
zt
=−+
=+
=−−
не имеет с плоскостью
3320
xyz
++−=
общих точек.

111
2.2. Найдите, при каких значениях m и n прямая
213
322
xyz
−+−
==
−
лежит в плоскости
20.
mxyzn
+−+=
2.3. Найдите, при каких значениях m и n прямая
3230,
43410
xyz
xyz
−++=
−++=
перпендикулярна плоскости
820.
mxynz
+++=
2.4. Составьте уравнение плоскости, проходящей через пря-
мую
3240,
2310
xyz
xyz
+−−=
−+−=
параллельно прямой
32,
61,
4.
xt
yt
zt
=+
=−
=
2.5. Составьте уравнение плоскости, проходящей через
ось Oz параллельно прямой
2,
2,
31.
xt
yt
zt
=+
=
=+
2.6. Составьте уравнение прямой, проходящей через точку
(1, 2, 1)
A и перпендикулярной плоскости
37250.
xyz
+−+=
2.7. Найдите проекцию точки
(2, 11, 5)
A
−
на плоскость
4270.
xyz
+−+=
2.8. Найдите точку, симметричную точке
(6, 5, 5)
A
−
отно-
сительно плоскости
2340.
xyz
−+−=
2.9. Напишите уравнение плоскости, проходящей через точ-
ку
(1, 2, 2)
A
−
перпендикулярно прямой
363
.
432
xyz
+−−
==
−
2.10. Составьте уравнение плоскости, проходящей через
прямую
2350,
32210
xyz
xyz
+−+=
−+−=
параллельно вектору
(1, 1, 1).
a =
112
III уровень
3.1. Составьте параметрические уравнения прямой, которая
проходит через точку
(3, 2, 4)
A
−−
параллельно плоскости
32370
xyz
−−−=
и пересекает прямую
23,
42,
12.
xt
yt
zt
=+
=−−
=+
3.2. Найдите проекцию прямой L на плоскость
32150,
xyz
−−+=
если она задана уравнениями:
1)
12,
3,
2;
xt
yt
xt
=+
=+
=+
2)
50,
2340.
xyz
xyz
++−=
−+−=
3.3. Найдите основание перпендикуляра, проведенного из
точки
(1, 2, 3)
A к прямой
83,
1,
62.
xt
yt
zt
=+
=+
=−
3.4. Найдите точку, симметричную точке
(3, 1, 1)
A
−−
от-
носительно прямой
43130,
250.
xy
yz
−−=
−+=
3.5. Составьте уравнение плоскости, перпендикулярной
плоскости
5320
xyz
−+−=
и:
1) пересекающей ее по прямой, лежащей в плоскости Oxy;
2) проходящей через прямую
2350,
220.
xyz
xyz
−+−=
+−+=
3.6. Составьте уравнение прямой, проходящей через точку
пересечения плоскости
10
xyz
++−=
с прямой
,
1,
1,
xt
y
z
=
=
=−
при
условии, что искомая прямая принадлежит заданной плоскости и
перпендикулярна заданной прямой.

113
15.4. Поверхности второго порядка
Поверхностью второго порядка называется поверхность S,
общее уравнение которой в декартовой прямоугольной системе
координат имеет вид:
222
2222220,
AxByCzDxyExzFyzGxHyKzL
+++++++++=
(15.22)
где коэффициенты при одночленах второй степени одно-
временно не равны нулю.
Существует девять типов невырожденных поверхностей,
уравнения которых с помощью преобразования координат могут
быть приведены к одному из следующих видов. Эти уравнения
определяют тип поверхности и называются каноническими
уравнениями.
1. Эллипсоид:
222
222
1
xyz
abc
++=
(рис. 15.1).
Рис. 15.1
2. Конус второго порядка:
222
222
0
xyz
abc
+−=
(рис. 15.2).
Рис. 15.2
114
3. Гиперболоиды
1) однополостный:
222
222
1
xyz
abc
+−=
(рис. 15.3);
2) двуполостный:
222
222
1
xyz
abc
+−=−
(рис. 15.4).
Рис. 15.3 Рис. 15.4
4. Параболоиды
1) эллиптический:
22
22
2
xy
z
ab
+=
(рис. 15.5);
2) гиперболический:
22
22
2
xy
z
ab
−=
(рис.15.6).
Рис. 15.5 Рис. 15.6
5. Цилиндры
1) эллиптический: 2) гиперболический:
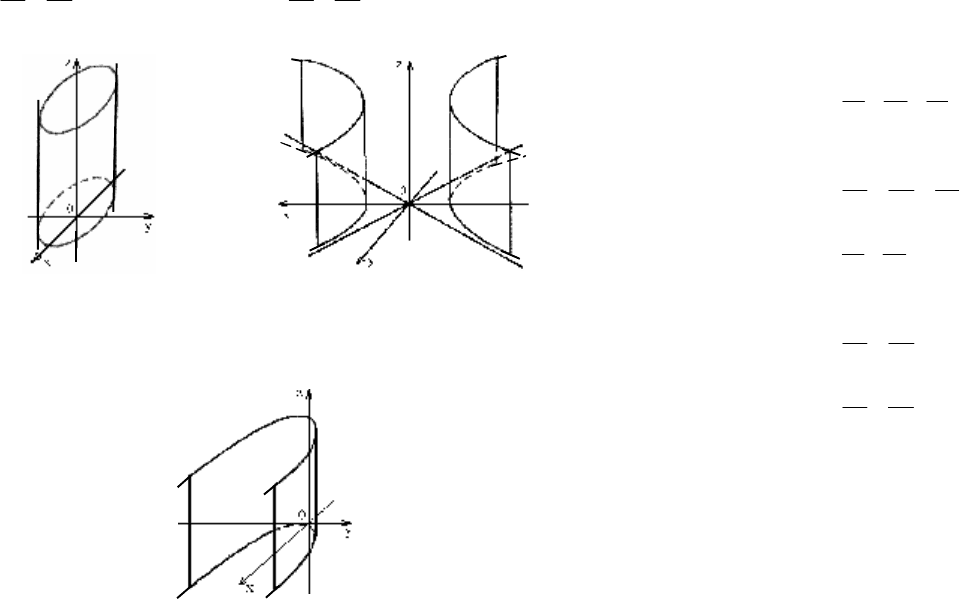
115
22
22
1
xy
ab
+=
(рис. 15.7);
22
22
1
xy
ab
−=
(рис. 15.8);
Рис. 15.7 Рис. 15.8
3) параболический:
2
2 (0)
ypxp
=>
(рис. 15.9).
Рис. 15.9
Основным методом исследования формы поверхности явля-
ется метод параллельных сечений, который состоит в следую-
щем. Поверхность пересекается координатными плоскостями и
им параллельными, а затем на основании вида полученных в се-
чениях линий делается вывод о типе поверхности. Таким обра-
зом можно изучать основные геометрические свойства невыро-
жденных поверхностей второго порядка на основе их канониче-
ских уравнений.
При этом, когда в общем уравнении поверхности коэффици-
енты
0,
DEF
===
приведение к каноническому виду осущест-
вляется с помощью метода выделения полных квадратов.
116
В определенных случаях уравнение (15.22) поверхности
может быть приведено к уравнениям, задающим, так называе-
мые, вырожденные поверхности. Приведем примеры таких
случаев:
222
222
1
xyz
abc
++=−
– пустое множество точек (мнимый эллип-
соид);
222
222
0
xyz
abc
++=
– точка (0, 0, 0);
22
22
1
xy
ab
+=−
– пустое множество точек (мнимый эллиптиче-
ский цилиндр);
22
22
0
xy
ab
+=
– прямая (ось Oz);
22
22
0
xy
ab
−=
– пара пересекающихся плоскостей;
22
(0)
xaa
=≠
– пара параллельных плоскостей;
22
(0)
xaa
=−≠
– пустое множество точек;
2
0
x
=
– плоскость (пара совпадающих плоскостей).
Пример 1. Привести уравнение к каноническому виду и опреде-
лить тип поверхности, которую оно задает:
1)
222
488164320;
xyzxyz
+−+−+−=
2)
22
3262410;
xzxyz
−++++=
3)
222
236412130;
xyzxyz
++−+−−=
4)
22
4916902050.
xyxy
++−+=
Решение. 1) Воспользуемся методом выделения полных квадратов.
Преобразуем левую часть уравнения:
222
48816432
xyzxyz
+−+−+−=
222
4(211)8(211)(444)32
xxyyzz
=++−+−+−−−+−−=
222
4(1)48(1)8(2)432
xyz
=+−+−−−−+−=
222
4(1)8(1)(2)40.
xyz=++−−−−
Значит, заданное уравнение равносильно уравнению
