Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.

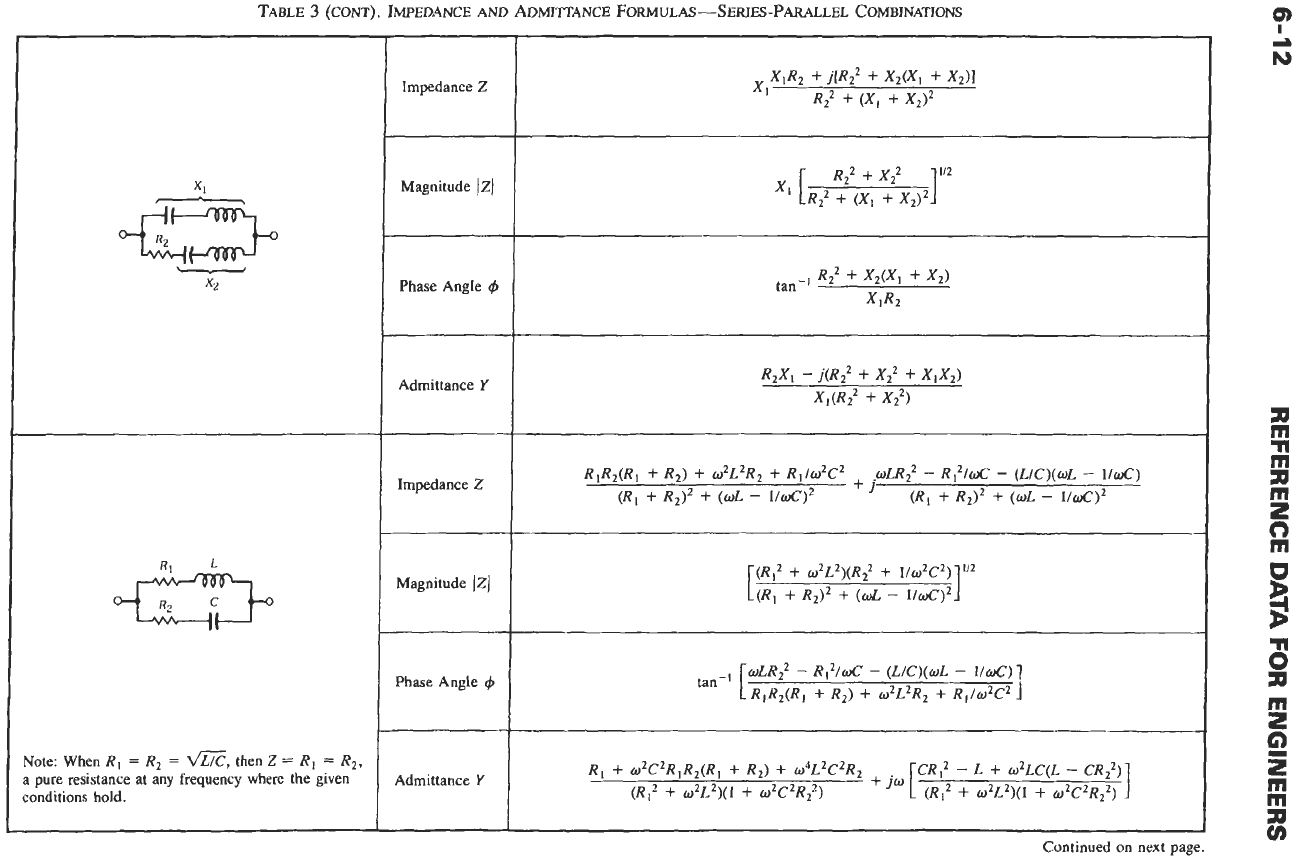
TABLE
3
(CONT).
IMPEDANCE
AND
ADMITTANCE
FORMULAS-SERESPARALLEL
COMBINATIONS
rlote: When
RI
=
R2
=
m,
then
Z
=
R,
=
R2,
I
pure
resistance
at
any frequency where
the
given
:onditions hold.
Impedance
Z
Magnitude
lZl
Phase Angle
q5
Admittance
Y
Impedance
2
Magnitude
lZl
Phase
Angle
c$
Admittance
Y
RIR2(Rl
+
R2)
+
02LZR2
+
RI/o2C2
oLR~
-
R1210C
-
(LIC)(oL
-
lld)
+
R,)Z
+
(wL
-
+
j
(RI
+
R2)2
+
(d
-
l/oC)2
(RI2
+
02L2)(R2
+
l/02C2)
(R,
+
R2)2
+
(wL
-
l/ft~C)~
1
I
dR2’
-
RI2/WC
-
(L/C)(wl,
-
I/&)
+
Rz)
+
02L2R2
+
RI/02C2
R,
+
02C2RlR2(Rl
+
R2)
+
w4L2C2R2
+jo
I2
-
L
+
w2LC(L
-
CR?)
(RI2
-F
w2L2)(1
+
wZCZR?)
[:;
+
ozL2)(1
+
02C2R$)
1
Continued on next
page.

TABLE
3
(CONT)
.
IMPEDANCE AND
ADMITTANCE
FORMULAS-SERIES-PARALLEL
COMBINATIONS
Impedance
Z
Magnitude
IZI
Phase
Angle
4
Admittance
Y
Z=R+jX

6-14
REFERENCE
DATA
FOR ENGINEERS
50
40
2
5
e“
0
a
u
30
0
c
K
20
m
2
Y
10
SCALE C
0
40
80
120
160
ZOO
240
1
00-5
0
2
4
6
8
10
SCALEA
0
10
20
30 40
50
SCALEB
DYJ
FOR COPPER AT 20’C. OR
D,Tv*
FOR ANY CONDUCTOR MATERIAL
Fig. 7. Resistance ratio for isolated straight solid conductors
of circular cross section.
Eqs. (2) and (3) hold for isolated straight conductors of
any
shape.
In
this case the term
D
=
(perimeter of cross
section)/.rr.
Examples:
(A)
At
100
megahertz, a copper conductor has a
depth of penetration
TI
=
0.00035
inch.
(B)
A
steel shield with 0.005-inch copper plate,
which is practically equivalent in
R,,
to an isolated
copper conductor 0.005-inch thick, has a value of
A
=
1.23 at 200 kilohertz. This 23-percent increase in
resistance over that of a thick copper sheet is satisfactor-
ily
low as regards its effect on the losses of the
components within the shi1e.d
By
comparison, a thick
aluminum sheet has a resistance
(p/pC)”’
=
1.28 times
that of copper.
EQUATIONS
FOR
SIMPLE
R,
L,
AND
C
NETWORKS*
Self-Inductance of Circular
Ring of Round Wire at Radio
Frequencies, for Nonmagnetic
Materials
L
=
(d100)
X
[7.353 logIo(l6ald)
-
6.3861
*
Many equations for computing capacitance, inductance,
and mutual inductance will be found in Bureau of Standards
Circular
No.
C74, obtainable from the Superintendent of
Documents, Government Printing Office, Washington, D.C.
20402.
TABLE
4.
SKIN-EFFECT CORRECTION
TUBULAR CONDUCTORS
COEFFICIENT
A
FOR
SOLID
AND
Solid Conductors
W”2)[~L,(~c~~)l
‘I2
A
>
370 1
.ooo
220
1.005
160 1.010
98 1.02
48 1.05
26
1.10
13 1.20
9.6 1.30
5.3 2.00
<
3.0
i=
Rdc
RdC
(lO.37/~*)(p/pc)
X
ohm/foot
Tubular Conductors
T(f’!2)[PL,(P,/P)l
’/*
A
Rac/Rdc
=
B where B
>
3.5 1
.oo
0.384B
3.5 1
.oo
1.35
3.15 1.01 1.23
2.85 1.05 1.15
2.60
1.10
1.10
2.29 1.20 1.06
2.08
1.30 1.04
1.77
1
SO
1.02
1.31 2.00 1
.oo
=
B where
B
<
1.3 2.60IB
1
.oo
where,
L
=
self-inductance in microhenrys,
a
=
mean radius of ring in inches,
d
=
diameter of wire in inches,
a/d
>
2.5.
Capacitance
For Parallel-Plate Capacitor:
C
=
O.O8856,[(N
-
l)A]/t
=
0.225e,[(N
-
l)A”/t”]
where,
C
=
capacitance in picofarads,
A
=
area
of
one side of one plate in square
centimeters,
A”
=
area in square inches,
N
=
number of plates,
t”
=
thickness in inches,
E,
=
dielectric constant relative to air.
t
=
thickness
of
dielectric
in
centimeters,

FUNDAMENTALS OF NETWORKS
6-15
This equation neglects “fringing” at the edges of the
plates.
For Coaxial Cylindrical Capacitor (Fig.
8):
c
=
2r€,E”/[log,(b/U)1
=
((5
x
lo6~,)i[c2~og,(b/a)]}
where,
C
=
capacitance per unit axial length in
c
=
velocity
of
light in vacuo, meters per second
E,
=
dielectric constant relative to air,
E,
=
permittivity of free space in faraddmeter
faraddmeter,
=
2.998
X
lo8,
=
8.85
X
lo-”
Alternative forms of the equation are:
C
=
0.2416~,/[log
lo(b/u)]
picofarads/centimeter
=
0.6 14~,/[log lo(b/a)] picofaraddinch
=
7.3
6.5, /[log (Ma)] picofarads/foot
When
1.0
<
(Ha)
<
1.4, then with accuracy
of
1
percent or better, the capacitance in picofarads/foot is:
(Ha)
+
1
C
=
8.506,
~
(blu)
-
1
T-7~
or Y-A Transformation
The two networks (Fig.
9)
are equivalent, as far as
conditions at the terminals are concerned, provided the
listed equations are satisfied (either the impedance
equations or the admittance equations may be used)
Y1
=
l/Zl
Y,
=
UZ,, etc.
TRANSIENTS-ELEMENTARY
CASES
The complete transient in a linear network is, by the
principle
of
superposition, the sum
of
the individual
transients due to the store
of
energy in each inductor
and capacitor and to each external source
of
energy
connected to the network. To this is added the steady-
state condition due to each external source
of
energy.
The transient may be computed as starting from any
arbitrary time t
=
0
when the initial conditions of the
energy of the network are known.
Time Constant
The time constant (designated
T)
of
the discharge
of
a capacitor through a resistor is the time
t2
-
tl
required
for the voltage or current to decay to 1/~
of
its value at
time
tl.
For the charge of a capacitor, the same
definition applies, the voltage “decaying’’ toward its
steady-state value. The time constant of discharge or
charge
of
the current in an inductor through a resistor
follows an analogous definition.
Stored energy, in joules (watt-seconds), is:
Energy stored in a capacitor
=
CE2/2
Energy stored in an inductor
=
L12/2
In the equations in this section,
T
and
t
are in seconds,
R is in ohms,
L
is in henrys,
C
is
in farads, E is in volts,
and
I
is in amperes. Values
of
the numerical constants
are:
E
=
2.718
1/~
=
0.3679
lOgloE
=
0.4343
Capacitor Charge and
Discharge
Closing of switch (Fig. 10) occurs at time
t
=
0.
Initial conditions (at
t
=
0):
Battery
=
E,;
e,
=
Eo.
Steady state (at
t
=
x):
i
=
0;
e,
=
Eb.
Transient:
i
=
[(Eb
-
E,)/R]exp(-t/RC)
=
Io
exp(-t/RC)
loglo(i/lo)
=
-(0.4343/RC)t
e,
=
Eo
+
C-’
i dt
=
Eo
exp(-t/RC)
+
Eb[1
-
exp(-t/RC)]
Time constant:
T
=
RC
Fig.
11
shows current:
i/lo
=
exp(-t/T)
Fig.
11
shows discharge (for Eb
=
0):
e,/Eo
=
exp(-t/T)
Fig. 12 shows charge (for Eo
=
0):
e,/Eb
=
1
-
eXp(-t/T)
These curves are plotted for a wider range in Fig. 13.
Fig.
8.
Coaxial cylindrical capacitor.

6-16
REFERENCE
DATA
FOR ENGINEERS
(A)
Tor
Y
Fig.
9.
T
or
Y
network and
n
or
A
network.
Two
Capacitors
Closing
of
switch (Fig.
14)
occurs at time
t
=
0.
Initial conditions (at
t
=
0):
e,
=
El;
Steady state (at
t=m):
e2
=
E2
el
=
Efi
e2
=
-Ej;
i
=
0
Ej
=
(EICI
-
E~CZ)/(CI
+
C2)
C‘
=
C,C,/(CI
+
C,)
Transient:
i
=
[(E,
+
E2)/R]
exp(-tlRC’)
e,
=
Ej
+
(E,
-
Ej)
exp(-t/RC‘)
=
E,
-
(E1
+
E~)(C’/CI)
x
[1
-
exp(-t/RC’)I
e2
=
-Ej
+
(E2
+
Ef)
exp(-t/RC’)
(6)
li
or
A.
=
E2
-
(El
+
EZ)(C‘/C,)
x
[l
-
exp( -t/RC’)]
Original energy (joules)
=
(c~E,’
+
~2~,2)/2
Final energy (joules)
=
(C,
+
C2)E,2/2
~oss
of
energy (joules)
=
i2R
dt
=
C’
(E,
+
E,)2/2
(Loss
is independent
of
the value
of
R.)
Inductor Charge and Discharge
Initial conditions (at
t
=
0)
in
Fig.
15:
Battery
=
E,;
i
=
I,
Steady state (at
t
=
30):
i
=
Ij
=
EbIR
Fig.
10.
Circuit for capacitor charge and discharge.
Fig.
11,
Capacitor discharge.

FUNDAMENTALS
OF
NETWORKS
6-1
7
0 1.0 2.0
t/r
Fig.
12.
Capacitor charge.
Transient plus steady state:
i
=
lf[l
-
exp(-RtlL)]
+
lo
exp(-RtlL)
eL
=
-L dildt
=
-(Eb
-
Rl,) exp(-RflL)
Time constant:
T
=
LIR
Fig. 11 shows discharge (for Eb
=
0):
illo
=
exp(-tlT)
Fig. 12 shows charge (for
lo
=
0)
illf
=
[l
-
exp(-tlT)]
These curves
are
plotted for a wider range in Fig. 13.
Charge
and
Discharge
of
Series
R-L-C Circuit
Initial conditions (at
t
=
0)
in
Fig. 16:
Battery
=
Eb;
e,
=
Eo;
i
=
lo
Use exponential exp(
-
t/T)
for
charge
or
discharge
of
capacitor
or
discharge
of
(current at time r)/(initial current)
2
2
VI
inductor:
z
z
Discharge
of
capacitor:
e
(voltage at time t)/(initial voltage)
5
B
w
Use exponential
1
-
exp(
-
r/T)
VI
3
for
charge
of
capacitor:
(voltage at time t)/(battery or final voltage)
Charge
of
inductor:
II
c
(current at time r)/(final current)
Steady state (at
t
=
00):
i
=
0;
e,
=E,
Differential equation:
i dt
-
Ri
-
L(di1dt)
=
0
when
L(d’i1dt’)
+
R(di/dt)
+
(i/C)
=
0
Solution of equation:
[2(Eb
-
Eo)
-
Rzo
sinh (RtI2L)
i
=
exp(-Rt/2L)
R(D~/~)
1
X
(D1”)
+
lo
cosh (Rt/2L)(D”*)
where D
=
1
-
(4L/R2C).
Case 1: When LIR2C is small
i
=
(1
-
7-4
-
2A2)-’
[
[Eb
~
Eo
-
Zo(A
+
A’)]
xexp(-L(l
+A+2A2))
RC
lo(1
-
A
-
A’)
-
E
R
-“I
x
exp
(-E
(1
-
A
-
A’))]
L
where
A
=
LlR2C.
For
practical purposes, the terms
A’
can be neglected
when
A
<
0.1. The terms
A
may be neglected when
A
<
0.01.
EXPONENTIAL
f
-r/T
0
010 0
020
0
030
0
0500
070
0
100
0
20
0
30
0
50
0
70
1
0
0
1
2
3
4
5
099
098
097 095
093
090
080
070 050 030000
EXPONENTIAL
1
-
c
Fig.
13.
Exponential functions exp(-tlT) and
1
-
exp(-r/T) applied to transients in
R-C
and
L-R
circuits.

6-18
I
REFERENCE
Fig.
14.
Circuit for
two
capacitors.
Case 2: When 4L/R2C
<
1
for which
0"'
is real
Case
3:
When
D
is a small positive or negative
quantity
This equation may be used for values of
D
up to 20.25,
at which values the error in the computed current
i
is
approximately 1 percent of
Io
or of (Eb
-
Eo)/R.
Case
3A:
When 4L/R2C
=
1
for which
D
=
0,
the
equation reduces to
i
=
exp(-Rt/2L) [Eb
~
;
Eo
'L'
-
+
Io
(1
-
E)]
or
i
=
il
+
i,,
plotted in Fig. 17. For practical
purposes, this equation may be used when 4LIR2C
=
1
2
0.05
with errors of
1
percent or less.
Case 4: When 4L/R2C
>
1
for which
D'/2
is
imaginary
DATA
FOR ENGINEERS
Fig.
15.
Circuit for inductor charge and discharge
i
=
exp(-Rt/2L
___
-
-
::L)
=
I,
exp (-Rt/2L) sin
(mot
+
V)
where,
"
"1
=
tan-'{woLIo/[Eb
-
EO
-
RZ&2]}
The envelope of the voltage wave across the inductor
is
?exp( -R~/~L)[w~(LC)~/~]
-I
X
{[Eb
-
Eo
-
(RZO)/2l2
+
w~L~Z~}~'~
Example:
Relay with transient-suppressing capacitor
(Fig. 18). The switch is closed until time
t
=
0,
then
opened.
Let L
=
0.10
henry, Rl
=
100
ohms, and
E
=
10
volts.
Suppose we choose
C
=
farad and R,
=
100
ohms.
Then R
=
200 ohms,
Io
=
0.10
ampere,
Eo
=
10
volts,
o0
=
3
X
IO3,
and&
=
480 hertz.
Maximum peak voltage across L (envelope at
t
=
0)
is approximately
30
volts. Time constant of decay of
envelope
is
0.001 second.
Nonoscillating Condition: It is preferable that the
circuit be just nonoscillating (Case
3A)
and that it
present a pure resistance at the switch terminals for any
frequency.
10
05
0
-0
5
012345
RtI2L
Fig.
16.
Series
R-L-C circuit.
Fig.
17.
Transients
for
4LIR2C
=
1.

FUNDAMENTALS
OF
NETWORKS
6-19
Fig.
18.
Equivalent circuit
of
relay with transient-suppressing
capacitor.
R,
=
R,
=
R/2
=
100 ohms
4L/R2C
=
1
C
=
farad
=
10 microfarads
e
(AI
Actual clrcult.
J-?
At the instant of opening the switch, the voltage across
the parallel circuit is
E,
-
R2Zo
=
0.
Series R-L-C Circuit
With
Sinusoidal Applied Voltage
By the principle
of
superposition, the transient and
steady-state conditions are the same for the actual
circuit and the equivalent circuit shown in Fig. 19, the
closing of the switch occurring at time
t
=
0.
In the
equivalent circuit, the steady state is due to the source
e
acting continuously from time
t
=
--m,
while the
transient is due to short-circuiting the source
-e
at time
t
=
0.
Source:
e
=
E
sin(ot
+
a)
Steady state:
i
=
(E/Z)
sin(wt
+
a
-
4)
where,
2
=
{R2
+
[wL
-
(1/wC)]2}”2
tan4
=
(w2LC
-
l)/OCR
The transient is found by determining current
i
=
Io
and
capacitor voltage
e,
=
EO
at time
t
=
0,
due to the
source
-e.
These values of
I,
and
E,
are
then substitut-
ed in the equations of Case
1,
2,
3,
or
4,
above,
according to the values of R, L, and
C.
At time
t
=
0,
due to the source
-e:
i
=
I,
=
-(E/Z)
sin(a
-
4)
e,
=
Eo
=
(E/oCZ)
cos(a
-
4)
This form of analysis may be used for any periodic
applied voltage
e.
The steady-state current and the
(BJ
Equlualent clrcult
Fig.
19.
Series
R-L-C
circuit.
capacitor voltage for an applied voltage
-e
are
deter-
mined, the periodic voltage being resolved into its
harmonic components for this purpose, if necessary.
Then the instantaneous values
i
=
Io
and
e,
=
E,
at the
time of closing the switch are easily found, from which
the transient is determined. It is evident, from this
method
of
analysis, that the waveform of the transient
need bear no relationship to that of the applied voltage,
depending only on the constants of the circuit and the
hypothetical initial conditions
I,
and
E,.
TRANSIENTS-OPERATIONAL
CALCULUS AND LAPLACE
TRANSFORMS
Among the various methods of operational calculus
used to solve transient problems, one of the most
efficient makes use of the Laplace transform.
If
we have a function
v
=
f(t),
then by definition the
Laplace transform is
2
[f(t)]
=
F(p),
where
The inverse transform of
F(p)
is
f(t).
Most of the
mathematical functions encountered in practical work
fall in the class for which Laplace transforms exist.
Transforms of several functions are given in Chapter
46.
In the following,
an
abbreviated symbol such as
%
[i]
is used instead of
2
[i(t)]
to indicate the Laplace
transform of the function
i(t).
The electrical (or other) system for which a solution
of the differential equation is required is considered

6-20
REFERENCE
DATA
FOR ENGINEERS
only in the time domain
t
2
0.
Any currents or voltages
existing at
t
=
0,
before the driving force is applied,
constitute initial conditions. Driving force is assumed to
be
0
when
t
<
0.
Example
Take the circuit of Fig.
20,
in which the switch is closed
at time
t
=
0.
Before the closing of the switch, suppose
the capacitor is charged; then at
t
=
0,
we have
v
=
Vo.
It is required to find the voltage v across capacitor
C
as a
function of time.
Since i
=
dq/dt
=
C(dv/dt), the differential equation
of the circuit in terms of voltage is:
e(t)
=
v
+
Ri
=
v
+
RC(dv/dt)
0%.
5)
where
e(t)
=
E,.
Referring to the table of transforms, the applied
voltage is
Eb
multiplied by unit step, or
EbS-,(t);
the
transform for this is
Eb/p.
The transform of
v
is
3
[VI.
That of RC(dv/dt) is
RC[p
3
[VI
-
v(O)], where v(0)
=
V,
=
value of v at
t
=
0.
Then the transform of Eq.
(5)
is:
Eb/p
=
3
[VI
+
RC[p
3
[VI
-
vo]
Rearranging and resolving into partial fractions:
RCVo
Eb
+
~
%
[VI
=
p(1
+
RCp)
1
+
RCp
Now we must determine the equation that would
transform into
Eq.
(6).
The inverse transform of
3
[VI is
v, and those of the terms on the right-hand side are
found in the table of transforms. Then, in the time
domain
t
2
0
v
=
Eb[l
-
exp(-t/RC)]
+
Vo
exp(-t/RC)
(Eq.
7)
This solution is also well known by classical meth-
ods. However, the advantages of the Laplace transform
method become more and more apparent in reducing
the
labor
of
solution
as
the equations become more
involved.
Fig.
20.
Series
R-C
circuit.
Circuit Response Related to
Unit Impulse
Unit impulse (see Laplace transforms) has the dimen-
sions of time-'. For example, suppose a capacitor of
1
microfarad is suddenly connected to a battery of
100
volts, with the circuit inductance and resistance negligi-
bly small. Then the current is coulomb multiplied
by unit impulse.
The general transformed equation of a circuit or
system may be written
3
[il
=
Jl(p)
3
[el
+
44~)
0%.
8)
Here
3
[i] is the transform of the required current (or
other quantity) and
%
[e] is the transform of the applied
voltage or driving force
e@).
The transform of the initial
conditions, at
t
=
0,
is included in
Jl(p).
First considering the case when the system is initially
at rest,
flp)
=
0.
Writing
i,
for the current in this case
Now apply unit impulse
So@)
(multiplied by
1
volt-second), and designate the circuit current in this
case by
B(t)
and its transform by
3
[B].
The Laplace
transform of
So@)
is
1,
so
3
PI
=
&PI
(Eq.
10)
Equation
(9)
becomes, for any driving force
3
[i,]
=
3
[B]
3
[e]
(Eq. 11)
Applying the convolution function (Laplace trans-
form)
i,
=
[
B(t
-
A)
e
(A)
dA
=
[
B(A)
e
(t
-
A) dA
(Es. 12)
To this there must be added the current io due to any
initial conditions that exist. From
(8)
23
Pol
=
~P)
(Eq. 13)
Then
io
is
the inverse transform of
ib(p),
Circuit Response Related to
Unit Step
Unit step is defined and designated
S-,
(t)
=
0
for
t
<
0
and equals unity for
t
>
0.
It has no dimensions. Its
Laplace transform is
Up.
Let the circuit current be
designated
A(t)
when the applied voltage is
e
=
S-,(t)
X
(1
volt). Then, the current i, for the case when the

FUNDAMENTALS
OF
NETWORKS
6-21
system is initially at rest, and for any applied voltage
e@),
is
given by any of
i,
=
A(t)
e
(0)
+
I,'
A(t
-
A)
e'
(A)
dh
=
A(0)
e
(t)
+
[
A'(f
-
A)
e
(A)
dh
=
A(0)
e
(t)
+
1
A"
(A)
e
(t
-
A)
dA
(Eq. 14)
where
A'
is the first derivative
of
A
and similarly for
e'
of
e.
As
an example, consider the problem of Fig. 20 and
Eqs.
(5)
to (7) above. Suppose
Vo
=
0,
and that the
battery is replaced by a linear source
e(t)
=
Et/Ti
where
TI
is the duration of the voltage rise in seconds.
By Eq. (7), setting
E,
=
1
A(t)
=
1
-
exp(-t/RC)
Then using the first equation in (14) and noting that
e
(0)
=
0,
and
e'(t)
=
E/Ti
when
0
5
t
5
TI, the solution
is
v
=
(Et/Ti)
-
(ERC/Tl)[l
-
exp(-t/RC)]
This result can, of course, be found readily by direct
application of the Laplace transform to Eq.
(5)
with
e(t)
=
Et/Tl.
Heaviside Expansion Theorem
When the system is initially at rest, the transformed
equation is given by Eq. (9) and may be written
2?
[io1
=
[M(p)/G(p)l
9
[el
(Eq. 15)
M(p)
and
G(p)
are rational functions of
p.
In the
following,
M(p)
must be of lower degree than
G(p),
as
is
usuaIIy the case. The roots of
G(p)
=
0
arep,, where
r
=
1, 2,
.
.
,
n,
and there must be
no
repeated roots.
The response may be found by application of the
Heaviside expansion theorem.
For a force
e
=
E,,,
exp(jut) applied at time
t
=
0
(Eq. 16a)
The first term on the right-hand side of either form of
(16)
gives the steady-state response, and the second,;
term gives the transient. When
e
=
E,,,
coswt, take
the real part of (16), and similarly for sinwt take the
imaginary part.
Z(p)
is defined in Eq. (19). If the
applied force is the unit step, set
w
=
0
in Eq. (16).
Application
to
Linear Networks
The equation for a single mesh is of the form
A,(d"i/dt")
+
* *
+
Al(di/dt)
+
A,+
+
B
i
dt
=
e(t)
(Eq.
17)
System Initially
at
Rest-Then, Eq. (17) trans-
forms into
where the expression in parentheses is the operational
impedance, equal to the alternating-current impedance
when we set
p
=
jw.
If there are
rn
meshes in the system, we get
rn
simultaneous equations like (17) with
rn
unknowns
i
,
i2,
* *
,
i,.
The
m
algebraic equations like
(18)
are
solved for
3
[ill,
etc., by means of determinants,
yielding an equation of the form
of (15)
for each
unknown, with a term on the right-hand side for each
mesh in which there is a driving force. Each such
driving force may of course bc treated separately and
the responses added.
If any two meshes are designated by the letters
h
and
k,
the driving force
e(t)
being in either mesh and the
mesh current
i(t)
in the other, then the fraction
M(p)/
G(p)
in
(15)
becomes
where
Yhk(p)
is the operational transfer admittance
between the two meshes. The determinant of the system
is
G(p),
and
Mhk(p)
is the cofactor of the row and
column that represent
e(t)
and
i(t).
System Not Initially
at
Rest-The transient due
to the initial conditions is solved separately and added
to the above solution. The driving force is set equal to
zero
in
Eq.
(17),
e(t)
=
0,
and each term
is
transformed
according to
n
2?
[dni/dtn]
=
p"%e[i]
-
pn-r[dr-li/dtr-l]l=O
r=
1
(Eq.
20a)
