Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


6-22
REFERENCE
DATA
FOR ENGINEERS
where the last term in each equation represents the
initial conditions. For example, in Eq. (20b) the last
term would represent, in an electrical circuit, the
quantity of electricity existing on a capacitor at time
t
=
0,
the instant when the driving force
e(t)
begins to act.
Resolution into Partial Fractions-The solution
of the operational form of the equations of a system
involves rational fractions that must be simplified before
the inverse transform is found. Let the fraction be
h(p)/g(p)
where
h(p)
is of lower degree than
g(p),
for
example
(3p
+
2)/(p2
+
5p
+
8).
If
h(p)
is of equal or
higher degree than
g(p),
it can be reduced by division.
The reduced fraction can be expanded into partial frac-
tions. Let the factors
of
the denominator be
(p
-
p,)
for the
n
nonrepeated roots
pr
of the equation
g(p)
=
0,
and
(p
-
p,)
for a root
pa
repeated
m
times.
There is a summation term for each root that is
repeated. The constant coefficients
A,
and
B,
can be
evaluated by reforming the fraction with a common
denominator. Then the coefficients of each power of
p
in
h(p)
and the reformed numerator are equated and the
resulting equations solved for the constants. More
formally, they may be evaluated by
where
andf('-')(p,) indicates that the
(r
-
1)th derivative
of
f(p)
is to be found, after which we set
p
=
Fractions of the form (Alp
+
A2)/(p2
+
o
)
or, more
generally
4..
where
b
>
u2
and
o2
=
b
-
a2
need not be reduced
further. From the Laplace transforms the inverse trans-
form of (22a) is
exp(-@(A
COSW~
+
B
sinor)
where
(Eq. 22b)
h(-a
+
jw)
g'(-a
+
jw)
h(-a
-
jo)
g'(-a
-
jo)
A=
+
(Eq.
22c)
Similarly, the inverse transform of the fraction
is exp (-@(A coshat
+
B
sinhat), where
A
and
B
are
found by (22c) and (22d), except that
jw
is replaced by
a
and the coefficientj is omitted in the expression for
B.

7
Fourier
Waveform
Analysis
Revised
by
David
C.
Munson,
Jr.
Fourier Transform of a Function
7-2
Fourier Series
7-2
Real Form
of
Fourier Series
Complex Form
of
Fourier Series
Average Power
Odd
and Even Functions
Odd
or Even Harmonics
Pulse-Train Analysis
7-9
Spectral Analysis
7-10
7-1

7-2
REFERENCE DATA FOR ENGINEERS
FOURIER TRANSFORM OF
A
FUNCTION
The Fourier transform,
F,
of function
f
is defined by
the integral (where
x
and
y
are real variables)
~(y)
=
jym
f(x)
exp (--j2vv) dx
provided this integral exists.
that
f
be absolutely integrable; that is
A sufficient, but not necessary, existence condition is
An important example of a function that has a Fourier
transform even though it is not absolutely integrable is
(sim)/x.
In general,
F
and
f
may be complex. Letting
f(x)
=
&(x)
+
&(x),
where6 andJ are real-valued, one has
F(y)
=
/:m
[f,(x)
cos2~y.x
+
J(x)
sin2~yxIdx
-
j
[f,(x)
sin2n-y~
-
J(x)
cos2~yx]dx
Conversely, the function
f,
whose Fourier transform
is
a given function
F,
is given by the integral (inverse
Fourier transform)
where it is assumed that, at points of discontinuity of
the integral (if any), the functionf(x) is given the value
f(x)
=
[f(X+)
+f(x-)1/2
The functionsf(x’) andf(x-) are the limits off(x
+
t)
as
1
approaches
0
through positive and negative values,
respectively.
Letting F(y)
=
F,(y)
+
jF,(y), one has
[F,(y) sin2~yx
+
&(y) cos2~yx]dy
+
j
Jrm
In many engineering applications it is customary to
denote the variable y as “frequency”; in most cases
x
represents time or space.
If the radian frequency
w
=
2~y is introduced as
a
variable, the definitions
of
the Fourier transform and of
its
inverse are written as
F(w/2?T)
=
F,(o)
=
/yx
f(x)
exp(-jwx)dx
Properties of the Fourier transform are listed in Table
1.
Table 2 contains normalized graphs of the Fourier
transform (or
its
magnitude) for a number of common
pulse shapes.
FOURIER SERIES
Real Form
of
Fourier Series
A
periodic function with period T, defined by its
values in the intervals -T/2 to
+Ti2
or
0
to
T
can be
written in a Fourier series expansion as
where
wo
=
27r/T, and the coefficients are given by
=
(2lT)
/‘f(x)
0
cos(nwox)dx
Ti
2
B,,
=
(2/T)
/-T/,
f(x)
sin(nwox)dx
=
(2/T)
1‘
f(x)
sin(nwox)dx
0
for
n
=
0,
1,
2;
a
..
An alternative form
of
the above expansion is
m
f(x)
=
(112)CO
+
E
C,cos(nwox
+
$,,)
n=
1
where
C,
=
A0
C,
=
(A:
+
B,2)1’2
cos$,
=
A,/C,
sin$,
=
-B,,/C,
Complex Form
of
Fourier
Series
The Fourier series can
be
written more concisely as

TABLE
1.
PROPERTIES
OF
FOURER TRANSFORM*
Function Fourier Transform
F(y)=JiU
f(x)
exXp(-2vjxy)dx
--P
1.
Definition
3.
Linearity
4.
Translation
or
shifting
theorem
am
.f
I
(4
%f*
(x)
g(x)=f(x-xo),
xo
=real const.
g
(x)
=exp(2?rjyox)f(x),
yo
=real const.
5.
Change
of
scale
g(x)=f(x/u),
a=real const.
6.
Frequency shifting and
change of scale
7.
Interchange
of
function
and transform
8a.
Convolution in x-space
(product
of
Fourier
transforms)
8b.
Convolution in y-space
(product of inverse
Fourier transforms)
g(x)=exp(2mjyox)f(x/a), yo and u=real const.
G(Y)=I~IF[~Y-Yo)I
H=F.G
h=fg
H=F*G
9.
Unit pulse (or
Dim
@)
F(y)=l
(for
ally)
f(x)=
1
(for all
x)
s(
Y)
function)
Continued
on
next page.
U
b

TABLE
1
(CONT).
PROPERTJES
OF
FOURIER
TRANSFORM*
Fourier Transform
Function
tm tm
(AIT)
S(y-n/T)
,I=-"
10.
Peiiodic
train
of
equal
A
C
gx-rrT)
*=-a
pulses
g
(x)
=
d*f/dx"
G(y)=(2rjy)" F(y),
if G(y) exists
1
la. Derivative
in
x-space
llb.
Derivative
in
y-space
&)=(
-2?rjx"f(x)
C(y)=dn
Fldy"
12a.
Integral
in
x-space
12b. Integral in y-space
13.
Symmetry
14.
Complex conjugate
where
F(O)=
\:m
f(x)dx
15.
Area under
the
curve
16a. Parseval's theorem
z
D
Continued on next
page.
rn

TABLE
1
(CONT). PROPERTIES
OF
FOURIER
TRANSFORM*
Function Fourier Transform
17.
initial value theorem
Iff(x)
=
0
for
x
<
0,
is real, and contains no pulses
18. Relationships between
F(Y)
and
FAY)
f(Ot)
=
2
I”
FAY)&
where
F,(y)
=
Re[F(y)]
a)
Iff(x)=O for
x
<
0,
is
real, and contains no pulses
-30
b
--
E
in which the Cauchy principal values of the integrals are taken
*
In the table, functions
of
x
are denoted by lower-case letters and their transforms by the corresponding capital letters.
I
UI
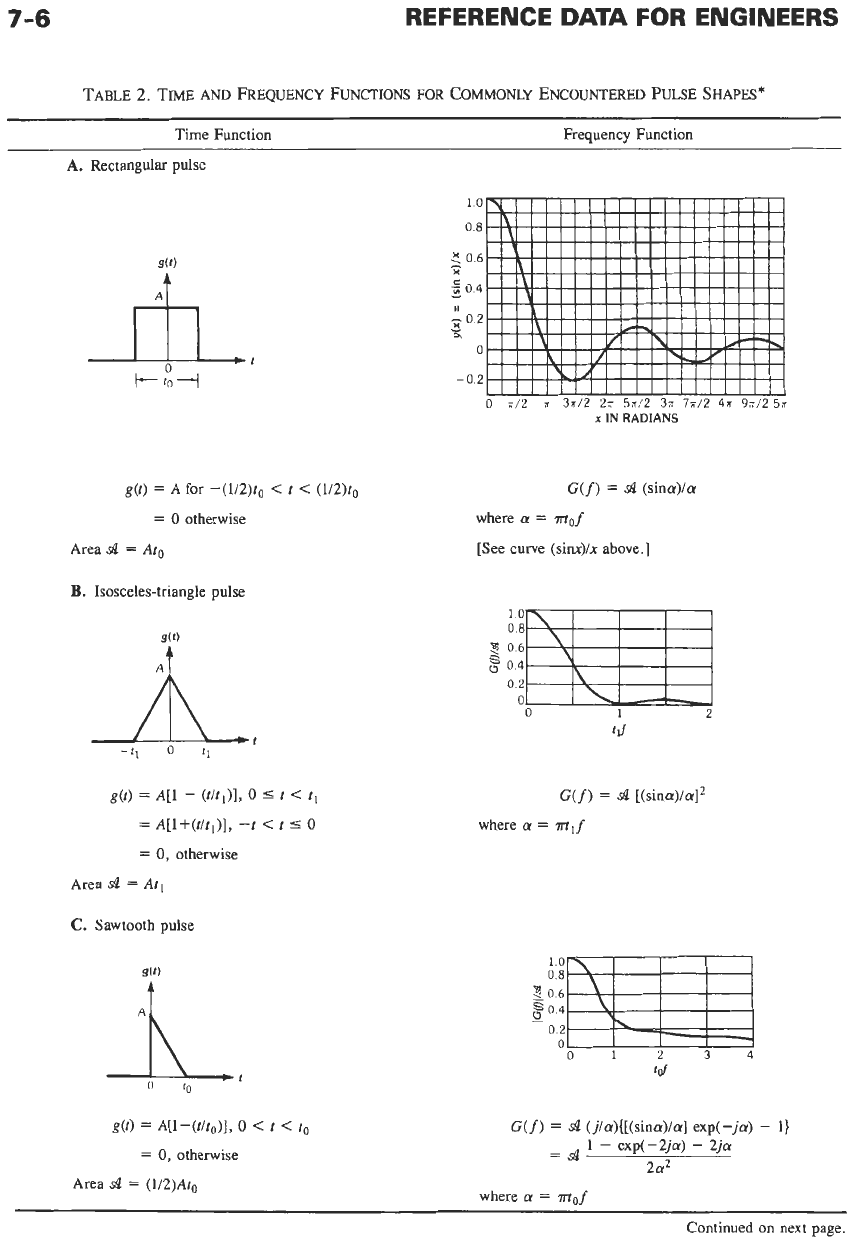
7-6
REFERENCE
DATA
FOR ENGINEERS
TABLE
2.
TIME
AND
FREQUENCY
FUNCTIONS
FOR
COMMONLY
ENCOUNTERED
PULSE SHAPES*
Time Function Frequency Function
A.
Rectangular pulse
g(t)
=
A for -(1/2)to
<
t
<
(1/2)to
=
0
otherwise
Area
SZ
=
Ato
B.
Isosceles-triangle pulse
g(t)
=
A[1
-
(t/tl)],
0
5
t
<
t,
=
A[l+(t/tI)],
-t
<
t
S
0
=
0,
otherwise
Area
94
=
At,
C.
Sawtooth pulse
L.
1.0
0.8
2
0.6
.$
0.4
-
0.2
0
-0
2
X
-
I1
-
0
a/2
T
3s/2
2a
5s/2
3s
7s/2
4s
%/2
5s
x
IN RADIANS
G(f)
=
94
(sina)/a
where
a
=
mof
[See
curve (sinx)/x above.]
10
08
06
$
04
02
0
0
1
2
kf
G(f)
=
94
[(sina)/aI2
where
a
=
m,f
10
08
-
3
06
504
02
0
-
01234
td
g(t)
=
A[l-(t/to)],
0
<
t
<
to
G(f)
=
SZ
(j/a){[(sina)/a] exp(-ja)
-
1)
~
1
-
exp(-2ja)
-
2ja
-
=
0,
otherwise
-
2a2
Area
SZ
=
(1/2)At0
where
a
=
mof
Continued
on
next page.

FOURIER
WAVEFORM
ANALYSIS
7-7
TABLE
2
(CONT).
TIME
AND
FREQUENCY FUNCTIONS
FOR COMMONLY
ENCOUNTERED
PULSE
SHAPES*
Time Function Frequency Function
D.
Any pulse of polygonal form may be represented as a linear combination of waveforms such as
A,
B,
and
C
above
eventually after some shifts in time. The pulse spectrum is the same linear combination
of
the corresponding spectra
(eventually modified according to property
4,
Table 1).
E.
Cosine pulse
g(t)
=
A
cos.rr(t/t0), -(i/2)t0
<
t
<
(1/2)t0
=
0,
otherwise
Area
.d
=
(2/~)Ato
F.
Cosine-squared pulse
=
0,
otherwise
Area
s2
=
(1/2)Ato
G.
Gaussian pulse
Use
curve
of
Fig. 1, Chapter
44
with standard deviation
u=
t,
=
(2
!n2)-”’tMB; At,, 2tMB
10
08
06
2
04
0
-0
2
l3
02
01234
‘of
C(f)
=
d
{[cos(~~)Q]/(~
-
a’)}
where
Q
=
2t0f
For
Q
=
1,
G(f)
=
dn/4
10
08
06
04
02
0
-0
2
01234
U
where
a
=
tof
For
a
=
1,
G(f)
=
(1/2)d
Use
curve
of
Fig. 1, Chapter
44
with standard deviation
u
=
fi
=
1/2m1
=
(21112)“’/?rAt~~;
f3d~
=
2”’ h2/TAta~
Area
s2
=
(2?r)’/’AtI
=
(1/2)(~/ln2)”~ AAt@B
=
(1/2)(~/1n2)“’ AAtMB
X
exp[-(?r2/4 ln2)(fAta~)’]
Continued on next page.
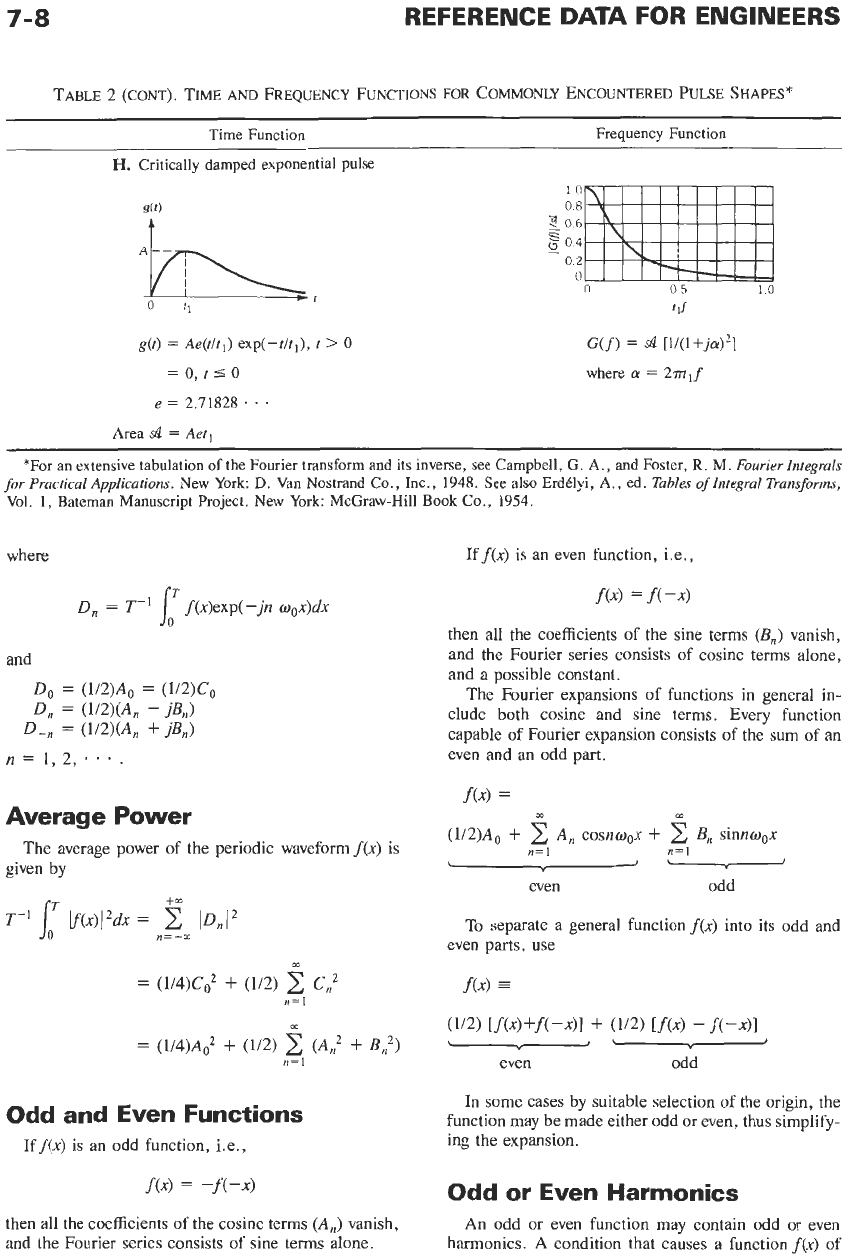
7-8
REFERENCE
DATA
FOR ENGINEERS
TABLE 2 (CONT). TIME
AND
FREQUENCY FUNCTIONS
FOR
COMMONLY ENCOUNTERED PULSE
SHAPES"
Time Function Frequency Function
H.
Critically damped exponential pulse
10
08
-
?
06
2
04
02
0
-
0
05
10
'If
g(t)
=
Ae(t/t,)
exp(-tlt,),
t
>
0
G(f)
=
1
[l/(l+ja)']
=O,tSO
where
a
=
2.rrt1f
e
=
2.71828
.
. .
Area
Se
=
Aet,
*For
an
extensive tabulation
of
the
Fourier transform and its inverse, see Campbell, G. A.,
and
Foster,
R.
M.
Fourier Integrals
for Practical Applications.
New York:
D.
Van Nostrand Co., Inc., 1948.
See
also Erddyi, A,,
ed.
Tables
of
Integral Transforms,
Vol. 1, Bateman Manuscript Project. New York: McGraw-Hill Book Co., 1954.
where
D,
=
T-'
f(x)exp(-jn
wox)dx
r
and
Do
=
(112)Ao
=
(1/2)Co
D,
=
(1/2)(A,,
-jB,)
D-,
=
(1/2)(A,
+jB,)
n=l,2;..
.
Average Power
The average power of the periodic waveform f(x) is
given by
m
=
(1/4)C:
+
(1/2)
2
C:
fl=l
cf
=
(1/4)A;
+
(1/2)
(A:
+
B:)
,=I
Odd and Even Functions
Iff(x) is an odd function, i.e.,
f(x)
=
?(-XI
then all the coefficients of the cosine terms (A,) vanish,
and the Fourier series consists of sine terms alone.
Iff(x) is an even function, i.e.,
f(x)
=
f(-4
then all the coefficients of the sine terms
(B,)
vanish,
and the Fourier series consists
of
cosine terms alone,
and a possible constant.
The Fourier expansions of functions in general in-
clude both cosine and sine terms. Every function
capable of Fourier expansion consists of the
sum
of an
even and an odd
part.
f(x)
=
m
m
(1/2)A0
+
2
A,
cosntwox
+
B,
sinnwox
n=
1
n=l
'M
even odd
To separate
a
general functionf(x) into its odd and
even parts, use
(1/2) If(x)+f(-x)l
+
(W [f(4
-
f(-x)l
p-
even odd
In some cases by suitable selection of the origin, the
function may be made either odd or even, thus simplify-
ing the expansion.
Odd
or
Even Harmonics
An odd or even function may contain odd or even
harmonics. A condition that causes
a
function ,f(x) of
FOURIER WAVEFORM ANALYSIS
7-9
period
T
to have only odd harmonics in its Fourier
expansion is
the presence of particular odd or even harmonics is
unchanged by such a shift.
PULSE-TRAIN ANALYSIS
every interval
T,
a periodic waveform
f(x)
=
-f(x
+
T/2)
A
condition that causes a function
f(x)
of
period
T
to
have only even harmonics in the Fourier expansion is
If the pulse defined by the function
g(t)
is repeated
f(x)
=
f(n
+
T/2)
n=-3:
To separate a general functionf(x) into its odd and even
harmonics, use
results with period
T
and repetition frequency
F
=
1/T
(see
A
and
B
in Table
3).
This pulse train may be expressed as a convolution
product
f(4
=
(1/2)[f(4
+
f(x
+
m1
+
(W[f(X)
-
f(n
+
m1
+m
Y(0
=
[
c
-
nT)I*g(d
'P
even harmonics odd harmonics
n=-30
A
periodic function may sometimes be changed from
odd to even (and vice versa)
by
a shift
of
the origin, but
and, from application of properties
8
and 10 (Table
I),
its Fourier transform is
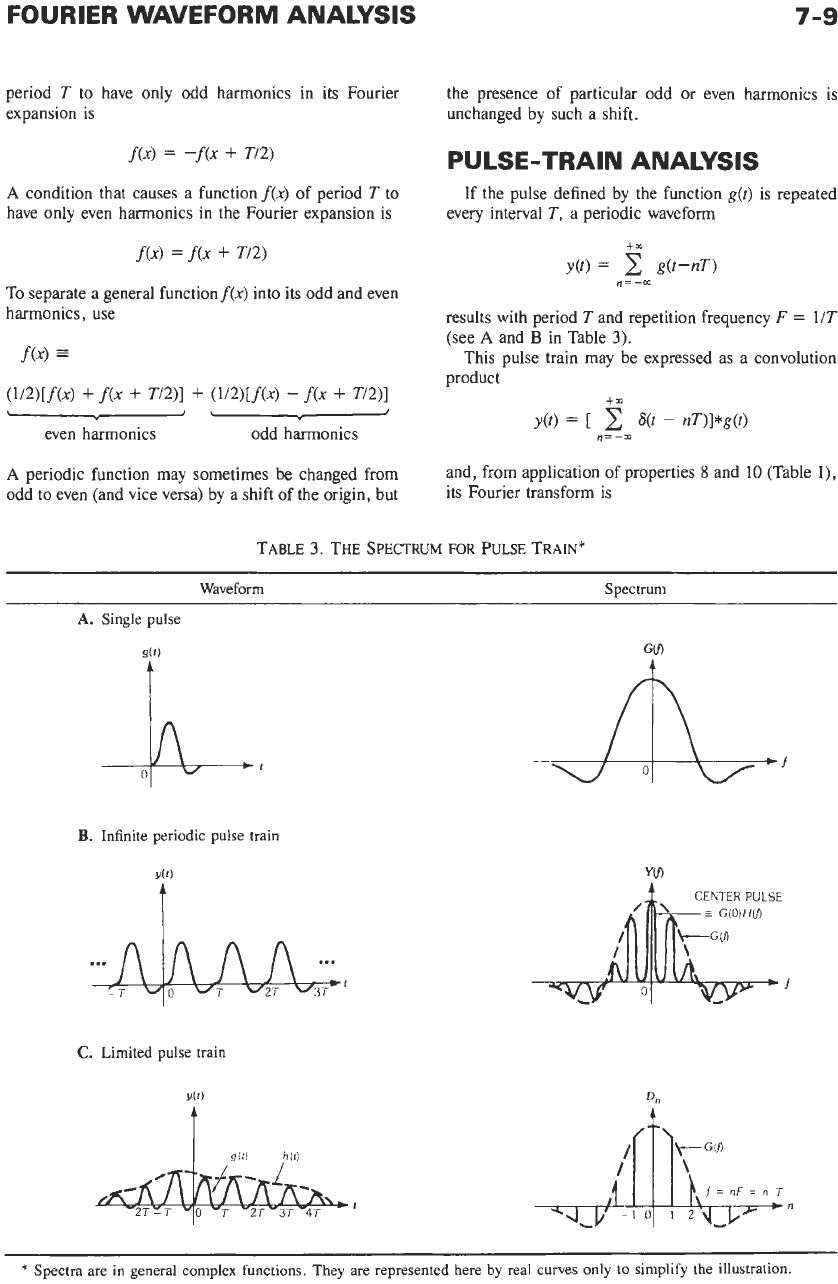
TABLE
3.
THE SPECTRUM
FOR
PULSE TRAIN*
Waveform Spectrum
A.
Single pulse
B.
Infinite periodic pulse train
C.
Limited pulse train
t
Sit)
hili
A
CENTER
PULSE
'7r\s
G(O)H@
+-G
cn
I
'I
I
*
Spectra are in general complex functions. They are represented here by real curves only
to
simplify the illustration.
