Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


24-6
REFERENCE
DATA
FOR ENGINEERS
QUADRATURE
#
IN-PHASE
Fig.
5.
A
16-QASK
signal constellation
do
=
+
1 and
d,
=
-
1.
Based on the latter choice for
dk,
the BPSK signal can be defined by
where
a(t)
=
1
for all
t
and
The data symbol bk is
dk
if
k
is
to be sent in the nth time
interval. This formulation corresponds to phase modu-
lation by a sequence of rectangular pulses of duration T
with amplitudes (7rI2)bn. The resulting signal
s(t)
is
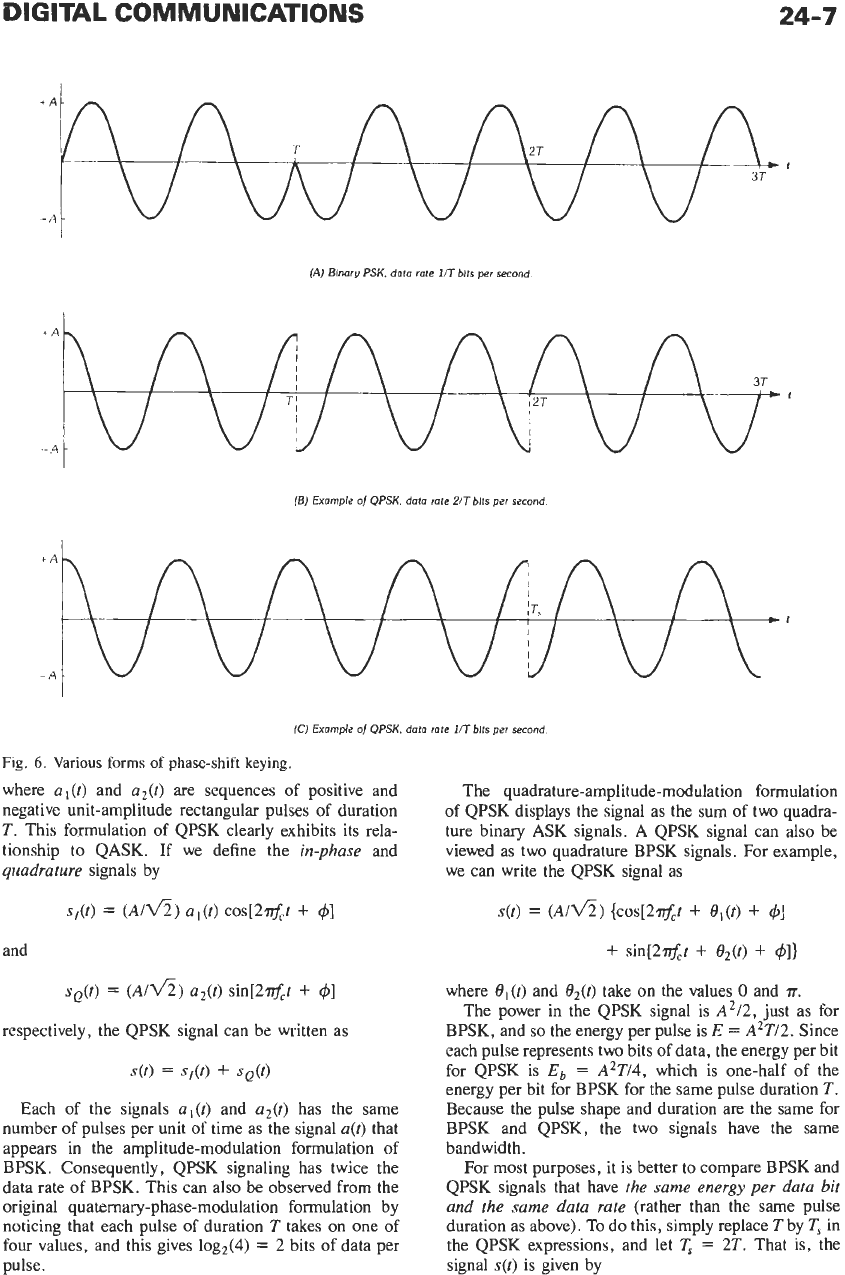
illustrated in Fig. 6A for the data sequence
bo
=
-
1,
bl
=
+
1,
and
b2
=
+
1. This illustration is forf,T
=
2
and
4
=
0.
Viewed as binary amplitude modulation, the BPSK
signal can be expressed in a form that reveals its
connection with binary ASK. Let
O(t)
=
0
for all
t
and
use the amplitude to convey the information by defining
40
=
bnp-r(t
-
nT)
m
n=-m
Thus,
0
is
sent by transmitting
s(t)
=
A
cos[2?rf,t
+
41
and
1
is sent by transmitting
~(t)
=
-A
cos[2.llf,t
+
41
This formulation of binary PSK corresponds to ampli-
tude modulation by a sequence of rectangular pulses of
duration T with amplitudes
+
1
and
-
1.
However, it is
equivalent to phase modulation of the form
s(t)
=
A
COS[2%$t dk(71.12)
41
with do
=
0
and
d,
=
2.
Although the modulator implementations suggested
by these two formulations are quite different, the
resulting signal sets are mathematically equivalent. In
particular, it is clear from either of these formulations
that the BPSK signals representing the binary digits
0
and 1 form an antipodal signal set. Notice also that for
each of these representations the energy per data pulse
is
E
=
A2T/2.
Quadriphase Shift Keying
(QPSK)
Binary PSK can be generalized by allowing the phase
waveform to take on more than two values. The QPSK
signal
is
of the same basic form as BPSK, except that
quaternary modulation is employed instead of binary
modulation. Thus the transmitted signal for the interval
[nT,
(n
+
1)T] can be written as
S(t)
=
A
COS[2'7&t
ek
41
where
k
denotes the message to be sent in the nth
interval
(k
=
0,
1,2, or 3). The four different values for
Ok
must be separated by 71./2 radians. For example, we
can let
{Qk
=
0,
1,2,3} be the set {0,71./2,
T,
3d2) or
the set (d4, 3d4, 5~14, 771.14).
As
with BPSK, the
values themselves are unimportant, but the differences
are constrained.
The QPSK signal can be expressed as
s(t)
=
A
cos[2MCt
+
0(t)
+
41
The phase modulation
O(t)
is a sequence of rectangular
pulses
of
duration T and amplitudes (7r/2)bn with
bn
=
0,
1, 2, or 3. This signal is illustrated in Fig. 6B for the
data sequence
bo
=
0,
bl
=
2, and
b2
=
3. As in Fig.
6A,f,T
=
2 and
4
=
0.
The QPSK signal can
also
be viewed as quadrature
amplitude modulation by writing
s(t)
=
A
cosp.rrf,t
+
e(t)
+
41
as
s(t)
=
A
{cOs[e(t)l ~0~[2.rrf,t
+
41
-sin[e(t)] sin[2.?rf,t
+
4]}
If
e(t)
takes on values in the set (71.14, 371.14, 571./4,
771./4}, then cos[O(t)] is either
+
l/.\/Z
or
-
l/.\/Z,
and
sin [e(t)] takes on the same two values. Thus
s(t)
can be
written as
s(t)
=
(Alfi)
(a,(t)
cos[2.rrf,t
+
41
+
a,@)
sin[2.rrf,t
+
411
DIGITAL
COMMUNICATIONS
24-7
(A)
Binary
PSK,
data
rate
UT
bits
per
second.
(B)
Example
of
QPSK,
data
rate
ZIT
bits
per
second
(C)
Example
of
QPSK,
data
rnte IIT
bits
per
second.
Fig.
6.
Various
forms
of phase-shift keying.
where
al(t)
and
a,@)
are sequences of positive and
negative unit-amplitude rectangular pulses of duration
T.
This formulation of QPSK clearly exhibits its rela-
tionship to QASK. If we define the
in-phase
and
quadrature
signals by
The quadrature-amplitude-modulation formulation
of QPSK displays the signal
as
the sum of two quadra-
ture binary ASK signals. A QPSK signal can
also
be
viewed as two quadrature BPSK signals. For example,
we can write the QPSK signal as
s,(t)
=
(A/l/z)
al(t)
cos[2@t
+
41
s(t)
=
(Alfi) {c0~[2?rf,t
+
O,(t)
+
41
and
+
~in[2$~t
+
e&)
+
4]}
se(t)
=
(~/l/z)
a2(t)
sin[~$~t
+
41
respectively, the QPSK signal can be written as
s(t)
=
sdt)
+
Sf$)
Each of the signals
a,@)
and
a#)
has the same
number of pulses per unit of time as the signal
a(t)
that
appears in the amplitude-modulation formulation of
BPSK. Consequently, QPSK signaling has twice the
data rate of BPSK. This can also be observed from the
original quaternary-phase-modulation formulation by
noticing that each pulse of duration T takes on one of
four values, and this gives log2(4)
=
2
bits of data per
pulse.
where
O,(t)
and
O,(t)
take on the values
0
and
T.
The power in the QPSK signal is A2/2, just as for
BPSK, and
so
the energy per pulse is
E
=
A2Ti2. Since
each pulse represents two bits of data, the energy per bit
for QPSK
is
E,
=
A2T/4, which is one-half of the
energy per bit for BPSK for the same pulse duration
T.
Because the pulse shape and duration
are
the same for
BPSK and QPSK, the two signals have the same
bandwidth.
For most purposes, it is better to compare BPSK and
QPSK signals that have
the same energy per data bit
and
the same data rate
(rather than the same pulse
duration as above).
To
do this, simply replace
T
by
T,
in
the QPSK expressions, and let
T,
=
2T.
That
is,
the
signal
s(t)
is given by

24-8
REFERENCE
DATA
FOR ENGINEERS
=
A
COS[^^^^
+
e(t)
+
41
as before, but now the phase modulation
O(t)
is a
sequence of rectangular pulses of duration
T,
=
2T,
rather than
T.
The amplitudes of these pulses are still
given by
(55-/2)b,
with
b,
=
0,
1, 2, or
3;
however, the
sequence
(b,)
is
now transmitted at the rate of one
quaternary symbol every
T,
seconds. This signal is
illustrated in Fig.
6C
for
bo
=
0
and
bl
=
2,
withf,T
=
2 and
4
=
0.
Because a QPSK pulse of duration
T,
provides two
bits of data, the data rate of a QPSK signal that uses
pulses of duration
T,
is
RqpsK
=
2/T,
=
1/T
bits per second. If the digital data.consists of a single
sequence of binary digits, half of the data bits can be
modulated onto the in-phase component and half onto
the quadrature component.
Since 1/T is also the data rate for a BPSK signal with
pulse duration T, these two forms of PSK modulation
can now be compared on the basis of the same data rate.
In this case, the energy per pulse for QPSK is given by
E
=
A2T,/2
which is equivalent to an energy per bit of
E,
=
A2Ti2
the same as BPSK. The pulse shapes for QPSK and
BPSK are the same, but the pulse duration for QPSK is
T,
=
2T,
twice that for BPSK. This means the QPSK
signal has one-half the bandwidth of the BPSK signal.
In summary, if QPSK and BPSK are compared for
the
same
data
rate, BPSK requires twice the bandwidth
of QPSK. If the two signals have the
same data rate
and
equal
power, they also have the same energy per data
bit.
Offset Quadriphase Shift
Keying (OQPSK)
The OQPSK signal can be defined by replacing
8,
(t)
with
e,(t
+
T)
in the quadrature-phase-modulation
formulation of QPSK. That is, OQPSK can be repre-
sented in terms
of
two quadrature BPSK signals as
~(t)
=
(~~'51
COS[^&^
+
e,(t
+
T)
+
41
+
sin[2Mct
+
e,(t)
+
4]}
where
0,
(t)
and
e,@)
are sequences of pulses of duration
T,
=
2T as in the preceding subsection. Since the
amount of the offset is one-half the pulse duration, the
phase transitions of the in-phase and quadrature compo-
nents of the OQPSK signal are separated in time by T
seconds.
The OQPSK signal can
be
represented as quadrature
amplitude modulation with the baseband signal of the
in-phase component offset by T seconds relative to the
baseband signal of the quadrature component. Thus,
the amplitude-modulation representation of OQPSK
is
s(t)
=
ai^)
{al(t
+
T) cos[2njct
-I-
$1
+
a2(0
sin[2.rrf,t
+
$13
where
al(t)
and
a,@)
are as in the preceding subsection.
Notice that the baseband signal for the in-phase compo-
nent can change polarity at times
nT
for odd integers
n
only, but the transitions of the baseband signal for the
quadrature component are at times
nT
for even values of
n
only. This is an important feature of OQPSK for
band-limited channels with nonlinearities.
A
band-
limited version of QPSK or BPSK has an envelope that
may
go
to zero when the in-phase and quadrature
signals switch polarity at the same time; the offset
in
OQPSK leads to a more nearly constant envelope for
the band-limited signal.
If the OQPSK signal is expressed in the form
s(t)
=
A
C0s[2njct
+
e(t)
+
$1
the phase
O(t)
can change every T seconds, whereas the
phase shifts in QPSK occur only at 2T-second intervals.
However, for OQPSK the magnitudes of the phase shifts
are limited to
0
or 55-12 only. Phase shifts for QPSK can
have magnitudes
0,
55-12, or
55-.
Minimum-Shift Keying (MSK)
The MSK signal can be considered as a special case
of offset quadrature amplitude modulation in which the
baseband waveform is the sine pulse
v(t)
=
sin(55-tti2T)pZT(t). Thus the MSK signal can be written
as
s(t)
=
A
{a,@
+
T)
cos[255$t
+
$1
+
4)
sin[2@
+
41)
where
al(t)
and
a2(t)
are sequences of sine pulses of
duration 2T. That is, for each
i(i
=
1
or
i
=
2)
X
Uj(t)
=
c_
b;,,v(t
-
2nT)
,=-x
where
(b;)
=
.
.
.
,
bi,a,
bi,l,
bit?,
. . .
is a binary data
sequence. Minimum-shift keying can also be viewed as
continuous-phase frequency-shift keying (discussed in a
later subsection).
Binary Frequency-Shift Keying
FSK)
Binary
FSK
signals are of the form
~(t)
=
A
cos[2eCt
+
e(t)l

DIGITAL COMMUNICATION§
24-9
where the modulation
O(t)
is defined as follows. If
0
is
the bit
to
be transmitted in the nth interval,
and if 1 is sent.
Thus, the signal
s(0
=
A
COS[2.rr(f,
+
fd)t
+
401
represents a
0
for the nth interval, and the signal
s(6
=
A
COSP.rr(f,’
-
fd)t
+
411
represents a
1.
The quantity
fd
is called the frequency
deviation, and the parameter
h
=
2fdT is called the
deviation ratio or modulation index for the FSK signal
set. The FSK signals may be generated by switching
between two oscillators or by applying a binary base-
band signal at the input of a voltage-controlled oscillator
In general, the phase angles
4k
are arbitrary, and
4o
need not be related to
4,
in
any
way. If the FSK signals
are obtained by switching between two oscillators, one
at frequency
f,
+
fd
and one at frequency
f,
-
fd,
the
phase angles
Cb0
and represent the phases of these
oscillators at time
t
=
0.
Alternatively, the FSK signals
may be generated by applying a baseband signal to a
VCO (or another frequency-modulation circuit), in
which case the phase angles
4o
and
4,
may be related.
The signals in FSK systems are often referred
to
as
“tones,” and the two signals are distinguished by
calling one of them
“mark”
and the other “space.”
The convention followed here is to refer to the signal at
frequency
f,
+
fd
as the space and the signal at
frequency
f,
-
fd
as the mark (the binary digit
0
is
transmitted as a space, and the binary digit
1
is
transmitted as a mark).
If 2f,T and 2fdT are integers, the mark and space
signals form an orthogonal signal set for
all
values of
+o
and It is often the case thatf,T
>>
1.
Under this
condition, the signals are approximately orthogonal if
2fdT is an integer or iffdT
>>
1.
If 2f,T and
2fdT
are
integers or if
(f,
-
fd)T
>>
1,
the energy per data bit is
A2T12.
For
certain applications, it
is
necessary to generalize
the above formulation
of
FSK
by introducing a phase
angle
+(n)
that depends on the interval in which the
signal is transmitted. To send a
0
in the nth interval, the
transmitted signal for
nT
5
t
<
(n
+
1)T
is
(VCO).
=
A
cosP.rr(f,
+&It
+
4(n)
+
401
and to send a
1
in this same interval, the signal is
s(t)
=
A
~0~[2.rr(f,
-
fd)t
+
4(n)
+
411
FSK signals in frequency-hopped spread-spectrum sys-
tems, for example, where the phase
$(n)
represents a
phase shift introduced by noncoherent frequency hop-
ping.* This generalization is also required for the
description of certain continuous-phase FSK modula-
tion schemes.
Continuous-Phase Frequency-
Shift Keying (CPFSK)
Continuous-phase FSK signals are of the form
s(t)
=
A
~0s[2.rrf,t
+
e(t)]
just as for other types
of
FSK signals. However, for
CPFSK the phase modulation
O(t)
is a continuous
function oft. In order to describe CPFSK modulation,
it is sufficient to consider only the case in which
(Po
=
4,
=
0.
This is because the phase angles
4o
and
41
can
always be absorbed in the phase modulation
O(t)
for
CPFSK signals.
The signal
O(t)
is defined as follows. Suppose
b,
is
the data symbol to be sent in the nth interval, and
bn
is
either
+
1
or
-
1.
The phase modulation is
e(t)
=
2574fdt
+
&n)
for
nt
5
t
<
(n
+
l)T.
The phase angles
4(n)
are such
that the phase
is
continuous from one interval
to
the
next. In order to make the phase continuous at time nT,
the phase angles
+(n)
and
+(n
-
1)
must satisfy
2~b,fdnT
+
4(n)
=
2~b,-ifdnT
+
4(n
-
1)
which is equivalent to the condition
4(n)
=
2.rr(bn-1
-
bn)fdnT
+
4(n
-
1)
In other words,
&n)
=
+(n
-
1)
if the two successive
data symbols
b,-,
and
b,
are the same, but
&n)
and
4(n
-
I)
differ by 4ednT radians if these two data
symbols are different.
The simplest CPFSK signal
is
obtained for the case in
which the modulation index
h
=
2fdT is an integer. For
this case, 4$dnT is an integer multiple of 257, and
+(n)
=
4(n
-
1)
modulo 257, regardless
of
whether the
successive data symbols are the same or different. But
phase‘gngles that differ by integer multiples of 257 are
the same for our purposes,
so
we can let
4(n)
=
4,
where
4
is a constant phase (independent
of
n).
No
phase changes are required in order to make
O(t)
continuous provided the modulation index
is
an integer.
Another modulation index of considerable interest
for CPFSK is 1/2. For
h
=
112, the frequency deviation
isfd
=
114T,
and the condition for continuous phase is
&n)
=
m[(b,-,
-
b,)/2]
+
&n
-
1)
This generalization is required in order to characterize
*
Reference
29.

24-
10
REFERENCE
DATA
FOR ENGINEERS
If the successive data bits b,-, and b, are the same, the
phase angles
+(n
-
1) and
4(n)
are
also
the same. If the
successive data bits are different, b,-,
-
b, is either +2
or -2, and
so
the phase angles must differ by an integer
multiple of
T
radians. It follows that if
NO)
=
0
and
2f,T is an integer, or iff,T
>>
1, the mark and space
signals are orthogonal. It is important to realize that
orthogonality is obtained for
h
=
1/2 only if the phases
in successive intervals are controlled.
From the relationship
B(t)
=
2~b,f,t
+
4(n)
which holds for
nT
5
t
<
(n
+
1)T,
it follows that
13(nT)
=
2~b,.b,fdnT
+
&z)
Making the substitution for
&n)
from the last equation
into the expression for
qt),
we find that
e(t)
=
2rb,fd(t
-
nT)
+
O(nT)
for nT
5
t
<
(n
+
1)T.
This fact and the continuity
condition imply
e((n
+
1)T)
=
27rb,.b,fdT
+
O(nT)
If we denote B(kT) by
ek
and let
h
=
1/2 in this
expression, it can be written as
e,,,
=
(~/2)b,
+
e,
Similarly, the expression for
e(t)
becomes
qt)
=
(r/2~)b,(t
-
n~)
+
e,
which is valid for
nT
5
t
<
(n
+
1)T.
The CPFSK signal is
s(t)
=
A
{cos[e(t)]cos[2.rrf,t]
-
sin[
qt)]
sin[ 2.rrf,t]}
The above relationships for
e@),
e,,
and
On+,
imply that
if
n
is an even integer and
h
=
1/2,
-sin
O(t)
=
-~in[O,+~]sin[.rr(t
-
nT)/2T]
for nT
I
t
<
(n
+
2)T. Similarly, if
n
is an odd integer
and
h
=
1/2,
cos
e(t)
=
-~os[e,+~]sin[.ir(t
-
nT)/2T]
for
nT
<
t
<
(n
+
2)T. Define the data sequence
(B,)
by
B,
=
-sin
if
n
is an even integer and by
B,
=
-cos
e,+,
if
n
is an odd integer. The data sequence
(B,)
is related
to the original data sequence (b,) by
6,
=
-B,
COS
8,
if
n
is an even integer and by
b,
=
B,
sin
0,
if
n
is an odd integer.
h
=
1/2 the CPFSK signal
s(t)
is of the form
From the above development, we conclude that for
s(t)
=
A
{a,@
+
T)
cos[2?rf,t]
+
nz(l)
sin[2n$t]}
The baseband signals
a,@)
and
az(t)
are given by
ai@)
=
B,,-,sin
[Mi
-
2kT)/2T]
and
az(t)
=
B2k
sin[.ir(t
-
2kT)/2T]
for 2kT
5
t
<
2(k
+
1)T.
A
comparison
of
these last
three equations with analogous equations in the subsec-
tion on minimum-shift keying shows that CPFSK with
modulation index
h
=
1/2 is the same as
MSK.
M-ary Signaling and Multiple
Frequency Shift Keying (MFSK)
The general
M-ary
RF signal set has signals of the
form
sk(t)
=
~a~(t)
coa.rrf,t
+
e,(o
+
4k~
fork
=
0,
1,
. .
.
,
M
-
1. The signals
a&)
and
13,(t)
are baseband signals with bandwidths much smaller
than the carrier frequency
f,
.
The messages are indexed
by the integers
0,
1,
.
.
.
,
M
-
1, and in order to send
the kth message during the nth interval, the signal
s(t)
=
pT(t
-
nT)
sk(t)
is transmitted. (The rectangular pulse
of duration T is defined by
pT(u)
=
1
for
0
5
u
<
T and
pT(u)
=
0
otherwise.)
The
RF
signal set is characterized by the inner
products
Since the amplitude modulation and phase modu-
lation
e&)
are narrow-band signals, the inner products
are (at least approximately) given by
where

DIGITAL COMMUNICATIONS
24-11
and
I$k,j
=
I$k
-
I$j
If
(sk,
sj)
=
0
for all
j
#
k,
the signals form an
orthogonal signal set. One type of orthogonal signal set
is obtained by letting
e&)
=
0
for all
t
and using a set of
orthogonal baseband signals for the amplitude modula-
tion
a&).
Multiple frequency shift keying
(MFSK),
which is
also known as
M-ary
frequency shift keying, is a direct
extension of binary FSK to modulation with more than
two frequency tones. It is also a special case of
M-ary
signaling in which
ak(t)
=
1 and
ek(t)
=
(fk
-f,)t
The resulting signals are of the form
Sk(f)
=
A
cos[2%$f
+
I$k]
In order to send the kth message in the nth interval,
the transmitted signal is
If the frequencies
fk
are such that
fkT
=
nk
for some
integers
no,
n
the M different signals are
orthogonal on each interval
[nT,
(n
+
1)T].
The signals
are at least approximately orthogonal if
lfk
-
BIT
>>
1
for each choice of
j
#
k.
The phases
I$,,, I$,,
.
.
.
,
are arbitrary and, in general, not related to each
other in any way.
.
.
.
,
nM-
Spectra
of
PSK
and
MSK
Signals
By introducing appropriate random time delays and
phase angles, we can model the signal
s(t)
as a
wide-sense stationary random process. The Fourier
transform
of
the autocorrelation function for this ran-
dom process is called the power spectral density, or
simply the spectrum. The spectrum of a signal gives a
measure of the distribution of its power as
a
function of
frequency. For example, the bandwidth
of
a signal is
usually defined in terms of its spectrum (e.g., see
reference
15).
The four digital modulation techniques
considered are three forms
of
phase-shift keying (PSK)
and MSK. The three PSK schemes
are
BPSK, QPSK,
and OQPSK. The data rate in each case is assumed to be
R
=
1/T
bits per second.
The spectrum of the BPSK signal is
where the function
GI
is defined by
Gl(x)
=
[sinc(x)12
=
[sin(~x)/?rx]~
The spectrum of a QPSK signal with data rate
R
=
UT
bits per second is given by
where
The spectrum
of
the OQPSK signal is the same as the
spectrum
of
the QPSK signal. The spectrum of the
MSK signal is
S3U)
=
(A2774){G3[(f
-
f,)
TI
+
G3[(f
+
f,)TII
where the function G3 is defined by
G~(x)
=
{[(4/~r) COS(~TX)]/(~
-
16~'))~
The power in each
of
the PSK and
MSK
signals is
P
=
A2/2. Since the power is equal to the integral of the
power spectral density,
for each
i.
The comparisons below of the spectra of PSK
and MSK signals
are
made on the basis
of
equal power
in the signals. It is also common to compare the signals
on the basis of equal values of
Si(&),
the spectral
density at the carrier frequency (e.g., reference
15),
but
in this case the signals have different power levels.
Notice that the spectra
Sl(f),
S2(f),
and S3(f) are
given in the form
so
that comparisons of these spectra can be made by
comparing the corresponding functions
GI
(x), G2(x).
and G3(x). In fact, iff,T
>>
1 the two components of
the spectrum do not overlap significantly; that is, for
each integer i,
Gi
t(f
-
LIT1
>>
Gj[(f
+
f,)
TI
forf
>
0,
and the reverse inequality holds forf
<
0.
It
follows that
Si(f)
is approximately
si(f)
=
Git(f
-
f,)7'1
for
f
>
0
and
si(f)
=
Gi[(f
+
f,)TI
for
f
<
0.
Consequently, for
fcT
>>
1,
the shape of
spectrum
Si(f)
forf
>
f,
is just the shape of Gi(x) for
x
>
0.
Also notice that Gi(x)
=
Gi(-x).
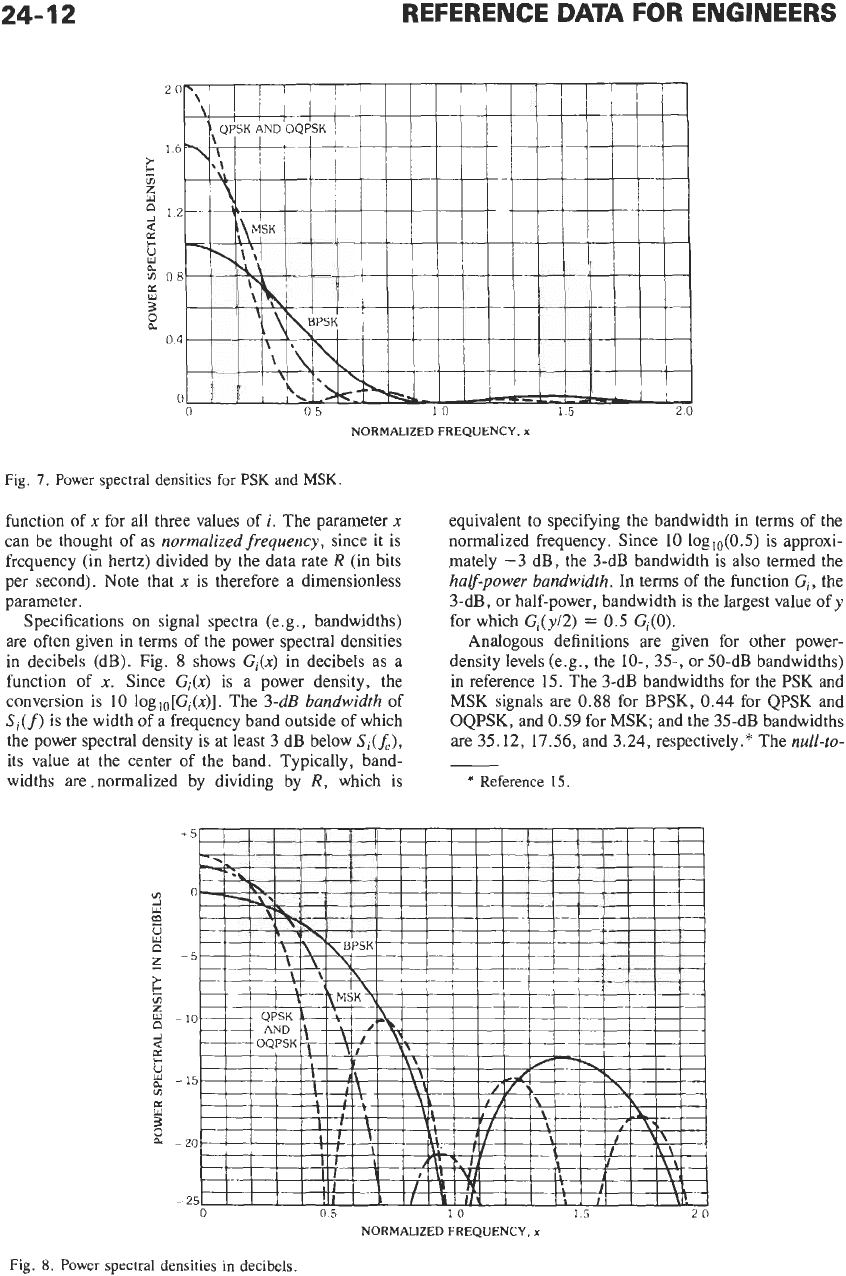
The spectra of BPSK, QPSK, OQPSK, and MSK are
compared in Figs.
7
and
8.
In Fig.
7,
Gi(x) is shown as a
24-12
REFERENCE
DATA
FOR
ENGINEERS
NORMALIZED
FREQUENCY,
x
Fig.
7.
Power
spectral densities for
PSK
and
MSK.
function of
x
for all three values of i. The parameter
x
can be thought of as normalized frequency, since it is
frequency (in hertz) divided by the data rate
R
(in bits
per second). Note that
x
is therefore a dimensionless
parameter.
Specifications on signal spectra (e.g., bandwidths)
are often given in terms of the power spectral densities
in decibels (dB). Fig.
8
shows
Gi(x)
in decibels
as
a
function of
x.
Since
Gj(x)
is a power density, the
conversion
is
10
log,,[G,(x)]. The 3-dB bandwidth of
Si(f)
is the width of a frequency band outside of which
the power spectral density is at least 3 dB below
S,(f,),
its value at the center of the band. Typically, band-
widths are .normalized by dividing by
R,
which is
equivalent to specifying the bandwidth in terms of the
normalized frequency. Since
10
log10(0.5) is approxi-
mately -3 dB, the 3-dB bandwidth is also termed the
half-power bandwidth. In terms of the function
G,,
the
3-dB, or half-power, bandwidth is the largest value of y
for which Gi(y/2)
=
0.5
G,(O).
Analogous definitions are given for other power-
density levels (e.g., the
IO-,
35-, or 50-dB bandwidths)
in reference 15. The 3-dB bandwidths for the PSK and
MSK
signals are
0.88
for BPSK, 0.44 for QPSK and
OQPSK, and 0.59 for MSK; and the 35-dB bandwidths
are 35.12, 17.56, and 3.24, respectively.* The null-to-
*
Reference
15
+5
Yo
Y
g
-5
c
8
-10
W
m
n
5
z
2
!
c
-15
v1
CT
n.
-20
-
25
0
05
10
15
20
NORMALIZED
FREQUENCY,
x
Fig.
8.
Power
spectral
densities
in
decibels.

DIGITAL COMMUNICATIONS
24-13
null bandwidth
is the smallest value of
y
for which
Gi(y/2)
=
0.
As can be seen in Figs.
7
and
8,
the
null-to-null bandwidths
are
2.0
for BPSK,
1.0
for
QPSK and OQPSK, and
1.5
for MSK. Notice that
although MSK has lower side lobes and smaller 35-dB
bandwidth than QPSK, QPSK has a narrower main lobe
(i.e., smaller null-to-null bandwidth) and a smaller
3-dB bandwidth. These and related issues are discussed
in greater detail in references
15
through
22.
OPTIMUM RECEIVERS FOR
DIGITAL COMMUNICATIONS
Receivers for Binary Baseband
Data Transmission
The general model for a binary baseband data trans-
mission system with an additive Gaussian noise channel
is shown in Fig.
9.
The model of Fig.
9
is employed for
coherent RF communications also, because it is the
low-pass equivalent of a binary RF digital communica-
tions system with an additive Gaussian noise channel
and a coherent receiver. The block diagram for the RF
system is shown in Fig.
10.
The input,
s(t)
=
fisk@)
cos[2?rf,t
+
$1
for the RF channel corresponds to the input
sk(t)
for the
baseband channel.
The principal elements of the channel are a binary
signal set
{so,
sl},
an additive Gaussian noise process
X(t),
a linear filter with impulse response
h(t),
a
sampler, and a threshold device. The binary digit
k
is
sent during the nth time interval by transmitting the
signal
sk(t
-
nT)
for
nT
<
t
<
(n
+
1)T.
For
conveniepce, we consider the first time interval (Le.,
n
=
0)
in all that follows. For this time interval, the
channel output
Y(t)
is the sum of the signal
sk(t)
plus the
noise
X(t).
The channel output is the input to the linear time-
invariant filter. The filter output
Z(t)
is the sum of a
filtered version of the signal, which is denoted by
f&),
and a filtered version of the noise. The signal compo-
nent of the filter output is given by
the
convolution
of the functions
sk
and
h,
which we
The output of the filter is sampled at time
To
to
give
the decision statistic
Z(T,).
Our notational convention is
denote by
fk
=
Sk*h.
to let
so
denote the signal that produces the larger output
at sampling time
To;
that is, we assume
In
the threshold device, the decision statistic
Z(T0)
is
compared with a threshold
z,
and the decision
is
that
so
was transmitted if the statistic Z(To) is greater than the
threshold
z.
If Z(To) is less than
z,
the decision is that
the signal
s,
was transmitted. This system always makes
the correct decision in the absence of noise provided
that the threshold is in the range
The channel noise
X(t)
is a wide-sense stationary
random process with autocorrelation function given by
R,(u)
=
E{X(t)X(t
+
u)}
where
E{Y}
denotes the expected value of a random
variable
Y.
Without loss of generality, the channel noise
process can be assumed to have zero mean (the mean
value can always be absorbed in the signal set). The
autocorrelation function for the noise at the output of
the filter is given by
R(u)
=
R,~(v)~(u
-
V) dv
J:,.
where the function
f
is defined by
f(t)
=
I”
-m
h(v)h(v
+
t)
dv
These two expressions are equivalent to R
=
Rx*f
and
f
=
h*g, respectively, where the function
g
is defined by
g(t)
=
h(-t).
That is,
g
is the time reverse of the
impulse response of the filter. Since
f(t)
=
f(-t),
h(v
+
t)
can be replaced
by
h(v
-
t)
in the definition of
the functionf, but the form given above is usually easier
to evaluate.
Let
P&
denote the probability that an error is made
by the receiver when the signal
Sk(t)
is the input to the
channel. The error probability
Pe,k
can be thought of as
a
conditional probability
of
error
given that
Y(t)
=
sk(t)
+
X(t).
That is, if
Hk
denotes the event that the
signal
sk(t)
is transmitted, the probability
Pe,k
is the
conditional probability of error given
Hk.
When the signal
so(t)
is transmitted, the receiver
makes an error if
Z(T,)
is less than the threshold
z.
Yitl
Fig.
9.
Model
of
binary baseband data transmission system.

24-
14
REFERENCE
DATA
FOR
ENGINEERS
Fig.
10.
Model
of
binary coherent
RF
communication system.
Thus,
Given that
so@)
is the transmitted signal,
Z(To)
is a
Gaussian random variable that has mean
jo(T0)
and
variance
u2
=
~(0).
Consequently,
where the function
Q
is defined by
Q(x)
=
1;
(2,rr)-”’
exp(-y2/2) dy
The function
1
-
Q(x)
is the distribution function of a
zero mean, unit variance, Gaussian random variable.
A
discussion of the function
Q
and its properties can be
found in reference
11.
Similarly, if
s
(t)
is transmitted,
Z(To)
is a Gaussian
random variable with mean
3,(To)
and variance
u2
=
R(O),
and an error occurs if
Z(To)
is greater than the
threshold
z.
Therefore, the error probability
Pe,]
is
Pe,l
=
P[z(~o)
>
ZIH~I
=
Q[{z
-
?1Go)V4
Optimum
Threshold
for
General Gaussian
Noise-The choice of the threshold depends on the
performance measure under consideration. One mea-
sure of performance that is often used is the maximum
of the error probabilities,
Pe,m
=
max{Pe,~,Pe,~}
The minimax criterion for selecting
the
threshold is to
choose the threshold
z
to give the smallest possible
value of
P,,,.
The value of
z
that minimizes
P,,,
is given
bY
zm
=
[~^o(To) +
S*I(TO)I/~
and this
is
referred to as the minimax threshold. Notice
that the minimax threshold depends on the signal set
{SO,
SI},
the impulse response of the filter, and the
sampling time
To.
It is convenient to introduce the signal
sd(t)
=
-
sl(t)}/2
~
FILTER
and lets^&) denote the output of the filter when
sd(t)
is
the input (Le.,
s^,
=
sd*h). If the minimax threshold is
employed, the error probabilities
P,,o
and
Pe,,
are given
by
Pe,o
=
f‘e,~
=
Q[~~(ToY~
Whenever these two probabilities are equal, we denote
the common value by
Pe.
As
an example, consider an antipodal signal set
(discussed earlier in this chapter). Since so(t)
=
-s,(t),
the signal
sd(t)
is given by
sd(t)
=
so(t).
The error
probability for the minimax threshold
is
There are other criteria for selecting the threshold
z,
but they typically require additional information about
the data sequence that is to be transmitted. For instance,
if the data sequence is modeled as a random process
with a known probability distribution, the average
probability
of
error can be employed as a criterion. If
pk
denotes the
a
priori probability that the binary digit
k
is
transmitted, the average probability
of
error
is
Pe,A
=
pe,OPO
+
pe,lPl
The threshold that minimizes
Pe,*
is given by
If the data bits
0
and
1
are equally probable (Le.,
po
=
pl),
the thresholds
zA
and
z,
are the same. Otherwise,
the second term on the right-hand side of the expression
for
zA
is a nonzero term that biases the decision in favor
of
the data bit with the largest a priori probability.
For applications in which unequal costs are associat-
ed with the two types
of
errors and the a priori
probabilities
pi
are known, it may be desirable to select
the threshold to minimize the average cost. This is the
well-known Bayes criterion, which is discussed
in
references
4,
9,
and
10.
The
Matched Filter-A white Gaussian noise
process
X(t)
has spectral density
S,(f)
=
N0/2 for allf.
This is just the Fourier transform of a delta function that
has area
N0/2.
If
the channel noise process has this flat
spectral density, the autocorrelation function of the
noise at the output of the filter is given by
Nu)
=
(N0/2lf(u)

DIGITAL COMMUNICATIONS
24-15
where
f
=
h*g,
the convolution of the impulse response
and its time-reverse. Letting
u
=
0,
we find
u2
=
R(0)
=
No
l(h/12/2
The norm of the function
h
is defined by
Consider first the minimax criterion. The optimum
threshold depends on the filter impulse response
h(t),
and for each choice of the filter impulse response, the
corresponding minimax threshold gives the smallest
possible value of
P,,,.
Let
P,
denote this minimum
value of
P,,,
(recall that
P,
=
Pe,o
'=
P,,,
if the minimax
threshold is used).
The value
of
P,
depends on the impulse response of
the filter. For a system with an
additive white Gaussian
noise channel,
the minimum possible value of
P,
is
achieved by the impulse response
Multiplication of the filter impulse response by a
positive constant
c
does not change the error probability
if the corresponding minimax threshold is used,
so
hM(t)
can be any positive constant multiple of
sd(T0
-
t).
A filter with this impulse response is called a
matched filter.
Given a binary signal set
{so,
si},
let
Ei
denote the
energy in the signal
si,
and define
E,
by
E,
=
[Eo
+
E,]/2
The signal correlation
r'
is the inner product
and
r
=
r'/E,
is the correlation coefficient for the given
signal set. The value of
Iri
is never greater than one;
!
moreover,
r
=
-1
only for antipodal signals, and
r
=
+1
only if
so(t)
=
sl(t).
The norm of signal
sd
is related to the energy by
The matched filter impulse response
hM(t)
=
csd(To
-
t)
has norm
If this filter is employed in the receiver, the minimax
threshold is
z,
=
c(Eo
-
E,)/4,
and the signal
Sd(T0)
is
given by
s^d(TO)
=
llsdll
llhrnll
=
c
llsd112
It follows that the error probability for a receiver with a
matched filter and minimax threshold is
P,
=
Q{[EA(l
-
r)/No]'/2}
This is the smallest error probability that can be
achieved (if a single bit is transmitted) with
binary
baseband data transmission or
binary
coherent RF
communications over an additive white Gaussian noise
channel.
Two important points should be made concerning the
above expression for the minimum error probability.
First, the result does not depend on the sampling time
To.
This is because the matched filter automatically
compensates for the sampling time by incorporating a
delay in its impulse response. As a consequence of this,
the sampling time can be selected for convenience of
implementation. In particular, if the signal set
{so,
s,}
is
time limited
to the interval
[0,
TI,
the matched filter is
causal for any choice of
To
not less than
T.
For such a
signal set, the customary choice for the sampling time is
=
T.
The second point is that the minimum probability of
error depends on the three parameters
E,,
No,
and
r.
The energy
EA
can be increased only by increasing the
power in the received signal, and the noise density can
be decreased only by lowering the noise level in the
receiver. Both of these require increased cost and
complexity in the communication system. However, the
parameter
r
can be decreased by proper signal design.
As
previously mentioned,
r
can be no smaller than
-
1,
and
r
=
-1
if and only if the signals are antipodal.
Antipodal signals have equal energy:
E,
=
Eo
=
E,.
As
a consequence, the subscripts on
E
can be omitted, and
the error probability for antipodal signaling, an additive
white Gaussian noise channel, and a matched-filter
receiver is given by
P,
=
Q{[2E/No]
where
E
is the energy per data bit.
The
Correlation Receiver-The matched-filter re-
ceiver is shown in Fig.
11.
The decision statistic
Z(T0)
for this receiver can be expressed in terms
of
the channel
output
Y(t)
by
Z(T0)
=
JYrn
VTO
-
4
h~
(4
du
The impulse response
of
the matched filter is defined in
terms of the binary signal set
{so,
s
I}
by
h,(t)
=
(SO(T0
-
t)
-
SI
(To
-
t)}/2
In
terms of the signal
the matched filter impulse response is
