Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


23-16
REFERENCE
DATA
FOR ENGINEERS
Fig.
20.
Variation
in
pulse position due to the presence of
noise
or
interference.
(From P. F. Punter,
Modulation, Noise,
and Spectral Analysis,
Fig.
18-27,
@
1965,
McGraw-Hill
Book
CO.)
The (SIN), can be improved by decreasing the pulse rise
rr or correspondingly by widening the transmission
bandwidth. For B
s
UT,
(SIN),
=
$zB2
(C/N)i
ForB
=
1/27,
(SIN),
=
2t,2B2 (CIN)i
As
in the case of FM, the (SIN), ratio cannot be
improved indefinitely by widening the bandwidth, be-
cause the noise power introduced at the receiver increas-
es with bandwidth and eventually becomes comparable
to the signal and "takes over" the system.
A
threshold
level thus also exists just as in the FM case. This
threshold level is usually taken as
A,Iu
=
2, or
(GIN),
=
4
(6
dB).
PULSE-CODE
MODULATION
In
PCM, several pulses are used as a code group to
describe the quantized amplitude of a single sample.
For example, a code group of
n
on-off pulses (binary
code) can represent 2" discrete amplitudes or levels,
including zero level.
In
general, in an
s-ary
PCM
system, the number of quantized amplitude levels the
code group can express (including zero level) is given by
M
=
s"
If
a
stands
for
0
or
1,
the binary notation with
n
digits,
al
,
a2,
.
.
*
,
a,,
represents the number
a,20
+
a221
+
a322
+
. . .
+
a,2"-'
In the ternary number system,
a
stands for the pulse
amplitude
0,
1,
2, and the code group
of
n
digits
represents the number
a13'
+
U23'
f
. . .
f
U,3"-'
Table
1
shows how the
64
numbers from
0
through
63
are represented in binary, quaternary, and octonary
notation.
TABLE 1. ENCODING
INTO
BINARY, QUATERNARY,
AND
OCTONARY NUMBERS*
Decimal
Binary
Quaternary Octonary
No.
No.
No.
No.
0
1
2
3
4
5
6
7
8
9
10
11
12
000000
00000
1
0000
10
00001
1
000
100
000101
0001 10
0001
11
001000
001001
001010
00101 1
001100
000
00
1
002
003
010
011
012
013
020
02
1
022
023
030
00
01
02
03
04
05
06
07
10
11
12
13
14
62 111'110 332
76
63
111111
333
77
*From P.
F.
Panter,
Modulation, Noise, and Spectral
Analysis,
Table
20-1,
0
1965,
McGraw-Hill
Book
Co.,
New
York.
Quantization Noise in a PCM
System
Representing the message signal by certain discrete
allowed levels or steps is called quantizing. It inherently
introduces an initial error in the amplitude of the
samples, giving rise to quantization noise.
Uniform Spacing of
Levels-In this case, the
quantizing interval, or step,
Av
is constant, and the
quantizing noise power is given by
Nq
=
(Av)'/12
assuming that the quantization noise is uniformly dis-
tributed between
k
AvI2. Assuming that the ampli-
tudes of the samples are uniformly distributed, the
signal power recovered from the quantized samples is
S,
=
[(M2
-
1)/12](Av)*
where
M
is the number of discrete levels assigned to the
message signal. The ratio of the signal power to the
quantizing noise power
is
SqINq
=
M2
-
1
s
M2,
M
>>
1
Nonuniform Spacing
of
Levels-Quantization
noise can be reduced by the use of nonuniform spacing
of
levels, to provide smaller steps for weaker signals and
coarser quantization near the peak of large signals.
Quantization noise can be minimized by
an
optimum
level distribution that is a function of the probability
density of the signal. The optimum level spacing
Avk
is
given by
[~(vk)]~'~ Av,
=
kIM,
k
=
constant
ANALOG COMMUNICATIONS
23-17
With optimum level spacing, the total minimum error
power is
where
p(v)
is the probability density of the message
signal, and the nonuniform levels are symmetrically
disposed about zero level in the amplitude range
(-V,
VI.
In practice, nonuniform quantization is realized by
compression, followed by uniform quantization as in
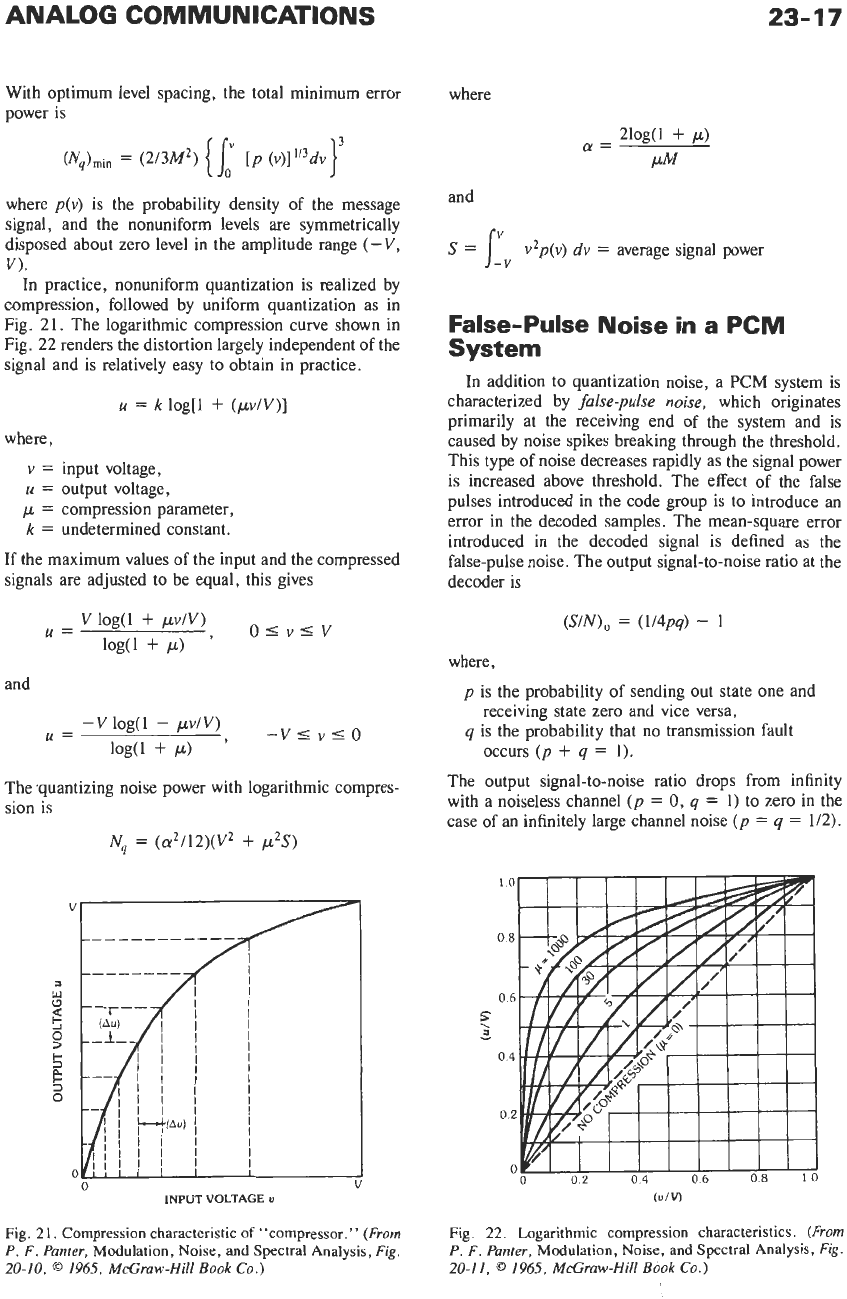
Fig. 21. The logarithmic compression curve shown in
Fig. 22 renders the distortion largely independent of the
signal and
is
relatively easy to obtain in practice.
u
=
k
log[l
+
(pv/V)]
where,
v
=
input voltage,
u
=
output voltage,
p
=
compression parameter,
k
=
undetermined constant.
If the maximum values of the input and the compressed
signals are adjusted
to
be equal, this gives
and
The .quantizing noise power with logarithmic compres-
sion is
Nq
=
(a2/12)(V2
+
p2S)
where
and
s
=
1;”
vzp(v)
dv
=
average signal power
False-Pulse Noise
in
a PCM
System
In addition to quantization noise, a
PCM
system is
characterized by
false-pulse
noise,
which originates
primarily at the receiving end of the system and is
caused by noise spikes breaking through the threshold.
This type
of
noise decreases rapidly as the signal power
is increased above threshold. The effect of the false
pulses introduced in the code group is to introduce an
error in the decoded samples. The mean-square error
introduced in the decoded signal
is
defined as the
false-pulse noise. The output signal-to-noise ratio at the
decoder
is
(SIN),
=
(1/4pq)
-
1
where,
p
is
the probability
of
sending out state one and
q
is the probability that no transmission fault
receiving state zero and vice versa,
occurs
(p
+
q
=
1).
The output signal-to-noise ratio drops from infinity
with a noiseless channel
(p
=
0,
q
=
1) to zero in the
case of an infinitely large channel noise
(p
=
q
=
1/2).
INPUT
VOLTAGE
u
Fig.
2
1.
Compression characteristic
of
“compressor.”
(From
P. F. Punter,
Modulation, Noise, and Spectral Analysis,
Fig.
20-10,
0
1965,
McGraw-Hill
Book
Co.)
Fig.
22.
Logarithmic compression characteristics.
(From
P. F. Punter,
Modulation, Noise, and Spectral Analysis,
Fig.
20-11.
0
1965, McGruw-Hill
Book
Co.)
23-18
REFERENCE DATA
FOR
ENGINEERS
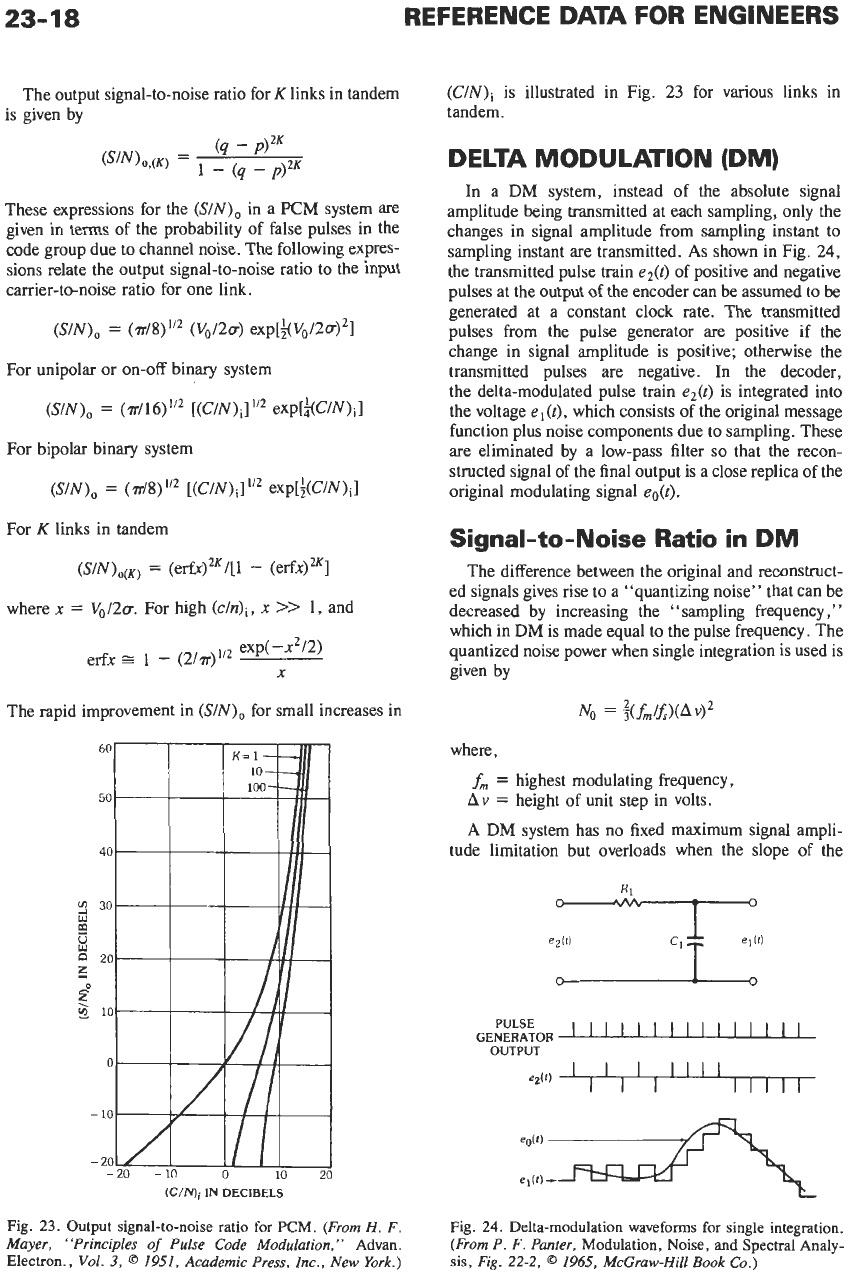
The output signal-to-noise ratio for
K
links in tandem
is given by
These expressions for the
(S/N),
in a
PCM
system are
given in terms of the probability of false pulses in the
code group due to channel noise. The following expres-
sions relate the output signal-to-noise ratio to the input
carrier-to-noise ratio for one link.
(SIN),
=
(3-/8)”’
(V0/2a) e~p[&~/2a)’l
For unipolar or on-off binary system
(SIN),
=
(3-/16)’/*
[(C/N)i]112 e~p[i(C/N)~]
For bipolar binary system
(SIN),
=
(d8)”’
[(GIN),]
e~p[$C/N)~l
For
K
links in tandem
(s/N),(K)
=
(er€xjZK/[I
-
(erf~)~~]
where
x
=
Vo/2a.
For
high
(~/n)~,
x
>>
1,
and
The rapid improvement in
(SIN),
for small increases in
(C/N)i
IN DECIBELS
Fig.
23.
Output signal-to-noise ratio for PCM.
(From H.
F.
Mayer, “Principles
of
Pulse Code Modulation,”
Advan.
Electron.,
Vol.
3,
0
1951,
Academic
Press,
Inc., New
York.)
(C/N)i
is illustrated in Fig.
23
for various links in
tandem.
DELTA MODULATION
(DM)
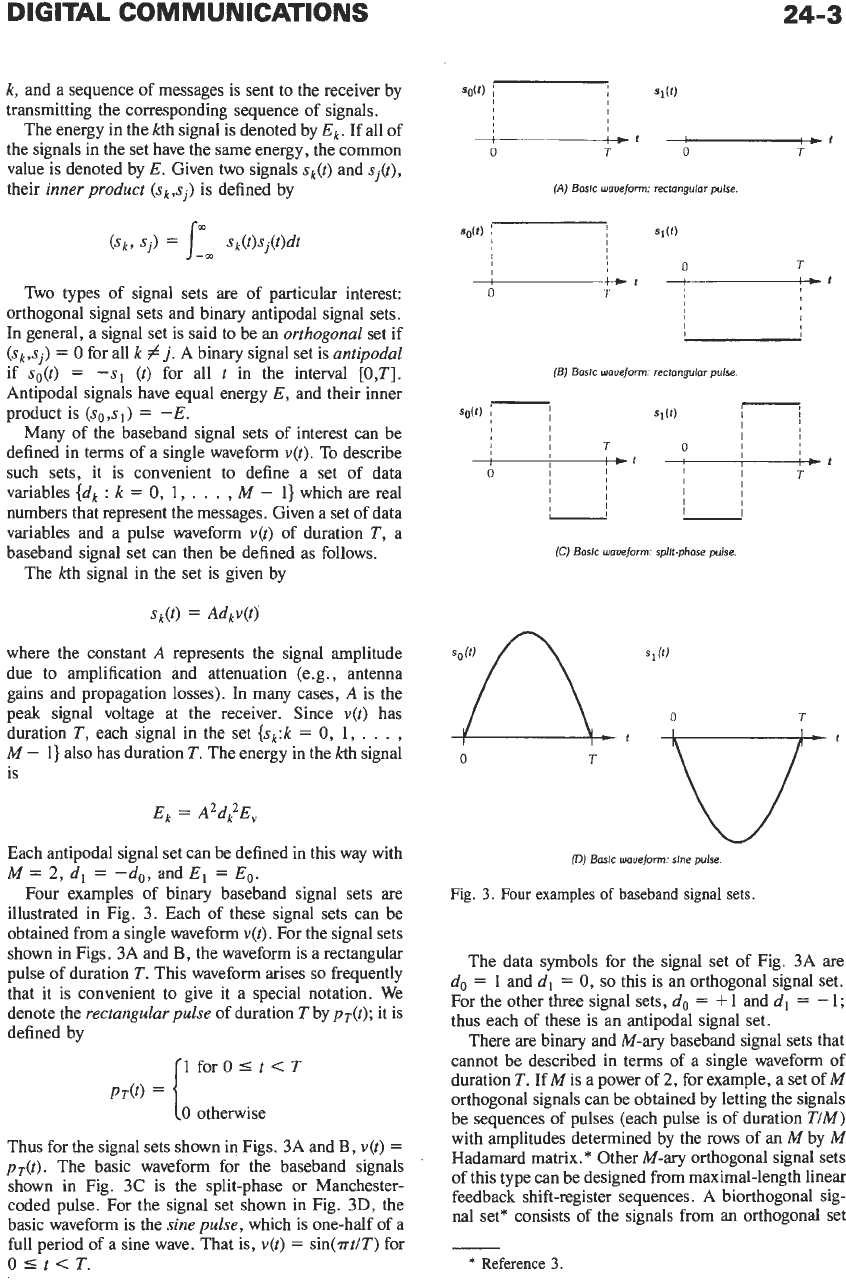
In
a
DM
system, instead of
the
absolute signal
amplitude being transmitted at each sampling, only the
changes in signal amplitude from sampling instant to
sampling instant
are
transmitted.
As
shown in Fig. 24,
the transmitted pulse train
ez(t)
of positive and negative
pulses at the output of the encoder can be assumed to be
generated at a constant clock rate. The transmitted
pulses from the pulse generator
are
positive if the
change
in
signal amplitude is positive; otherwise the
transmitted pulses
are
negative.
In
the decoder,
the delta-modulated pulse train
ez(t)
is
integrated into
the voltage
el@),
which consists of the original message
function plus noise components due to sampling. These
are eliminated by a low-pass filter
so
that the recon-
structed signal of the final output is a close replica of the
original modulating signal
eo@).
Signal-to-Noise Ratio in
DM
The difference between the original and reconstruct-
ed signals gives rise to a “quantizing noise” that can be
decreased by increasing the ‘‘sampling frequency,”
which in
DM
is made equal
to
the pulse frequency. The
quantized noise power when single integration is used is
given by
No
=
%hww2
where,
f,
=
highest modulating frequency,
Av
=
height of unit step in volts.
A
DM
system has no fixed maximum signal ampli-
tude limitation but overloads when the slope of the
PULSE
OUTPUT
GENERATOR
111111111111111
Fig.
24.
Delta-modulation waveforms for single integration.
(From P.
F.
Punter,
Modulation, Noise, and Spectral Analy-
sis,
Fig.
22-2,
0
1965,
McGraw-Hill
Book
Co.)

23-19
signal is too large. The largest slope the system can
reproduce is one that changes
by
one level or step every
pulse interval, so that the maximum signal power
depends on the type of signal. The signal power in the
calculation of signal-to-noise ratio is taken as the power
of the sinusoidal tone.that is just below the overload
point. The maximum amplitude of such
a
sinusoidal
signal
of
frequency fthat can be transmitted with single
integration without overloading is
A
=f,
(Av)/272f
The average signal power is
so
that the signal-to-noise ratio for single integration is
(SIN),,
=
ir3
(f,Inf)*
where
r
=
f,12fm
=
bandwidth expansion factor. The
signal-to-noise ratio for double integration is
(SIN),,
=
ir5
(
fm/7cf)4
Thus, the improvement in signal-to-noise ratio varies
withA3 for the system with single integration, whereas it
varies withA5 for double integration.

24
Digital
Communications
Michael
B.
Pursley
Baseband Signal Sets
24-2
Signal Sets for RF Channels
24-4
Amplitude-Shift Keying (ASK)
Binary Phase-Shift Keying (BPSK)
Quadriphase Shift Keying (QPSK)
Offset Quadriphase Shift Keying (OQPSK)
Minimum-Shift Keying (MSK)
Binary Frequency-Shift Keying (FSK)
Continuous-Phase Frequency-Shift Keying (CPFSK)
M-ary Signaling and Multiple Frequency Shift Keying (MFSK)
Spectra of PSK and MSK Signals
Optimum Receivers for Digital Communications
24-13
Receivers for Binary Baseband Data Transmission
Coherent Receivers for Binary and Quaternary RF Signals
Noncoherent Receivers
Error Probabilities for Digital Communication Systems
24-18
Coherent Systems With Additive White Gaussian Noise Channels
Noncoherent Systems With Additive White Gaussian Noise
Noncoherent Systems With Nonselective Fading Channels
Channels
Spread-Spectrum Communications
24-24
Direct-Sequence Spread-Spectrum Communications
Frequency-Hop Spread-Spectrum Communications
24-
1

24-2
REFERENCE
DATA
FOR
ENGINEERS
SOURCE
+
ENCODER
-----c
MODULATOR
d
CHANNEL
L
DEMODULATOR
---c
L
DECODER
-
DESTINATION
A general model for a digital communication system
is illustrated in the block diagram of Fig.
1.
The source,
encoder, and modulator are part of the transmitter, and
the demodulator, decoder, and destination are in the
receiver. In this chapter, we are primarily concerned
with the
digital data channel,
which consists of the
modulator, channel, and demodulator; the encoder and
decoder are discussed in Chapter
25.
To focus attention
on the digital data channel, consider the model of Fig.
2.
In this model, the source and the encoder
are
combined into a single element called the message
source, and the decoder is absorbed into the destina-
tion.
The information to be conveyed to the destination
consists of a sequence of elements called
messages.
The
message set
is a set of
M
elements that are indexed by
the integers
0,
1,
.
. .
,
M
-
1.
The modulator pro-
duces signals that
are
used to represent these messages
on the channel. During each transmission interval, the
message source produces one of the
M
messages, and
the corresponding waveform is transmitted over the
channel to the receiver.
Rather than attempting to reproduce the transmitted
waveform (as in an analog communication system), the
goal of the demodulator in a digital communication
system is to determine which of the
M
messages was
sent. It accomplishes this by processing the received
signal, which is a distorted, noisy version of the
transmitted signal. The demodulator first produces a
real number or vector called the
decision statistic.
This
statistic is the input
to
a decision device (e.g., a
threshold device), which bases its decision on a prede-
termined strategy referred
to
as a
decision rule.
Deci-
sion rules are selected according to various criteria such
as average probability of error.
The set of allowable decisions can be different from
the message
set,
such as when we permit the receiver to
erase symbols. For example, the binary erasure channel
has a message set {O,l}, but the set of allowable
decisions is
(0,
1,
e},
where
“e”
denotes the erasure.
This is in contrast to the binary “hard-decision”
channel, which has the set
{O,l}
as both the message set
and the set of allowable decisions.
The number of waveforms available to represent the
messages is typically reflected in the names of the
elements associated with the communications system
(including the system itself). For
M
=
2,
the signal sets,
modulation techniques, and communications systems
are referred to as
binary;
for
M
=
3,
they are called
ternary;
and for
M
=
4,
they are called
quaternary.
In
this chapter, the term
M-ary
refers to nonbinary signal-
ing (i.e., it is implicit that
M
>
2).
All of the digital modulation schemes described here
use
time-limited waveforms.
A
waveform
v(t)
is
time
limited
if
v(t)
=
0
for values of
t
outside some finite
interval, and we say it is of
duration
T
if this interval is
[O,T].
The energy
is
perhaps the most important
parameter of the transmitted signal. In general, the
energy
E,
in the waveform
v(t)
is
E,
=
v2(t) dt
If
v(t)
has duration
T,
E,
=
v2(t) dt
BASEBAND SIGNAL SETS
A baseband signal set is a collection of
M
baseband
signals
{sk:k
=
0,
1,
. .
.
,
M
-
1}, each
of
which
is
of
duration
T.
The kth signal
sk(t)
represents the message
1
I
1
I
MESSAGE
’
MODULATOR
-
CHANNEL
-
DEMODULATOR
&
DESTINATION
SOURCE
I
I I
I
I
I
I
I
I I
I
1
I
NOISE
24-3
k,
and a sequence of messages is sent to the receiver by
transmitting the corresponding sequence of signals.
The energy in the kth signal is denoted by
E,.
If all of
the signals in the set have the same energy, the common
value is denoted by
E.
Given two signals
sk(t)
and
si@),
their
inner product
(sk,sj)
is defined by
Two types of signal sets are of particular interest:
orthogonal signal sets and binary antipodal signal sets.
In
general, a signal set is said to be an
orthogonal
set if
(sk,sj)
=
0
for all
k
#
j.
A binary signal set is
antipodal
if
so(t)
=
-sl
(t)
for all
t
in the interval
[O,T].
Antipodal signals have equal energy
E,
and their inner
product is
(so,sI)
=
-E.
Many of the baseband signal sets of interest can be
defined in terms of a single waveform
v(t).
To describe
such sets, it is convenient to define a set of data
variables
{dk
:
k
=
0,
1, .
.
.
,
M
-
1)
which are real
numbers that represent the messages. Given a set of data
variables and a pulse waveform
v(t)
of
duration
T,
a
baseband signal set can then be defined as follows.
The kth signal in the set is given by
~k(t)
=
Adkv(t)
where the constant
A
represents the signal amplitude
due to amplification and attenuation (e.g., antenna
gains and propagation losses).
In
many cases,
A
is the
peak signal voltage at the receiver. Since
v(t)
has
duration
T,
each signal in the set
{Sk:k
=
0,
1,
. .
.
,
M
-
1)
also has duration T. The energy in the kth signal
is
Ek
=
A2d:E,
Each antipodal signal set can be defined in this way with
M
=
2,
d,
=
-do,
and
E,
=
Eo.
Four examples of binary baseband signal sets are
illustrated in Fig. 3. Each of these signal sets can be
obtained
from
a single waveform
v(t).
For the signal sets
shown in Figs. 3A and
B
,
the waveform is a rectangular
pulse of duration
T.
This waveform arises
so
frequently
that it is convenient to give it a special notation. We
denote the
rectangular pulse
of duration
T
by
pT(t);
it is
defined by
1
for
0
5
t
<
T
i
0
otherwise
PT@)
=
Thus for the signal sets shown in Figs. 3A and
B,
v(t)
=
pT(t).
The basic waveform for the baseband signals
shown in Fig.
3C
is the split-phase or Manchester-
coded pulse. For the signal set shown in Fig. 3D, the
basic waveform is the
sine pulse,
which is one-half of a
full period of a sine wave. That is,
v(t)
=
sin(4T) for
OStcT.
I
I
I
--+-----------Ht
tt
0
T
0
T
(A)
Basic waveform: rectangular pulse
(E)
Basfc
waveform: rectangular pulse
I
I
I
I
I
I
I
I
I
I
I
I
(C)
Basic waveform: spllt.phase pulse.
0
7
0
T
(DJ
Basic
waveform: sine pulse.
Fig.
3.
Four
examples of baseband signal sets.
The data symbols for the signal set of Fig. 3A are
do
=
1
and
dl
=
0,
so
this is an orthogonal signal set.
For the other three signal sets,
do
=
+
1
and
d,
=
-
1;
thus each of these is an antipodal signal set.
There are binary and
Mary
baseband signal sets that
cannot be described in terms of a single waveform
of
duration
T.
If
M
is a power of
2,
for example, a set of
M
orthogonal signals can be obtained by letting the signals
be sequences of pulses (each pulse is of duration
TIM)
with amplitudes determined by the rows of an
M
by
M
Hadamard matrix.
*
Other
M-ary
orthogonal signal sets
of this type can be designed from maximal-length linear
feedback shift-register sequences. A biorthogonal sig-
nal set* consists of the signals
from
an orthogonal set
*
Reference
3.

24-4
REFERENCE DATA FOR ENGINEERS
together with all of their negatives. Two signals from a
biorthogonal set are either orthogonal or antipodal.
Of course, the transmitter does not send a single
message; it sends a sequence of messages. In order to
send a sequence of messages, a corresponding sequence
of signals must be transmitted. The message
k
is sent in
the nth time interval by transmitting
sk
during this
interval. The baseband modulation process is described
mathematically as follows. If
m,
denotes the message
produced by the source during the nth interval
[nT,
(n
+
1)T],
the sequence of messages
to
be sent to the receiver
is
(m,)
=
.
. .
,
m-,,
mo, m,,
m2.
.
.
.
If the source output in the nth interval is
k,
m,
=
k
and
the transmitted signal
s(t)
is equal to
sk(t
-
nT)
for
nT
I
t
<
(n
+
1)T.
The signal
s(t)
is actually a
sequence of replicas of the basic waveforms, which
suggests the representation
Because the signals available for use in other intervals
are simply replicas of those for
[O,T],
most of the key
features of a particular baseband modulation technique
can be described and analyzed by considering only the
signal set
{sk:k
=
0,
1,
.
. .
,
M
-
I},
which is defined
on the interval
[O,T].
For signal sets that are derived from a single wave-
form
v(t)
on
[O,T],
the above description can be
simplified by taking advantage of the fact that for such
signal sets
The transmitted signal is defined as follows. First, the
message sequence
(m,)
is represented by the corre-
sponding sequence
(b,)
of data variables; the latter
sequence is defined by
b,
=
dk
if
rn,
=
k.
Next, the
transmitted signal can be written as
m
s(t)
=
Ab,v(t
-
nT)
It follows that the signal set can be described and
analyzed by considering only the waveform
v(t)
and the
set of data variables
{dk:k
=
0,
1,
. .
.
,
M
-
1).
As
an example, consider the waveform
v(t)
=
sin(.rrt/T), which is shown in Fig.
3D.
For binary
communications, the message set is
{OJ}.
In order to
use antipodal signals, we can let
do
=
+
1
and
d,
=
-
1,
so
that a binary
0
is transmitted as a positive sine pulse
and a binary
1
is transmitted as a negative sine pulse.
Message sequences for which
mo
=
0,
ml
=
1,
m2
=
1,
and
m3
=
0
correspond to data sequences with
bo
=
+1,
b,
=
-1,
b2
=
-1, and
b3
=
fl.
Theresulting
signal
s(t)
is shown in Fig.
4.
,=-m
Fig.
4.
Transmitted signal
s(t)
for
the
message
sequence
01
10.
SIGNAL SETS FOR RF
CHANNELS
The most general RF signals that are considered in
this section are
of
the form
s(t)
=
A a(t)
c0s[2~~t
+
S(t)
+
dl
where
a(t)
and
O(t)
are baseband signals of the type
described in the preceding section. The signal
a(t)
represents
amplitude modulation,
and
S(t)
represents
phase modulation.
The variable
A
is a real number that
represents the signal amplitude at the receiver. Physical-
ly, the parameter
A
may be the peak signal voltage, such
as when
la(t)l
=
1.
The variable
4
is the phase
of
the
RF carrier at the time
t
=
0
in the absence of any phase
modulation (i.e.,
S(t)
=
0).
This phase angle may or
may not be known to the receiver.
A
variety of RF signal sets can be obtained by
employing the baseband waveforms of Fig.
3,
or other
elementary waveforms, as amplitude and phase modula-
tion in the formulation given above. The most common
RF signal sets that can be generated in this manner are
described below.
The signal energy values given in the descriptions
that follow are based on the assumption that either
2f,T
is
an integer and both
la(t)l
and
O(t)
are constant on
[O,T]
(in which case the value is exact)
orf,T
>>
1
(in
which case the value is a good approximation). These
conditions imply that the double-frequency component
of the square of the signal is negligible. It is also
assumed that the signals
a(t)
and
O(t)
use baseband
waveforms of duration
T.
For such signals the
energy
per data pulse
is defined as follows. If the kth message
is being sent in the interval
[O,T],
the energy is
For several of the modulation schemes,
O(t)
is equal to a
constant
Ok
for
0
5
t
<
T
if the kth message is sent
during the interval
[O,T].
In this case, the energy is
Because of the assumption concerning
AT,
the energy
does not depend on the value of
Ok.
It does depend on

DIGITAL COMMUNICATIONS
24-5
the energy in the waveform
a@),
so
E,
may depend on
the message
k
that is being sent.
Amplitude-Shift Keying (ASK)
The signal structure for amplitude-shift keying
(ASK) is
s(t)
=
A
a(t)
cos(2?rf,t
+
4)
where
a(t)
is a sequence of baseband pulses whose
amplitudes are modulated to represent the messages.
This type of signaling is also commonly referred to as
digital AM or multiamplitude signaling. The baseband
signal
a(t)
can be written as.
m
~(t)
=
b, v(t
-
nT)
*=
-m
where
b,
=
dk
if the kth message is being sent during
the nth interval. The set {dk:k
=
0,
1,
.
.
.
,
M
-
1)
of
data variables is the set of amplitudes for the sequence
of pulses. The simplest case is binary ASK modulation
with do
=
1
and
d,
=
0;
this is known as
on-off
keying
(OOK).
Another important special case results if
M
=
2,
v(t)
is the rectangular pulse of duration T,
do
=
+1, and
dl
=
-
1.
This is just the amplitude-modulation repre-
sentation for BPSK (see next subsection).
In general, the energy per data pulse for ASK
depends on the message being sent. For the kth mes-
sage, the energy is
Ek
=
(A
dk)' E,/2
where
E,
is the energy in the waveform
v(t),
as defined
at the beginning of this chapter.
A modification of ASK is
quadrature
ASK
(QASK),
which is also known as quadrature AM (QAM). The
QASK signal is of the form
s(t)
=
A
{a,(t)
cos[2@
+
41
+
a2(0
sint2.rlft
+
411
The baseband signals
al(t)
and
a2(t)
are
sequences of
pulses of duration
T,
with amplitudes from the set
'3
=
{dk:k
=
0,
1,
. .
.
,
M
-
1).
The QASK signal
s(t)
can
be written as
s(t)
=
s/(t)
+
SQ(t)
where
s&)
=
A
~0~[2n3',t
+
is
the
in-phase
component of
s(t)
and
s&)
=
A
a,@)
sin[2nfct
t
41
41
is the
quadrature
component. Each of these two compo-
nents of the QASK signal is an ASK signal with pulse
duration
T,.
The simplest, commonly used QASK signal set is
4-QASK in which the set
$2
contains only the two values
+
1
and
-
1.
The in-phase and quadrature signals for
4-QASK are each binary antipodal ASK signals. If
a
(t)
and
a2(t)
are sequences of binary pulses derived from a
single binary source (e.g., odd-numbered bits go to the
in-phase channel and even-numbered bits go to the
quadrature channel), and if the source produces binary
digits at the rate of one bit every T seconds, then
T,
=
2T for 4-QASK. The in-phase and quadrature binary
ASK signals each have a data rate of 1/T, bits per
second,
so
the total data rate for the 4-QASK signal is
2/T,
=
1/T bits per second. A single binary ASK signal
would have to use pulses of duration T
=
TJ2 in order
to provide the same data rate, but such a binary ASK
signal would therefore require twice the bandwidth
of
the 4-QASK signal.
If each of these two signals
a
(t)
and
a2(t)
is allowed
to take on more than two values, higher-order QASK
signal sets are obtained. For example, letting
$2
=
{-3,
-
1,
+
1,
+3}
gives the 16-QASK signal set. The
16-QASK signal set is illustrated in Fig.
5,
where points
in signal space
are
determined by the amplitudes for the
pulses in the in-phase and quadrature components of the
signal. This signal set provides a data rate of 4/T, bits
per second, and
so
a binary ASK signal set requires four
times the bandwidth of 16-QASK in order to provide
the same data rate, Greater bandwidth savings relative
to binary ASK can be achieved by letting
9
be larger,
and this is now a standard approach for such applica-
tions as high-speed modems* for telephone lines. The
application of trellis-coded modulation? has further
improved the performance of such modems.
Binary Phase-Shift Keying
(BPSK)
One of the most commonly used binary signal sets is
obtained by shifting the phase of the RF carrier by
+
rr/2 radians or
-
d2 radians, depending on whether
the data bit is a
0
or a
1.
Binary phase-shift keying can
be viewed as binary phase modulation or binary ampli-
tude modulation; the only requirement is that, during
each signaling interval,
s(t)
is one of two sinusoidal
signals that differ in phase by
T
radians.
Suppose that the binary digit
k
is to be sent during the
nth time interval. Viewed as phase modulation, the
corresponding BPSK signal is
A
COS[27Cf,t dk(d2)
f
41
for
nT
5
t
<
(n
+
l)T
where
Ido
-
dl
1
=
2.
The two
most common choices for dk are
do
=
0
and
dl
=
2 or
*
Reference
19.
?
References
18
and
23
