Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.


142
Лекция 13 (2 часа)
Тема «Развертки поверхностей»
План
1.
Понятия и определения.
2.
Основные свойства развертки поверхностей.
3.
Развертка поверхности многогранника.
13.1. ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
При изготовлении разнообразных изделий из плоского (лис-
тового) материала большое практическое применение имеет по-
строение разверток поверхностей. При изучении разверток лю-
бую поверхность рассматривают как тонкую, гибкую, нерастя-
жимую пленку. Некоторые из представленных таким образом
поверхностей можно путем изгибания совместить с плоскостью.
Поверхность называют развертывающейся, если она может
быть совмещена с
плоскостью без разрывов и склеивания. По-
верхности, которые не могут быть совмещены с плоскостью,
относятся к неразвертывающимся поверхностям.
Плоская фигура, полученная в результате развертывания поверх-
ности, называется разверткой этой поверхности.
В практике возникает необходимость изготовления из лис-
тового материала разверток не только развертывающихся по-
верхностей. Теоретически точно можно выполнить развертки
только гранных поверхностей, торсов, конических и цилиндри-
ческих поверхностей. При развертывании конических и цилин-
дрических поверхностей общего вида в практике их аппрокси-
мируют вписанными гранными поверхностями. В этом случае,
чем больше
граней содержит вписанная поверхность, тем точнее
ее развертка. Построенные таким образом развертки называют
приближенными.
Чтобы построить развертку неразвертывающейся поверхно-
сти, ее условно разделяют на части, которые можно прибли-
женно заменить развертывающимися поверхностями. После
этого строят развертку частей, которые в сумме дают условную
развертку неразвертывающейся поверхности.

143
13.2. ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТКИ
Поверхность и ее развертку следует рассматривать (с пози-
ции теории множеств) как два точечных множества.
Согласно определению развертки между отмеченными двумя
множествами устанавливается взаимнооднозначное соответст-
вие, т. е. каждой точке на поверхности соответствует единст-
венная точка на развертке, и наоборот.
На основании этого можно сформулировать следующие
свойства:
1. Длины двух соответствующих
линий поверхности и ее раз-
вертки равны между собой: | AB
| = | A
0
B
0
|, следствием чего явля-
ется: замкнутая линия на поверхности и соответствующая ей ли-
ния на развертке ограничивают одинаковую площадь: S
Ф
=
.S
0
Ф
2. Угол между линиями на поверхности равен углу между соот-
ветствующими линиями на развертке.
3. Прямой на поверхности соответствует прямая на разверт-
ке (обратное утверждение неверно).
4. Параллельным прямым на поверхности соответствуют па-
раллельные прямые на развертке.
5. Линия, принадлежащая поверхности и соединяющая две ее
точки, которой соответствует на развертке прямая,
называется
геодезической.
13.3. РАЗВЕРТКА ПОВЕРХНОСТЕЙ МНОГОГРАННИКОВ
Разверткой многогранника называется плоская фигура, состав-
ленная из его граней, совмещенных с одной плоскостью.
Существует три способа построения развертки многогранни-
ков:
1)
способ треугольников (триангуляция);
2)
способ нормального сечения;
3)
способ раскатки.
Первый способ применяют для построения развертки пира-
мидальных поверхностей, а второй и третий — для развертки
призматических поверхностей. Рассмотрим каждый из упомяну-
тых способов.
Способ треугольников (триангуляция)
Этот способ предполагает построение граней пирамиды с
помощью треугольников. Любой треугольник строят по трем

144
сторонам, определяя натуральную величину каждой из них. Ес-
ли в основании пирамиды лежит n-угольник, то его разбивают
на n — 2 треугольника, и, выполняя последовательно построе-
ния треугольников, получают в итоге нужный многоугольник.
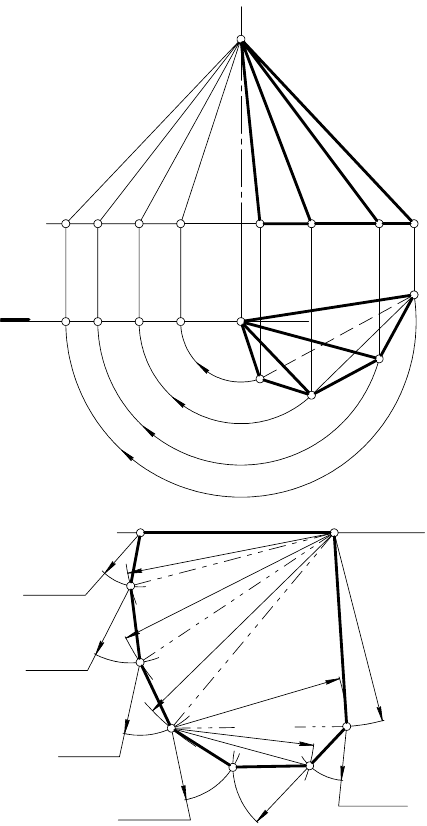
ЗАДАЧА 1. Построить развертку пирамиды SABCD
(рис. 144, а).
РЕШЕНИЕ.
Развертка боковой поверхности пирамиды состоит из тре-
угольников — граней
пирамиды. Основание, четырехугольник
ABCD, разделяют для удобства на два треугольника ABD и BCD.
Длины боковых ребер пирамиды определяют вращением во-
круг оси i ⊃ S и i ⊥ π
1
(рис. 144, а). Каждое ребро вращают до
положения γ
2
плоскости γ ( i ⊂ γ || π
2
). Длины ребер, располо-
женных в основании, проецируются на
π
1
в натуральную вели-
чину. Зная длины всех ребер пирамиды, строят развертку по
следующему плану (рис. 144, б
):
1.
Выбирают произвольно точку S
0
в удобном для построения
развертки месте;
2.
Проводят произвольную прямую l
0
⊃ S
0
;
3.
Откладывают на прямой l
0
[S
0
А
0
] ≅ [
1
2
1
2
S
A
] и строят
U
Α
0
S
0
Β
0
по трем сторонам. Для этого из точки
Α
0
проводят дугу ра-
диусом r
1
= | А
1
В
1
|, а из точки S
0
— дугу радиусом
R
1
= |
1
2
1
2
SB
|. На пересечении дуг определяют вершину
Β
0
треугольника
Α
0
S
0
Β
0
≅
U
Α
S
Β
;
4.
Точки C
0
, D
0
и A
0
определяют, построив треугольники:
U
Β
0
S
0
C
0
≅
U
Β
SC
.
U
C
0
S
0
D
0
≅
U
CSD,
U
D
0
S
0
A
0
≅
U
DSA
по
трем сторонам (построение каждого треугольника анало-
гично построению
U
Α
0
S
0
Β
0
);
5.
К одной из сторон основания на развертке пристраивают
само основание A
0
Β
0
C
0
D
0
пирамиды с помощью треуголь-
ников A
0
D
0
B
0
и D
0
C
0
Β
0
.
На рис. 144, б основание пристроено к стороне A
0
D
0
. Снача-
ла строят вершину B
0
. Из точки D
0
проводят дугу радиусом
r
5
= |D
1
B
1
|, а из точки A
0
— радиусом r
6
= |
А
1
В
1
|. Пересечение дуг
определяет точку B
0
. Аналогично с помощью дуг радиусов
r
7
= |
D
1
C
1
| и r
8
= |B
1
C
1
|, строится точка C
0
.
145
A
2
A
1
B
2
D
2
B
1
C
1
D
1
S
1
≡
i
1
S
2
≡
S
1
2
i
2
C
2
D
1
2
C
1
2
B
1
2
A
1
2
D
1
1
C
1
1
B
1
1
A
1
1
1
2
4
3
g
2
r
1
=
|
A
1
B
1
|
r
2
=
|
B
1
C
1
|
R
4
=
|
A
1
2
S
1
2
|
R
1
=
|
B
1
2
S
1
2
|
R
2
=
|
C
1
2
S
1
2
|
r
4
=
|
A
1
D
1
|
A
0
R
3
=
|
D
1
2
S
1
2
|
r
3
=
|
C
1
D
1
|
B
0
C
0
D
0
A
0
S
0
l
0
1
2
4
3
1
a
б
r
6
=
|
A
1
B
1
|
B
0
r
8
=
|
B
1
C
1
|
C
0
r
7
=
|
C
1
D
1
|
r
5
=
|
D
1
B
1
|
Рис. 144
Соединив точки
Α
0
,
Β
0
, C
0
, D
0
, C
0
,
Β
0
, A
0
, S
0
, A
0
получают
развертку пирамиды SABCD. Линии сгиба на развертке проводят
штрихпунктирной тонкой линией с двумя точками.
146
Способ нормального сечения
Способ нормального
сечения применяют для
построения развертки приз-
матических поверхностей.
Нормальное сечение про-
водят перпендикулярно бо-
ковым ребрам призмы. На
развертке отрезки, равные
сторонам нормального се-
чения, откладывают на
прямой линии. Тогда бо-
ковые ребра на развертке
перпендикулярны этой
прямой линии.
ЗАДАЧА 2. По-
строить развертку тре-
угольной наклонной
призмы ABCA
/
B
/
C
/
(рис. 145).
РЕШЕНИЕ.
1.
Пересекают призму
плоскостью α, перпен-
дикулярной к боковой
поверхности призмы.
2.
Строят сечение (
U
123
)
призмы ABCA
/
B
/
C
/
плоскостью α.
3.
Определяют длины
сторон
U
123. Для это-
го используют способ
вращения вокруг оси
i (1 ∈ i ⊥ π
2
). Плоскость
α (
U
123) вращают до
положения, параллель-
ного π
1
(
1
0
α
f
), тогда [
1
1
1
1
21
]
=
[12
], [
1
1
1
1
32
]=[23
] и [
1
1
1
1
13
]=[31
].
4.
В удобном для построения развертки месте чертежа проводят
горизонтальную прямую a
0
, от произвольной точки кото-
Рис. 145
1
2
4
3
A
0
C
0
B
0
1
0
A
1
B
1
2
1
1
1
1
≡
1
1
1
2
1
3
1
A
2
B
2
C
2
2
2
3
2
B
/
1
C
/
1
A
/
1
C
1
i
1
A
/
2
C
/
2
B
/
2
1
2
≡
1
1
2
≡
i
2
3
1
2
2
1
2
5
7
s
6
8
3
1
1
C
0
A
0
B
/
0
C
/
0
C
/
0
A
/
0
A
/
1
1
0
3
0
2
0
5
7
s
8
6
4
3 1 2
a
0
f
O
a
f
1
O
a
8
s
147
рой 1
0
откладывают последовательно отрезки [1
0
2
0
]
≅
[
1
1
1
1
21 ],
[2
0
3
0
] ≅ [
1
1
1
1
32
] и [3
0
1
0
] ≅ [
1
1
1
1
13
].
5.
Через точки 1
0
, 2
0
, 3
0
и 1
0
проводят прямые, перпендикуляр-
ные прямой a
0
и откладывают на них от точек 1
0
, 2
0
, 3
0
, 1
0
отрезки, конгруэнтные соответствующим длинам боковых
ребер [1A], [1A
/
], [2B], [2B
/
], …, [1A
/
].
6.
Полученные точки соединяют прямыми. Плоская фигура
A
0
B
0
C
0
A
0
/
0
/
0
/
0
/
0
ABCA
A
0
— развертка боковой поверхности приз-
мы.
7.
К развертке боковой поверхности пристраивают к стороне
A
0
B
0
основания призмы —
U
A
0
B
0
C
0
и
U
/
0
/
0
/
0
CBA , предвари-
тельно замерив на развертке истинные размеры сторон
[AC]
≅
[A
0
C
0
], [BС]
≅
[B
0
C
0
].
Способ раскатки
Этот способ применяют в том случае, когда основания
призмы параллельны одной плоскости проекций, а ее боковые
ребра параллельны другой плоскости проекций.
ЗАДАПЧА 3. Построить развертку поверхности наклон-
ной призмы ABCA
/
B
/
C
/
(рис. 146).
РЕШЕНИЕ.
За плоскость развертки принимают плоскость α(α
1
≡ h
0
α
),
проходящую через ребро [AA
/
] и параллельную π
2
. Мысленно
разрезают боковую поверхность призмы по ребру [AA
/
]. Приняв
ребро [AA
/
]
за ось вращения, поворачивают грань AA
/
B
/
B вокруг
него до совмещения с плоскостью α.
При совмещении грани AA
/
B
/
A с плоскостью α ребро
[AA
/
]
≡ [A
0
/
0
A
] не изменит своего положения. Для нахождения
же совмещенного положения ребра [B
0
/
0
B
] из точки B
2
проводят
луч, перпендикулярный к [A
2
/
2
A ], и дугу радиуса |
А
0
В
0
| = |
А
1
В
1
|
из центра A
2
≡ A
0
до взаимного пересечения в точке B
0
. Из точ-
ки B
0
проводят прямую (B
0
/
0
B
) || [A
2
/
2
A
] и откладывают на ней от
точки B
0
отрезок [B
0
/
0
B
] ≅ [A
2
/
2
A
].
Далее принимают совмещенное положение ребра [B
0
/
0
B
] за
новую ось вращения и поворачивают вокруг него грань BB
/
C
/
C
до совмещения с плоскостью α. Для этого из точки C
2
проводят
148
луч, перпендикулярный к совмещенному ребру [B
0
/
0
B
], а из
точки B
0
— дугу окружности радиусом, равным |В
1
C
1
|; пересека-
ясь, дуга и луч определят положение точки C
0
. Через C
0
прово-
дят [C
0
/
0
C
]
|| [B
0
/
0
B
]. Аналогично определяют совмещенное по-
ложение ребра [A
0
/
0
A
]. Соединив построенные точки отрезками
прямых линий, получают развертку боковой поверхности приз-
мы A
2
B
0
C
0
A
0
/
0
A
/
0
C
/
0
B
/
2
A . Пристроив к одному из звеньев лома-
ных A
2
B
0
C
0
A
0
и
/
2
A
/
0
B
/
0
C
/
0
A
треугольники оснований A
0
B
0
C
0
и
/
0
A
/
0
B
/
0
C
, получают фигуру A
0
B
0
A
0
C
0
A
0
/
0
A
/
0
C
/
0
A
/
0
B
/
0
A
A
0
— раз-
вертку призмы ABCA
/
B
/
C
/
.
1
2
3
A
2
≡
A
0
C
2
B
2
B
/
1
C
/
1
A
/
1
B
1
C
1
A
1
B
/
2
C
/
2
A
/
2
≡
A
/
0
B
/
0
A
/
0
C
/
0
A
/
0
A
0
C
0
A
0
B
0
1
2
3
3
1
a
1
≡
h
0
a
Рис. 146
149
Лекция 14 (2 часа)
Тема «Развертки поверхностей»
План
1.
Приближенные развертки поверхностей.
2.
Условные развертки поверхностей.
14.1. ПРИБЛИЖЕННЫЕ РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
Развертка любой развертывающейся поверхности, кроме
гранной, является приближенной. Потеря точности при выпол-
нении графических построений развертки поверхности проис-
ходит потому, что приходится спрямлять или разгибать кривые
линии, принадлежащие поверхности, так как последнюю ап-
проксимируют поверхностями вписанных или описанных мно-
гогранников.
Для построения развертки цилиндрической поверхности ис-
пользуют те же способы нормального
сечения и раскатки, что и
для боковой поверхности призмы. В цилиндрическую поверх-
ность вписывают ( или описывают около нее) призматическую
поверхность и вместо развертки цилиндрической поверхности
выполняют развертку призматической (см. 13.3., задачи 2 и 3).
Развертку конической поверхности строят способом тре-
угольников (см. 13.3., задача 1). При этом коническую поверх-
ность аппроксимируют вписанной в нее пирамидальной
по-
верхностью.
Рассмотрим построение приближенных разверток на приме-
ре цилиндрической поверхностей.
ЗАДАЧА. Построить развертку наклонного эллиптическо-
го цилиндра α с круговым основанием (рис. 147).
РЕШЕНИЕ.
1.
Делят окружность основания цилиндра на n равных час-
тей (на чертеже n = 12).
2.
Вписывают в цилиндр двенадцатиугольную призму, кото-
рой заменяют цилиндрическую поверхность α.
3.
Через ребро призмы 1 проводят плоскость γ
||
π
2
, которую
принимают за плоскость развертки.
150
4.
Строят развертку боковой поверхности цилиндра спосо-
бом раскатки аналогично построению развертки призмы,
выполненному на рис. 146, 13.3.
a
0
a
1
a
2
1
2
≡
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
0
1 0
0
1 1
0
1 2
0
1
0
2
1
1
1
3
1
4
1
5
1
6
1
7
1
8
1
9
1
1 0
1
1 1
1
1 2
1
g
1
≡
h
0
g
7
2
4
2
≡
1 0
2
6
2
≡
8
2
5
2
≡
9
2
3
2
≡
1 1
2
2
2
≡
1 2
2
Рис. 147
14.2. УСЛОВНЫЕ РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
Неразвертываемые поверхности не могут быть совмещены с
плоскостью без разрывов и склеивания, т. е. теоретически не
имеют развертки. Поэтому далее будут рассмотрены способы
построения условных разверток неразвертываемых поверхно-
стей.
В общем случае, при построении развертки неразвертывае-
мой поверхности, отсеки заданной поверхности аппроксимиру-
151
ются отсеками развертывающихся поверхностей — гранными,
цилиндрическими (рис. 148) или коническими (рис. 149).
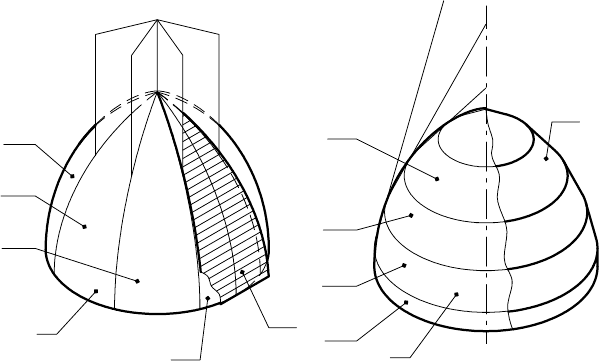
На рис. 148 показана поверхность вращения α, состоящая из
долей α
1
, α
2
, …, α
j
, границами между которыми служат мери-
дианы поверхности α. При построении развертки каждую долю
поверхности α заменяют отсеком цилиндрической поверхно-
сти β
j
. Совокупность отсеков цилиндрических поверхностей
β
1
U β
2
U … β
j
составляют условную развертку поверхности α.
g
1
a
g
2
g
3
g
4
a
1
a
2
a
3
a
j
b
j
a
a
1
a
2
a
3
a
j
b
j
Рис. 148 Рис. 149
Рис. 149 поясняет пример перехода от поверхности враще-
ния α к поверхности β, составленной из отсеков конических
поверхностей β
j
, которыми заменяют части α
1
, α
2
, …, α
j
, поверх-
ности α; границами между этими частями являются параллели
поверхности α (на рис. 149 обозначен только один отсек β
j
).
Пример использования цилиндрической поверхности для
построения условной развертки поверхности α закрытого тора
дан на рис. 150. Построения выполнены в следующем порядке:
1.
Делят горизонтальный очерк поверхности α на n равных
частей (на рис. 150 n = 8).
2.
Рассекают поверхность тора α горизонтально проецирую-
щими плоскостями γ
1
, γ
2
, …, γ
j
проходящими через ось i.
