Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.

152
b
5
b
4
b
3
b
2
a
1
1
b
5
0
b
4
0
b
3
0
b
2
0
b
1
0
a
1
a
2
3
0
2
1
1
1
A
1
a
0
5
0
7
0
S
0
1
0
2
0
4
0
6
0
8
0
A
0
3
1
5
1
7
1
8
1
6
1
4
1
g
1
1
g
2
1
B
1
C
1
D
1
S
0
b
6
0
b
7
0
S
2
i
2
g
3
1
g
4
1
b
1
D
0
C
0
B
0
1
2
≡
2
2
≡
A
2
3
2
≡
4
2
≡
B
2
5
2
≡
6
2
≡
C
2
7
2
≡
8
2
≡
D
2
S
1
≡
i
1
Рис. 150
3.
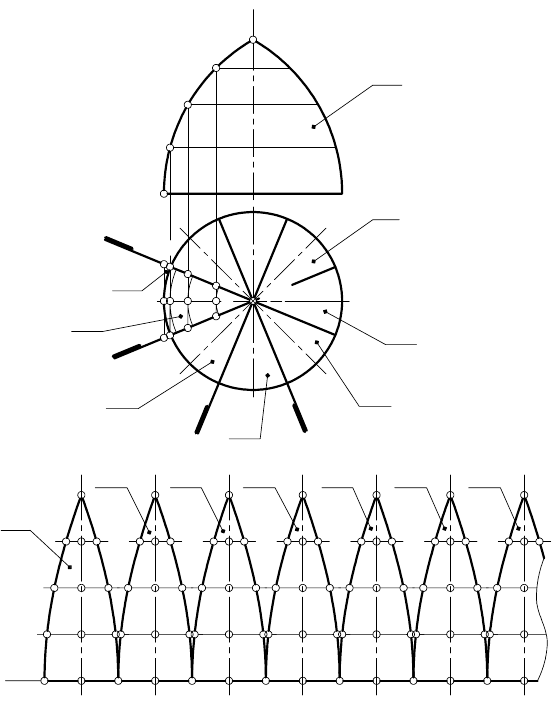
Отсеки поверхности тора α
1
, α
2
, …, заключенные между
меридиональными плоскостями γ
1
и γ
2
, γ
2
и γ
3
, … заменяют
частями цилиндрических поверхностей β
1
, β
2
, …, прямо-
линейные образующие которых 12, 34, 56, 78 перпендику-
лярны к плоскости линий средних меридиональных сече-
ний (например, (12 ) перпендикулярна к плоскости дуги
АS в отсеке α
1
).
4.
На свободном месте чертежа проводят прямую a
0
и на ней
откладывают [1
0
2
0
] ≅ [1
1
2
1
]. Через середину этого отрезка
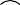
153
проводят вертикальную прямую, на которой откладывают
спрямленное меридиональное сечение дугу АS, отмечая на
ней точки
Α
0
,
Β
0
, C
0
, D
0
и S
0
пересечения меридиональ-
ного сечения с параллелями тора. Через точки проводят
горизонтальные прямые и на них откладывают по обе сто-
роны от прямой А
0
S
0
отрезки, равные половине длин каса-
тельных, проведенных в точках
Α
1
,
Β
1
, C
1
и D
1
к дугам па-
раллелей, заключенных между плоскостями γ
1
и γ
2
. Полу-
ченные точки 1
0
, 3
0
, 5
0
, 7
0
, S
0
и 2
0
, 4
0
, 6
0
, 8
0
, S
0
соединяют
плавными кривыми. Фигура 1
0
S
0
2
0
≅
1
0
β
— условная раз-
вертка одной доли α
1
поверхности тора α.
5.
Чтобы получить условную развертку всей поверхности то-
ра α к доле
1
0
β
необходимо пристроить еще семь фигур
2
0
β
,
3
0
β
,
4
0
β
,
5
0
β
,
6
0
β
,
7
0
β
,
8
0
β
, конгруэнтных фигуре
1
0
β
(на
рис. 150 доля
8
0
β
не показана).

154
Лекция 15 (2 часа)
Тема «Метрические задачи»
План
1.
Понятия и определения.
2.
Определение расстояний.
3.
Определение углов.
15.1. ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Метрические задачи (см. 1.5.) дают возможность по метри-
чески искаженным проекциям судить о форме и размерах ори-
гинала, т. е. определяют способы решения задач по нахождению
неискаженных линейных и угловых величин.
Метрическими называют задачи, решение которых сводится к
нахождению характеристик геометрических фигур, измеряемых
линейными и угловыми величинами.
Все многообразие метрических задач можно разделить на
два вида:
1.
Задачи на определение расстояния между двумя точками.
2.
Задачи на нахождение величины угла между двумя пере-
секающимися прямыми.
В основе решения любой метрической задачи лежит инвари-
антное свойство 2 б ортогонального проецирования (см. 1.5.):
(Ф ⊂
α) ∧ (α
||
π
1
) ⇒ Ф
1
≅
Ф
.
Рассмотрим решение метрических задач обоих видов.
15.2. ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ
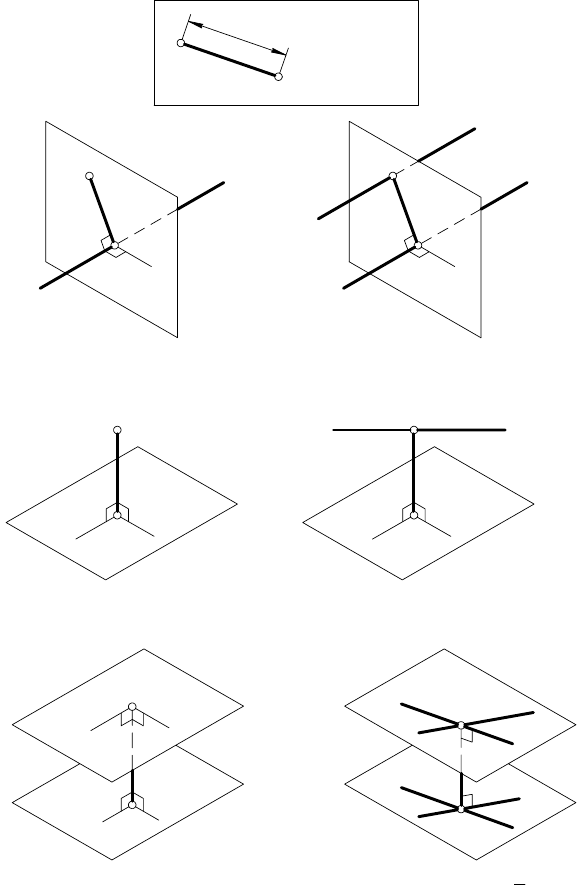
К первому виду можно отнести шесть метрических задач на
определение расстояния между следующими геометрическими
образами:
a) точкой и прямой (рис. 151, а);
б) двумя параллельными прямыми (рис. 151, б
);
в) точкой и плоскостью (рис. 151, в);
г) прямой и плоскостью (рис. 151, г);
155
д) двумя плоскостями (рис. 151, д);
е) двумя скрещивающимися прямыми (рис. 151, е);
d
d
A
B
A
B
g
l
d
A
B
g
l
b
l
m
m
A
d
B
a
A
d
B
a
m
A
d
B
A
d
B
a
a
a
b
b
|
A l
| =
d
|
m l
| =
d
|
A
α
| =
d
|
m
α
| =
d
|
α β
| =
d
|
m l
| =
d
∧
m
•
l
е
г
б а
в
д
|
A B
| =
d
Рис. 151
156
Каждая задача, в конечном счете сводится к определению
расстояния d между двумя точками A и B: d = | AB |.
Определить расстояние между двумя точками на эпюре
можно с помощью прямоугольного треугольника (см. 2.7.) или
одного из способов преобразования ортогональных проекций.
При решении задач на определение расстояния от точки до
прямой (рис. 151, а)
и между двумя параллельными прямыми
(рис. 151, б
) необходимо провести плоскость γ, перпендикуляр-
ную прямой l (см. 4.6.); затем найти точку B пересечения пря-
мой l с плоскостью γ и истинную величину d = | AB |. Т. е. обе
задачи решают по следующему алгоритму:
1.
A ∈ γ ⊥ l ;
2.
γ I l = B ;
3.
A U B = [AB
] ;
4.
| AB |.
Рассмотрим пример решения задачи на эпюре Монжа.
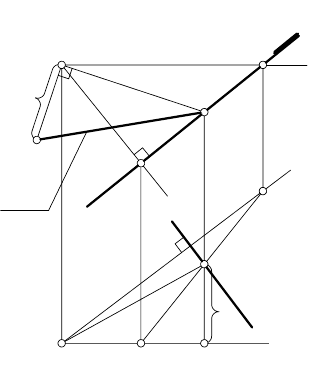
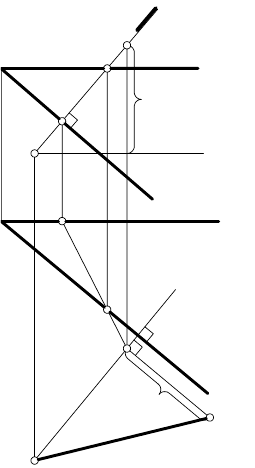
ЗАДАЧА 1. Определить расстояние от точки A до пря-
мой l (рис. 152).
h
2
1
2
B
2
1
1
A
1
C
1
B
1
l
2
≡
a
2
h
1
A
2
A
0
2
1
2
2
l
1
|
A B
|
f
2
f
1
D
y
D
y
Рис. 152
РЕШЕНИЕ.
1.
Через точку A проводят плоскость A ∈ γ
(h
I f )
⊥
l. Тогда h ⊥ l
и f ⊥ l (см. 4.6.). На основании теоремы об ортогональной
проекции прямого угла h
1
⊥ l
1
и f
2
⊥ l
2
(см. 3.2.). Пересе-
157
кающиеся прямые h и f определяют плоскость γ
. Плоскость
γ перпендикулярна прямой l, так как две ее прямые (h I f )
перпендикулярны этой прямой.
2.
Определяем точку пересечения прямой l с плоскостью γ
:
γ I l = B (см. 4.4.). Для этого прямую l заключают во фрон-
тально проецирующую плоскость α
(α
2
≡ l
2
); определяют ли-
нию пересечения (12
) = α I γ
(h I f ) и находят точку
B = l I (12
).
3.
Точку A соединяют с точкой B и образуют отрезок [AB
];
4.
С помощью прямоугольного треугольника A
0
A
2
B
2
находят ис-
тинную величину |
A
0
B
2
| отрезка [AB
] (см. 2.7.). Прямоуголь-
ный треугольник строят по двум катетам [
A
2
B
2
] и [A
0
A
2
]
=
|
B
1
C
1
|
=
∆y. Гипотенуза A
0
B
2
прямоугольного треугольника
равна искомому расстоянию |
AB
| = |
A
l
|.
Чтобы найти расстояние от точки до плоскости (рис. 151, в);
от прямой до параллельной ей плоскости (рис. 151, г); между
двумя параллельными плоскостями (рис. 151, д) и между двумя
скрещивающимися прямыми (рис. 151, е), необходимо из точ-
ки A опустить перпендикуляр l на плоскость α
; найти точку пе-
ресечения B перпендикуляра l с плоскостью α и опреде-
лить |
AB
|.
Все эти задачи решаются также
по одному алгоритму:
1.
A ⊂ l ⊥
α;
2.
l I α =
B
;
3.
|
AB |.
Применение алгоритма рассмот-
рим на примере.
ЗАДАЧА 2. Определить рас-
стояние от точки A до плоскости
α(
h I f ) (рис. 153).
РЕШЕНИЕ.
1.
A ⊂ l ⊥
α
(
h I f ) — через точку A
проводят прямую l ⊥ α
(h I f )
(см. 4.6.). Согласно теореме об
ортогональной проекции прямо-
го угла (см. 3.2.): l
1
⊥ h
1
и l
2
⊥ f
2
,
тогда l (
l
1
, l
2
)
⊥ ⊥ α(
h I f ).
2.
l I
α
(
h
I f )
=
B, т. е. определяют
Рис. 153
h
2
1
2
B
2
1
1
A
1
B
1
h
1
A
2
B
0
2
1
2
2
l
1
f
2
f
1
D
z
D
z
l
2
≡
g
2
≡
f
0
g
|
A
B
|
158
точку B пересечения прямой l с плоскостью α по алгоритму
(см. 4.4.):
а) l ⊂ γ ⊥ π
2
⇒ l
2
≡ γ
2
≡ f
0
γ
;
б) γ I
α (
h
I
f ) = (12
);
в) l I (12
)
=
B
.
3.
Расстояние |
AB
| находят с помощью прямоугольного тре-
угольника A
1
B
1
B
0
, у которого один катет [A
1
B
1
], а другой
[B
1
B
0
] =
∆z. Длина гипотенузы в
U
A
1
B
1
B
0
равна истинной
длине |
AB | = |
Aα
|.
15.3. ОПРЕДЕЛЕНИЕ УГЛОВ
Второй вид метрических задач — определение углов, в ко-
нечном итоге, сводится к нахождению угла между двумя пере-
секающимися прямыми.
Плоский угол проецируется на плоскость проекций без ис-
кажений,
когда
его
стороны
параллельны этой плоскости про-
екций (см. 1.5., свойство 2 б
). Т. е. для определения истинной
величины угла, расположенного в плоскости общего
положения
достаточно плоскость этого угла перевести в положение, парал-
лельное какой-либо плоскости проекций.
Перевести плоскость в положение, удобное для решения за-
дачи, можно с помощью способов преобразования ортогональ-
ных проекций.
Наиболее рациональным способом для решения этой задачи
является способ вращения вокруг линии уровня.
Различают три группы задач по определению углов
между
геометрическими образами:
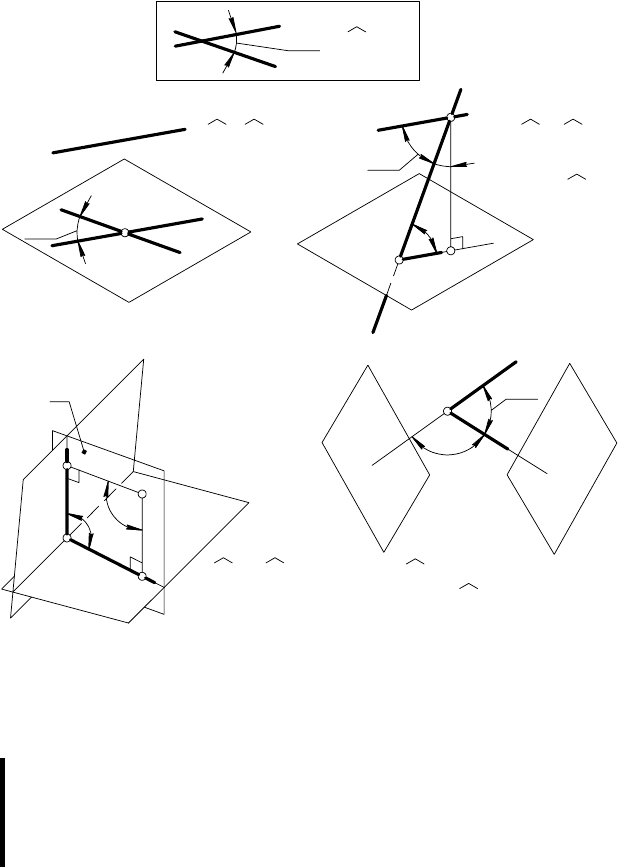
а) двумя скрещивающимися прямыми (рис. 154, а);
б) прямой и плоскостью (рис. 154, б
);
в) двумя плоскостями (рис. 154, в).
159
m
l
f Å
f Å
a
m
A
l
n
f Å
a
C
A
n
l
a
y Å
A
D
C
B
l
n
m
k
f Å
y Å
a
b
y
Å
f Å
a
b
D
p
g
p
k
j Å
B
l
p
l m
=
ϕ °
n l
=
m l
=
ϕ °
m A
∈
l
m | | n
∈
l
α
=
l l
α
=
ϕ
°
ϕ °
= 9 0
° −
ψ
°
ψ °
=
l p
p
⊥ α
а б
г в
α β
=
m n
=
ϕ °
m =
γ
I
α
n =
γ
I
α
α β
=
ϕ °
= 1 8 0
° − ψ °
ψ °
=
k p
k
⊥ α
;
p
⊥ β
Рис. 154
Определение угла между скрещивающимися прямыми
Углом между скрещивающимися прямыми называется плоский
угол, образованный двумя прямыми, проведенными из произволь-
ной точки пространства параллельно данным скрещивающимся
прямым.
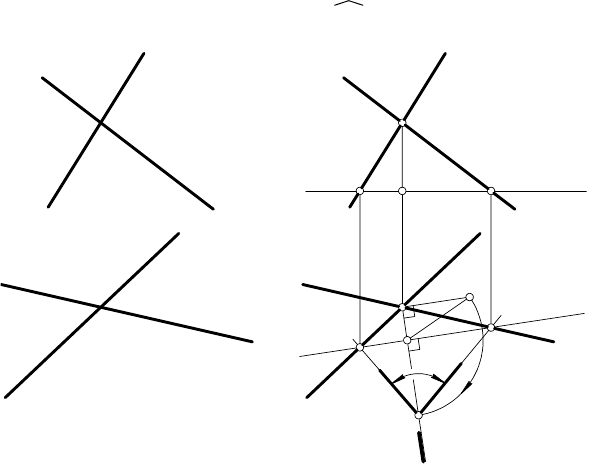
Чтобы определить угол между скрещивающимися прямыми
a и b (рис. 155, а), необходимо выполнить следующие построе-
ния (рис. 155, б
):
1.
Взять произвольную точку A.
160
2.
Провести через точку A прямые a
/
|| a и b
/
|| b.
3.
Определить угол между пересекающимися прямыми
a
/
I b
/
= A способом вращения вокруг горизонтали h,
принадлежащей плоскости угла до положения, парал-
лельного π
1
. Точки 1 и 2 лежат на оси вращения h, по-
этому при вращении они не перемещаются 1 ≡ 1
1
и
2 ≡
2
1
. Для определения нового положения плоскости уг-
ла достаточно осуществить поворот вокруг оси h только
одной точки A (см. 6.3.,). Новое положение
1
1
A
горизон-
тальной проекции точки A совместно с точками
1
1
1
и
1
1
2
определяют искомый угол
1
1
1
1
1
1
2A1
= ϕ°.
h
2
1
1
≡
1
1
1
A
1
h
1
A
2
A
0
2
2
1
2
≡
1
1
2
2
2
≡
2
1
2
2
1
≡
2
1
1
O
2
f
Å
O
1
A
1
1
a
1
a
2
b
2
b
1
a
1
R
a
/
2
b
/
2
b
/
1
a
/
1
а б
Рис. 155
Определение угла между прямой и плоскостью
В элементарной геометрии углом между прямой и плоскостью
называют угол, образованный этой прямой и ее прямоугольной про-
екцией на заданную плоскость.
На рис. 154, б показано построение угла ϕ° между прямой l
и плоскостью α. Угол ϕ° является одним из острых углов пря-
161
моугольного
U
ABC
и равен 90°
—
ψ°
, где ψ° — угол между пря-
мой l и перпендикуляром p ≡ (
BC
), проведенным из любой
точки прямой b к плоскости α.
Для упрощения решения задачи определяют не угол ϕ° = l
α,
а дополняющий его до 90° угол ψ°. В этом случае отпадает не-
обходимость в построении точек A = l I α, C = (BC
) I
α и
проекции l
α
. Определив ψ°, находят ϕ°
= 90°
—
ψ°.
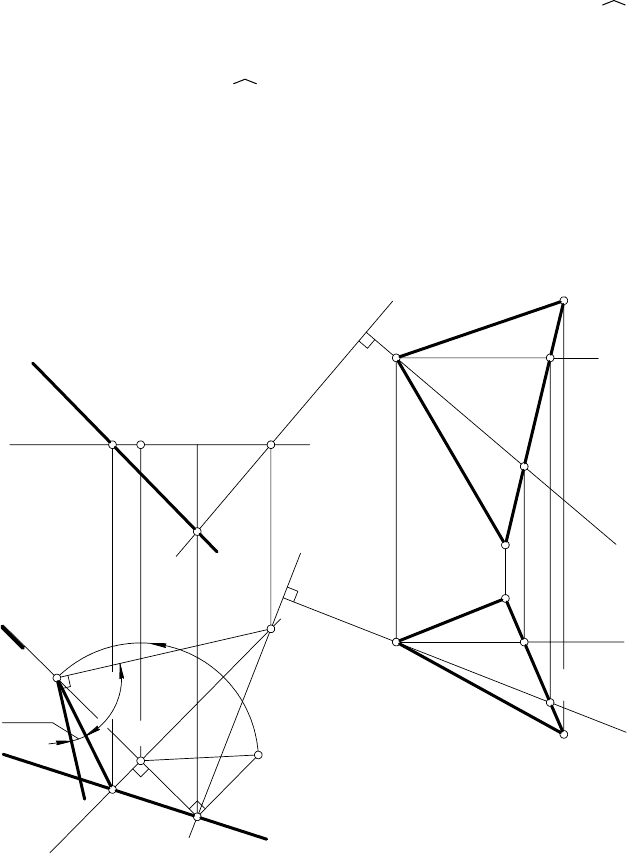
Порядок построения угла между прямой l и плоскостью
U
KLM можно уяснить на примере (см. рис. 156):
1.
B ∈ l
1
— на прямой берут произвольную точку B.
2.
B ∈ p ⊥
α (
U
KLM ) — через точку B проводят перпендикуляр
к плоскости α (
U
KLM ). Для этого, в плоскости проводят
горизонталь h и фронталь f
. Тогда — p
1
⊥
h
1
и p
2
⊥ f
2
.
h
/
2
B
1
h
1
4
1
≡
4
1
1
f
2
O
2
O
1
b
1
l
2
p
2
l
1
p
1
B
0
3
2
≡
3
1
2
4
2
≡
4
1
2
B
2
2
h
2
M
1
h
/
1
y Å
K
1
K
2
M
2
f
1
L
1
L
2
2
1
1
1
1
1
2
1
2
R
B
1
1
3
1
≡
3
1
1
j Å
Рис. 156
