Munson B.R. Fundamentals of Fluid Mechanics

Подождите немного. Документ загружается.

where is the fluid density, and V is the mean velocity in the tube.

Some experimental data obtained with

and are given in the following table:V ⫽ 2 ft

Ⲑ

r ⫽ 2.0 slugs

Ⲑ

,D ⫽ 0.2 ft,

Problems

377

F I G U R E P7.30

0.06 0.08 0.10 0.15

493.8 156.2 64.0 12.6¢p 1lb

Ⲑ

d 1ft2

Δp

Plot the results of these tests, using suitable dimensionless parame-

ters, on log–log graph paper. Use a standard curve-fitting technique

to determine a general equation for . What are the limits of ap-

plicability of the equation?

¢p

mh, mH, m

2.0 0.10 0.833

4.0 0.10 0.833

2.0 0.20 0.417

4.0 0.20 0.417

2.0 0.35 0.238

4.0 0.35 0.238

F I G U R E P7.32

7.33 The time, t, it takes to pour a certain volume of liquid from a

cylindrical container depends on several factors, including the vis-

cosity of the liquid. (See Video V1.3.) Assume that for very viscous

liquids the time it takes to pour out 2/3 of the initial volume depends

on the initial liquid depth, the cylinder diameter, D, the liquid vis-

cosity, and the liquid specific weight, The data shown in theg.m,

following table were obtained in the laboratory. For these tests

and (a) Perform a

dimensional analysis, and based on the data given, determine if vari-

ables used for this problem appear to be correct. Explain how you

arrived at your answer. (b) If possible, determine an equation relating

the pouring time and viscosity for the cylinder and liquids used in

these tests. If it is not possible, indicate what additional information

is needed.

g ⫽ 9.60 kN/m

.D ⫽ 67 mm,/ ⫽ 45 mm,

␮ (N

•

s/m

) 11 17 39 61 107

15 23 53 83 145t1s2

7.34 In order to maintain uniform flight, smaller birds must beat

their wings faster than larger birds. It is suggested that the relation-

ship between the wingbeat frequency, , beats per second, and the

bird’s wingspan, , is given by a power law relationship,

(a) Use dimensional analysis with the assumption that the wingbeat

frequency is a function of the wingspan, the specific weight of the

bird, , the acceleration of gravity, g, and the density of the air, ,

to determine the value of the exponent . (b) Some typical data for

various birds are given in the table below. Does this data support

your result obtained in part (a)? Provide appropriate analysis to

show how you arrived at your conclusion.

v  /

Wingbeat frequency,

Bird Wingspan, m beats/s

purple martin 0.28 5.3

robin 0.36 4.3

mourning dove 0.46 3.2

crow 1.00 2.2

Canada goose 1.50 2.6

great blue heron 1.80 2.0

*7.35 The concentric cylinder device of the type shown in Fig.

P7.35 is commonly used to measure the viscosity, , of liquids by

relating the angle of twist, , of the inner cylinder to the angular ve-

locity, , of the outer cylinder. Assume that

where K depends on the suspending wire properties and has the di-

mensions FL. The following data were obtained in a series of tests

for which , , and and

were constant.D

/ ⫽ 1 ftm ⫽ 0.01 lb ⴢ s

Ⲑ

, K ⫽ 10 lb ⴢ ft

u ⫽ f 1v, m, K, D

, D

, /2

(rad) (rad/s)

0.89 0.30

1.50 0.50

2.51 0.82

3.05 1.05

4.28 1.43

5.52 1.86

6.40 2.14

Determine from these data, with the aid of dimensional analysis,

the relationship between , , and for this particular apparatus.

Hint: Plot the data using appropriate dimensionless parameters,

and determine the equation of the resulting curve using a standard

curve-fitting technique. The equation should satisfy the condition

that for .v ⫽ 0u ⫽ 0

mvu

*7.31 Describe some everyday situations involving fluid flow and

estimate the Reynolds numbers for them. Based on your results, do

you think fluid inertia is important in most typical flow situations?

Explain.

*7.32 As shown in Fig. 2.26, Fig. P7.32, and Video V2.10, a rec-

tangular barge floats in a stable configuration provided the dis-

tance between the center of gravity, CG, of the object (boat and

load) and the center of buoyancy, C, is less than a certain amount,

H. If this distance is greater than H, the boat will tip over. Assume

H is a function of the boat’s width, b, length, and draft, h. (a)

Put this relationship into dimensionless form. (b) The results of a

set of experiments with a model barge with a width of 1.0 m are

shown in the table. Plot these data in dimensionless form and

determine a power-law equation relating the dimensionless para-

meters.

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 377

Section 7.8 Modeling and Similitude

7.36 Obtain a photograph/image of a prototype and the corre-

sponding model that was used for testing. Print these photos and

write a brief paragraph that describes the situation involved.

7.37 Air at is to flow through a 2-ft pipe at an average veloc-

ity of 6 ft s. What size pipe should be used to move water at

and average velocity of 3 ft s if Reynolds number similarity is en-

forced?

7.38 To test the aerodynamics of a new prototype automobile, a

scale model will be tested in a wind tunnel. For dynamic similarity,

it will be required to match Reynolds number between model and

prototype. Assuming that you will be testing a one-tenth-scale

model and both model and prototype will be exposed to standard

air pressure, will it be better for the wind tunnel air to be colder or

hotter than standard sea-level air temperature of ? Why?

7.39 You are to conduct wind tunnel testing of a new football de-

sign that has a smaller lace height than previous designs (see

Videos V6.1 and V6.2). It is known that you will need to maintain

Re and St similarity for the testing. Based on standard college quar-

terbacks, the prototype parameters are set at and

The prototype football has a 7-in. diameter. Due to

instrumentation required to measure pressure and shear stress on

the surface of the football, the model will require a length scale of

2:1 (the model will be larger than the prototype). Determine the re-

quired model freestream velocity and model angular velocity.

7.40 A model of a submarine, 1 : 15 scale, is to be tested at 180 ft

s in a wind tunnel with standard sea-level air, while the prototype

will be operated in seawater. Determine the speed of the prototype

to ensure Reynolds number similarity.

7.41 SAE 30 oil at is pumped through a 3-ft-diameter

pipeline at a rate of A model of this pipeline is to be

designed using a 3-in.-diameter pipe and water at as the work-

ing fluid. To maintain Reynolds number similarity between these

two systems, what fluid velocity will be required in the model?

7.42 The water velocity at a certain point along a 1 : 10 scale

model of a dam spillway is 3 m s. What is the corresponding pro-

totype velocity if the model and prototype operate in accordance

with Froude number similarity?

7.43 The drag characteristics of a torpedo are to be studied in a

water tunnel using a 1 : 5 scale model. The tunnel operates with

freshwater at , whereas the prototype torpedo is to be used in20 °C

Ⲑ

60 °F

6400 gal

Ⲑ

min.

60 °F

Ⲑ

v ⫽ 300 rpm.

V ⫽ 40 mph

15 °C

Ⲑ

60 °F

Ⲑ

80 °F

378 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

F I G U R E P7.35

Liquid

Rotating

outer cylinder

Wire

Fixed support

ᐉ

Inner

cylinder

seawater at To correctly simulate the behavior of the pro-

totype moving with a velocity of 30 m兾s, what velocity is required

in the water tunnel?

7.44 For a certain fluid-flow problem it is known that both the

Froude number and the Weber number are important dimensionless

parameters. If the problem is to be studied by using a 1 : 15 scale

model, determine the required surface tension scale if the density

scale is equal to 1. The model and prototype operate in the same

gravitational field.

7.45 The fluid dynamic characteristics of an airplane flying

240 mph at 10,000 ft are to be investigated with the aid of a 1 : 20

scale model. If the model tests are to be performed in a wind tunnel

using standard air, what is the required air velocity in the wind tun-

nel? Is this a realistic velocity?

7.46 If an airplane travels at a speed of 1120 km兾hr at an altitude

of 15 km, what is the required speed at an altitude of 8 km to satisfy

Mach number similarity? Assume the air properties correspond to

those for the U.S. standard atmosphere.

7.47 (See Fluids in the News article “Modeling parachutes in a wa-

ter tunnel,” Section 7.8.1.) Flow characteristics for a 30-ft-diameter

prototype parachute are to be determined by tests of a 1-ft-diameter

model parachute in a water tunnel. Some data collected with the model

parachute indicate a drag of 17 lb when the water velocity is .

Use the model data to predict the drag on the prototype parachute

falling through air at . Assume the drag to be a function of the

velocity, V, the fluid density, , and the parachute diameter, D.

7.48 The lift and drag developed on a hydrofoil are to be deter-

mined through wind tunnel tests using standard air. If full-scale

tests are to be run, what is the required wind tunnel velocity corre-

sponding to a hydrofoil velocity in seawater at 15 mph? Assume

Reynolds number similarity is required.

7.49 A scale model is to be used in a towing tank to study the

water motion near the bottom of a shallow channel as a large barge

passes over. (See Video V7.16.) Assume that the model is operated

in accordance with the Froude number criteria for dynamic simili-

tude. The prototype barge moves at a typical speed of 15 knots.

(a)At what speed (in ) should the model be towed? (b) Near the

bottom of the model channel a small particle is found to move

0.15 ft in one second so that the fluid velocity at that point is ap-

proximately Determine the velocity at the corresponding

point in the prototype channel.

7.50 A solid sphere having a diameter d and specific weight is

immersed in a liquid having a specific weight and then

released. It is desired to use a model system to determine the max-

imum height, h, above the liquid surface that the sphere will rise

upon release from a depth H. It can be assumed that the important

liquid properties are the density, , specific weight, , and vis-

cosity, . Establish the model design conditions and the prediction

equation, and determine whether the same liquid can be used in

both the model and prototype systems.

7.51 A thin layer of an incompressible fluid flows steadily over a

horizontal smooth plate as shown in Fig. P7.51. The fluid surface is

open to the atmosphere, and an obstruction having a square cross

section is placed on the plate as shown. A model with a length scale

Ⲑ

7 g

0.15 ft/s.

ft/s

1/50

10 ft

Ⲑ

4 ft

Ⲑ

15.6 °C.

F I G U R E P7.51

Free surface

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 378

of and a fluid density scale of 1.0 is to be designed to predict the

depth of fluid, y, along the plate. Assume that inertial, gravitational,

surface tension, and viscous effects are all important. What are the

required viscosity and surface tension scales?

7.52 The drag on a 2-m-diameter satellite dish due to an 80-km hr

wind is to be determined through a wind tunnel test using a geomet-

rically similar 0.4-m-diameter model dish. Assume standard air for

both model and prototype. (a) At what air speed should the model

test be run? (b)With all similarity conditions satisfied, the measured

drag on the model was determined to be 170 N. What is the pre-

dicted drag on the prototype dish?

7.53 A large, rigid, rectangular billboard is supported by an elastic

column as shown in Fig. P7.53. There is concern about the deflec-

tion, , of the top of the structure during a high wind of velocity V.

A wind tunnel test is to be conducted with a 1 : 15 scale model. As-

sume the pertinent column variables are its length and cross-

sectional dimensions, and the modulus of elasticity of the material

used for the column. The only important “wind” variables are the

air density and velocity. (a) Determine the model design conditions

and the prediction equation for the deflection. (b) If the same struc-

tural materials are used for the model and prototype, and the wind

tunnel operates under standard atmospheric conditions, what is the

required wind tunnel velocity to match an 80 km hr wind?

Ⲑ

Problems 379

F I G U R E P7.53

Billboard

Front View

Side View

7.54 A thin flat plate having a diameter of 0.3 ft is towed through

a tank of oil at a velocity of . The plane of the

plate is perpendicular to the direction of motion, and the plate is

submerged so that wave action is negligible. Under these condi-

tions the drag on the plate is 1.4 lb. If viscous effects are neglected,

predict the drag on a geometrically similar, 2-ft-diameter plate that

is towed with a velocity of through water at under con-

ditions similar to those for the smaller plate.

7.55 For a certain model study involving a 1 : 5 scale model it is

known that Froude number similarity must be maintained. The pos-

sibility of cavitation is also to be investigated, and it is assumed that

the cavitation number must be the same for model and prototype.

The prototype fluid is water at and the model fluid is water at

If the prototype operates at an ambient pressure of 101 kPa

1abs2, what is the required ambient pressure for the model system?

7.56 A thin layer of particles rests on the bottom of a horizontal

tube as shown in Fig. P7.56. When an incompressible fluid flows

70 °C.

30 °C,

60 °F3 ft

Ⲑ

5 ft

Ⲑ

s1g ⫽ 53 lb

Ⲑ

through the tube, it is observed that at some critical velocity the par-

ticles will rise and be transported along the tube. A model is to be

used to determine this critical velocity. Assume the critical velocity,

, to be a function of the pipe diameter, D, particle diameter, d, the

fluid density, , and viscosity, , the density of the particles, , and

the acceleration of gravity, g. (a) Determine the similarity require-

ments for the model, and the relationship between the critical

velocity for model and prototype (the prediction equation). (b) For

a length scale of and a fluid density scale of 1.0, what will be the

critical velocity scale (assuming all similarity requirements are

satisfied)?

7.57 The pressure rise, across a blast wave, as shown in Fig.

P7.57 and Video V11.7, is assumed to be a function of the amount

of energy released in the explosion, E, the air density, the speed

of sound, c, and the distance from the blast, d. (a) Put this relation-

ship in dimensionless form. (b) Consider two blasts: the prototype

blast with energy release E and a model blast with the en-

ergy release At what distance from the model blast

will the pressure rise be the same as that at a distance of 1 mile from

the prototype blast?

⫽ 0.001 E2.

1/1000th

¢p,

F I G U R E P7.56

F I G U R E P7.57

Air ( , c)

(2)

Δp = p

– p

(1)

7.58 The drag, on a sphere located in a pipe through which a

fluid is flowing is to be determined experimentally 1see Fig. P7.582.

Assume that the drag is a function of the sphere diameter, d, the

pipe diameter, D, the fluid velocity, V, and the fluid density, (a)

What dimensionless parameters would you use for this problem?

(b) Some experiments using water indicate that for

and the drag is If possible,

estimate the drag on a sphere located in a 2-ft-diameter pipe

through which water is flowing with a velocity of 6 ft兾s. The sphere

diameter is such that geometric similarity is maintained. If it is not

possible, explain why not.

1.5 ⫻ 10

⫺3

lb.V ⫽ 2 ft

Ⲑ

s,D ⫽ 0.5 in.,

d ⫽ 0.2 in.,

F I G U R E P7.58

Sphere

7.59 An incompressible fluid oscillates harmonically (

where V is the velocity) with a frequency of 10 rad s in a

4-in.-diameter pipe. scale model is to be used to determine the

pressure difference per unit length, (at any instant) along the

pipe. Assume that

where D is the pipe diameter, the frequency, t the time, the fluid

viscosity, and the fluid density. (a) Determine the similarity re-

quirements for the model and the prediction equation for . (b) If

the same fluid is used in the model and the prototype, at what fre-

quency should the model operate?

7.60 As shown in Fig. P7.60, a “noisemaker” B is towed behind a

minesweeper A to set off enemy acoustic mines such as at C. The

drag force of the noisemaker is to be studied in a water tunnel at a

⁄4 scale model (model

⁄4 the size of the prototype). The drag force is

¢p

⫽ f 1D, V

, v, t, m, r2

¢p

Ⲑ

sin vt,

V ⫽

JWCL068_ch07_332-382.qxd 9/30/08 8:23 AM Page 379

assumed to be a function of the speed of the ship, the density and

viscosity of the fluid, and the diameter of the noisemaker. (a) If the

prototype towing speed in 3 m s, determine the water velocity in

the tunnel for the model tests. (b) If the model tests of part (a) pro-

duced a model drag of 900 N, determine the drag expected on the

prototype.

Ⲑ

380 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

F I G U R E P7.60

0 2 4 6 8 10 12

Model velocity, ft/s

Model drag,lb

F I G U R E P7.65

7.61 The drag characteristics for a newly designed automobile

having a maximum characteristic length of 20 ft are to be deter-

mined through a model study. The characteristics at both low speed

1approximately 20 mph2and high speed 190 mph2are of interest. For

a series of projected model tests, an unpressurized wind tunnel that

will accommodate a model with a maximum characteristic length

of 4 ft is to be used. Determine the range of air velocities that would

be required for the wind tunnel if Reynolds number similarity is de-

sired. Are the velocities suitable? Explain.

7.62 The drag characteristics of an airplane are to be determined

by model tests in a wind tunnel operated at an absolute pressure of

1300 kPa. If the prototype is to cruise in standard air at 385 km兾hr,

and the corresponding speed of the model is not to differ by more

than 20% from this 1so that compressibility effects may be ignored2,

what range of length scales may be used if Reynolds number simi-

larity is to be maintained? Assume the viscosity of air is unaffected

by pressure, and the temperature of air in the tunnel is equal to the

temperature of the air in which the airplane will fly.

7.63 Wind blowing past a flag causes it to “flutter in the breeze.”

The frequency of this fluttering, is assumed to be a function of

the wind speed, V, the air density, the acceleration of gravity, g,

the length of the flag, and the “area density,” 1with dimensions

of 2of the flag material. It is desired to predict the flutter fre-

quency of a large flag in a wind. To do this a

model flag with is to be tested in a wind tunnel. (a) Deter-

mine the required area density of the model flag material if the large

flag has (b) What wind tunnel velocity is re-

quired for testing the model? (c) If the model flag flutters at 6 Hz,

predict the frequency for the large flag.

†7.64 If a large oil spill occurs from a tanker operating near a

coastline, the time it would take for the oil to reach shore is of

great concern. Design a model system that can be used to investi-

gate this type of problem in the laboratory. Indicate all assump-

tions made in developing the design and discuss any difficulty that

may arise in satisfying the similarity requirements arising from

your model design.

7.65 The drag on a sphere moving in a fluid is known to be a func-

tion of the sphere diameter, the velocity, and the fluid viscosity and

density. Laboratory tests on a 4-in.-diameter sphere were performed

in a water tunnel and some model data are plotted in Fig. P7.65.

For these tests the viscosity of the water was

and the water density was . Estimate the drag on an

8-ft-diameter balloon moving in air at a velocity of . Assume3 ft

Ⲑ

1.94 slugs

Ⲑ

2.3 ⫻ 10

⫺5

Ⲑ

⫽ 0.006 slugs

Ⲑ

/ ⫽ 4 ft

V ⫽ 30 ft

Ⲑ

s/ ⫽ 40 ft

⫺2

Section 7.9 Some Typical Model Studies

7.66 Obtain a photograph/image of a situation where a flow

around an immersed body is being experimentally tested. Print this

photo and write a brief paragraph that describes the situation in-

volved.

7.67 Drag measurements were taken for a sphere, with a diameter

of 5 cm, moving at 4 m s in water at . The resulting drag on

the sphere was 10 N. For a balloon with 1-m diameter rising in air

with standard temperature and pressure, determine (a) the velocity

if Reynolds number similarity is enforced and (b) the drag force if

the drag coefficient (Eq. 7.19) is the dependent pi term.

7.68 A prototype automobile is designed to travel at 65 km hr. A

model of this design is tested in a wind tunnel with identical stan-

dard sea-level air properties at a 1: 5 scale. The measured model

drag is 400 N, enforcing dynamic similarity. Determine (a) the drag

force on the prototype and (b) the power required to overcome this

drag. See Eq. 7.19.

7.69 A new blimp will move at 6 m s in air, and we want to

predict the drag force. Using a 1 : 13-scale model in water at

and measuring a 2500-N drag force on the model, determine (a) the

required water velocity, (b) the drag on the prototype blimp and, (c)

the power that will be required to propel it through the air.

7.70 At a large fish hatchery the fish are reared in open, water-filled

tanks. Each tank is approximately square in shape with curved cor-

ners, and the walls are smooth. To create motion in the tanks, water

is supplied through a pipe at the edge of the tank. The water is

drained from the tank through an opening at the center. (See Video

V7.9.) A model with a length scale of 1  13 is to be used to deter-

mine the velocity, V, at various locations within the tank. Assume

that V ⫽ f (, , , ,g, Q) where is some characteristic length

such as the tank width, represents a series of other pertinent

lengths, such as inlet pipe diameter, fluid depth, etc., is the fluid

density, is the fluid viscosity, g is the acceleration of gravity, and

Q is the discharge through the tank. (a) Determine a suitable set of

dimensionless parameters for this problem and the prediction equa-

tion for the velocity. If water is to be used for the model, can all of

the similarity requirements be satisfied? Explain and support your

answer with the necessary calculations. (b) If the flowrate into the

full-sized tank is 250 gpm, determine the required value for the

model discharge assuming Froude number similarity. What model

depth will correspond to a depth of 32 in. in the full-sized tank?

7.71 Flow patterns that develop as winds blow past a vehicle, such

as a train, are often studied in low-speed environmental (meteoro-

logical) wind tunnels. (See Video V7.16.) Typically, the air veloci-

ties in these tunnels are in the range of to Consider

a cross wind blowing past a train locomotive. Assume that the local

30 m/s.0.1 m/s

/mr/

20 °C

Ⲑ

20 °C

Ⲑ

the air to have a viscosity of and a density of

.2.38 ⫻ 10

⫺3

slugs

Ⲑ

3.7 ⫻ 10

⫺7

Ⲑ

JWCL068_ch07_332-382.qxd 9/30/08 3:39 PM Page 380

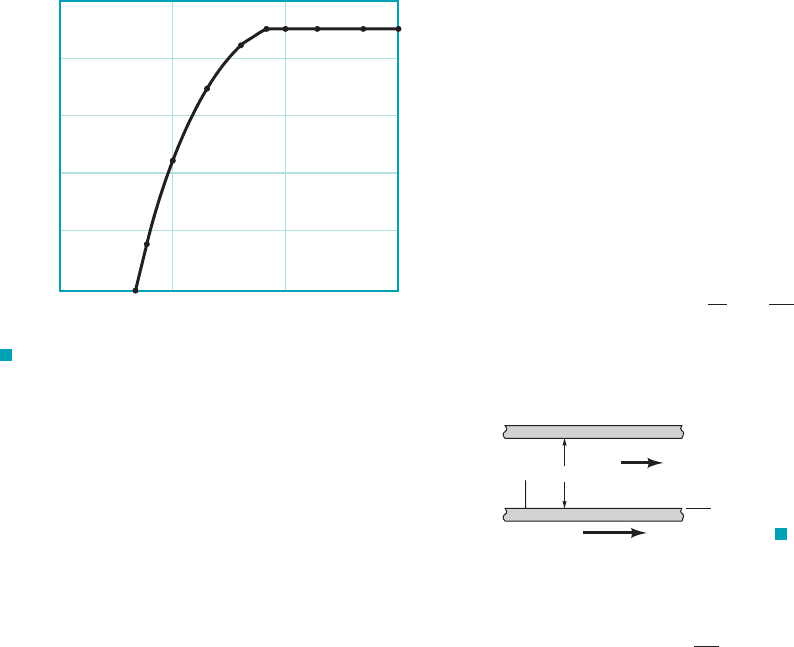
wind velocity, V, is a function of the approaching wind velocity (at

some distance from the locomotive), U, the locomotive length,

height, h, and width, b, the air density, and the air viscosity, (a)

Establish the similarity requirements and prediction equation for a

model to be used in the wind tunnel to study the air velocity, V,

around the locomotive. (b) If the model is to be used for cross winds

gusting to explain why it is not practical to maintain

Reynolds number similarity for a typical length scale 1⬊50.

7.72 (See Fluids in the News article titled “Galloping Gertie,” Sec-

tion 7.8.2.) The Tacoma Narrows bridge failure is a dramatic exam-

ple of the possible serious effects of wind-induced vibrations. As a

fluid flows around a body, vortices may be created which are shed

periodically creating an oscillating force on the body. If the fre-

quency of the shedding vortices coincides with the natural frequency

of the body, large displacements of the body can be induced as was

the case with the Tacoma Narrows bridge. To illustrate this type of

phenomenon, consider fluid flow past a circular cylinder. Assume

the frequency, n, of the shedding vortices behind the cylinder is a

function of the cylinder diameter, D, the fluid velocity, V, and the

fluid kinematic viscosity, . (a) Determine a suitable set of dimen-

sionless variables for this problem. One of the dimensionless vari-

ables should be the Strouhal number, . (b) Some results of ex-

periments in which the shedding frequency of the vortices (in Hz)

was measured, using a particular cylinder and Newtonian, incom-

pressible fluid, are shown in Fig. P7.72. Is this a “universal curve”

that can be used to predict the shedding frequency for any cylinder

placed in any fluid? Explain. (c) A certain structural component in

the form of a 1-in.-diameter, 12-ft-long rod acts as a cantilever beam

with a natural frequency of 19 Hz. Based on the data in Fig. P7.72,

estimate the wind speed that may cause the rod to oscillate at its

natural frequency. Hint: Use a trial and error solution.

Ⲑ

U ⫽ 25 m

Ⲑ

m.r,

Problems

381

0.22

0.20

0.18

0.16

0.14

0.12

10 100 1,000 10,000

Re =VD/v

St=nD/V

F I G U R E P7.72

7.73 (See Fluids in the News article titled “Ice engineering,” Sec-

tion 7.9.3.) A model study is to be developed to determine the force

exerted on bridge piers due to floating chunks of ice in a river. The

piers of interest have square cross sections. Assume that the force,

R, is a function of the pier width, b, the depth of the ice, d, the ve-

locity of the ice, V, the acceleration of gravity, g, the density of the

ice, , and a measure of the strength of the ice, , where has the

dimensions (a) Based on these variables determine a suitable

set of dimensionless variables for this problem. (b) The prototype

conditions of interest include an ice thickness of 12 in. and an ice

velocity of . What model ice thickness and velocity would be

required if the length scale is to be 1 10? (c) If the model and pro-

totype ice have the same density, can the model ice have the same

strength properties as that of the prototype ice? Explain.

Ⲑ

6 ft

Ⲑ

⫺2

7.74 As illustrated in Video V7.9, models are commonly used to

study the dispersion of a gaseous pollutant from an exhaust stack

located near a building complex. Similarity requirements for the pol-

lutant source involve the following independent variables: the stack

gas speed, V, the wind speed, U, the density of the atmospheric air,

the difference in densities between the air and the stack gas,

the acceleration of gravity, g, the kinematic viscosity of the

stack gas, and the stack diameter, D. (a) Based on these variables,

determine a suitable set of similarity requirements for modeling the

pollutant source. (b) For this type of model a typical length scale

might be 1⬊200. If the same fluids were used in model and proto-

type, would the similarity requirements be satisfied? Explain and

support your answer with the necessary calculations.

7.75 River models are used to study many different types of flow

situations. (See, for example, Video V7.12.) A certain small river

has an average width and depth of 60 ft and 4 ft, respectively, and

carries water at a flowrate of A model is to be designed

based on Froude number similarity so that the discharge scale is

1兾250. At what depth and flowrate would the model operate?

7.76 As winds blow past buildings, complex flow patterns can de-

velop due to various factors such as flow separation and interactions

between adjacent buildings. (See Video V7.13.) Assume that the lo-

cal gage pressure, p, at a particular loaction on a building is a func-

tion of the air density, the wind speed, V, some characteristic

length, and all other pertinent lengths, needed to characterize

the geometry of the building or building complex. (a) Determine a

suitable set of dimensionless parameters that can be used to study

the pressure distribution. (b) An eight-story building that is 100 ft

tall is to be modeled in a wind tunnel. If a length scale of 1⬊300 is to

be used, how tall should the model building be? (c) How will a mea-

sured pressure in the model be related to the corresponding proto-

type pressure? Assume the same air density in model and prototype.

Based on the assumed variables, does the model wind speed have to

be equal to the prototype wind speed? Explain.

Section 7.10 Similitude Based on Governing

Differential Equations

7.77 Start with the two-dimensional continuity equation and the

Navier–Stokes equations 1Eqs. 7.28, 7.29, and 7.302and verify the

nondimensional forms of these equations 1Eqs. 7.31, 7.34, and 7.352.

7.78 A viscous fluid is contained between wide, parallel plates

spaced a distance h apart as shown in Fig. P7.78. The upper plate is

fixed, and the bottom plate oscillates harmonically with a velocity

amplitude U and frequency The differential equation for the

velocity distribution between the plates is

where u is the velocity, t is time, and and are fluid density and

viscosity, respectively. Rewrite this equation in a suitable nondi-

mensional form using h, U, and as reference parameters.v

⫽ m

,/,

700 ft

/s.

r ⫺ r

F I G U R E P7.78

= Ucos t

Fixed plate

7.79 The deflection of the cantilever beam of Fig. P7.79 is gov-

erned by the differential equation

⫽ P1x ⫺ / 2

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 381

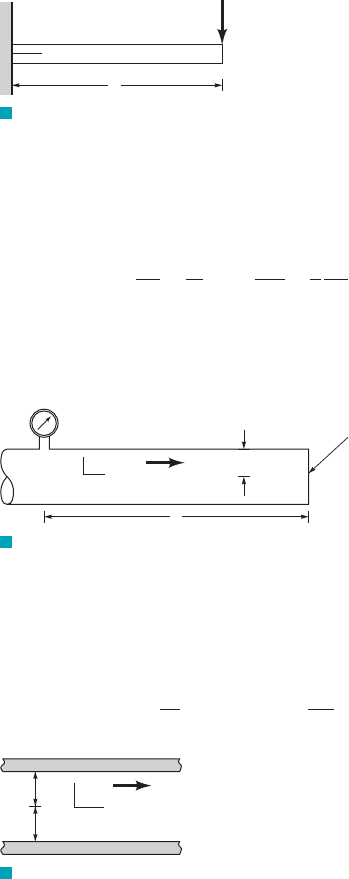
where E is the modulus of elasticity and I is the moment of inertia

of the beam cross section. The boundary conditions are at

and at (a) Rewrite the equation and

boundary conditions in dimensionless form using the beam length,

as the reference length. (b) Based on the results of part 1a2, what

are the similarity requirements and the prediction equation for a

model to predict deflections?

x ⫽ 0.dy

Ⲑ

dx ⫽ 0x ⫽ 0

y ⫽ 0

382 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

F I G U R E P7.80

ᐉ

F I G U R E P7.79

End initially

closed

ᐉ

F I G U R E P7.81

7.81 An incompressible fluid is contained between two infinite

parallel plates as illustrated in Fig. P7.81. Under the influence of a

harmonically varying pressure gradient in the x direction, the fluid

oscillates harmonically with a frequency The differential equa-

tion describing the fluid motion is

⫽ X cos vt ⫹ m

where X is the amplitude of the pressure gradient. Express this

equation in nondimensional form using h and as reference para-

meters.

■ Lab Problems

7.82 This problem involves the time that it takes water to drain

from two geometrically similar tanks. To proceed with this problem,

go to the book’s web site, www.wiley.com/college/munson.

7.83 This problem involves determining the frequency of vortex

shedding from a circular cylinder as water flows past it. To proceed

with this problem, go to the book’s web site, www.wiley.com/

college/munson.

7.84 This problem involves the determination of the head loss for

flow through a valve. To proceed with this problem, go to the

book’s web site, www.wiley.com/college/munson.

7.85 This problem involves the calibration of a rotameter. To pro-

ceed with this problem, go to the book’s web site, www.wiley.com/

college/munson.

■ Life Long Learning Problems

7.86 Microfluidics is the study of fluid flow in fabricated devices

at the micro scale. Advances in microfluidics have enhanced the

ability of scientists and engineers to perform laboratory experi-

ments using miniaturized devices known as a “lab-on-a-chip.” Ob-

tain information about a lab-on-a-chip device that is available com-

mercially and investigate its capabilities. Summarize your findings

in a brief report.

7.87 For some types of aerodynamic wind tunnel testing, it is dif-

ficult to simultaneously match both the Reynolds number and

Mach number between model and prototype. Engineers have de-

veloped several potential solutions to the problem including pres-

surized wind tunnels and lowering the temperature of the flow.

Obtain information about cryogenic wind tunnels and explain the

advantages and disadvantages. Summarize your findings in a brief

report.

■ FlowLab Problems

*7.88 This FlowLab problem involves investigation of the

Reynolds number significance in fluid dynamics through the sim-

ulation of flow past a cylinder. To proceed with this problem, go to

the book’s web site, www.wiley.com/college/munson.

■ FE Exam Problems

Sample FE (Fundamental of Engineering) exam questions for fluid

mechanics are provided on the book’s web site, www.wiley.com/

college/munson.

7.80 A liquid is contained in a pipe that is closed at one end as

shown in Fig. P7.80. Initially the liquid is at rest, but if the end is

suddenly opened the liquid starts to move. Assume the pressure

remains constant. The differential equation that describes the re-

sulting motion of the liquid is

where is the velocity at any radial location, r, and t is time. Rewrite

this equation in dimensionless form using the liquid density, the

viscosity, and the pipe radius, R, as reference parameters.m,

⫽

⫹ m a

⫹

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 382

383

CHAPTER OPENING PHOTO: Turbulent jet: The jet of water from the pipe is turbulent. The complex, irregular,

unsteady structure typical of turbulent flows is apparent. (Laser-induced fluorescence of dye in water.) (Pho-

tography by P. E. Dimotakis, R. C. Lye, and D. Z. Papantoniou.)

Learning Objectives

After completing this chapter, you should be able to:

■ identify and understand various characteristics of the flow in pipes.

■ discuss the main properties of laminar and turbulent pipe flow and appreciate

their differences.

■ calculate losses in straight portions of pipes as well as those in various

pipe system components.

■ apply appropriate equations and principles to analyze a variety of pipe

flow situations.

■ predict the flowrate in a pipe by use of common flowmeters.

In the previous chapters we have considered a variety of topics concerning the motion of fluids.

The basic governing principles concerning mass, momentum, and energy were developed and ap-

plied, in conjunction with rather severe assumptions, to numerous flow situations. In this chapter

we will apply the basic principles to a specific, important topic—the incompressible flow of vis-

cous fluids in pipes and ducts.

The transport of a fluid 1liquid or gas2in a closed conduit 1commonly called a pipe if it is of

round cross section or a duct if it is not round2is extremely important in our daily operations. A brief

consideration of the world around us will indicate that there is a wide variety of applications of pipe

flow. Such applications range from the large, man-made Alaskan pipeline that carries crude oil al-

most 800 miles across Alaska, to the more complex 1and certainly not less useful2natural systems of

“pipes” that carry blood throughout our body and air into and out of our lungs. Other examples

iscous Flow

in Pipes

iscous Flow

in Pipes

Pipe flow is very

important in our

daily operations.

V8.1 Turbulent jet

JWCL068_ch08_383-460.qxd 9/23/08 10:50 AM Page 383

include the water pipes in our homes and the distribution system that delivers the water from the

city well to the house. Numerous hoses and pipes carry hydraulic fluid or other fluids to various

components of vehicles and machines. The air quality within our buildings is maintained at com-

fortable levels by the distribution of conditioned 1heated, cooled, humidified兾dehumidified2air

through a maze of pipes and ducts. Although all of these systems are different, the fluid mechan-

ics principles governing the fluid motions are common. The purpose of this chapter is to under-

stand the basic processes involved in such flows.

Some of the basic components of a typical pipe system are shown in Fig. 8.1. They include

the pipes themselves 1perhaps of more than one diameter2, the various fittings used to connect the

individual pipes to form the desired system, the flowrate control devices 1valves2, and the pumps

or turbines that add energy to or remove energy from the fluid. Even the most simple pipe systems

are actually quite complex when they are viewed in terms of rigorous analytical considerations.

We will use an “exact” analysis of the simplest pipe flow topics 1such as laminar flow in long,

straight, constant diameter pipes2and dimensional analysis considerations combined with experi-

mental results for the other pipe flow topics. Such an approach is not unusual in fluid mechanics

investigations. When “real-world” effects are important 1such as viscous effects in pipe flows2, it

is often difficult or “impossible” to use only theoretical methods to obtain the desired results. A

judicious combination of experimental data with theoretical considerations and dimensional analy-

sis often provides the desired results. The flow in pipes discussed in this chapter is an example of

such an analysis.

384 Chapter 8 ■ Viscous Flow in Pipes

F I G U R E 8.1 Typical pipe system components.

Pump

Tee

Valve

Outlet

Elbow

Inlet

Pipe

Before we apply the various governing equations to pipe flow examples, we will discuss some of

the basic concepts of pipe flow. With these ground rules established we can then proceed to for-

mulate and solve various important flow problems.

Although not all conduits used to transport fluid from one location to another are round in

cross section, most of the common ones are. These include typical water pipes, hydraulic hoses, and

other conduits that are designed to withstand a considerable pressure difference across their walls

without undue distortion of their shape. Typical conduits of noncircular cross section include heat-

ing and air conditioning ducts that are often of rectangular cross section. Normally the pressure dif-

ference between the inside and outside of these ducts is relatively small. Most of the basic princi-

ples involved are independent of the cross-sectional shape, although the details of the flow may be

dependent on it. Unless otherwise specified, we will assume that the conduit is round, although we

will show how to account for other shapes.

8.1 General Characteristics of Pipe Flow

The pipe is as-

sumed to be com-

pletely full of the

flowing fluid.

JWCL068_ch08_383-460.qxd 9/23/08 10:50 AM Page 384

For all flows involved in this chapter, we assume that the pipe is completely filled with the

fluid being transported as is shown in Fig. 8.2a. Thus, we will not consider a concrete pipe through

which rainwater flows without completely filling the pipe, as is shown in Fig. 8.2b. Such flows,

called open-channel flow, are treated in Chapter 10. The difference between open-channel flow and

the pipe flow of this chapter is in the fundamental mechanism that drives the flow. For open-chan-

nel flow, gravity alone is the driving force—the water flows down a hill. For pipe flow, gravity

may be important 1the pipe need not be horizontal2, but the main driving force is likely to be a

pressure gradient along the pipe. If the pipe is not full, it is not possible to maintain this pressure

difference,

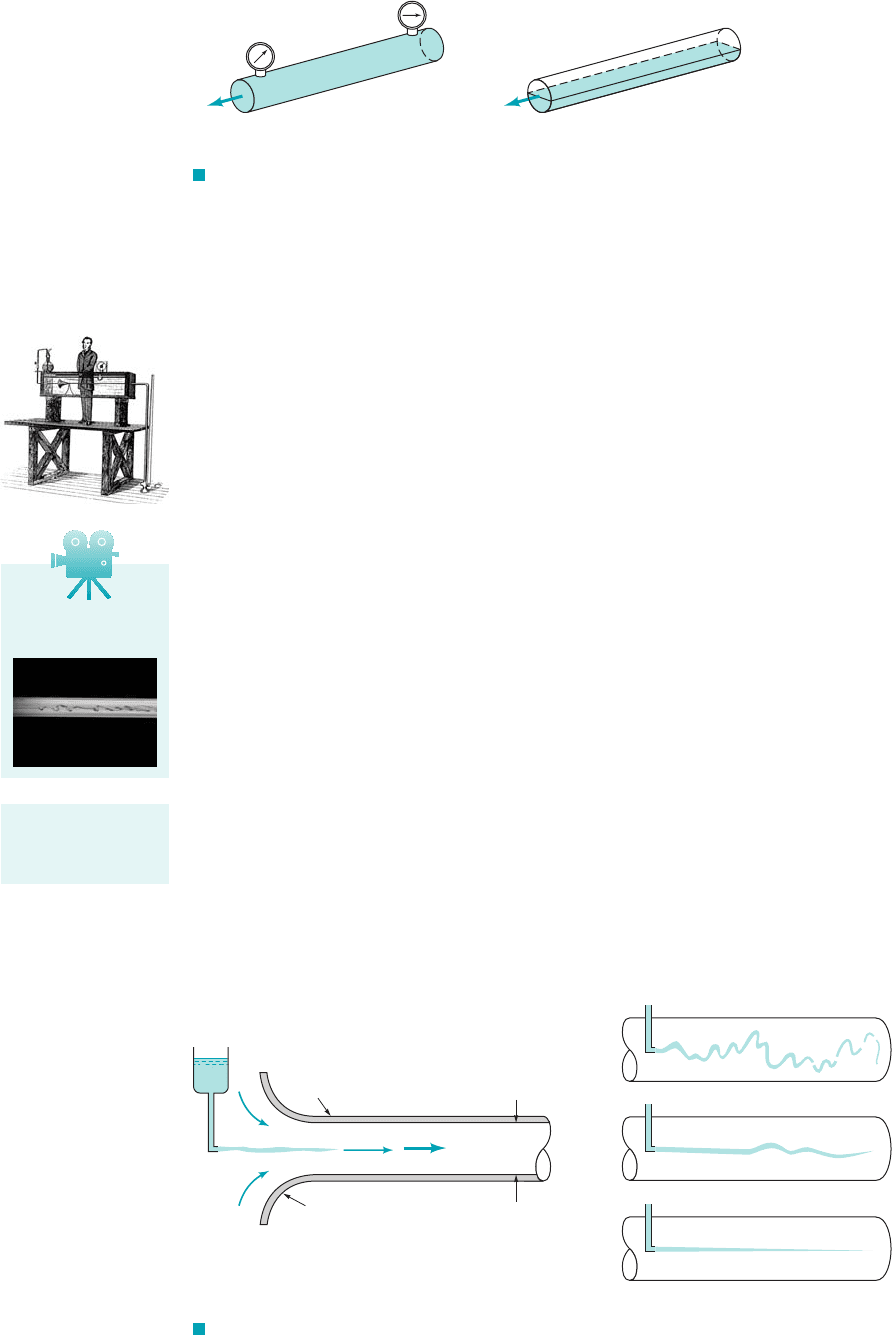
8.1.1 Laminar or Turbulent Flow

The flow of a fluid in a pipe may be laminar flow or it may be turbulent flow. Osborne Reynolds

11842–19122, a British scientist and mathematician, was the first to distinguish the difference be-

tween these two classifications of flow by using a simple apparatus as shown by the figure in the

margin, which is a sketch of Reynolds’ dye experiment. Reynolds injected dye into a pipe in which

water flowed due to gravity. The entrance region of the pipe is depicted in Fig. 8.3a. If water runs

through a pipe of diameter D with an average velocity V, the following characteristics are ob-

served by injecting neutrally buoyant dye as shown. For “small enough flowrates” the dye streak

1a streakline2will remain as a well-defined line as it flows along, with only slight blurring due to

molecular diffusion of the dye into the surrounding water. For a somewhat larger “intermediate

flowrate” the dye streak fluctuates in time and space, and intermittent bursts of irregular behav-

ior appear along the streak. On the other hand, for “large enough flowrates” the dye streak al-

most immediately becomes blurred and spreads across the entire pipe in a random fashion. These

three characteristics, denoted as laminar, transitional, and turbulent flow, respectively, are illus-

trated in Fig. 8.3b.

The curves shown in Fig. 8.4 represent the x component of the velocity as a function of

time at a point A in the flow. The random fluctuations of the turbulent flow 1with the associated

particle mixing2are what disperse the dye throughout the pipe and cause the blurred appearance

illustrated in Fig. 8.3b. For laminar flow in a pipe there is only one component of velocity,

⫺ p

8.1 General Characteristics of Pipe Flow 385

V8.2 Laminar/

turbulent pipe flow

A flow may be lam-

inar, transitional,

or turbulent.

(2)

(

a)(b)

(1)

(2)

(1)

≠ p

= p

F I G U R E 8.2 (a) Pipe flow. (b) Open-channel flow.

Q = VA

Dye streak

Dye

Smooth, well-rounded

entrance

Pipe

(

a)(b)

Laminar

Transitional

Turbulent

F I G U R E 8.3 (a) Experiment to illustrate type of flow. (b) Typical dye streaks.

JWCL068_ch08_383-460.qxd 9/23/08 10:50 AM Page 385

For turbulent flow the predominant component of velocity is also along the pipe, but it

is unsteady 1random2and accompanied by random components normal to the pipe axis,

Such motion in a typical flow occurs too fast for our eyes to follow. Slow

motion pictures of the flow can more clearly reveal the irregular, random, turbulent nature of the

flow.

As was discussed in Chapter 7, we should not label dimensional quantities as being “large”

or “small,” such as “small enough flowrates” in the preceding paragraphs. Rather, the appropriate

dimensionless quantity should be identified and the “small” or “large” character attached to it. A

quantity is “large” or “small” only relative to a reference quantity. The ratio of those quantities re-

sults in a dimensionless quantity. For pipe flow the most important dimensionless parameter is the

Reynolds number, Re—the ratio of the inertia to viscous effects in the flow. Hence, in the previ-

ous paragraph the term flowrate should be replaced by Reynolds number, where V

is the average velocity in the pipe. That is, the flow in a pipe is laminar, transitional, or turbulent

provided the Reynolds number is “small enough,” “intermediate,” or “large enough.” It is not only

the fluid velocity that determines the character of the flow—its density, viscosity, and the pipe size

are of equal importance. These parameters combine to produce the Reynolds number. The distinc-

tion between laminar and turbulent pipe flow and its dependence on an appropriate dimensionless

quantity was first pointed out by Osborne Reynolds in 1883.

The Reynolds number ranges for which laminar, transitional, or turbulent pipe flows are ob-

tained cannot be precisely given. The actual transition from laminar to turbulent flow may take place

at various Reynolds numbers, depending on how much the flow is disturbed by vibrations of the pipe,

roughness of the entrance region, and the like. For general engineering purposes 1i.e., without undue

precautions to eliminate such disturbances2, the following values are appropriate: The flow in a round

pipe is laminar if the Reynolds number is less than approximately 2100. The flow in a round pipe is

turbulent if the Reynolds number is greater than approximately 4000. For Reynolds numbers between

these two limits, the flow may switch between laminar and turbulent conditions in an apparently ran-

dom fashion 1transitional flow2.

Re ⫽ rVD

Ⲑ

V ⫽ ui

⫹ vj

⫹ wk

V ⫽ ui

386 Chapter 8 ■ Viscous Flow in Pipes

F I G U R E 8.4 Time dependence of fluid velocity at a point.

Laminar

Transitional

Turbulent

Fluids in the News

Nanoscale flows The term nanoscale generally refers to objects

with characteristic lengths from atomic dimensions up to a few hun-

dred nanometers (nm). (Recall that .) Nanoscale

fluid mechanics research has recently uncovered many surprising

and useful phenomena. No doubt many more remain to be discov-

ered. For example, in the future researchers envision using

nanoscale tubes to push tiny amounts of water-soluble drugs to ex-

actly where they are needed in the human body. Because of the tiny

diameters involved, the Reynolds numbers for such flows are ex-

tremely small and the flow is definitely laminar. In addition, some

1 nm ⫽ 10

⫺9

standard properties of everyday flows (for example, the fact that a

fluid sticks to a solid boundary) may not be valid for nanoscale

flows. Also, ultratiny mechanical pumps and valves are difficult to

manufacture and may become clogged by tiny particles such as bio-

logical molecules. As a possible solution to such problems, re-

searchers have investigated the possibility of using a system that

does not rely on mechanical parts. It involves using light-sensitive

molecules attached to the surface of the tubes. By shining light onto

the molecules, the light-responsive molecules attract water and

cause motion of water through the tube. (See Problem 8.10.)

Pipe flow character-

istics are dependent

on the value of the

Reynolds number.

V8.3 Intermittent

turbulent burst in

pipe flow

JWCL068_ch08_383-460.qxd 9/23/08 10:50 AM Page 386