Munson B.R. Fundamentals of Fluid Mechanics

Подождите немного. Документ загружается.

Clearly the same fluid with and cannot be used in model and prototype unless

the length scale is unity 1which means that we are running tests on the prototype2. In high-speed

aerodynamics the prototype fluid is usually air, and it is difficult to satisfy Eq. 7.23 for reason-

able length scales. Thus, models involving high-speed flows are often distorted with respect to

Reynolds number similarity, but Mach number similarity is maintained.

7.9.3 Flow with a Free Surface

Flows in canals, rivers, spillways, and stilling basins, as well as flow around ships, are all exam-

ples of flow phenomena involving a free surface. For this class of problems, both gravitational and

inertial forces are important and, therefore, the Froude number becomes an important similarity

parameter. Also, since there is a free surface with a liquid–air interface, forces due to surface ten-

sion may be significant, and the Weber number becomes another similarity parameter that needs

to be considered along with the Reynolds number. Geometric variables will obviously still be im-

portant. Thus a general formulation for problems involving flow with a free surface can be ex-

pressed as

(7.24)

As discussed previously, is some characteristic length of the system, represents other pertinent

lengths, and is the relative roughness of the various surfaces. Since gravity is the driving force

in these problems, Froude number similarity is definitely required so that

The model and prototype are expected to operate in the same gravitational field and

therefore it follows that

(7.25)

Thus, when models are designed on the basis of Froude number similarity, the velocity scale is de-

termined by the square root of the length scale. As is discussed in Section 7.8.3, to simultaneously

have Reynolds and Froude number similarity it is necessary that the kinematic viscosity scale be

related to the length scale as

(7.26)

The working fluid for the prototype is normally either freshwater or seawater and the length scale

is small. Under these circumstances it is virtually impossible to satisfy Eq. 7.26, so models involv-

ing free-surface flows are usually distorted. The problem is further complicated if an attempt is made

to model surface tension effects, since this requires the equality of Weber numbers, which leads to

the condition

(7.27)

for the kinematic surface tension It is again evident that the same fluid cannot be used in

model and prototype if we are to have similitude with respect to surface tension effects for

Fortunately, in many problems involving free-surface flows, both surface tension and viscous

effects are small and consequently strict adherence to Weber and Reynolds number similarity is

not required. Certainly, surface tension is not important in large hydraulic structures and rivers.

Our only concern would be if in a model the depths were reduced to the point where surface ten-

sion becomes an important factor, whereas it is not in the prototype. This is of particular impor-

tance in the design of river models, since the length scales are typically small 1so that the width of

the model is reasonable2, but with a small length scale the required model depth may be very small.

To overcome this problem, different horizontal and vertical length scales are often used for river

 1.



r2.



 1l





 1l

 g2,



2g/



Dependent pi term  f a

rV/

2g/

n  n

c  c

7.9 Some Typical Model Studies 367

Froude number

similarity is usually

required for models

involving free-

surface flows.

V7.17 River flow

model

V7.18 Boat model

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 367

models. Although this approach eliminates surface tension effects in the model, it introduces geo-

metric distortion that must be accounted for empirically, usually by increasing the model surface

roughness. It is important in these circumstances that verification tests with the model be performed

1if possible2in which model data are compared with available prototype river flow data. Model

roughness can be adjusted to give satisfactory agreement between model and prototype, and then

the model subsequently used to predict the effect of proposed changes on river characteristics 1such

as velocity patterns or surface elevations2.

For large hydraulic structures, such as dam spillways, the Reynolds numbers are large so that

viscous forces are small in comparison to the forces due to gravity and inertia. In this case, Reynolds

number similarity is not maintained and models are designed on the basis of Froude number sim-

ilarity. Care must be taken to ensure that the model Reynolds numbers are also large, but they are

not required to be equal to those of the prototype. This type of hydraulic model is usually made

as large as possible so that the Reynolds number will be large. A spillway model is shown in Fig.

7.8. Also, for relatively large models the geometric features of the prototype can be accurately

scaled, as well as surface roughness. Note that which indicates that the model surfaces

must be smoother than the corresponding prototype surfaces for l

6 1.

⫽ l

368 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

F I G U R E 7.8 A scale hydraulic model

(1:197) of the Guri Dam in Venezuela which is used

to simulate the characteristics of the flow over and

below the spillway and the erosion below the spill-

way. (Photograph courtesy of St. Anthony Falls

Hydraulic Laboratory.)

V7.19 Dam model

Fluids in the News

Ice engineering Various types of models have been studied in

wind tunnels, water tunnels, and towing tanks for many years. But

another type of facility is needed to study ice and ice-related prob-

lems. The U.S. Army Cold Regions Research and Engineering

Laboratory has developed a unique complex that houses research

facilities for studies related to the mechanical behavior of ice and

ice–structure interactions. The laboratory contains three separate

cold-rooms—a test basin, a flume, and a general research area. In

the test basin, large-scale model studies of ice forces on structures

such as dams, piers, ships, and offshore platforms can be per-

formed. Ambient temperatures can be controlled as low as

and at this temperature a 2-mm per hour ice growth rate can be

achieved. It is also possible to control the mechanical properties of

the ice to properly match the physical scale of the model. Tests run

in the recirculating flume can simulate river processes during ice

formation. And in the large research area, scale models of lakes

and rivers can be built and operated to model ice interactions with

various types of engineering projects. (See Problem 7.73.)

⫺20 °F,

GIVEN The spillway for the dam shown in Fig. E7.8a is 20 m

wide and is designed to carry 125 m

/s at flood stage. A 1:15 model

is constructed to study the flow characteristics through the spillway.

The effects of surface tension and viscosity are to be neglected.

FIND

(a) Determine the required model width and flowrate.

(b) What operating time for the model corresponds to a 24-hr pe-

riod in the prototype?

F I G U R E E7.8

Froude Number Similarity

XAMPLE 7.8

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 368

There are, unfortunately, problems involving flow with a free surface in which viscous, in-

ertial, and gravitational forces are all important. The drag on a ship as it moves through water is

due to the viscous shearing stresses that develop along its hull, as well as a pressure-induced com-

ponent of drag caused by both the shape of the hull and wave action. The shear drag is a function

of the Reynolds number, whereas the pressure drag is a function of the Froude number. Since both

Reynolds number and Froude number similarity cannot be simultaneously achieved by using wa-

ter as the model fluid 1which is the only practical fluid for ship models2, some technique other than

a straightforward model test must be employed. One common approach is to measure the total drag

on a small, geometrically similar model as it is towed through a model basin at Froude numbers

matching those of the prototype. The shear drag on the model is calculated using analytical tech-

niques of the type described in Chapter 9. This calculated value is then subtracted from the total

drag to obtain pressure drag, and using Froude number scaling the pressure drag on the prototype

can then be predicted. The experimentally determined value can then be combined with a calcu-

lated value of the shear drag 1again using analytical techniques2to provide the desired total drag

7.9 Some Typical Model Studies 369

OLUTION

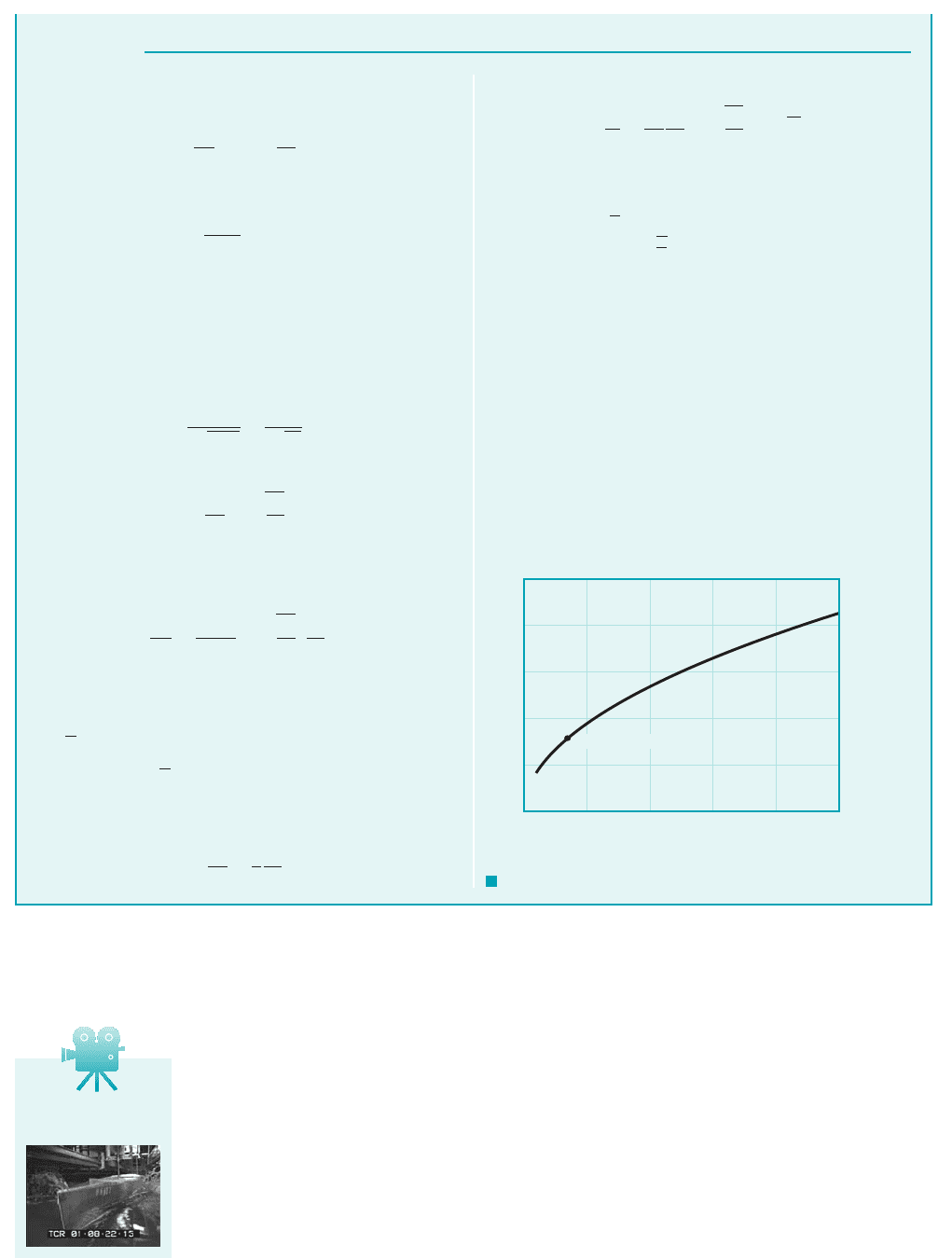
This result indicates that time intervals in the model will be

smaller than the corresponding intervals in the prototype if

For and a prototype time interval of 24 hr

(Ans)

COMMENT As indicated by the above analysis, the time

scale varies directly as the square root of the length scale. Thus,

as shown in Fig. E7.8b, the model time interval, , correspond-

ing to a 24-hr prototype time interval can be varied by changing

the length scale, . The ability to scale times may be very use-

ful, since it is possible to “speed up” events in the model which

may occur over a relatively long time in the prototype. There is

of course a practical limit to how small the length scale (and the

corresponding time scale) can become. For example, if the

length scale is too small then surface tension effects may

become important in the model whereas they are not in the pro-

totype. In such a case the present model design, based simply

on Froude number similarity, would not be adequate.

⫽ 2

124 hr2⫽ 6.20 hr

⫽

6 1.

⫽

⫽ 2l

The width, of the model spillway is obtained from the length

scale, so that

Therefore,

(Ans)

Of course, all other geometric features 1including surface rough-

ness2of the spillway must be scaled in accordance with the same

length scale.

With the neglect of surface tension and viscosity, Eq. 7.24 in-

dicates that dynamic similarity will be achieved if the Froude

numbers are equal between model and prototype. Thus,

and for

Since the flowrate is given by where A is an appropriate

cross-sectional area, it follows that

where we have made use of the relationship For

and

(Ans)

The time scale can be obtained from the velocity scale, since

the velocity is distance divided by time and therefore

⫽

1V ⫽ /

Ⲑ

t2,

⫽ 1

Ⲑ

1125 m

Ⲑ

s2⫽ 0.143 m

Ⲑ

Q ⫽ 125 m

Ⲑ

⫽

Ⲑ

A ⫽ 1/

Ⲑ

⫽ 1l

Ⲑ

⫽

Q ⫽ VA,

⫽

⫽ g

⫽

2g/

⫽

20 m

⫽ 1.33 m

⫽ l

⫽

0 0.1 0.2

ᐉ

___

ᐉ

0.3 0.4 0.5

, hr

(1/15, 6.20 hr)

F I G U R E E7.8

V7.20 Testing of

large yacht mode

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 369

on the ship. Ship models are widely used to study new designs, but the tests require extensive fa-

cilities 1see Fig. 7.92.

It is clear from this brief discussion of various types of models involving free-surface flows

that the design and use of such models requires considerable ingenuity, as well as a good under-

standing of the physical phenomena involved. This is generally true for most model studies. Mode-

ling is both an art and a science. Motion picture producers make extensive use of model ships,

fires, explosions, and the like. It is interesting to attempt to observe the flow differences between

these distorted model flows and the real thing.

370 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

F I G U R E 7.9 Instru-

mented, small-waterplane-area, twin

hull (SWATH) model suspended from

a towing carriage. (Photograph cour-

tesy of the U.S. Navy’s David W.

Taylor Research Center.)

In the preceding sections of this chapter, dimensional analysis has been used to obtain similarity

laws. This is a simple, straightforward approach to modeling, which is widely used. The use of di-

mensional analysis requires only a knowledge of the variables that influence the phenomenon of

interest. Although the simplicity of this approach is attractive, it must be recognized that omission

of one or more important variables may lead to serious errors in the model design. An alternative

approach is available if the equations 1usually differential equations2governing the phenomenon

are known. In this situation similarity laws can be developed from the governing equations, even

though it may not be possible to obtain analytic solutions to the equations.

To illustrate the procedure, consider the flow of an incompressible Newtonian fluid. For sim-

plicity we will restrict our attention to two-dimensional flow, although the results are applicable

to the general three-dimensional case. From Chapter 6 we know that the governing equations are

the continuity equation

(7.28)

and the Navier–Stokes equations

(7.29)

(7.30)

where the y axis is vertical, so that the gravitational body force, only appears in the “y equa-

tion.” To continue the mathematical description of the problem, boundary conditions are required.

For example, velocities on all boundaries may be specified; that is, and at all bound-

ary points and In some types of problems it may be necessary to specify the pres-

sure over some part of the boundary. For time-dependent problems, initial conditions would also

have to be provided, which means that the values of all dependent variables would be given at

some time 1usually taken at 2.

Once the governing equations, including boundary and initial conditions, are known, we are

ready to proceed to develop similarity requirements. The next step is to define a new set of

t ⫽ 0

y ⫽ y

.x ⫽ x

v ⫽ v

u ⫽ u

rg,

r a

⫹ u

⫹ v

b⫽⫺

⫺ rg ⫹ m a

⫹

r a

⫹ u

⫹ v

b⫽⫺

⫹ m a

⫹

⫽ 0

7.10 Similitude Based on Governing Differential Equations

Similarity laws can

be directly devel-

oped from the equa-

tions governing the

phenomenon of

interest.

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 370

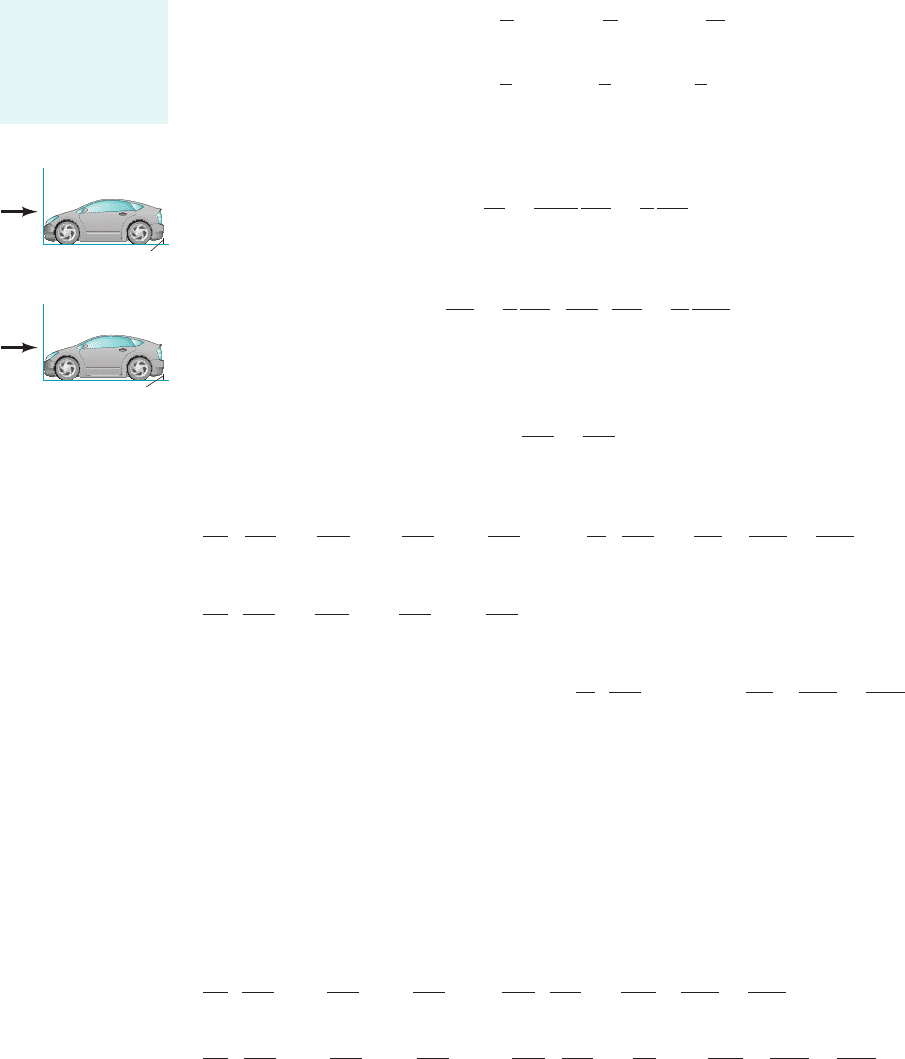
variables that are dimensionless. To do this we select a reference quantity for each type of vari-

able. In this problem the variables are and t so we will need a reference velocity, V,a

reference pressure, a reference length, and a reference time, These reference quantities

should be parameters that appear in the problem. For example, may be a characteristic length of

a body immersed in a fluid or the width of a channel through which a fluid is flowing. The veloc-

ity, V, may be the free-stream velocity or the inlet velocity. The new dimensionless 1starred2vari-

ables can be expressed as

as shown in the figure in the margin.

The governing equations can now be rewritten in terms of these new variables. For example,

and

The other terms that appear in the equations can be expressed in a similar fashion. Thus, in terms

of the new variables the governing equations become

(7.31)

and

(7.32)

(7.33)

The terms appearing in brackets contain the reference quantities and can be interpreted as indices

of the various forces 1per unit volume2that are involved. Thus, as is indicated in Eq. 7.33,

inertia 1local2force, inertia 1convective2force, pressure force, gravitational force,

and viscous force. As the final step in the nondimensionalization process, we will divide each

term in Eqs. 7.32 and 7.33 by one of the bracketed quantities. Although any one of these quanti-

ties could be used, it is conventional to divide by the bracketed quantity which is the index

of the convective inertia force. The final nondimensional form then becomes

(7.34)

(7.35)

We see that bracketed terms are the standard dimensionless groups 1or their reciprocals2which

were developed from dimensional analysis; that is, is a form of the Strouhal number, p

Ⲑ

⫽⫺c

0p*

0y*

⫺ c

d⫹ c

rV/

d a

0x*

⫹

0y*

0v*

0t*

⫹ u*

0v*

0x*

⫹ v*

0v*

0y*

0u*

0t*

⫹ u*

0u*

0x*

⫹ v*

0u*

0y*

⫽⫺c

0p*

0x*

⫹ c

rV/

0x*

⫹

0y*

Ⲑ

⫽

⫽F

⫽

冧

⫽⫺c

0p*

0y*

⫺ 3rg4⫹ c

d a

0x*

⫹

0y*

冧

0v*

0t*

⫹ c

au*

0v*

0x*

⫹ v*

0v*

0y*

0u*

0t*

⫹ c

d au*

0u*

0x*

⫹ v*

0u*

0y*

b⫽⫺c

0p*

0x*

⫹ c

d a

0x*

⫹

0y*

0u*

0x*

⫹

0v*

0y*

⫽ 0

⫽

0x*

0u*

0x*

⫽

0x*

⫽

0Vu*

0x*

⫽

0u*

0x*

x* ⫽

y* ⫽

t* ⫽

u* ⫽

v* ⫽

p* ⫽

t./,p

u, v, p, x, y,

7.10 Similitude Based on Governing Differential Equations 371

Each variable is

made dimensionless

by dividing by an

appropriate refer-

ence quantity.

u = V

= ᐉ

= 0

= p

Actual

u* = 1

x* = 1

v* = 0

* = 1

Dimensionless

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 371

the Euler number, the reciprocal of the square of the Froude number, and the recip-

rocal of the Reynolds number. From this analysis it is now clear how each of the dimensionless

groups can be interpreted as the ratio of two forces, and how these groups arise naturally from the

governing equations.

Although we really have not helped ourselves with regard to obtaining an analytical solution

to these equations 1they are still complicated and not amenable to an analytical solution2, the di-

mensionless forms of the equations, Eqs. 7.31, 7.34, and 7.35, can be used to establish similarity

requirements. From these equations it follows that if two systems are governed by these equations,

then the solutions will be the same if the four parameters

and are equal for the two systems. The two systems will be dynam-

ically similar. Of course, boundary and initial conditions expressed in dimensionless form must

also be equal for the two systems, and this will require complete geometric similarity. These are

the same similarity requirements that would be determined by a dimensional analysis if the same

variables were considered. However, the advantage of working with the governing equations is that

the variables appear naturally in the equations, and we do not have to worry about omitting an im-

portant one, provided the governing equations are correctly specified. We can thus use this method

to deduce the conditions under which two solutions will be similar even though one of the solu-

tions will most likely be obtained experimentally.

In the foregoing analysis we have considered a general case in which the flow may be

unsteady, and both the actual pressure level, and the effect of gravity are important. A

reduction in the number of similarity requirements can be achieved if one or more of these con-

ditions is removed. For example, if the flow is steady the dimensionless group, can be

eliminated.

The actual pressure level will only be of importance if we are concerned with cavitation. If not,

the flow patterns and the pressure differences will not depend on the pressure level. In this case,

can be taken as and the Euler number can be eliminated as a similarity requirement.

However, if we are concerned about cavitation 1which will occur in the flow field if the pressure at

certain points reaches the vapor pressure, 2, then the actual pressure level is important. Usually, in

this case, the characteristic pressure, is defined relative to the vapor pressure such that

where is some reference pressure within the flow field. With defined in this manner, the simi-

larity parameter becomes This parameter is frequently written as

and in this form, as was noted previously in Section 7.6, is called the cavitation num-

ber. Thus we can conclude that if cavitation is not of concern we do not need a similarity parameter

involving , but if cavitation is to be modeled, then the cavitation number becomes an important

similarity parameter.

The Froude number, which arises because of the inclusion of gravity, is important for prob-

lems in which there is a free surface. Examples of these types of problems include the study of

rivers, flow through hydraulic structures such as spillways, and the drag on ships. In these situa-

tions the shape of the free surface is influenced by gravity, and therefore the Froude number be-

comes an important similarity parameter. However, if there are no free surfaces, the only effect of

gravity is to superimpose a hydrostatic pressure distribution on the pressure distribution created by

the fluid motion. The hydrostatic distribution can be eliminated from the governing equation 1Eq.

7.302by defining a new pressure, and with this change the Froude number does not

appear in the nondimensional governing equations.

We conclude from this discussion that for the steady flow of an incompressible fluid with-

out free surfaces, dynamic and kinematic similarity will be achieved if 1for geometrically similar

systems2Reynolds number similarity exists. If free surfaces are involved, Froude number similar-

ity must also be maintained. For free-surface flows we have tacitly assumed that surface tension

is not important. We would find, however, that if surface tension is included, its effect would ap-

pear in the free-surface boundary condition, and the Weber number, would become an ad-

ditional similarity parameter. In addition, if the governing equations for compressible fluids are

considered, the Mach number, would appear as an additional similarity parameter.

It is clear that all the common dimensionless groups that we previously developed by using

dimensional analysis appear in the governing equations that describe fluid motion when these equa-

tions are expressed in terms of dimensionless variables. Thus, the use of the governing equations

to obtain similarity laws provides an alternative to dimensional analysis. This approach has the

Ⲑ

p¿ ⫽ p ⫺ rgy,

1 p

⫺ p

Ⲑ

1 p

⫺ p

Ⲑ

⫽ p

⫺ p

1or

Ⲑ

tV,

rV/

Ⲑ

tV, p

Ⲑ

, V

Ⲑ

g/,

1in terms of u*, v*, p*, x*, y*, and t*2

Ⲑ

rV/g/

Ⲑ

372 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

Governing equa-

tions expressed in

terms of dimension-

less variables lead

to the appropriate

dimensionless

groups.

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 372

advantage that the variables are known and the assumptions involved are clearly identified. In ad-

dition, a physical interpretation of the various dimensionless groups can often be obtained.

7.11 Chapter Summary and Study Guide 373

7.11 Chapter Summary and Study Guide

similitude

dimensionless product

basic dimensions

pi term

Buckingham pi theorem

method of repeating

variables

model

modeling laws

prototype

prediction equation

model design conditions

similarity requirements

modeling laws

length scale

distorted model

true model

Many practical engineering problems involving fluid mechanics require experimental data for their

solution. Thus, laboratory studies and experimentation play a significant role in this field. It is impor-

tant to develop good procedures for the design of experiments so they can be efficiently completed

with as broad applicability as possible. To achieve this end the concept of similitude is often used in

which measurements made in the laboratory can be utilized for predicting the behavior of other sim-

ilar systems. In this chapter, dimensional analysis is used for designing such experiments, as an aid

for correlating experimental data, and as the basis for the design of physical models. As the name

implies, dimensional analysis is based on a consideration of the dimensions required to describe the

variables in a given problem. A discussion of the use of dimensions and the concept of dimensional

homogeneity (which forms the basis for dimensional analysis) was included in Chapter 1.

Essentially, dimensional analysis simplifies a given problem described by a certain set of vari-

ables by reducing the number of variables that need to be considered. In addition to being fewer in

number, the new variables are dimensionless products of the original variables. Typically these new

dimensionless variables are much simpler to work with in performing the desired experiments. The

Buckingham pi theorem, which forms the theoretical basis for dimensional analysis, is introduced. This

theorem establishes the framework for reducing a given problem described in terms of a set of vari-

ables to a new set of fewer dimensionless variables. A simple method, called the repeating variable

method, is described for actually forming the dimensionless variables (often called pi terms). Forming

dimensionless variables by inspection is also considered. It is shown how the use of dimensionless vari-

ables can be of assistance in planning experiments and as an aid in correlating experimental data.

For problems in which there are a large number of variables, the use of physical models is

described. Models are used to make specific predictions from laboratory tests rather than formu-

lating a general relationship for the phenomenon of interest. The correct design of a model is

obviously imperative for the accurate predictions of other similar, but usually larger, systems. It

is shown how dimensional analysis can be used to establish a valid model design. An alternative

approach for establishing similarity requirements using governing equations (usually differential

equations) is presented.

The following checklist provides a study guide for this chapter. When your study of the

entire chapter and end-of-chapter exercies has been completed you should be able to

write out meanings of the terms listed here in the margin and understand each of the related

concepts. These terms are particularly important and are set in italic, bold, and color type

in the text.

use the Buckingham pi theorem to determine the number of independent dimensionless vari-

ables needed for a given flow problem.

form a set of dimensionless variables using the method of repeating variables.

form a set of dimensionless variables by inspection.

use dimensionless variables as an aid in interpreting and correlating experimental data.

use dimensional analysis to establish a set of similarity requirements (and prediction equa-

tion) for a model to be used to predict the behavior of another similar system (the prototype).

rewrite a given governing equation in a suitable nondimensional form and deduce similar-

ity requirements from the nondimensional form of the equation.

Some of the important equations in this chapter are:

Reynolds number

Froude number Fr ⫽

1g/

Re ⫽

rV/

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 373

374 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

Go to Appendix G for a set of review problems with answers. De-

tailed solutions can be found in Student Solution Manual and Study

Guide for Fundamentals of Fluid Mechanics, by Munson et al.

Review Problems

Note: Unless otherwise indicated, use the values of fluid prop-

erties found in the tables on the inside of the front cover. Prob-

lems designated with an 1

*2are intended to be solved with the aid

of a programmable calculator or a computer. Problems desig-

nated with a 1

†2are “open-ended” problems and require critical

thinking in that to work them one must make various assump-

tions and provide the necessary data. There is not a unique an-

swer to these problems.

Answers to the even-numbered problems are listed at the

end of the book. Access to the videos that accompany problems

can be obtained through the book’s web site, www.wiley.com/

college/munson. The lab-type problems and FlowLab problems

can also be accessed on this web site.

Section 7.1 Dimensional Analysis

7.1 Obtain a photograph/image of an experimental setup used to in-

vestigate some type of fluid flow phenomena. Print this photo and

write a brief paragraph that describes the situation involved.

7.2 Verify the left-hand side of Eq. 7.2 is dimensionless using the

MLT system.

7.3 The Reynolds number, is a very important parameter in

fluid mechanics. Verify that the Reynolds number is dimensionless,

using both the FLT system and the MLT system for basic dimen-

sions, and determine its value for ethyl alcohol flowing at a velocity

of 3 m兾s through a 2-in.-diameter pipe.

rVD

Ⲑ

Problems

Euler number

Cauchy number

Mach number

Strouhal number

Weber number

References

1. Bridgman, P. W., Dimensional Analysis, Yale University Press, New Haven, Conn., 1922.

2. Murphy, G., Similitude in Engineering, Ronald Press, New York, 1950.

3. Langhaar, H. L., Dimensional Analysis and Theory of Models, Wiley, New York, 1951.

4. Huntley, H. E., Dimensional Analysis, Macdonald, London, 1952.

5. Duncan, W. J., Physical Similarity and Dimensional Analysis: An Elementary Treatise, Edward Arnold,

London, 1953.

6. Sedov, K. I., Similarity and Dimensional Methods in Mechanics, Academic Press, New York, 1959.

7. Ipsen, D. C., Units, Dimensions, and Dimensionless Numbers, McGraw-Hill, New York, 1960.

8. Kline, S. J., Similitude and Approximation Theory, McGraw-Hill, New York, 1965.

9. Skoglund, V. J., Similitude—Theory and Applications, International Textbook, Scranton, Pa., 1967.

10. Baker, W. E., Westline, P. S., and Dodge, F. T., Similarity Methods in Engineering Dynamics—Theory

and Practice of Scale Modeling, Hayden 1Spartan Books2, Rochelle Park, N.J., 1973.

11. Taylor, E. S., Dimensional Analysis for Engineers, Clarendon Press, Oxford, 1974.

12. Isaacson, E. de St. Q., and Isaacson, M. de St. Q., Dimensional Methods in Engineering and Physics,

Wiley, New York, 1975.

13. Schuring, D. J., Scale Models in Engineering, Pergamon Press, New York, 1977.

14. Yalin, M. S., Theory of Hydraulic Models, Macmillan, London, 1971.

15. Sharp, J. J., Hydraulic Modeling, Butterworth, London, 1981.

16. Schlichting, H., Boundary-Layer Theory, 7th Ed., McGraw-Hill, New York, 1979.

17. Knapp, R. T., Daily, J. W., and Hammitt, F. G., Cavitation, McGraw-Hill, New York, 1970.

We ⫽

St ⫽

Ma ⫽

Ca ⫽

Eu ⫽

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 374

7.4 What are the dimensions of acceleration of gravity, density,

dynamic viscosity, kinematic viscosity, specific weight, and speed

of sound in (a) the FLT system, and (b) the MLT system? Compare

your results with those given in Table 1.1 in Chapter 1.

7.5 For the flow of a thin film of a liquid with a depth h and a free

surface, two important dimensionless parameters are the Froude

number, and the Weber number, Determine the

value of these two parameters for glycerin flowing with

a velocity of 0.7 m兾s at a depth of 3 mm.

7.6 The Mach number for a body moving through a fluid with ve-

locity V is defined as where c is the speed of sound in the fluid.

This dimensionless parameter is usually considered to be important

in fluid dynamics problems when its value exceeds 0.3. What

would be the velocity of a body at a Mach number of 0.3 if the fluid

is (a) air at standard atmospheric pressure and and (b) water

at the same temperature and pressure?

Section 7.3 Determination of Pi Terms

7.7 Obtain a photograph/image of Osborne Reynolds, who devel-

oped the famous dimensionless quantity, the Reynolds number.

Print this photo and write a brief paragraph about him.

7.8 The power,

, required to run a pump that moves fluid within

a piping system is dependent upon the volume flowrate, Q, den-

sity, ␳, impeller diameter, d, angular velocity, , and fluid viscos-

ity, ␮. Find the number of pi terms for this relationship.

7.9 For low speed flow over a flat plate, one measure of the bound-

ary layer is the resulting thickness, , at a given downstream location.

The boundary layer thickness is a function of the free stream veloc-

ity, , fluid density and viscosity ␳ and ␮, and the distance from the

leading edge, x. Find the number of pi terms for this relationship.

7.10 The excess pressure inside a bubble (discussed in Chapter 1)

is known to be dependent on bubble radius and surface tension. Af-

ter finding the pi terms, determine the variation in excess pressure

if we (a) double the radius and (b) double the surface tension.

7.11 It is known that the variation of pressure, within a static

fluid is dependent upon the specific weight of the fluid and the ele-

vation difference, . Using dimensional analysis, find the form of

the hydrostatic equation for pressure variation.

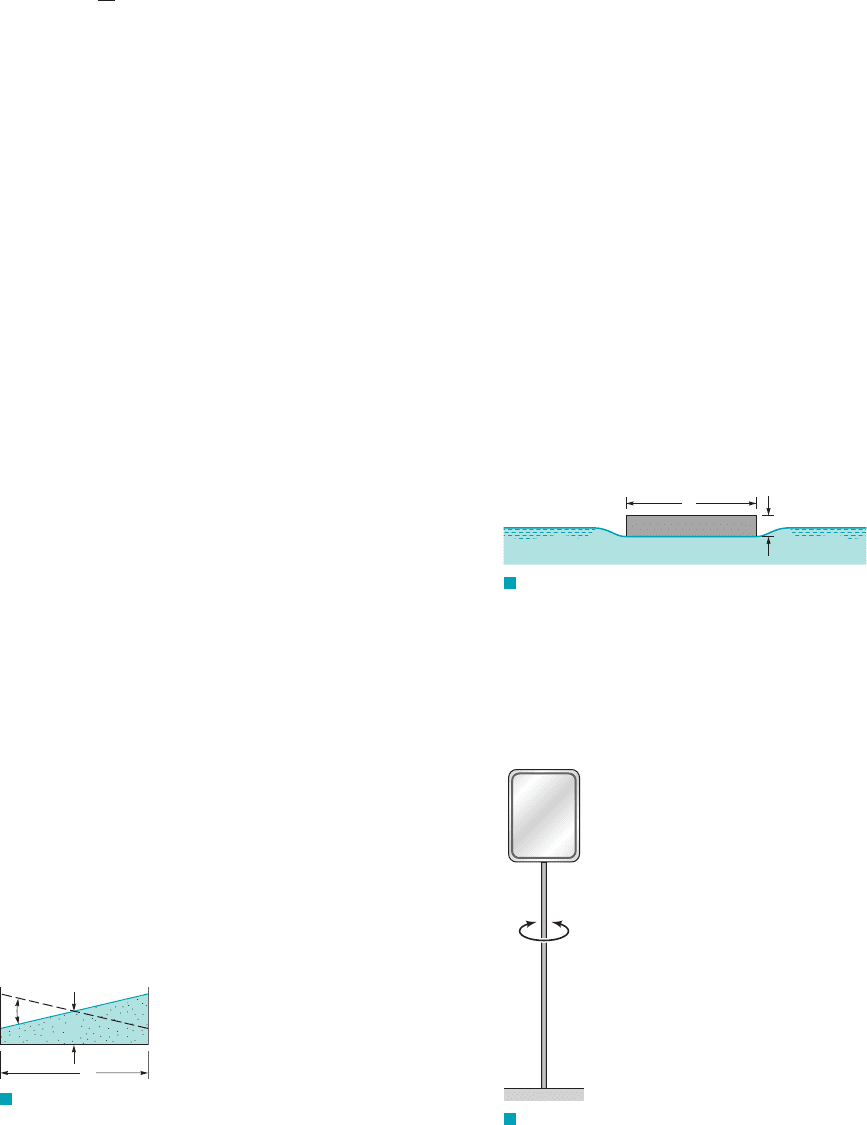
7.12 At a sudden contraction in a pipe the diameter changes from

The pressure drop, which develops across the con-

traction is a function of as well as the velocity, V, in the

larger pipe, and the fluid density, and viscosity, Use

as repeating variables to determine a suitable set of

dimensionless parameters. Why would it be incorrect to include

the velocity in the smaller pipe as an additional variable?

7.13 Water sloshes back and forth in a tank as shown in Fig. P7.13.

The frequency of sloshing, is assumed to be a function of the ac-

celeration of gravity, g, the average depth of the water, h, and the

length of the tank, Develop a suitable set of dimensionless para-

meters for this problem using g and as repeating variables./

, V, and m

m.r,

and D

¢p,D

to D

¢z

¢p,

20 °C,

Ⲑ

1at 20 °C2

Ⲑ

s.V

Ⲑ

1gh,

7.15 Assume that the flowrate, Q, of a gas from a smokestack is a

function of the density of the ambient air, , the density of the gas,

, within the stack, the acceleration of gravity, g, and the height and

diameter of the stack, h and d, respectively. Use , d, and g as re-

peating variables to develop a set of pi terms that could be used to

describe this problem.

7.16 The pressure rise, across a pump can be expressed as

where D is the impeller diameter, the fluid density, the

rotational speed, and Q the flowrate. Determine a suitable set of

dimensionless parameters.

7.17 A thin elastic wire is placed between rigid supports. A fluid

flows past the wire, and it is desired to study the static deflection, , at

the center of the wire due to the fluid drag. Assume that

where is the wire length, d the wire diameter, the fluid den-

sity, the fluid viscosity, V the fluid velocity, and E the modulus

of elasticity of the wire material. Develop a suitable set of pi terms

for this problem.

7.18 Because of surface tension, it is possible, with care, to support

an object heavier than water on the water surface as shown in Fig.

P7.18. (See Video V1.9.) The maximum thickness, h, of a square of

material that can be supported is assumed to be a function of the

length of the side of the square, the density of the material, the

acceleration of gravity, g, and the surface tension of the liquid,

Develop a suitable set of dimensionless parameters for this problem.

r,/,

d ⫽ f1/, d, r, m, V, E2

¢p ⫽ f1D, r, v, Q2

¢p,

Problems 375

ᐉ

F I G U R E P7.13

7.14 Assume that the power, , required to drive a fan is a function

of the fan diameter, D, the fluid density, ␳, the rotational speed, ,

and the flowrate, Q. Use D, , and ␳ as repeating variables to de-

termine a suitable set of pi terms.

ᐉ

F I G U R E P7.18

7.19 Under certain conditions, wind blowing past a rectangular speed

limit sign can cause the sign to oscillate with a frequency (See Fig.

P7.19 and Video V9.9.) Assume that is a function of the sign width,

b, sign height, h, wind velocity, V, air density, and an elastic con-

stant, k, for the supporting pole. The constant,k, has dimensions of FL.

Develop a suitable set of pi terms for this problem.

SPEED

LIMIT

F I G U R E P7.19

7.20 The height, h, that a liquid will rise in a capillary tube is a

function of the tube diameter, D, the specific weight of the liquid,

and the surface tension, Perform a dimensional analysis usings.g,

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 375

both the FLT and MLT systems for basic dimensions. Note: the re-

sults should obviously be the same regardless of the system of di-

mensions used. If your analysis indicates otherwise, go back and

check your work, giving particular attention to the required number

of reference dimensions.

7.21 A cone and plate viscometer consists of a cone with a very

small angle which rotates above a flat surface as shown in

Fig. P7.21. The torque, , required to rotate the cone at an angular

velocity is a function of the radius, R, the cone angle, , and the

fluid viscosity, , in addition to . With the aid of dimensional

analysis, determine how the torque will change if both the viscosity

and angular velocity are doubled.

᐀

376 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

F I G U R E P7.21

᐀

Fluid

7.22 The pressure drop, , along a straight pipe of diameter D has

been experimentally studied, and it is observed that for laminar flow

of a given fluid and pipe, the pressure drop varies directly with the

distance, between pressure taps. Assume that is a function of

D and the velocity, V, and the fluid viscosity, Use dimensional

analysis to deduce how the pressure drop varies with pipe diameter.

7.23 A cylinder with a diameter D floats upright in a liquid as

shown in Fig. P7.23. When the cylinder is displaced slightly along

its vertical axis it will oscillate about its equilibrium position with a

frequency, Assume that this frequency is a function of the diam-

eter, D, the mass of the cylinder, m, and the specific weight, of

the liquid. Determine, with the aid of dimensional analysis, how the

frequency is related to these variables. If the mass of the cylinder

were increased, would the frequency increase or decrease?

m./,

¢p/,

¢p

F I G U R E P7.23

Cylinder

diameter =

Section 7.5 Determination of Pi Terms by Inspection

7.24 A liquid spray nozzle is designed to produce a specific size

droplet with diameter, d. The droplet size depends on the nozzle di-

ameter, D, nozzle velocity, V, and the liquid properties . Us-

ing the common dimensionless terms found in Table 7.1, determine

the functional relationship for the dependent diameter ratio of

7.25 The velocity, c, at which pressure pulses travel through arter-

ies (pulse-wave velocity) is a function of the artery diameter, D, and

wall thickness, h, the density of blood, , and the modulus of elas-

ticity, E, of the arterial wall. Determine a set of nondimensional pa-

rameters that can be used to study experimentally the relationship



r, m, s

between the pulse-wave velocity and the variables listed. Form the

nondimensional parameters by inspection.

7.26 As shown in Fig. P7.26 and Video V5.6, a jet of liquid di-

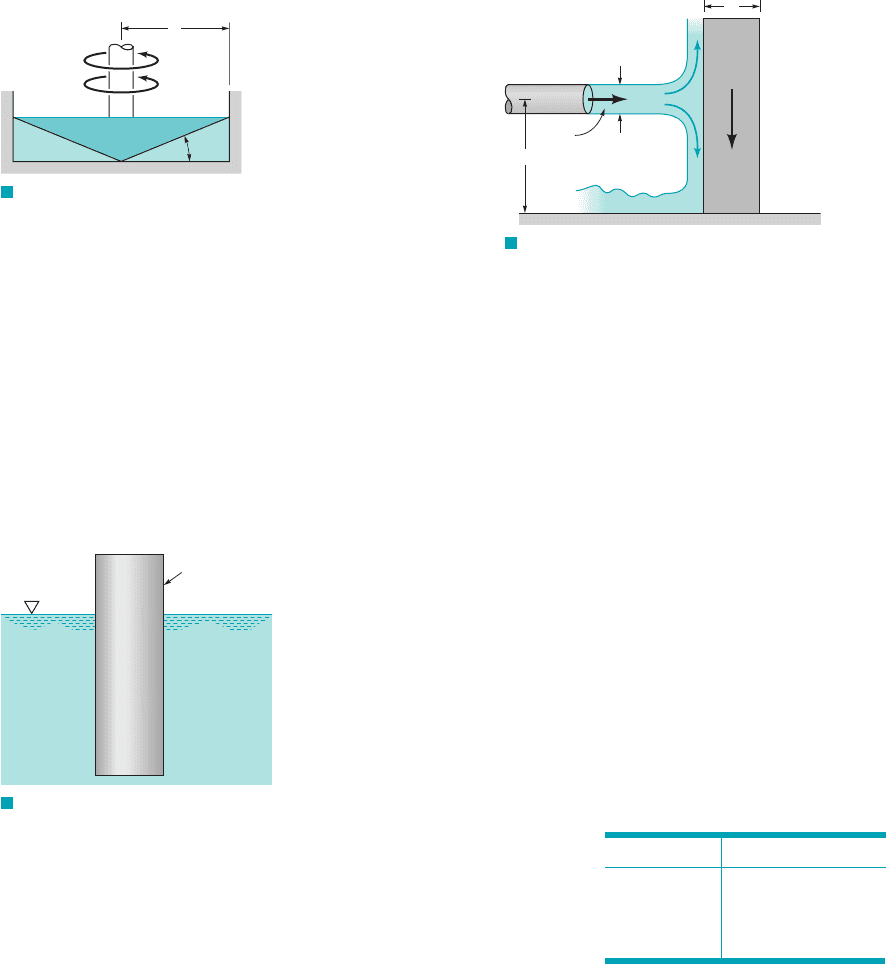
rected against a block can tip over the block. Assume that the veloc-

ity, V, needed to tip over the block is a function of the fluid density,

the diameter of the jet, D, the weight of the block, the width

of the block, b, and the distance, d, between the jet and the bottom

of the block. (a) Determine a set of dimensionless parameters for

this problem. Form the dimensionless parameters by inspection. (b)

Use the momentum equation to determine an equation for V in terms

of the other variables. (c) Compare the results of parts (a) and (b).

w,r,

ᐃ

F I G U R E P7.26

7.27 Assume that the drag, on an aircraft flying at supersonic

speeds is a function of its velocity, V, fluid density, speed of

sound, c, and a series of lengths, which describe the

geometry of the aircraft. Develop a set of pi terms that could

be used to investigate experimentally how the drag is affected by

the various factors listed. Form the pi terms by inspection.

Section 7.7 Correlation of Experimental Data (Also See

Lab Problems 7.82, 7.83, 7.84, and 7.85)

7.28 The measurement of pressure is typically an important task in

fluids experiments. Obtain a photograph/image of a pressure mea-

surement device. Print this photo and write a brief paragraph that

describes its use.

*7.29 The pressure drop, over a certain length of horizontal

pipe is assumed to be a function of the velocity, V, of the fluid in the

pipe, the pipe diameter, D, and the fluid density and viscosity, and

(a) Show that this flow can be described in dimensionless form as

a “pressure coefficient,” that depends on the

Reynolds number, (b) The following data were ob-

tained in an experiment involving a fluid with

and Plot a dimensionless graph

and use a power law equation to determine the functional relationship

between the pressure coefficient and the Reynolds number. (c) What

are the limitations on the applicability of your equation obtained in

part (b)?

D  0.1 ft.m  2  10

3



r  2 slugs/ft

Re  rVD



 ¢p



10.5 rV

¢p,

, . . . , /

3 192

11 704

17 1088

20 1280

¢p, lb



V, ft



*7.30 The pressure drop across a short hollowed plug placed in a

circular tube through which a liquid is flowing (see Fig. P7.30) can

be expressed as

¢p  f 1r, V, D, d2

JWCL068_ch07_332-382.qxd 9/23/08 10:47 AM Page 376