Munson B.R. Fundamentals of Fluid Mechanics

Подождите немного. Документ загружается.

7.8 Modeling and Similitude 357

GIVEN A long structural component of a bridge has an elliptical

cross section shown in Fig. E7.5. It is known that when a steady wind

blows past this type of bluff body, vortices may develop on the down-

wind side that are shed in a regular fashion at some definite fre-

quency. Since these vortices can create harmful periodic forces acting

on the structure, it is important to determine the shedding frequency.

For the specific structure of interest, and aH  0.3 m,D  0.1 m,

OLUTION

F I G U R E E7.5

Prediction of Prototype Performance from Model Data

The second similarity requirement indicates that the Reynolds

number must be the same for model and prototype so that the

model velocity must satisfy the condition

(1)

For air at standard conditions,

and for water at

The fluid velocity for the proto-

type is

The required velocity can now be calculated from Eq. 1 as

(Ans)

This is a reasonable velocity that could be readily achieved in a

water tunnel.

With the two similarity requirements satisfied, it follows that

the Strouhal numbers for prototype and model will be the same so

that

and the predicted prototype vortex shedding frequency is

(Ans)

v  29.0 Hz



113.9 m



14.79 m



120  10

3

10.1 m2

149.9 Hz2

v 



 4.79 m





10.1 m2

120  10

3

113.9 m





31.00  10

3



s24

31.79  10

5



s24

11.23 kg



1998 kg



V 

150  10



hr2

13600 s



hr2

 13.9 m



3



s, r  998 kg



m  1.00 20 °C,

r  1.23 kg



m  1.79  10

5





XAMPLE 7.5

We expect the shedding frequency, to depend on the lengths D

and H, the approach velocity, V, and the fluid density, and vis-

cosity, Thus,

where

Since there are six variables and three reference dimensions 1MLT2,

three pi terms are required. Application of the pi theorem yields

We recognize the pi term on the left as the Strouhal number, and

the dimensional analysis indicates that the Strouhal number is a

function of the geometric parameter, and the Reynolds num-

ber. Thus, to maintain similarity between model and prototype

and

From the first similarity requirement

(Ans)

 60  10

3

m  60 mm



120  10

3

10.1 m2

10.3 m2



rVD





 f a

rVD

m ⬟ ML

1

r ⬟ ML

3

V ⬟ LT

1

H ⬟ L

D ⬟ L

v ⬟ T

1

v  f1D, H, V, r, m2

V7.10 Flow past an

ellipse

representative wind velocity is 50 km兾hr. Standard air can be as-

sumed. The shedding frequency is to be determined through the use

of a small-scale model that is to be tested in a water tunnel. For the

model and the water temperature is

FIND Determine the model dimension, and the velocity at

which the test should be performed. If the shedding frequency for

the model is found to be 49.9 Hz, what is the corresponding fre-

quency for the prototype?

20 °C.

 20 mm

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 357

7.8.2 Model Scales

It is clear from the preceding section that the ratio of like quantities for the model and prototype

naturally arises from the similarity requirements. For example, if in a given problem there are two

length variables and the resulting similarity requirement based on a pi term obtained from

these two variables is

so that

We define the ratio or as the length scale. For true models there will be only one length

scale, and all lengths are fixed in accordance with this scale. There are, however, other scales such

as the velocity scale, density scale, viscosity scale, and so on. In fact, we can de-

fine a scale for each of the variables in the problem. Thus, it is actually meaningless to talk about

a “scale” of a model without specifying which scale.

We will designate the length scale as and other scales as and so on, where the

subscript indicates the particular scale. Also, we will take the ratio of the model value to the pro-

totype value as the scale 1rather than the inverse2. Length scales are often specified, for example,

as 1 : 10 or as a scale model. The meaning of this specification is that the model is one-tenth

the size of the prototype, and the tacit assumption is that all relevant lengths are scaled accord-

ingly so the model is geometrically similar to the prototype.

, l



m,r



r,V





358 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

COMMENT This same model could also be used to predict

the drag per unit length, 1lb兾ft or N兾m2, on the prototype, since

the drag would depend on the same variables as those used for the

frequency. Thus, the similarity requirements would be the same

and with these requirements satisfied it follows that the drag per

unit length expressed in dimensionless form, such as



DrV

would be equal in model and prototype. The measured drag per

unit length on the model could then be related to the correspond-

ing drag per unit length on the prototype through the relationship

 a

b a

The ratio of a

model variable to

the corresponding

prototype variable

is called the scale

for that variable.

Fluids in the News

“Galloping Gertie” One of the most dramatic bridge collapses

occurred in 1940 when the Tacoma Narrows bridge, located near

Tacoma, Washington, failed due to aerodynamic instability. The

bridge had been nicknamed “Galloping Gertie” due to its tendency

to sway and move in high winds. On the fateful day of the collapse

the wind speed was . This particular combination of a

high wind and the aeroelastic properties of the bridge created large

oscillations leading to its failure. The bridge was replaced in 1950,

and plans are underway to add a second bridge parallel to the ex-

65 km



isting structure. To determine possible wind interference effects

due to two bridges in close proximity, wind tunnel tests were run

in a wind tunnel operated by the National Research

Council of Canada. Models of the two side-by-side bridges, each

having a length scale of 1 : 211, were tested under various wind

conditions. Since the failure of the original Tacoma Narrows

bridge, it is now common practice to use wind tunnel model stud-

ies during the design process to evaluate any bridge that is to be

subjected to wind-induced vibrations. (See Problem 7.72.)

9 m  9 m

7.8.3 Practical Aspects of Using Models

Validation of Model Design. Most model studies involve simplifying assumptions with

regard to the variables to be considered. Although the number of assumptions is frequently less

stringent than that required for mathematical models, they nevertheless introduce some uncer-

tainty in the model design. It is, therefore, desirable to check the design experimentally when-

ever possible. In some situations the purpose of the model is to predict the effects of certain proposed

changes in a given prototype, and in this instance some actual prototype data may be available.

The model can be designed, constructed, and tested, and the model prediction can be compared

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 358

with these data. If the agreement is satisfactory, then the model can be changed in the desired

manner, and the corresponding effect on the prototype can be predicted with increased confi-

dence.

Another useful and informative procedure is to run tests with a series of models of different

sizes, where one of the models can be thought of as the prototype and the others as “models” of this

prototype. With the models designed and operated on the basis of the proposed design, a necessary

condition for the validity of the model design is that an accurate prediction be made between any

pair of models, since one can always be considered as a model of the other. Although suitable agree-

ment in validation tests of this type does not unequivocally indicate a correct model design 1e.g., the

length scales between laboratory models may be significantly different than required for actual pro-

totype prediction2, it is certainly true that if agreement between models cannot be achieved in these

tests, there is no reason to expect that the same model design can be used to predict prototype be-

havior correctly.

Distorted Models. Although the general idea behind establishing similarity requirements

for models is straightforward 1we simply equate pi terms2, it is not always possible to satisfy all

the known requirements. If one or more of the similarity requirements are not met, for example,

if then it follows that the prediction equation is not true; that is,

Models for which one or more of the similarity requirements are not satisfied are called distorted

models.

Distorted models are rather commonplace, and they can arise for a variety of reasons. For

example, perhaps a suitable fluid cannot be found for the model. The classic example of a dis-

torted model occurs in the study of open channel or free-surface flows. Typically, in these prob-

lems both the Reynolds number, and the Froude number, are involved.

Froude number similarity requires

If the model and prototype are operated in the same gravitational field, then the required velocity

scale is

Reynolds number similarity requires

and the velocity scale is

Since the velocity scale must be equal to the square root of the length scale, it follows that

(7.15)

where the ratio is the kinematic viscosity, Although in principle it may be possible to sat-

isfy this design condition, it may be quite difficult, if not impossible, to find a suitable model fluid,

particularly for small length scales. For problems involving rivers, spillways, and harbors, for which

the prototype fluid is water, the models are also relatively large so that the only practical model

fluid is water. However, in this case 1with the kinematic viscosity scale equal to unity2Eq. 7.15

will not be satisfied, and a distorted model will result. Generally, hydraulic models of this type are

distorted and are designed on the basis of the Froude number, with the Reynolds number different

in model and prototype.

Distorted models can be successfully used, but the interpretation of results obtained with this

type of model is obviously more difficult than the interpretation of results obtained with true mod-

els for which all similarity requirements are met. There are no general rules for handling distorted

n.m

Ⲑ

⫽

⫽ 1l

Ⲑ

⫽

rV/

⫽

⫽ 1l

⫽

1g/

Ⲑ

1g/,rV/

Ⲑ

Zß

.ß

⫽ ß

Zß

7.8 Modeling and Similitude 359

Models for which

one or more simi-

larity requirements

are not satisfied

are called distorted

models.

V7.12 Distorted

river model

V7.11 Model of

fish hatchery pond

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 359

models, and essentially each problem must be considered on its own merits. The success of using

distorted models depends to a large extent on the skill and experience of the investigator responsible

for the design of the model and in the interpretation of experimental data obtained from the model.

Distorted models are widely used, and additional information can be found in the references at the

end of the chapter. References 14 and 15 contain detailed discussions of several practical examples

of distorted fluid flow and hydraulic models.

360 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

Fluids in the News

Old Man River in (large) miniature One of the world’s

largest scale models, a Mississippi River model, resides near

Jackson, Mississippi. It is a detailed, complex model that cov-

ers many acres and replicates the 1,250,000 acre Mississippi

River basin. Built by the Army Corps of Engineers and used

from 1943 to 1973, today it has mostly gone to ruin. As with

many hydraulic models, this is a distorted model, with a hori-

zontal scale of 1 to 2000 and a vertical scale of 1 to 100. One

step along the model river corresponds to one mile along the

river. All essential river basin elements such as geological fea-

tures, levees, and railroad embankments were sculpted by hand

to match the actual contours. The main purpose of the model

was to predict floods. This was done by supplying specific

amounts of water at prescribed locations along the model and

then measuring the water depths up and down the model river.

Because of the length scale, there is a difference in the time

taken by the corresponding model and prototype events. Al-

though it takes days for the actual floodwaters to travel from

Sioux City, Iowa, to Omaha, Nebraska, it would take only min-

utes for the simulated flow in the model.

Models are used to investigate many different types of fluid mechanics problems, and it is diffi-

cult to characterize in a general way all necessary similarity requirements, since each problem is

unique. We can, however, broadly classify many of the problems on the basis of the general na-

ture of the flow and subsequently develop some general characteristics of model designs in each

of these classifications. In the following sections we will consider models for the study of 112flow

through closed conduits, 122flow around immersed bodies, and 132flow with a free surface. Tur-

bomachine models are considered in Chapter 12.

7.9.1 Flow through Closed Conduits

Common examples of this type of flow include pipe flow and flow through valves, fittings, and

metering devices. Although the conduit cross sections are often circular, they could have other

shapes as well and may contain expansions or contractions. Since there are no fluid interfaces

or free surfaces, the dominant forces are inertial and viscous so that the Reynolds number is an

important similarity parameter. For low Mach numbers compressibility effects are

usually negligible for both the flow of liquids or gases. For this class of problems, geometric

similarity between model and prototype must be maintained. Generally the geometric character-

istics can be described by a series of length terms, and where is some par-

ticular length dimension for the system. Such a series of length terms leads to a set of pi terms

of the form

where and so on. In addition to the basic geometry of the system, the roughness of

the internal surface in contact with the fluid may be important. If the average height of surface

roughness elements is defined as then the pi term representing roughness will be This pa-

rameter indicates that for complete geometric similarity, surface roughness would also have to be

scaled. Note that this implies that for length scales less than 1, the model surfaces should be

smoother than those in the prototype since To further complicate matters, the pattern of

roughness elements in model and prototype would have to be similar. These are conditions that are

virtually impossible to satisfy exactly. Fortunately, in some problems the surface roughness plays

⫽ l

Ⲑ

/.e,

i ⫽ 1, 2, . . . ,

⫽

//,/

, /

, . . . , /

1Ma 6 0.32,

7.9 Some Typical Model Studies

Geometric and

Reynolds number

similarity is usually

required for models

involving flow

through closed

conduits.

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 360

a minor role and can be neglected. However, in other problems 1such as turbulent flow through

pipes2roughness can be very important.

It follows from this discussion that for flow in closed conduits at low Mach numbers, any

dependent pi term 1the one that contains the particular variable of interest, such as pressure drop2

can be expressed as

(7.16)

This is a general formulation for this type of problem. The first two pi terms of the right side of

Eq. 7.16 lead to the requirement of geometric similarity so that

This result indicates that the investigator is free to choose a length scale, but once this scale is

selected, all other pertinent lengths must be scaled in the same ratio.

The additional similarity requirement arises from the equality of Reynolds numbers

From this condition the velocity scale is established so that

(7.17)

and the actual value of the velocity scale depends on the viscosity and density scales, as well as

the length scale. Different fluids can be used in model and prototype. However, if the same fluid

is used 1with and 2, then

Thus, which indicates that the fluid velocity in the model will be larger than that in the

prototype for any length scale less than 1. Since length scales are typically much less than unity,

Reynolds number similarity may be difficult to achieve because of the large model velocities re-

quired.

With these similarity requirements satisfied, it follows that the dependent pi term will be equal

in model and prototype. For example, if the dependent variable of interest is the pressure differ-

ential,

between two points along a closed conduit, then the dependent pi term could be

expressed as

The prototype pressure drop would then be obtained from the relationship

so that from a measured pressure differential in the model, the corresponding pressure dif-

ferential for the prototype could be predicted. Note that in general ¢p  ¢p

¢p

¢p 

¢p



¢p

¢p,

 V





 rm

 m



rV/



 l



Dependent pi term  f a

rV/

7.9 Some Typical Model Studies 361

Accurate predic-

tions of flow behav-

ior require the cor-

rect scaling of

velocities.

In some previous examples the pressure differential per unit length, was used. This is appropriate for flow in long pipes or conduits

in which the pressure would vary linearly with distance. However, in the more general situation the pressure may not vary linearly with po-

sition so that it is necessary to consider the pressure differential, as the dependent variable. In this case the distance between pressure

taps is an additional variable 1as well as the distance of one of the taps measured from some reference point within the flow system2.

¢p,

¢p

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 361

362 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

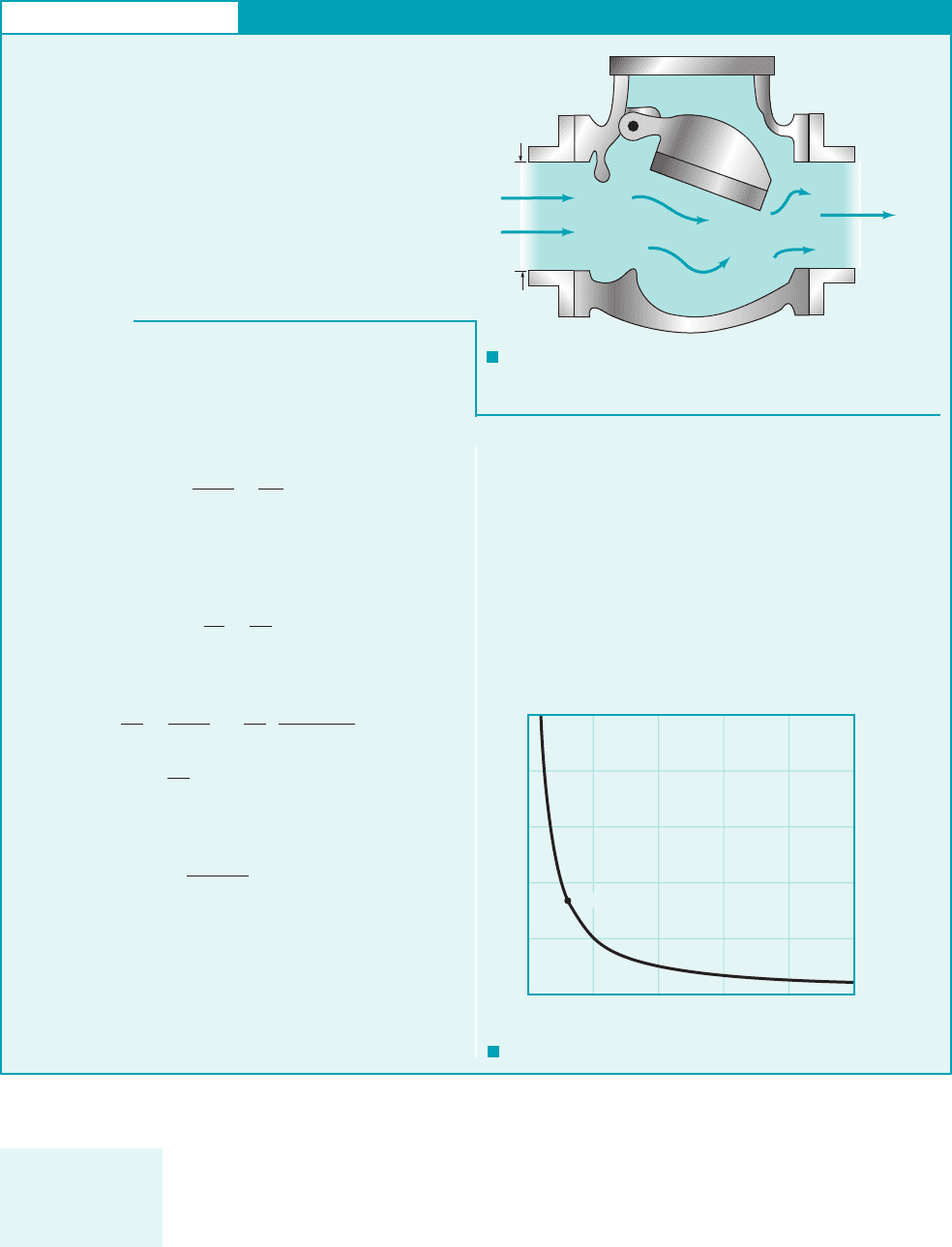
GIVEN Model tests are to be performed to study the flow

through a large check valve having a 2-ft-diameter inlet and

carrying water at a flowrate of 30 cfs as shown in Fig. E7.6a.

The working fluid in the model is water at the same tempera-

ture as that in the prototype. Complete geometric similarity ex-

ists between model and prototype, and the model inlet diameter

is 3 in.

FIND Determine the required flowrate in the model.

OLUTION

Reynolds Number Similarity

For this particular example, , and the correspond-

ing velocity scale is 8 (see Fig. E7.6b). Thus, with the prototype

velocity equal to , the re-

quired model velocity is . Although this is a rela-

tively large velocity, it could be attained in a laboratory facility. It

is to be noted that if we tried to use a smaller model, say one with

the required model velocity is 229 ft兾s, a very high ve-

locity that would be difficult to achieve. These results are indica-

tive of one of the difficulties encountered in maintaining

Reynolds number similarity—the required model velocities may

be impractical to obtain.

D ⫽ 1 in.,

⫽ 76.4 ft

Ⲑ

V ⫽ 130 ft

Ⲑ

4212 ft2

⫽ 9.50 ft

Ⲑ

D ⫽ 0.125

XAMPLE 7.6

To ensure dynamic similarity, the model tests should be run so

that

where V and D correspond to the inlet velocity and diameter, re-

spectively. Since the same fluid is to be used in model and proto-

type, and therefore

The discharge, Q, is equal to VA, where A is the inlet area, so

and for the data given

(Ans)

COMMENT As indicated by the above analysis, to maintain

Reynolds number similarity using the same fluid in model and

prototype, the required velocity scale is inversely proportional to

the length scale, that is, . This strong influence

of the length scale on the velocity scale is shown in Fig. E7.6b.

Ⲑ

V ⫽ 1D

Ⲑ

⫺1

⫽ 3.75 cfs

⫽

Ⲑ

12 ft2

130 ft

Ⲑ

⫽

⫽ a

31p

Ⲑ

42D

31p

Ⲑ

42D

⫽

n ⫽ n

⫽

⫽ Re

F I G U R E E7.6

Q = 30 cfs

(

= ?)

D = 2

(

= 3 in.)

0 0.2 0.4

0.6 0.8 1

(0.125, 8)

F I G U R E E7.6

Two additional points should be made with regard to modeling flows in closed conduits.

First, for large Reynolds numbers, inertial forces are much larger than viscous forces, and in this

case it may be possible to neglect viscous effects. The important practical consequence of this is

that it would not be necessary to maintain Reynolds number similarity between model and proto-

type. However, both model and prototype would have to operate at large Reynolds numbers. Since

we do not know, a priori, what a “large Reynolds number” is, the effect of Reynolds numbers would

In some problems

Reynolds number

similarity may be

relaxed.

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 362

have to be determined from the model. This could be accomplished by varying the model Reynolds

number to determine the range 1if any2over which the dependent pi term ceases to be affected by

changes in Reynolds number.

The second point relates to the possibility of cavitation in flow through closed conduits. For

example, flow through the complex passages that may exist in valves may lead to local regions

of high velocity 1and thus low pressure2, which can cause the fluid to cavitate. If the model is to

be used to study cavitation phenomena, then the vapor pressure, becomes an important vari-

able and an additional similarity requirement such as equality of the cavitation number

is required, where is some reference pressure. The use of models to study cav-

itation is complicated, since it is not fully understood how vapor bubbles form and grow. The ini-

tiation of bubbles seems to be influenced by the microscopic particles that exist in most liquids,

and how this aspect of the problem influences model studies is not clear. Additional details can

be found in Ref. 17.

7.9.2 Flow around Immersed Bodies

Models have been widely used to study the flow characteristics associated with bodies that are

completely immersed in a moving fluid. Examples include flow around aircraft, automobiles,

golf balls, and buildings. 1These types of models are usually tested in wind tunnels as is illus-

trated in Fig. 7.6.2Modeling laws for these problems are similar to those described in the pre-

ceding section; that is, geometric and Reynolds number similarity is required. Since there are

no fluid interfaces, surface tension 1and therefore the Weber number2is not important. Also, grav-

ity will not affect the flow patterns, so the Froude number need not be considered. The Mach

number will be important for high-speed flows in which compressibility becomes an important

factor, but for incompressible fluids 1such as liquids or for gases at relatively low speeds2the

Mach number can be omitted as a similarity requirement. In this case, a general formulation for

these problems is

(7.18)

where is some characteristic length of the system and represents other pertinent lengths,

is the relative roughness of the surface 1or surfaces2, and is the Reynolds number.

Frequently, the dependent variable of interest for this type of problem is the drag, devel-

oped on the body, and in this situation the dependent pi term would usually be expressed in the

form of a drag coefficient, where

The numerical factor, is arbitrary but commonly included, and is usually taken as some rep-

resentative area of the object. Thus, drag studies can be undertaken with the formulation

(7.19)

⫽ C

⫽ f a

rV/

⫽

rV/

Ⲑ

Dependent pi term ⫽ f a

rV/

⫺ p

Ⲑ

7.9 Some Typical Model Studies 363

Geometric and

Reynolds number

similarity is usually

required for models

involving flow

around bodies.

V7.13 Wind engi-

neering models

F I G U R E 7.6 Model of the National

Bank of Commerce, San Antonio, Texas, for measure-

ment of peak, rms, and mean pressure distributions.

The model is located in a long-test-section, meteoro-

logical wind tunnel. (Photograph courtesy of Cermak

Peterka Petersen, Inc.)

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 363

It is clear from Eq. 7.19 that geometric similarity

as well as Reynolds number similarity

must be maintained. If these conditions are met, then

Measurements of model drag, can then be used to predict the corresponding drag, on the

prototype from this relationship.

As was discussed in the previous section, one of the common difficulties with models is re-

lated to the Reynolds number similarity requirement which establishes the model velocity as

(7.20)

(7.21)

where is the ratio of kinematic viscosities. If the same fluid is used for model and prototype

so that then

and, therefore, the required model velocity will be higher than the prototype velocity for

greater than 1. Since this ratio is often relatively large, the required value of may be large. For

example, for a length scale, and a prototype velocity of 50 mph, the required model velocity is

500 mph. This is a value that is unreasonably high to achieve with liquids, and for gas flows this

would be in the range where compressibility would be important in the model 1but not in the

prototype2.

As an alternative, we see from Eq. 7.21 that could be reduced by using a different fluid

in the model such that For example, the ratio of the kinematic viscosity of water to that

of air is approximately so that if the prototype fluid were air, tests might be run on the model

using water. This would reduce the required model velocity, but it still may be difficult to achieve

the necessary velocity in a suitable test facility, such as a water tunnel.

Another possibility for wind tunnel tests would be to increase the air pressure in the tunnel

so that thus reducing the required model velocity as specified by Eq. 7.20. Fluid viscos-

ity is not strongly influenced by pressure. Although pressurized tunnels have been used, they are

obviously more complicated and expensive.

The required model velocity can also be reduced if the length scale is modest; that is, the

model is relatively large. For wind tunnel testing, this requires a large test section which greatly

increases the cost of the facility. However, large wind tunnels suitable for testing very large mod-

els 1or prototypes2are in use. One such tunnel, located at the NASA Ames Research Center, Mof-

fett Field, California, has a test section that is 40 ft by 80 ft and can accommodate test speeds to

345 mph. Such a large and expensive test facility is obviously not feasible for university or indus-

trial laboratories, so most model testing has to be accomplished with relatively small models.

7 r,

Ⲑ

n 6 1.

Ⲑ

⫽

⫽ n,

Ⲑ

⫽

d,d

d ⫽

⫽

rV/

⫽

364 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

For flow around

bodies, drag is of-

ten the dependent

variable of interest.

V7.14 Model air-

plane test in water

V7.15 Large scale

wind tunnel

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 364

Fortunately, in many situations the flow characteristics are not strongly influenced by the

Reynolds number over the operating range of interest. In these cases we can avoid the rather strin-

gent similarity requirement of matching Reynolds numbers. To illustrate this point, consider the

variation in the drag coefficient with the Reynolds number for a smooth sphere of diameter d placed

in a uniform stream with approach velocity, V. Some typical data are shown in Fig. 7.7. We ob-

serve that for Reynolds numbers between approximately and the drag coefficient is

relatively constant and does not strongly depend on the specific value of the Reynolds number.

Thus, exact Reynolds number similarity is not required in this range. For other geometric shapes

we would typically find that for high Reynolds numbers, inertial forces are dominant 1rather than

viscous forces2, and the drag is essentially independent of the Reynolds number.

2  10

7.9 Some Typical Model Studies 365

GIVEN The drag on the airplane shown in Fig. E7.7 cruising

at 240 mph in standard air is to be determined from tests on a 1:10

scale model placed in a pressurized wind tunnel. To minimize

compressibility effects, the air speed in the wind tunnel is also to

be 240 mph.

FIND Determine

(a) the required air pressure in the tunnel (assuming the same

air temperature for model and prototype) and

OLUTION

F I G U R E E7.7

Model Design Conditions and Predicted Prototype Performance

for constant temperature Therefore, the wind tunnel

would need to be pressurized so that

Since the prototype operates at standard atmospheric pressure,

the required pressure in the wind tunnel is 10 atmospheres or

(Ans)

COMMENT Thus, we see that a high pressure would be re-

quired and this could not be achieved easily or inexpensively. How-

ever, under these conditions, Reynolds similarity would be attained.

(b) The drag could be obtained from Eq. 7.19 so that

Thus, for a drag of 1 lb on the model the corresponding drag on

the prototype is

(Ans)

d  10 lb

 10d

 a

b 112

1102

d 



 147 psia

 10 114.7 psia2

 10

1T  T

V = 240 mph

XAMPLE 7.7

(a) From Eq. 7.19 it follows that drag can be predicted from a

geometrically similar model if the Reynolds numbers in model

and prototype are the same. Thus,

For this example, and so that

and therefore

This result shows that the same fluid with and

cannot be used if Reynolds number similarity is to be maintained.

One possibility is to pressurize the wind tunnel to increase the

density of the air. We assume that an increase in pressure does not

significantly change the viscosity so that the required increase in

density is given by the relationship

For an ideal gas, so that



p  rRT

 10

 mr

 r

 10



1121102





/ 

 V



rV/

(b) the drag on the prototype corresponding to a measured force

of 1 lb on the model.

V7.16 Wind tunnel

train model

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 365

Another interesting point to note from Fig. 7.7 is the rather abrupt drop in the drag coeffi-

cient near a Reynolds number of As is discussed in Section 9.3.3, this is due to a change

in the flow conditions near the surface of the sphere. These changes are influenced by the surface

roughness and, in fact, the drag coefficient for a sphere with a “rougher” surface will generally be

less than that of the smooth sphere for high Reynolds number. For example, the dimples on a

golf ball are used to reduce the drag over that which would occur for a smooth golf ball. Al-

though this is undoubtedly of great interest to the avid golfer, it is also important to engineers

responsible for fluid-flow models, since it does emphasize the potential importance of the sur-

face roughness. However, for bodies that are sufficiently angular with sharp corners, the actual

surface roughness is likely to play a secondary role compared with the main geometric features

of the body.

One final note with regard to Fig. 7.7 concerns the interpretation of experimental data when

plotting pi terms. For example, if , , and d remain constant, then an increase in Re comes from

an increase in V. Intuitively, it would seem in general that if V increases, the drag would increase.

However, as shown in the figure, the drag coefficient generally decreases with increasing Re. When

interpreting data, one needs to be aware if the variables are nondimensional. In this case, the phys-

ical drag force is proportional to the drag coefficient times the velocity squared. Thus, as shown

by the figure in the margin, the drag force does, as expected, increase with increasing velocity. The

exception occurs in the Reynolds number range where the drag coeffi-

cient decreases dramatically with increasing Reynolds number (see Fig. 7.7). This phenomena is

discussed in Section 9.3.

For problems involving high velocities in which the Mach number is greater than about 0.3,

the influence of compressibility, and therefore the Mach number 1or Cauchy number2, becomes sig-

nificant. In this case complete similarity requires not only geometric and Reynolds number simi-

larity but also Mach number similarity so that

(7.22)

This similarity requirement, when combined with that for Reynolds number similarity 1Eq. 7.212,

yields

(7.23)



2  10

6 Re 6 4  10

3  10

366 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

At high Reynolds

numbers the drag is

often essentially in-

dependent of the

Reynolds number.

Drag coefficient, C

0.06

2 468 2 468 2 468 2 468 2 468 2 468 2 468

–1

Reynolds number, Re =

____

0.08

0.1

0.2

0.4

0.6

0.8

100

200

400

F I G U R E 7.7 The effect of Reynolds number on the drag coefficient, C

, for a

smooth sphere with where A is the projected area of sphere, (Data from

Ref. 16, used by permission.)



4.C

 d



ARV

ᑞ

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 366