Neamen D. Microelectronics: Circuit Analysis and Design

Подождите немного. Документ загружается.

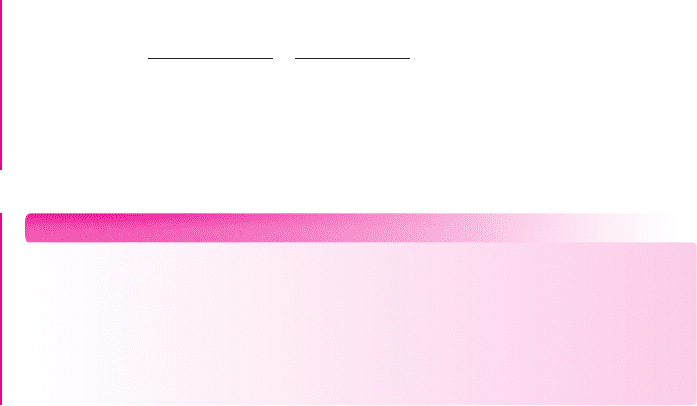
488 Part 1 Semiconductor Devices and Basic Applications

Therefore,

max

(69.6)(1.44)(2)

(0.1 + 6.775)



8.084

8.084 + 41.84



= 4.72

Comment: The coupling capacitor produces a high-pass network. In this circuit, if

the signal frequency is approximately two octaves above the corner frequency, the

coupling capacitor acts as a short circuit.

EXERCISE PROBLEM

Ex 7.3: For the circuit shown in Figure 7.21(a), the parameters are:

= 3

= 0, R

= 110



= 42 k

= 0.5k

= 7k

, and

0.47 μ

F. The transistor parameters are

β = 150

(on) = 0.7

V, and

=∞

(a) Determine the expression for and the value of the time constant

. (b) Deter-

mine the corner frequency and midband voltage gain. (Ans. (a)

= R

10.87

ms; (b)

= 14.6

Hz,

=−10.84)

Time Constant Technique: In general, we do not need to derive the complete cir-

cuit transfer function including capacitance effects in order to complete the Bode plot

and determine the frequency response. By looking at a circuit with, initially, only one

capacitor, we can determine if the ampliﬁer is a low-pass or high-pass circuit. We can

then specify the Bode plot if we know the time constant and the maximum midband

gain. The time constant determines the corner frequency. The midband gain is found

in the usual way when capacitances are eliminated from the circuit.

This time constant technique yields good results when all poles are real, as will

be the case in this chapter. In addition, this technique does not determine the corner

frequencies due to system zeros. The major beneﬁt of using the time constant ap-

proach is that it gives information about which circuit elements affect the

−3

dB fre-

quency of the circuit. A coupling capacitor produces a high-pass network, so the form

of the Bode plot will be the same as that shown in Figure 7.5. Also, the maximum

gain is determined when the coupling capacitor acts as a short circuit, as was as-

sumed in Chapters 4 and 6.

The time constant for the circuit is a function of the equivalent resistance seen

by the capacitor. The small-signal equivalent circuit is shown in Figure 7.21(b). If we

set the independent voltage source equal to zero, the equivalent resistance seen by

the coupling capacitor

is (

+ R

). The time constant is then

= (R

+ R

(7.38)

This is the same as Equation (7.35), which was determined by using a current–

voltage analysis.

Output Coupling Capacitor: Common-Source Circuit

Figure 7.22(a) shows a common-source MOSFET ampliﬁer. We assume that the re-

sistance of the signal generator is much less than R

and can therefore be neglected.

In this case, the output signal is connected to the load through a coupling capacitor.

The small-signal equivalent circuit, assuming r

is inﬁnite, is shown in Fig-

ure 7.22(b). The maximum output voltage, assuming C

is a short circuit, is

max

= g

R

)

(7.39)

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 488 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

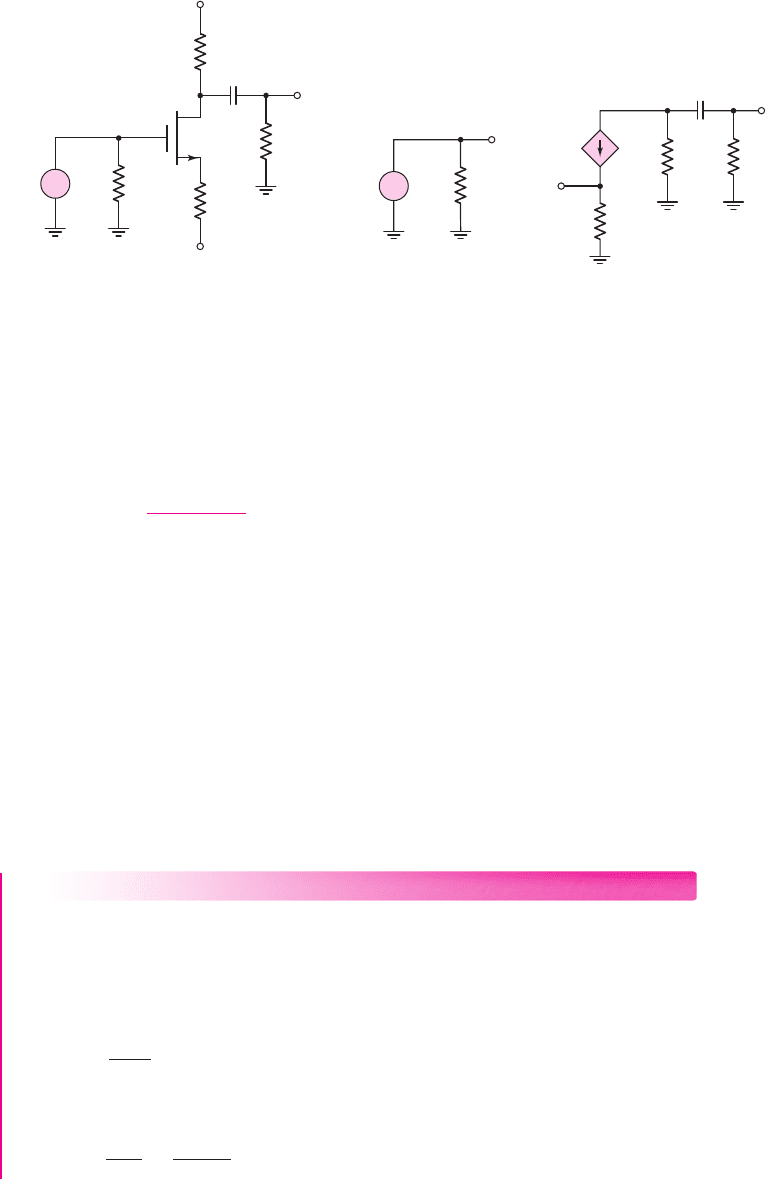
Chapter 7 Frequency Response 489

and the input voltage can be written as

= V

+ g

(7.40)

Therefore, the maximum small-signal gain is

max

R

)

1 + g

(7.41)

Even though the coupling capacitor is in the output portion of the circuit, the

Bode plot will still be that of a high-pass network, as shown in Figure 7.5. Using the

time constant technique to determine the corner frequency will substantially simplify

the circuit analysis, since we do not speciﬁcally need to determine the transfer

function for the frequency response.

The time constant is a function of the effective resistance seen by capacitor C

which is determined by setting all independent sources equal to zero. Since

= 0

then

= 0

and

= 0

, and the effective resistance seen by C

is (

+ R

The time constant is then

= (R

+ R

(7.42)

and the corner frequency is

= 1/2πτ

DESIGN EXAMPLE 7.4

Objective: The circuit in Figure 7.22(a) is to be used as a simple audio ampliﬁer.

Design the circuit such that the lower corner frequency is

= 20

Hz.

Solution: The corner frequency can be written in terms of the time constant, as

follows:

2πτ

The time constant is then

2π f

2π(20)

⇒ 7.96 ms

(a) (b)

50 kΩ

+5 V

–5 V

5 kΩ

= 6.7 kΩ

10 kΩ

–

50 kΩ

–

10 kΩ

6.7 kΩ

5 kΩ

–

Figure 7.22 (a) Common-source circuit with output coupling capacitor and (b) small-signal

equivalent circuit

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 489 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

490 Part 1 Semiconductor Devices and Basic Applications

EXERCISE PROBLEM

Ex 7.4: Consider the circuit shown in Figure 7.22(a). The bias voltages are

changed to

= 3

V and

−

=−3

V. Other circuit parameters are

= 20 k

and

= 100 k

. The transistor parameters are

= 0.4V, K

= 100 μA/V

and

λ = 0

. (a) Design the circuit such that

= 250 μ

A and

DSQ

= 1.7

(b) If

= 0.7 μ

F, determine the corner frequency. (Ans. (a)

= 4.08 k

= 13.1k

; (b)

= 6.87

Hz)

Output Coupling Capacitor: Emitter-Follower Circuit: An emitter follower with

a coupling capacitor in the output portion of the circuit is shown in Figure 7.23(a).

We assume that coupling capacitor C

, which is part of the original emitter follower,

is very large, and that it acts as a short circuit to the input signal.

The small-signal equivalent circuit, including the small-signal transistor resis-

tance r

, is shown in Figure 7.23(b). The equivalent resistance seen by the coupling

capacitor C

is [

+ R

], and the time constant is

= [R

+ R

(7.43)

where R

is the output resistance as deﬁned in Figure 7.23(b).As shown in Chapter 6,

the output resistance is

= R

r





+(R

R

)]

1 + β



(7.44)

= 0.5 kΩ

= 100 kΩ

+10 V

–10 V

10 kΩ

–

= 0.5 kΩ

100 kΩ

(a) (b)

–

→ ∞

Figure 7.23 (a) Emitter-follower circuit with output coupling capacitor and (b) small-signal

equivalent circuit

Therefore, from Equation (7.42) the coupling capacitance is

+ R

7.96 × 10

−3

6.7 × 10

+10 ×10

= 4.77 ×10

−7

= 0.477 μF

Comment: Using the time constant technique to ﬁnd the corner frequency is sub-

stantially easier than using the circuit analysis approach.

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 490 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

Chapter 7 Frequency Response 491

If we combine Equations (7.44) and (7.43), the time constant expression

becomes fairly complicated. However, the current–voltage analysis of this circuit

including C

is even more cumbersome. The time constant technique again simpli-

ﬁes the analysis substantially.

EXAMPLE 7.5

Objective: Determine the 3 dB frequency of an emitter-follower ampliﬁer circuit

with an output coupling capacitor.

Consider the circuit shown in Figure 7.23(a) with transistor parameters

β = 100

(on) = 0.7

V, and

= 120

V. The output coupling capacitance is

= 1 μ

Solution: A dc analysis shows that

= 0.838

mA. Therefore, the small-signal

parameters are:

= 3.10 k

= 32.2

mA/V, and

= 143 k

From Equation (7.44), the output resistance R

of the emitter follower is

= R

r





+(R

R

)]

1 + β



= 10143



[3.10 + (0.5100)]

101



= 101430.0356 k

∼

35.5 

From Equation (7.43), the time constant is

= [R

+ R

= [35.5 +10

](10

−6

)

∼

1 × 10

−2

The 3 dB frequency is then

2πτ

2π(10

−2

)

= 15.9Hz

Comment: Determining the 3 dB or corner frequency is very direct with the time

constant technique.

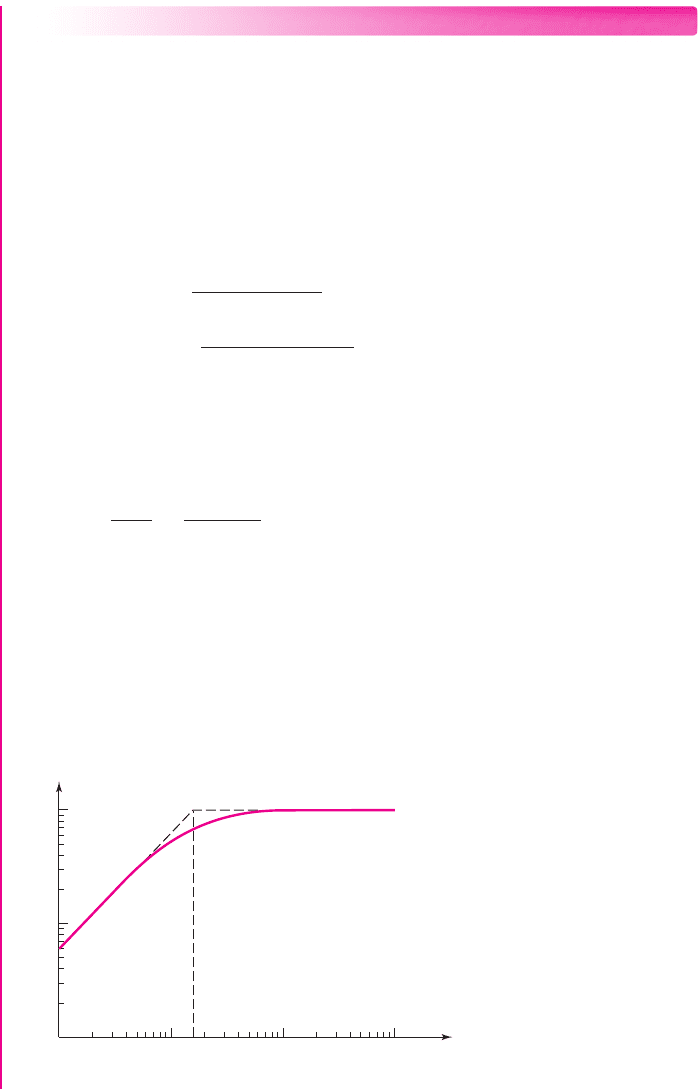
Computer Veriﬁcation: Based on PSpice, analysis, Figure 7.24 is a Bode plot of the

voltage gain magnitude of the emitter-follower circuit shown in Figure 7.23(a). The

corner frequency is essentially identical to that obtained by the time constant tech-

nique. Also, the asymptotic value of the small-signal voltage gain is

= 0.988

,as

expected for an emitter-follower circuit.

f (Hz)

1 10 100 1000

0.01

0.1

1.0

Figure 7.24 PSpice analysis results for the emitter-follower circuit in Figure 7.23(a)

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 491 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

492 Part 1 Semiconductor Devices and Basic Applications

EXERCISE PROBLEM

Ex 7.5: For the emitter-follower circuit shown in Figure 7.23(a), determine the

required value of C

to yield a corner frequency of 10 Hz. (Ans.

= 1.59 μ

Problem-Solving Technique: Bode Plot of Gain Magnitude

1. For a particular capacitor in a circuit, determine whether the capacitor is pro-

ducing a low-pass or high-pass circuit. From this, sketch the general shape of

the Bode plot.

2. The corner frequency is found from

f = 1/2 πτ

where the time constant is

τ = R

. The equivalent resistance R

is the equivalent resistance seen by

the capacitor.

3. The maximum gain magnitude is the midband gain. Coupling and bypass ca-

pacitors act as short circuits and load capacitors act as open circuits.

Load Capacitor Effects

An ampliﬁer output may be connected to a load or to the input or another ampliﬁer.

The model of the load circuit input impedance is generally a capacitance in parallel

with a resistance. In addition, there is a parasitic capacitance between ground and the

line that connects the ampliﬁer output to the load circuit.

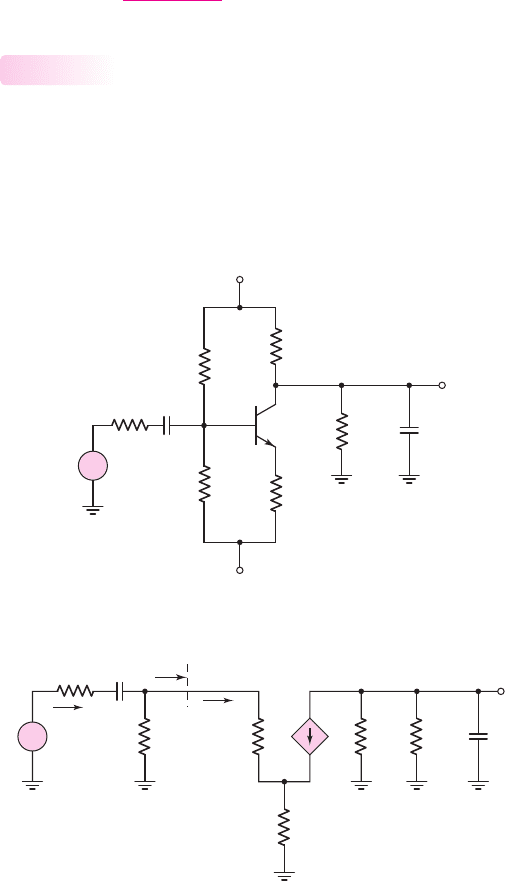
Figure 7.25(a) shows a MOSFET common-source ampliﬁer with a load resis-

tance R

and a load capacitance C

connected to the output, and Figure 7.25(b) shows

the small-signal equivalent circuit. The transistor small-signal output resistance r

assumed to be inﬁnite. This circuit conﬁguration is essentially the same as that in

Figure 7.3, which is a low-pass network. At high frequencies, the impedance of C

decreases and acts as a shunt between the output and ground, and the output voltage

tends toward zero. The Bode plot is similar to that shown in Figure 7.8, with an upper

corner frequency and a maximum gain asymptote.

7.3.2

200 kΩ

+5 V

–5 V

200 kΩ

–

(a) (b)

–

Figure 7.25 (a) MOSFET common-source circuit with a load capacitor and (b) small-signal

equivalent circuit

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 492 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

Chapter 7 Frequency Response 493

The equivalent resistance seen by the load capacitor C

R

. Since we set

= 0

, then

= 0

, which means that the dependent current source does not

affect the equivalent resistance.

The time constant for this circuit is

= (R

R

(7.45)

The maximum gain asymptote, which is found by assuming C

is an open

circuit, is

max

R

)

1 + g

(7.46)

Coupling and Load Capacitors

A circuit with both a coupling capacitor and a load capacitor is shown in Fig-

ure 7.26(a). Since the values of the coupling capacitance and load capacitance differ

by orders of magnitude, the corner frequencies are far apart and can be treated

separately as discussed previously. The small-signal equivalent circuit is shown in

Figure 7.26(b), assuming the transistor small-signal resistance r

is inﬁnite.

7.3.3

15 pF

5.7 kΩ

40 kΩ

= 0.1 kΩ

+5 V

–5 V

10 kΩ

0.5 kΩ

= 5 kΩ

–

(a)

(b)

5 kΩ

10 kΩ

= 0.1 kΩ

⎪⎪R

5 kΩ

–

= 0.5 kΩ

15 pF

–

Figure 7.26 (a) Circuit with both a coupling and a load capacitor and (b) small-signal

equivalent circuit

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 493 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

494 Part 1 Semiconductor Devices and Basic Applications

The Bode plot of the voltage gain magnitude is similar to that shown in Figure

7.11. The lower corner frequency f

is given by

2πτ

(7.47)

where

is the time constant associated with the coupling capacitor C

, and the

upper corner frequency f

is given by

2πτ

(7.48)

where

is the time constant associated with the load capacitor C

. It should be

emphasized that Equations (7.47) and (7.48) are valid only as long as the two corner

frequencies are far apart.

Using the small-signal equivalent circuit in Figure 7.26(b), we set the signal

source equal to zero to ﬁnd the equivalent resistance associated with the coupling ca-

pacitor. The related time constant is

= [R

+(R

R

(7.49)

where

= r

+(1 +β)R

(7.50)

Similarly, the time constant related to C

= (R

R

(7.51)

Since the two corner frequencies are far apart, the gain will reach a maximum

value in the frequency range between f

and f

, which is the midband. We can calcu-

late the midband gain by assuming that the coupling capacitor is a short circuit and

the load capacitor is an open circuit.

Using the analysis techniques from the last chapter, we ﬁnd the magnitude of the

midband gain as follows:



= g

R

)



R

) + R



+(R

R

)]



(7.52)

EXAMPLE 7.6

Objective: Determine the midband gain, corner frequencies, and bandwidth of a

circuit containing both a coupling capacitor and a load capacitor.

Consider the circuit shownin Figure 7.26(a) with transistor parameters

(on) =

0.7 V,

β = 100

, and

=∞

Solution: The dc analysis of this circuit yields a quiescent collector current of

= 0.99

mA. The small-signal parameters are

= 38.08

mA/V,

= 2.626 k

and

=∞

The input resistance R

is therefore

= r

+(1 +β)R

= 2.63 +(101)(0.5) = 53.1k

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 494 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

Chapter 7 Frequency Response 495

From Equation (7.52), the midband gain is

max



max

= g

R

)



R

) + R



+(R

R

)]



= (38.08)(2.626)(510)



405.7

(405.7) + 53.1



[0.1 + (405.753.1)]





max

= 6.14

The time constant

= (R

+ R

R

= (0.1 ×10

+(5.7 ×10

)(40 × 10

)(53.1 × 10

))(10 × 10

−6

)

= 4.67 ×10

−2

s ⇒ 46.6ms

and the time constant

= (R

R

= ((5 ×10

)(10 × 10

))(15 × 10

−12

) = 5 ×10

−8

= 50 ns

The lower corner frequency is

2πτ

2π(46.6 ×10

−3

)

= 3.42 Hz

and the upper corner frequency is

2πτ

2π(50 ×10

−9

)

⇒ 3.18 MHz

Finally, the bandwidth is

= f

− f

= 3.18 MHz − 3.4Hz

∼

3.18 MHz

Comment: The two corner frequencies differ by approximately six orders of magni-

tude; therefore, considering one capacitor at a time is a valid approach.

EXERCISE PROBLEM

Ex 7.6: Consider the circuit in Figure 7.26(a). The load resistance value is

changed to

= 5k

, and the capacitor values are changed to

= 5

pF and

= 5 μ

F. Other circuit and transistor parameters are the same as given in Ex-

ample 7.6. (a) Determine the new values of the collector current and small-signal

hybrid-pi parameters. (b) Determine the value of midband voltage gain. (c) Find

the corner frequencies of the circuit. (Ans. (a)

= 0.986

mA, (b)

=−4.60

(c)

= 6.82

Hz,

= 12.7

MHz)

A ﬁgure of merit for an ampliﬁer is the gain–bandwidth product.Assuming the

corner frequencies are far apart, the bandwidth is

= f

− f

∼

(7.53)

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 495 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

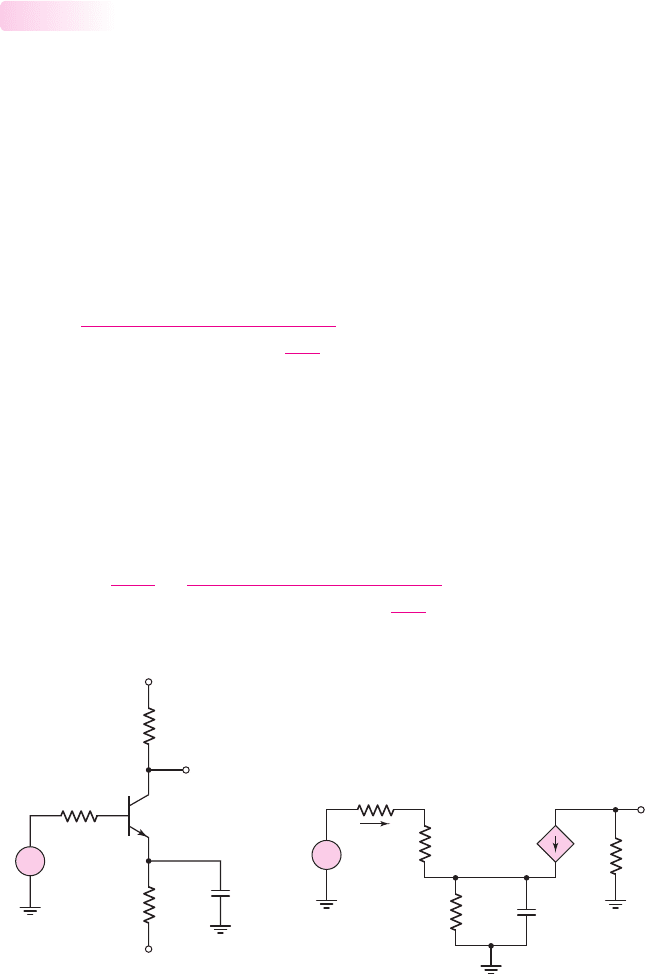
496 Part 1 Semiconductor Devices and Basic Applications

Figure 7.27

(a) Circuit with emitter bypass capacitor and (b) small-signal equivalent circuit

and the maximum gain is

max

. The gain–bandwidth product is therefore

GB =|A

max

· f

(7.54)

Later we will show that, for a given load capacitance, this product is essentially a

constant. We will also describe how trade-offs must be made between gain and band-

width in ampliﬁer design.

Bypass Capacitor Effects

In bipolar and FET discrete ampliﬁers, emitter and source bypass capacitors are often

included so that emitter and source resistors can be used to stabilize the Q-point with-

out sacriﬁcing the small-signal gain. The bypass capacitors are assumed to act as

short circuits at the signal frequency. However, to guide us in choosing a bypass

capacitor, we must determine the circuit response in the frequency range where these

capacitors are neither open nor short circuits.

Figure 7.27(a) shows a common-emitter circuit with an emitter bypass capacitor.

The small-signal equivalent circuit is shown in Figure 7.27(b). We can ﬁnd the small-

signal voltage gain as a function of frequency. Using the impedance reﬂection rule,

the small-signal input current is

+(1 +β)







(7.55)

The total impedance in the emitter is multiplied by the factor

(1 + β)

. The control

voltage is

= I

(7.56)

and the output voltage is

=−g

(7.57)

Combining equations produces the small-signal voltage gain, as follows:

(s) =

(s)

−g

+(1 +β)







(7.58)

7.3.4

(a)

(b)

–

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 496 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

Chapter 7 Frequency Response 497

Expanding the parallel combination of R

and 1/sC

and rearranging terms, we ﬁnd

−g

+(1 +β)R

]

(1 + sR

)



1 +

+(1 +β)R

]



(7.59)

Equation (7.59) can be written in terms of time constants as

−g

+(1 +β)R

]



1 + sτ



(7.60)

The form of this transfer function is somewhat different from what we have pre-

viously encountered in that we have both a zero and a pole.

The Bode plot of the voltage gain magnitude has two limiting horizontal

asymptotes. If we set

s = jω

, we can then consider the limit as

ω → 0

and the limit

ω →∞

. For

ω → 0

, C

acts as an open circuit; for

ω →∞

, C

acts as a short

circuit. From Equation (7.59), we have

ω→0

+(1 +β)R

]

(7.61(a))

and

ω→∞

(7.61(b))

From these results, we see that for

ω → 0

, R

is included in the gain expression, and

for

ω →∞

, R

is not part of the gain expression, since it has been effectively

shorted out by C

If we assume that the time constants

and

in Equation (7.60) differ sub-

stantially in magnitude, then the corner frequency due to

2πτ

(7.62(a))

and the corner frequency due to

2πτ

(7.62(b))

The resulting Bode plot of the voltage gain magnitude is shown in Figure 7.28.

→ 0

→ ∞

Figure 7.28 Bode plot of the voltage gain magnitude for the circuit with an emitter bypass

capacitor

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 497 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07: