Neamen D. Microelectronics: Circuit Analysis and Design

Подождите немного. Документ загружается.

468 Part 1 Semiconductor Devices and Basic Applications

6.82 For the circuit shown in Figure 6.43, use the circuit and transistor parame-

ters described in Example 6.9. (a) Calculate the average power dissipated

in the transistor,

, and

, for

= 0

. (b) Determine the maximum sig-

nal power that can be delivered to

. What are the signal powers dissipated

and

, and what is the average power dissipated in the transistor in

this case?

6.83 For the circuit shown in Figure 6.57, the transistor parameters are

β = 100

and

= 100

V, and the source resistor is

= 0

. Determine the maxi-

mum undistorted signal power that can be delivered to

if: (a)

1k

, and (b)

= 10 k

6.84 Consider the circuit shown in Figure 6.64 with parameters given in Exer-

cise TYU 6.14. (a) Calculate the average power dissipated in the transistor

and

, for

= 0

. (b) Determine the maximum undistorted signal power

that can be delivered to

, and the resulting average power dissipated in

the transistor and

COMPUTER SIMULATION PROBLEMS

6.85 (a) Using a computer simulation, verify the results of Exercise Ex 6.5.

(b) Repeat part (a) for Early voltages of (i)

= 100

V and (ii)

= 50

6.86 (a) Using a computer simulation, verify the results of Exercise TYU 6.7.

(b) Repeat part (a) for an Early voltage of

= 50

6.87 Using a computer simulation, verify the results of Example 6.10.

6.88 Using a computer simulation, verify the results of Exercise Ex 6.15 for the

multitransistor ampliﬁer.

DESIGN PROBLEMS

[Note: Each design should be correlated with a computer simulation.]

*D6.89 Design a common-emitter ampliﬁer with the general conﬁguration shown in

Figure 6.39 except with a pnp transistor. The magnitude of the small-signal

voltage gain should be

|=50

while driving a load

= 10



. Bias

the circuit at

±3.3

*D6.90 Consider the circuit in Figure 6.20. Let

= 5

= 10



β = 120

and

=∞

. Design the circuit such that the small-signal current gain is

= 20

and such that the maximum undistorted swing in the output volt-

age is achieved.

*D6.91 A microphone puts out a peak voltage of 2 mV and has an output resistance

of 5 k



. Design an ampliﬁer system to drive a 24



speaker, producing

0.5 W of signal power. Assume a current gain of

β = 50

for all available

transistors. Specify the current and power ratings of the transistors.

*D6.92 Redesign the two-stage ampliﬁer in Figure 6.66 such that the voltage gain

of each stage is

= A

=−50

. Assume transistor current gains of

npn

= 150

and

pnp

= 110

. The total power dissipated in the circuit should

be limited to 25 mW.

nea80644_ch06_369-468.qxd 06/13/2009 08:21 PM Page 468 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-06:

Chapter

469

Thus far in our linear ampliﬁer analyses, we have assumed that coupling capacitors

and bypass capacitors act as short circuits to the signal voltages and open circuits to

dc voltages. However, capacitors do not change instantaneously from a short circuit

to an open circuit as the frequency approaches zero. We have also assumed that tran-

sistors are ideal in that output signals respond instantaneously to input signals. How-

ever, there are internal capacitances in both the bipolar transistor and ﬁeld-effect

transistor that affect the frequency response. The major goal of this chapter is to de-

termine the frequency response of ampliﬁer circuits due to circuit capacitors and

transistor capacitances.

PREVIEW

In this chapter, we will:

• Discuss the general frequency response characteristics of ampliﬁers.

• Derive the system transfer functions of two simple R–C circuits, develop the

Bode plots for the magnitude and phase of the transfer functions, and become

familiar with sketching the Bode diagrams.

• Analyze the frequency response of transistor circuits with capacitors.

• Determine the frequency response of the bipolar transistor, and determine the

Miller effect and Miller capacitance.

• Determine the frequency response of the MOS transistor, and determine the

Miller effect and Miller capacitance.

• Determine the high-frequency response of basic transistor circuit conﬁgura-

tions including the cascode circuit.

• As an application, design a two-stage BJT ampliﬁer with coupling capacitors

such that the 3 dB frequencies associated with each stage are equal.

Frequency Response

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 469 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

470 Part 1 Semiconductor Devices and Basic Applications

In many references, the gain is plotted as a function of the radian frequency

. All curves in this chapter,

for consistency, will be plotted as a function of cyclical frequency f (Hz). We note that

ω = 2π

. The

ampliﬁer gain is also plotted in terms of decibels (dB), where

|A|

= 20 log

|A|

7.1 AMPLIFIER FREQUENCY RESPONSE

Objective: • Discuss the general frequency response characteristics

of ampliﬁers.

All ampliﬁer gain factors are functions of signal frequency. These gain factors in-

clude voltage, current, transconductance, and transresistance. Up to this point, we

have assumed that the signal frequency is high enough that coupling and bypass ca-

pacitors can be treated as short circuits and, at the same time, we have assumed that

the signal frequency is low enough that parasitic, load, and transistor capacitances

can be treated as open circuits. In this chapter, we consider the ampliﬁer response

over the entire frequency range.

In general, an ampliﬁer gain factor versus frequency will resemble that shown in

Figure 7.1.

Both the gain factor and frequency are plotted on logarithmic scales (the

gain factor in terms of decibels). Three frequency ranges, low, midband, and high,

are indicated. In the low-frequency range,

f < f

, the gain decreases as the fre-

quency decreases because of coupling and bypass capacitor effects. In the high-

frequency range,

f > f

, stray capacitance and transistor capacitance effects cause

the gain to decrease as the frequency increases. The midband range is the region

where coupling and bypass capacitors act as short circuits, and stray and transistor

capacitances act as open circuits. In this region, the gain is almost a constant. As we

will show, the gain at

f = f

and at

f = f

is 3 dB less than the maximum midband

gain. The bandwidth of the ampliﬁer (in Hz) is deﬁned as

= f

− f

|A( jf )|

f (Hz)

(lo

scale)

Low-frequency

range

Midband

High-frequency

range

3 dB 3 dB

Figure 7.1 Ampliﬁer gain versus frequency

For an audio ampliﬁer, for example, signal frequencies in the range of 20 Hz

f < 20

kHz need to be ampliﬁed equally so as to reproduce the sound as accu-

rately as possible. Therefore, in the design of a good audio ampliﬁer, the frequency

must be designed to be less than 20 Hz and

must be designed to be greater than

20 kHz.

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 470 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

Chapter 7 Frequency Response 471

Equivalent Circuits

Each capacitor in a circuit is important at only one end of the frequency spectrum.

For this reason, we can develop speciﬁc equivalent circuits that apply to the low-

frequency range, to midband, and to the high-frequency range.

Midband Range

The equivalent circuits used for calculations in the midband range are the same as

those considered up to this point in the text. As already mentioned, the coupling and

bypass capacitors in this region are treated as short circuits. The stray and transistor

capacitances are treated as open circuits. In this frequency range, there are no capac-

itances in the equivalent circuit. These circuits are referred to as midband equivalent

circuits.

Low-Frequency Range

In this frequency range, we use a low-frequency equivalent circuit. In this region,

coupling and bypass capacitors must be included in the equivalent circuit and in the

ampliﬁcation factor equations. The stray and transistor capacitances are treated as

open circuits. The mathematical expressions obtained for the ampliﬁcation factor in

this frequency range must approach the midband results as f approaches the midband

frequency range, since in this limit the capacitors approach short-circuit conditions.

High-Frequency Range

In the high-frequency range, we use a high-frequency equivalent circuit. In this re-

gion, coupling and bypass capacitors are treated as short circuits. The transistor and

any parasitic or load capacitances must be taken into account in this equivalent

circuit. The mathematical expressions obtained for the ampliﬁcation factor in this

frequency range must approach the midband results as f approaches the midband fre-

quency range, since in this limit the capacitors approach open-circuit conditions.

Frequency Response Analysis

Using the three equivalent circuits just considered rather than a complete circuit is an

approximation technique that produces useful hand-analysis results while avoiding

complex transfer functions. This technique is valid if there is a large separation

between f

and f

, that is

 f

. This condition is satisﬁed in many electronic cir-

cuits that we will consider.

Computer simulations, such as PSpice, can take into account all capacitances

and can produce frequency response curves that are more accurate than the hand-

analysis results. However, the computer results do not provide any physical insight

into a particular result and hence do not provide any suggestions as to design changes

that can be made to improve a particular frequency response. A hand analysis can

provide insight into the “whys and wherefores” of a particular response. This basic

understanding can then lead to a better circuit design.

In the next section, we introduce two simple circuits to begin our frequency

analysis study. We initially derive the mathematical expressions relating output volt-

age to input voltage (transfer function) as a function of signal frequency. From these

functions, we can develop the response curves. The two frequency response curves

give the magnitude of the transfer function versus frequency and the phase of the

7.1.2

7.1.1

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 471 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

472 Part 1 Semiconductor Devices and Basic Applications

transfer function versus frequency. The phase response relates the phase of the output

signal to the phase of the input signal.

We will then develop a technique by which we can easily sketch the frequency

response curves without resorting to a full analysis of the transfer function. This sim-

pliﬁed approach will lead to a general understanding of the frequency response of

electronic circuits. We will then rely on a computer simulation to provide more

detailed calculations when required.

7.2 SYSTEM TRANSFER FUNCTIONS

Objective: • Derive the system transfer functions of two circuits, de-

velop the Bode diagrams of the magnitude and phase of the transfer

functions, and become familiar with sketching the Bode diagrams.

The frequency response of a circuit is usually determined by using the complex fre-

quency s. Each capacitor is represented by its complex impedance, 1/sC, and each

inductor is represented by its complex impedance, sL. The circuit equations are then

formulated in the usual way. Using the complex frequency, the mathematical expres-

sions obtained for voltage gain, current gain, input impedance, or output impedance

are ratios of polynomials in s.

We will be concerned in many cases with system transfer functions. These will

be in the form of ratios of, for example, output voltage to input voltage (voltage

transfer function) or output current to input voltage (transconductance function). The

four general transfer functions are listed in Table 7.1.

Once a transfer function is found, we can ﬁnd the result of a steady-state sinu-

soidal excitation by setting

s = jω = j2π f

. The ratio of polynomials in s then

reduces to a complex number for each frequency f. The complex number can be

reduced to a magnitude and a phase.

Table 7.1 Transfer functions of the complex

frequency s

Name of function Expression

Voltage transfer function T(s) = V

(s)/V

(s)

Current transfer function I

(s)/I

(s)

Transresistance function V

(s)/I

(s)

Transconductance function I

(s)/V

(s)

s-Domain Analysis

In general, a transfer function in the s-domain can be expressed in the form

T (s) = K

(s − z

)(s − z

) ···(s − z

)

(s − p

)(s − p

) ···(s − p

)

(7.1)

where K is a constant,

, z

,...,z

are the transfer function “zeros,” and

, p

,...,p

are the transfer function “poles.” When the complex frequency is

7.2.1

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 472 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

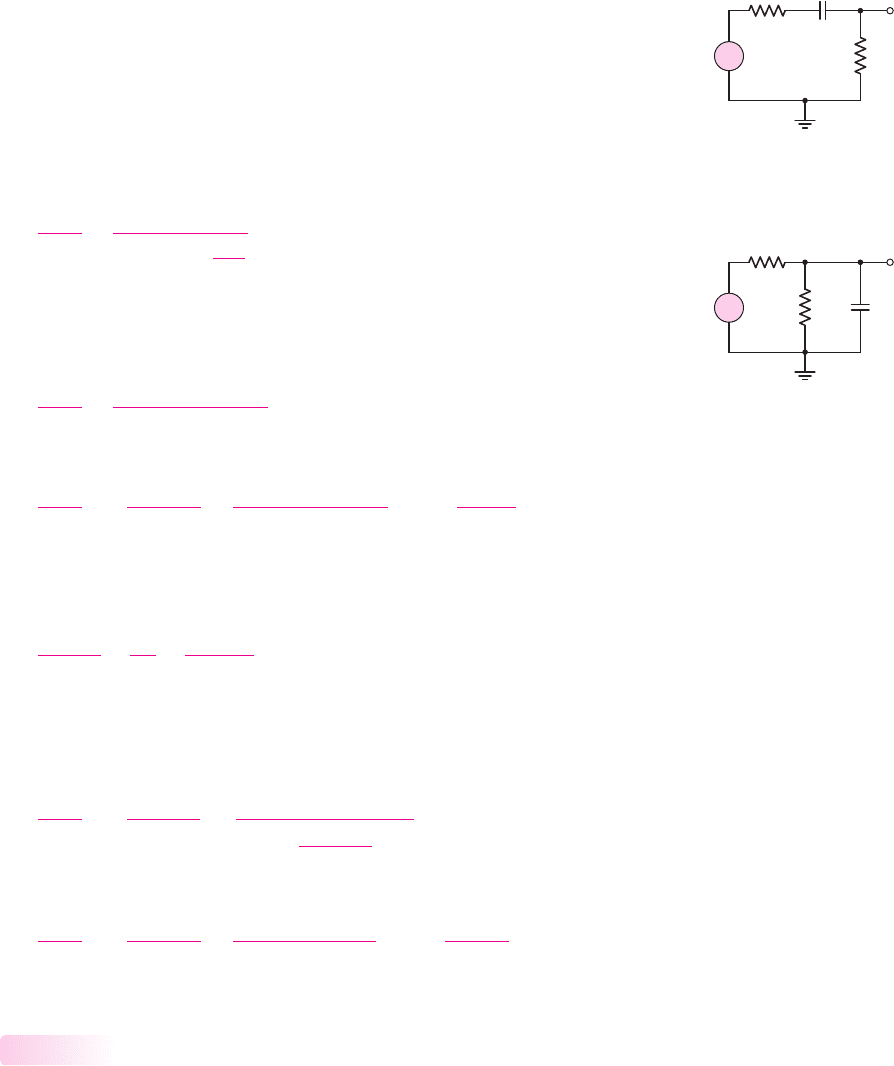
Chapter 7 Frequency Response 473

–

Figure 7.2 Series coupling

capacitor circuit

equal to a zero,

s = z

, the transfer function is zero; when the complex frequency is

equal to a pole,

s = p

, the transfer function diverges and becomes inﬁnite. The

transfer function can be evaluated for physical frequencies by replacing s with

jω

. In

general, the resulting transfer function

T ( jω)

is a complex function, that is, its mag-

nitude and phase are both functions of frequency. These topics are usually discussed

in a basic circuit analysis course.

To introduce the frequency response analysis of transistor circuits, we will

examine the circuits shown in Figures 7.2 and 7.3. The voltage transfer function for

the circuit in Figure 7.2 can be expressed in a voltage divider format, as follows:

(s)

+ R

(7.2)

The elements R

and C

are in series between the input and output signals, and the

element R

is in parallel with the output signal. Equation (7.2) can be written in the

form

(s)

1 + s(R

+ R

(7.3)

which can be rearranged and written as

(s)



+ R



s(R

+ R

1 + s(R

+ R



= K



sτ

1 + sτ



(7.4)

where

is a time constant and is given by

= (R

+ R

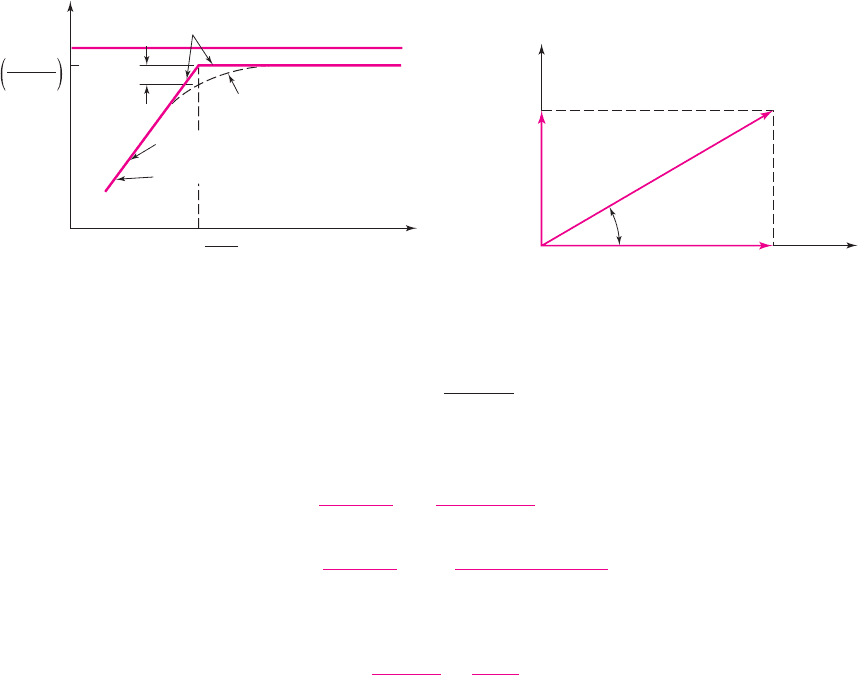
Writing a Kirchhoff current law (KCL) equation at the output node, we can de-

termine the voltage transfer function for the circuit shown in Figure 7.3, as follows:

− V

(1/sC

)

= 0

(7.5)

In this case, the element R

is in series between the input and output signals, and the

elements R

and C

are in parallel with the output signal. Rearranging the terms in

Equation (7.5) produces

(s)



+ R



⎡

⎢

⎣

1 + s



+ R



⎤

⎥

⎦

(7.6)

(s)



+ R



1 + s(R

R



= K



1 + sτ



(7.7)

where

is also a time constant and is given by

= (R

R

First-Order Functions

In our hand analysis of transistor circuits in this chapter, we will, in general, limit

ourselves to the consideration of only one capacitance at a time. We will therefore

be dealing with ﬁrst-order transfer functions that, in most cases, will have the

general form of either Equation (7.4) or (7.7). This simpliﬁed analysis will allow us

to present the frequency responses of speciﬁc capacitances and of the transistors

7.2.2

–

Figure 7.3 Parallel load

capacitor circuit

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 473 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

474 Part 1 Semiconductor Devices and Basic Applications

themselves. We will then compare our hand analysis results with more rigorous so-

lutions, using a computer simulation.

Bode Plots

A simpliﬁed technique for obtaining approximate plots of the magnitude and phase

of a transfer function, given the poles and zeros or the equivalent time constants, was

developed by H. Bode, and the resulting diagrams are called Bode plots.

Qualitative Discussion: Initially, we will consider the magnitude of the voltage

transfer function versus frequency. Before we delve into the mathematics, we can

qualitatively determine the general characteristics of this plot. The capacitor C

Figure 7.2 is in series between the input and output terminals. This capacitor then

behaves as a coupling capacitor.

In the limit of zero frequency (the input signal is a constant dc voltage), the im-

pedance of the capacitor is inﬁnite (an open circuit). In this case, then, the input sig-

nal does not get coupled to the output terminal so the output voltage is zero. In this

case, the magnitude of the voltage transfer function is zero.

In the limit of a very high frequency, the impedance of the capacitor becomes

very small (approaching a short circuit). In this situation, the magnitude of the

output voltage reaches a constant value given by a voltage divider, or

/(R

+ R

)] · V

We therefore expect the magnitude of the transfer function to start at zero for

zero frequency, increase for increasing frequency, and reach a constant value at a rel-

atively high frequency.

Bode Plot for Figure 7.2

Mathematical Derivation: For the transfer function in Equation (7.4), correspond-

ing to the circuit in Figure 7.2, if we replace s by

jω

and deﬁne a time constant

= (R

+ R

, we obtain

T ( jω) =

( jω)



+ R



jωτ

1 + jωτ



(7.8)

The magnitude of Equation (7.8) is

T ( jω)



+ R



⎡

⎣

ωτ



1 + ω

⎤

⎦

(7.9(a))

T ( jf)



+ R





2π f τ



1 + (2π f τ

)



(7.9(b))

We can develop the Bode plot of the gain magnitude versus frequency. We may

note that

|T ( jf)|

= 20 log

|T ( jf)|

. From Equation (7.9(b)), we can write

T ( jf)

= 20 log





+ R



2π f τ



1 + (2π f τ

)



(7.10(a))

7.2.3

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 474 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

Chapter 7 Frequency Response 475

T ( jf)

= 20 log



+ R



+20 log

(2π f τ

)

−20 log



1 + (2π f τ

)

(7.10(b))

We can plot each term of Equation (7.10(b)) and then combine the three plots to form

the ﬁnal Bode plot of the gain magnitude.

Figure 7.4(a) is the plot of the ﬁrst term of equation (7.10(b)), which is just a

constant independent of frequency. We may note that, since

/(R

+ R

)]

is less

than unity, the dB value is less than zero.

Figure 7.4(b) is the plot of the second term of Equation (7.10(b)). When

f = 1/2πτ

, we have 20log

(1) = 0

. The slopes in Bode plot magnitudes are

described in units of either dB/octave or dB/decade. An octave means that frequency

is increased by a factor of two, and a decade implies that the frequency is increased

by a factor of 10. The value of the function 20 log

(2π f τ

)

increases by a factor of

6.02

∼

dB for every factor of 2 increase in frequency, and the value of the function

increases by a factor of 20 dB for every factor of 10 increase in frequency. Hence, we

can consider a slope of 6 dB/octave or 20 dB/decade.

Figure 7.4(c) is the plot of the third term in Equation (7.10(b)). For

f  1/2πτ

, the value of the function is essentially 0 dB and when

f = 1/2πτ

the value is

−3

dB. For

f  1/2πτ

, the function becomes

−20 log

(2π f τ

)

,so

the slope becomes

−6

dB/octave or

−20

dB/decade. A straight-line projection of this

slope passes through 0 dB at

f = 1/2πτ

. We can then approximate the Bode plot

for this term by two straight line asymptotes intersecting at 0 dB and

f = 1/2πτ

This particular frequency is known as a break-point frequency, corner frequency,

−3

dB frequency.

–6 dB/octave

–20 dB/decade

–3 dB

f (log scale)

2pt

f =

(c)

6 dB/octave

20 dB/decade

f (log scale)

2pt

f =

(b)

f (log scale)

(a)

20 log

+ R

Figure 7.4 Plots of (a) the ﬁrst term, (b) the second term, and (c) the third term of

Equation (7.10(b))

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 475 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

476 Part 1 Semiconductor Devices and Basic Applications

20 log

+ R

|T( j

3 dB

Actual curve

Asymptotic

approximation

+6 dB/octave

+20 dB/decade

f (log scale)

2pt

f =

Figure 7.5 Bode plot of the voltage transfer function magnitude

for the circuit in Figure 7.2

The complete Bode plot of Equation (7.10(b)) is shown in Figure 7.5. For

f  1/2πτ

, the second and third terms of Equation (7.10(b)) cancel, and for

f  1/2πτ

, the large negative dB value from Figure 7.4(b) dominates.

The transfer function given by Equation (7.9) is for the circuit shown in Fig-

ure 7.2. The series capacitor C

is a coupling capacitor between the input and output

signals. At a high enough frequency, capacitor C

acts as a short circuit, and the out-

put voltage, from a voltage divider, is

= [R

/(R

+ R

)]V

For very low frequencies, the impedance of C

approaches that of an open circuit,

and the output voltage approaches zero. This circuit is called a high-pass network

since the high-frequency signals are passed through to the output. We can now un-

derstand the form of the Bode plot shown in Figure 7.5.

Imaginary

part

Real part

Figure 7.6 Relation between rectangular and polar

forms of a complex number

The Bode plot of the phase function can be easily developed by recalling the re-

lation between the rectangular and polar form of a complex number. We can write

A + jB = Ke

jθ

, where

K =

√

+ B

and

θ = tan

−1

(B/A)

. This relationship is

shown in Figure 7.6.

For the function given in Equation (7.8), we can write the function in the form

T ( jf) =



+ R





j2π f τ

1 + j2π f τ







+ R



jθ



[|j2π f τ

jθ

]

[|1 + j2π f τ

jθ

]

(7.11(a))

T ( jf) =



jθ





jθ





jθ



j(θ

+θ

−θ

)

(7.11(b))

The net phase of the function

T ( jf)

is then

θ = θ

+θ

−θ

Since the ﬁrst term,

/(R

+ R

)]

, is a positive real quantity, the phase is

= 0

. The second term,

( j2π f τ

)

, is purely imaginary so that the phase is

= 90

◦

. The third term is complex so that its phase is

= tan

−1

(2π f τ

)

. The net

phase of the function is now

θ = 90 − tan

−1

(2π f τ

)

(7.12)

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 476 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07:

Chapter 7 Frequency Response 477

For the limiting case of

f → 0

, we have

tan

−1

(0) = 0

, and for

f →∞

,we

have

tan

−1

(∞) = 90

◦

. At the corner frequency of

f = 1/(2πτ

)

, the phase is

tan

−1

(1) = 45

◦

. The Bode plot of the phase of the function given in Equation (7.11(a))

is given in Figure 7.7. The actual plot as well as an asymptotic approximation is

shown. The phase is especially important in feedback circuits since this can inﬂuence

stability. We will see this effect in Chapter 12.

Bode Plot for Figure 7.3

Qualitative Discussion: Again, we will initially consider the magnitude of the volt-

age function versus frequency. The capacitor C

in Figure 7.3 is in parallel with the

output and then behaves as a load capacitor on the output of a circuit, or may repre-

sent the input capacitance of a follow-on ampliﬁer stage.

In the limit of zero frequency (the input signal is a constant dc voltage), the

impedance of the capacitor is inﬁnite (an open circuit). In this case the output signal

is a constant value given by a voltage divider, or

= [R

/(R

+ R

)] · V

In the limit of a very high frequency, the impedance of the capacitor becomes

very small (approaching a short circuit). In this situation, the output voltage will be

zero, or the magnitude of the voltage transfer function will be zero.

We therefore expect the magnitude of the transfer function to start at a constant

value for zero and low frequencies, and then decrease toward zero at high

frequencies.

Mathematical Derivation: The transfer function given by Equation (7.7) is for the

circuit that was shown in Figure 7.3. If we replace s by

s = jω = j2π f

and deﬁne a

time constant

= (R

R

, then the transfer function is

T ( jf) =



+ R



1 + j2π f τ



(7.13)

The magnitude of Equation (7.13) is

|T ( jf)|=



+ R







1 + (2π f τ

)



(7.14)

A Bode plot of this magnitude expression is shown in Figure 7.8. The low-

frequency asymptote is a horizontal line, and the high-frequency asymptote is a

Phase

45°

90°

1110

Actual curve

Asymptotic

approximation

2pt

f (log scale)

f = f = f =

Figure 7.7 Bode plot of the voltage transfer function

phase for the circuit in Figure 7.2

nea80644_ch07_469-558.qxd 06/13/2009 08:07 PM Page 477 F506 Hard disk:Desktop Folder:Rakesh:MHDQ134-07: