Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.

Замечание. Универсальная подстановка
2
x
tgt =
во многих случаях приводит к
сложным вычислениям, так как при ее применении sinx и cosx выражаются через t
в виде рациональных дробей t
2
.
В некоторых частных случаях нахождение интегралов вида
()
∫
dxxcos,xsinR
может
быть упрощено.
1. Если
- нечетная функция относительно sinx, т.е.
, то интеграл рационализируется подстановкой cosx=t.
(
xcos,xsinR
(
cos,xsinR−=
)
)
)
)
)
)
()
xxcos,xsinR −
2. Если
- нечетная функция относительно cosx, т.е.
, то интеграл рационализируется с помощью
подстановки sinx=t.
(
xcos,xsinR
(
cos,xsinR−=
()
xxcos,xsinR −
3. Если - четная функция относительно sinx и cosx, т.е. если
,то следует применить подстановку tgx=t.
(
xcos,xsinR
()
xsinRxcos =
(
xcos,,xsinR −−
Примеры.
1.
()
(
)
∫∫
−
+
=
+
dx
xsinxcos
xsinxsin
dx
x2cos
xsinxsin
22
33
Так как подынтегральная функция нечетна относительно sinx, то полагаем cosx=t.
Отсюда
sin . dxsindt ,1t21xcos2x2cos ,t1x
2222
−=−=−=−=
Таким образом,
(
)
(
)
(
)
(
)
()
()
∫∫∫
∫∫∫∫
+
+
−
−=
−
−=
−
−=
=
−
−
=
−
−
=
−
−−
=
+
c
12t
12t
ln
24
3
2
t
1t2
2td
22
3
2
t
1t2
dt
2
3
dt
2
1
dt
1t2
4t2
2
1
1t2
dt2t
1t2
dtt2
dx
x2cos
xsinxsin
2
2
2
2
2
2
2
23
.
Следовательно,
∫
+
+
−
−=
+
c
1xcos2
1xcos2
ln
8
23
xcos
2
1
dx
x2cos
xsinxsin
3
.
2.
∫
+
+
dx
xsinxsin
xcosxcos
42
53
.
Здесь подынтегральная функция является нечетной относительно косинуса.
Поэтому применяем подстановку sinx=t, тогда
. dtxdxcos ,t1xsin1xcos
222
=−=−=
Следовательно,
()
(
)
(
)( )
∫∫∫
+
−−
=
+
+
=
+
+
dt
t
t
t2t1
dx
xsinxsin
xcosxcos1xcos
dx
xsinxsin
xcosxcos
42
22
42
22
42
53
Выделяя целую часть подынтегральной дроби и разлагая остаток на простейшие
дроби, получим
()
(
)
()
2222
22
t1
6
t
2
1
t1t
t2t1
+
−+=
+
−−
.
Поэтому
()
(
)
()
()
∫
+−−=+−−=
+
−−
.cxsinarctg6
xsin
2
xsincarctgt6
t
2
tdt
t1t
t2t1
22
22
Заметим, что в этом случае интеграл всегда может быть записан в виде
(
)
∫
xdxcosxcos,xsin*R
2
.
3.
∫
−⋅+
.
xcosxcosxsin2xsin
dx
22
Здесь подынтегральная функция является четной относительно sinx и cosx,
поэтому полагаем t=tgx.
Тогда
22
t1
t
xtg1
tgx
xsin ,arctgtx
+
=
+
==
22
2
t1
1
xtg1
1
xcos ,
t1
dt
dx
+
=
+
=
+
=
()
()
()
∫∫
∫∫
+
++
−+
=+
++
−+
=
−+
+
=
−+
=
=
+
−
+
⋅
+
+
+
+
=
−⋅+
c
21tgx
21tgx
ln
22
1
c
21t
21t
ln
22
1
21t
1td
1t2t
dt
t1
1
t1
1
t1
t2
t1
t
t1
dt
xcosxcosxsin2xsin
dx
2
2
2
2
22
2
2
2
22
Замечание. То же преобразование можно сделать проще, если в исходном
интеграле числитель и знаменатель разделить на cos
2
x.
∫∫∫
−+
=
−+
=
−⋅+ 1tgx2xtg
dtgx
1tgx2xtg
xcos
dx
xcosxcosxsin2xsin
dx
22
2
22
.
6.9.2. Интегралы вида
∫
⋅ .xdxcosxsin
nm
1-й случай. По крайней мере один из показателей m или n нечетное целое,
положительное число.
Если n- нечетно, то применяется подстановка sinx=t, если же m- нечетно, то
подстановка cosx=t.
Примеры.
1.
dxxcosxsin
54
∫
⋅
Положим sinx=t, cosxdx=dt, тогда
()
(
)
.cxsin
9
1
xsin
7
2
xsin
5
1
ct
9
1
t
7
2
t
5
1
dttdtt2dtt
dtt1txdxcosxsin1xsinxdxcosxsin
975975864
2
24
2
2454
++−=++−=+−=
=−=−=⋅
∫∫∫
∫∫∫
2.
()
∫∫∫
=−=⋅=
−−
xdxsinxcosxcos1xdxcosxsin
xcosxcos
xdxsin
3
4
2
3
4
3
3
3
Положив cosx=t, -sinxdx=dt, получим:
()
.cxcoscos
5
3
xcos
3
ct
5
3
t3dttdttdttt1
32
3
3
5
3
1
3
2
3
4
3
4
2
+⋅+=
=++=+−=−−=
−−−
∫∫∫
2-ой случай. Показатели степеней m и n - четные положительные числа. Здесь
нужно преобразовать подынтегральную функцию с помощью формул.

)x2cos1(
2
1
xcos
)x2cos1(
2
1
xsin
x2sin
2
1
xcosxsin
2
2
+=
−=
=⋅
Пример.
.
∫
⋅ xdxcosxsin
22
Здесь
=
=⋅=⋅
2
222
x2sin
2
1
)xcosx(sinxcosxsin
).x4cos1(
8
1
2
x4cos1
4
1
x2sin
4
1
2
−=
−
==
Отсюда
.Cx4sin
32
1
x
8
1
xdx4cos
8
1
dx
8
1
dx)x4cos1(
8
1
xdxcosxsin
22
+−=
=−=−=⋅
∫∫∫∫
6.9.3. Интегралы вида
)xdxctg èëè( xdxtg
mm
∫
∫
, где m – целое положительное число
При нахождении таких интегралов применяется формула
)1
xsin
1
xctg( 1
xcos
1
xtg
2
2
2
2
−=−=
,
с помощью которой последовательно снижается степень тангенса и котангенса.
Пример.
.Cxcosln
2
xtg
4
xtg
6
xtg
dx1
xcos
1
tgx
4
xtg
6
xtg
dx1
xcos
1
xtg
6
xtg
xdxtg)tgx(xdtgdx1
xcos
1
xtgxdxtg
246
2
46
2
3
6
55
2
57
+++−=
=
−+−=
−−=
=−=
−=
∫∫
∫∫∫∫
6.9.4. Интегралы вида
∫
∫
∫
⋅⋅⋅ .nxdxsinmxsin ,nxdxcosmxcos ,nxdxcosmxsin
Используя формулы
[]
[]
[]
,)cos()cos(
2
1
sinsin
)cos()cos(
2
1
coscos
)sin()sin(
2
1
cossin
βαβαβα
βαβαβα
βαβαβα
+−−=⋅
−++=⋅
−++=⋅
представляем подынтегральную функцию в виде суммы косинусов или синусов.
Пример.
[]
.Cx3cos
6
1
x7cos
14
1
xdx3sin
2
1
xdx7sin
2
1
dx)x3sin(x7sin
2
1
xdx5cosx2sin
++−=−=
=−+=⋅
∫∫
∫∫
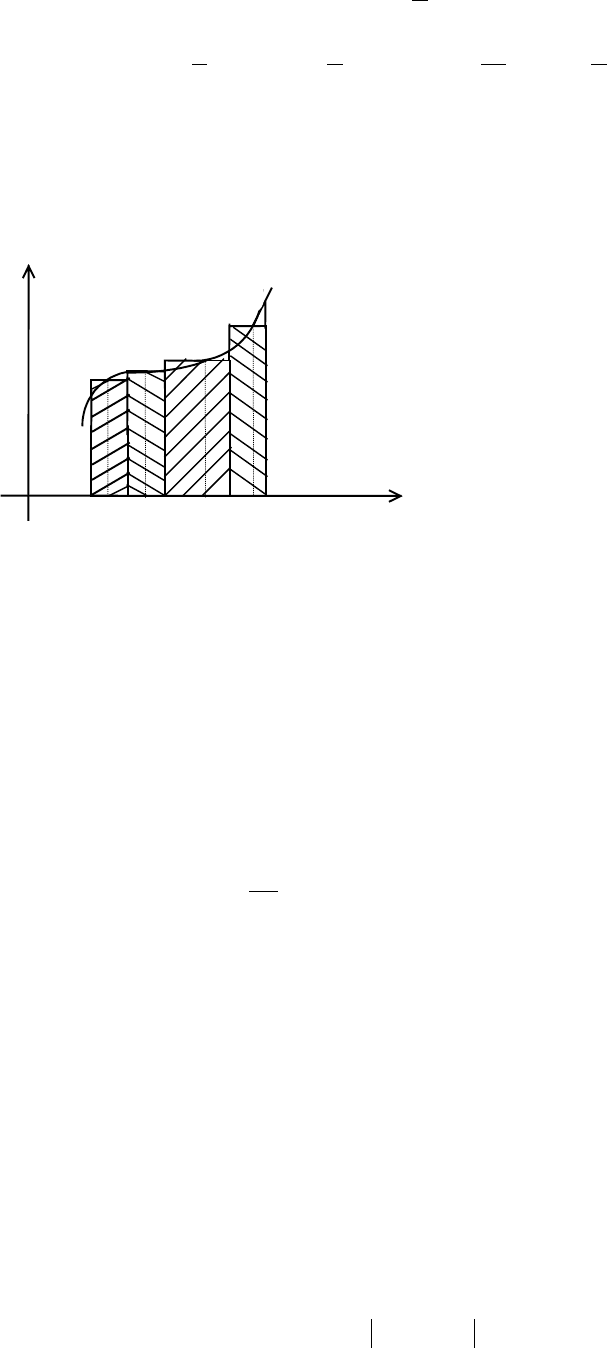
7. Определенный интеграл и его геометрические приложения
7.1. Интегрируемость функции на сегменте
y
f(
ξ
1
) f(
ξ
2
) f(
ξ
3
) f(
ξ
n
)
a b
x
0
ξ
1
x
1
ξ
2
x
2
ξ
3
x
3
ξ
n
x
n
x
Рис.1
Пусть функция f(x) задана на сегменте
[a,b] (a<b). Обозначим че-
рез Т разбиение [a,b] при помощи не
совпадающих друг с другом то-
чек a=x
0
<x
1
<...<x
n
=b на n частич-
ных сегментов [x
0
,x
1
]...[x
n-1
, x
n
]. Точки
x
0
,x
1
,...,x
n
называются точ-
ками разбиения Т. Пусть
i
ξ
-
произвольная точка частичного
сегмента [x
i-1
,x
i
]. Разность ∆x
i
=x
i
-x
i-1
будем называть длиной частич-
ного сегмента [x
i-1
,x
i
].
Определение 1. Число
{
ii
,xI
}
ξ
, где
{}
∑
=
∆=∆++∆+∆=
n
1i
iinn2211ii
x)(fx)(f...x)(fx)(f,xI
ξξξξξ
называется интегральной суммой функции f(x), соответствующей данному
разбиению Т сегмента [a,b] и данному выбору промежуточных точек
ξ
i
на
частичных сегментах [x
i-1
,x
i
].
Обозначим
)n,1i(xmax
i
i
=∆=∆ - диаметр разбиения Т сегмента [a,b].
Геометрический смысл интегральной суммы
{}
ii
,xI
ξ
. Рассмотрим
криволинейную трапецию - фигуру, ограниченную графиком функции f(x) (будем
считать ее положительной и непрерывной), двумя ординатами, проведенными в
точках a и b оси абсцисс и осью абсцисс.
Интегральная сумма
{
ii
,xI
}
ξ
- площадь ступенчатой фигуры (рис.1)
Определение 2. Число I называется пределом интегральных сумм
{
ii
,xI
}
ξ
при
∆→0, если для ∀ε>0 можно указать такое положительное число ))((
ε
δ
δ
, что для
любого разбиения Т сегмента [a,b], максимальная длина
∆ частичных сегментов
которого <
δ, независимо от выбора точек
i
ξ
на сегментах [x ,x ] выполнено
неравенство
i-1 i
{
}
εξ
<− I,xI
ii
Если интегральная сумма
при ∆→0 имеет пределом число I, то будем
записывать это так
.
{
}
ii
,xI
ξ
{}
ii
0
,xlimI
ξ
→∆
=
Определение 3. Функция f(x) называется интегрируемой по Риману на [a,b], если
существует конечный предел I интегральных сумм этой функции при
∆→0.
Указанный предел I называется определенным интегралом функции f(x) по [a,b] и
обозначается так:
∫
=
b
a
dx)x(fI
Из рисунка видно, что определенный интеграл численно равен площади
криволинейной трапеции, определяемой графиком функции f(x) на [a,b].
Справедлива следующая теорема. Неограниченная на [a,b] функция f(x) не
интегрируема на этом сегменте.
Доказательство: Пусть функция f(x) неограничена на [a,b], тогда она
неограничена на некотором частичном сегменте [x
k-1
,x
k
] любого данного
разбиения Т сегмента [a,b]. Тогда слагаемое f(
k
ξ
)∆x
k
интегральной суммы
{
}
ii
,xI
ξ
,
отвечающее этому разбиению Т за счет выбора т.
k
ξ
может быть сделано как
угодно большим по абсолютной величине, т.е. интегральные суммы
{
}
ii
,xI
ξ
отвечающие любому разбиению Т, не ограничены и поэтому не существует
конечного предела интегральных сумм. Итак, будем рассматривать лишь
ограниченные на [a,b] функции.
Замечание: Отметим, что вообще говоря, не всякая ограниченная на [a,b]
функция является интегрируемой на этом сегменте.
Проверить это положение для функции Дирихле (значения в рациональных
точках 1, а в иррациональных - 0). Эта функция не интегрируема на [a,b].
7.2. Верхние и нижние суммы и их свойства
Пусть функция f(x) - ограниченная на [a,b] функция, т.е. (
∃m,M)
(
∀x∈[a,b]):[m ≤ f(x) ≤ M]. Т - разбиение [a,b] точками a=x
0
<x
1
<...<x
n
=b.
Обозначим через M
i
- точную верхнюю и через m
i
- точную нижнюю грани этой
функции на [x
i-1
,x
i
].
Суммы
∑
=
∆=∆++∆+∆=
n
1i
iinn2211
xMxM...xMxMS
s
∑
=
∆=∆++∆+∆=
n
1i
iinn2211
xmxm...xmxm
называются верхней и нижней суммами функции f(x) для данного разбиения Т
сегмента [a,b].
Заметим, что любая интегральная сумма
{
}
ii
,xI
ξ
данного разбиения Т
сегмента [a,b] заключена между верхней и нижней суммами S и s этого разбиения.
Геометрический смысл верхней и нижней сумм. Рассмотрим для простоты
положительную и непрерывную функцию f(x) и криволинейную трапецию,
определяемую этой функцией.
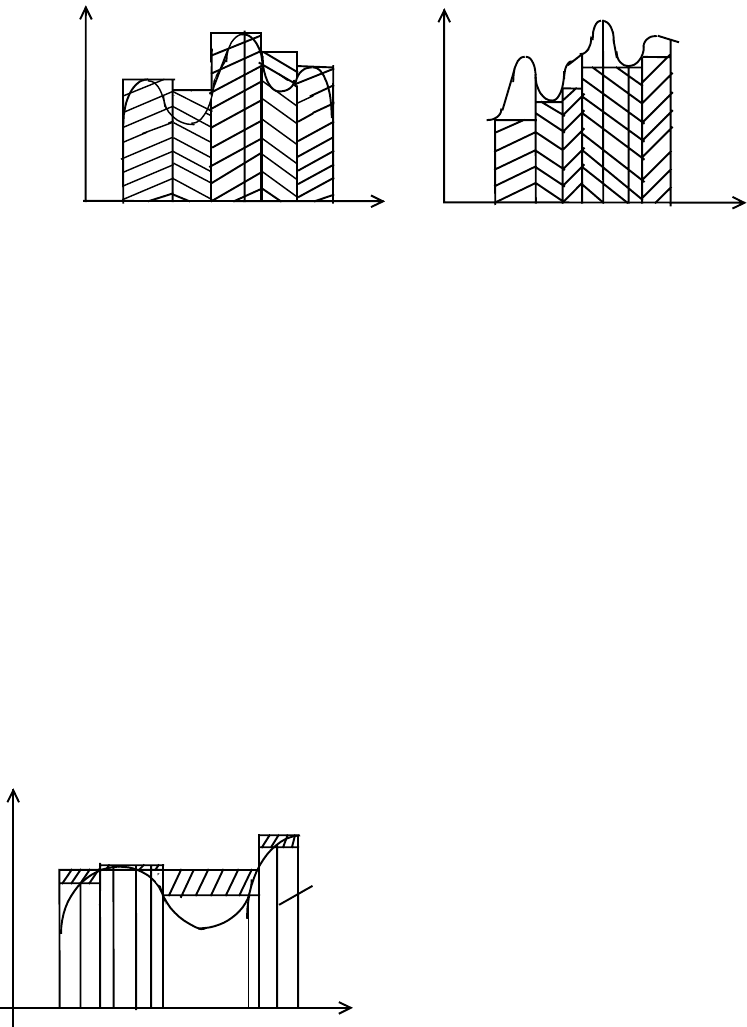
y y
f(x) f(x)
M
i
M
i
m
i
m
i
a=x
0
x
i-1
x
i
b=x
n
x a=x
0
x
i-1
x
i
b=x
n
x
Рис.1 Рис.2
M
i
и m
i
в случае непрерывности функции представляют собой
максимальное и минимальное значения этой функции на частичном сегменте [x
i-
1
,x
i
] разбиения Т, S и s - площади заштрихованных ступенчатых фигур,
изображенных на рисунках 1 и 2 соответственно.
Свойства верхних и нижних сумм подробно изложены в [8] (стр. 319-321),
поэтому приведем лишь формулировки теорем и прокомментируем каждую из
них с помощью рисунков.
Свойство 1. Для любого фиксированного разбиения Т и для любого
ε>0
промежуточные точки
i
ξ
на сегментах [x
i-1
,x
i
] можно выбрать так, что
интегральная сумма
{}
ii
,xI
ξ
будет удовлетворять неравенствам
0
≤S-
{
ii
,xI
}
ξ
<ε. Точки
i
ξ
можно выбрать и таким образом, что интегральная сумма
будет удовлетворять неравенствам
{
}
ε
ξ
<
−
≤
s,xI
ii
0 .
y
f(
ξ
n
)
f(
ξ
1
) M
1
M
2
f(
ξ
2
) f(x) M
i
M
n
f(
ξ
i
)
a=x
0
ξ
1
x
1
ξ
2
x
2
ξ
i
x
i
ξ
n
b=x
n
x
Рис. 3
На рисунке 3 изображена функция
f(x), заданная на сегменте [a,b].
i
ξ
-
промежуточные точки на частичных
сегментах [x
i-1
,x
i
]
Преобразуем разность
S
{}
ii
,xI
ξ
− =
M
1
∆x
1
+ M
2
∆x
2
+... M
i
∆x
i
+...+ M
n
∆x
n
--
f(
1
ξ
)∆x
1
- f(
2
ξ
)∆x
2
-...-
-f(
i
ξ
)∆x
i
-...- f(
n
ξ
)∆x
n
=
= [M
1
-f(
1
ξ
)]∆x
1
+[M
2
-f(
2
ξ
)]∆x
2
+...+
+[M
i
- f(
i
ξ
)]∆x
i
+...+[M
n
- f(
n
ξ
)]∆x
n
.
Здесь S - верхняя сумма. Каждое слагаемое последней суммы представляет
собой площадь заштрихованного прямоугольника, поэтому
{
ii
,xIS
}
ξ
− есть сумма площадей заштрихованных прямоугольников, которая,
очевидно, может быть сколь угодно уменьшена за счет выбора точек
i
ξ
(если
промежуточные точки
i
ξ
выбирать близкими к точкам сегментов [x
i-1
,x
i
], в
которых функция f(x) принимает значения M
i
).
Для нижних сумм рассуждения проводятся аналогичным образом.
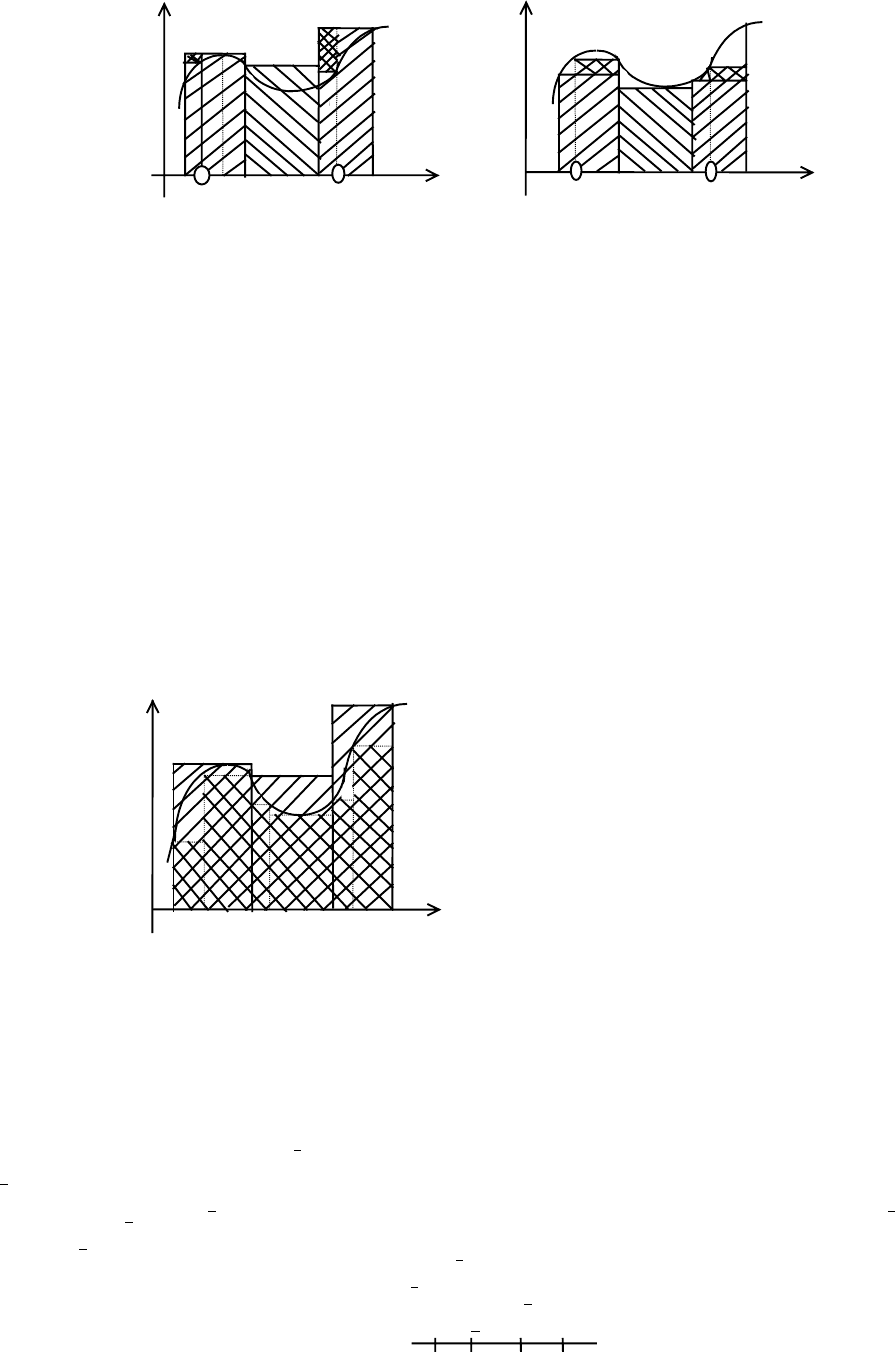
Свойство 2. Если разбиение T'сегмента [a,b] получено путем добавления новых
точек к точкам разбиения Т этого сегмента, то верхняя сумма S' разбиения T' не
больше (S'
≤S) верхней суммы S разбиения Т, а нижняя сумма s' разбиения T' не
меньше (s
≤s') нижней суммы s разбиения Т.
y y
L M Q
B C E
A D K N
a=x
0
t
1
x
1
x
2
t
2
x
3
=b x a=x
0
t
1
x
1
x
2
t
2
x
3
=b x
Рис. 4 Рис. 5
На рис. 4 точки x
0
, x
1
, x
2
, x
3
- точки разбиения сегмента [a,b],
соответствующие разбиению Т. Кружками отмечены новые точки t
1
, t
2
, которые
вместе с точками x
i
дают новое разбиение T' сегмента [a,b].
Сегменты [x
0
,x
1
] и [x
2
,x
3
] поделились на сегменты [x
0
,t
1
], [t
1
,x
1
] и [x
2
,t
2
],
[t
2
,x
3
], соответственно. Верхняя сумма на сегментах [x
0
,t
1
] и [x
2
,t
2
] уменьшилась на
величину, равную площадям прямоугольников ABCD и KLMN, а на остальных
частичных сегментах осталась без изменения, поэтому верхняя сумма S'
разбиения T' уменьшилась по сравнению с верхней суммой.
На рис.5 приведена аналогичная картина для нижних сумм.
Свойство 3. Пусть T' и T'' любые два разбиения [a,b]. Тогда нижняя сумма одного
из этих разбиений не превосходит верхнюю сумму другого. Именно, если s', S'; s'',
S'' соответственно нижние и верхние суммы разбиений T' и T'', то s'
≤S''; s''<S'.
y
x
x
0
=
ξ
0
=a
ξ
1
x
1
ξ
2
x
2
ξ
3
x
3
=
ξ
4
=b
Рис.6
На рис. 6 одинарной
штриховкой показана верхняя
сумма S' разбиения T'
сегмента [a,b] точками
x
0
=a<x
1
<x
2
<x
3
=b, а двойной
штриховкой - нижняя сумма
s'' разбиения T'' сегмента [a,b]
точками
ξ
0
=a<ξ
1
<ξ
2
<ξ
3
<ξ
4
=b
Свойство 4. Множество {S} верхних сумм данной функции f(x) для
всевозможных разбиений сегмента [a,b] ограничено снизу. Множество {s}
нижних сумм ограничено сверху.
Обозначим через
I точную нижнюю грань множества {S} верхних сумм
{}
SinfI = , а через I точную верхнюю грань множества {s} нижних сумм
{
}
ssupI
=
.
Числа
I и I называются соответственно нижним и верхним интегралами Дарбу от
функции f(x). Легко показать, что
I ≤ I
s
I
I
S
Свойство 5. Пусть разбиение T' [a,b] получено из разбиения Т добавлением к
последнему р новых точек, и пусть s',S'; s, S - соответственно нижние и верхние
суммы разбиений T' и Т. Тогда для разностей S-S' и s'-s может быть получена

оценка, зависящая от максимальной длины ∆ частичных сегментов разбиения Т,
числа р добавленных точек и точных верхней и нижней граней М и m функции
f(x) на сегменте [a,b], а именно: S-S'
≤(M-m)⋅р⋅∆ и s'-s ≤(M-m)⋅р⋅∆
y
S-
′
S
=сумме площадей В С
прямоугольников
M-m
M
A D
m
x
0
ξ
1
x
1
x
2
ξ
2
x
3
∆
x
4
=b x
Рис.7
На рис.7 точки x
0
= a < x
1
< x
2
< x
3
< x
4
= b соответствуют разбиению Т
сегмента [a,b], а две добавленные точки
ξ
1
и ξ
2
образуют вместе с точками x
i
:
x
0
=a<ξ
1
<x
1
<x
2
<ξ
2
<x
3
<x
4
=b разбиение T' этого сегмента.
Одинарной штриховкой показана верхняя сумма S разбиения Т, а двойной
штриховкой два прямоугольника, сумма площадей которых дает уменьшение S до
величины S'. Если через М и m обозначить точные верхнюю и нижнюю грани
функции f(x) на [a,b], а через
∆ максимальную длину частичного сегмента [x
i-1
,x
i
]
разбиения Т, то площадь прямоугольника ABCD, равная (M-m)
∆x будет больше
площади каждого из двух прямоугольников, заштрихованных двойной
штриховкой, отсюда очевидна оценка: S-S'≤(M-m)∆⋅2 (здесь 2 - число
добавленных точек). Для нижних сумм может быть дана аналогичная
интерпретация.
В заключение данной темы приведем без доказательства формулировку
теоремы, известной под названием леммы Дарбу, имеющей фундаментальное
значение для построения теории в теме “Определенный интеграл”.
Лемма Дарбу. Верхний и нижний интегралы Дарбу
I и I от функции f(x)
по сегменту [a,b] являются соответственно пределами верхних и нижних сумм
при
∆→0, т.е. IS
0
=
→∆
lim и Islim
0
=
→∆
.
Замечание 1. Число
I
)
, например, называется пределом верхних сумм S при ∆→0,
если
()(
(
)
[
]
εδδε
<−⇒<∆∀>∃>∀ IST:00 .
Замечание 2. В случае, когда
I =I = I лемма Дарбу позволяет переходить к
пределам в неравенствах вида
{
}
S,Is
i
x
i
≤
≤
ξ
при стремлении к нулю диаметра ∆
разбиения Т сегмента [a,b]. При этом s
→I и S→I, откуда
{
}
I,xI
ii
→
ξ
.
7.3. Необходимое и достаточное условие интегрируемости функции на
сегменте
Вышеперечисленные свойства верхних и нижних сумм позволяют доказать
теорему об интегрируемости функции на сегменте.
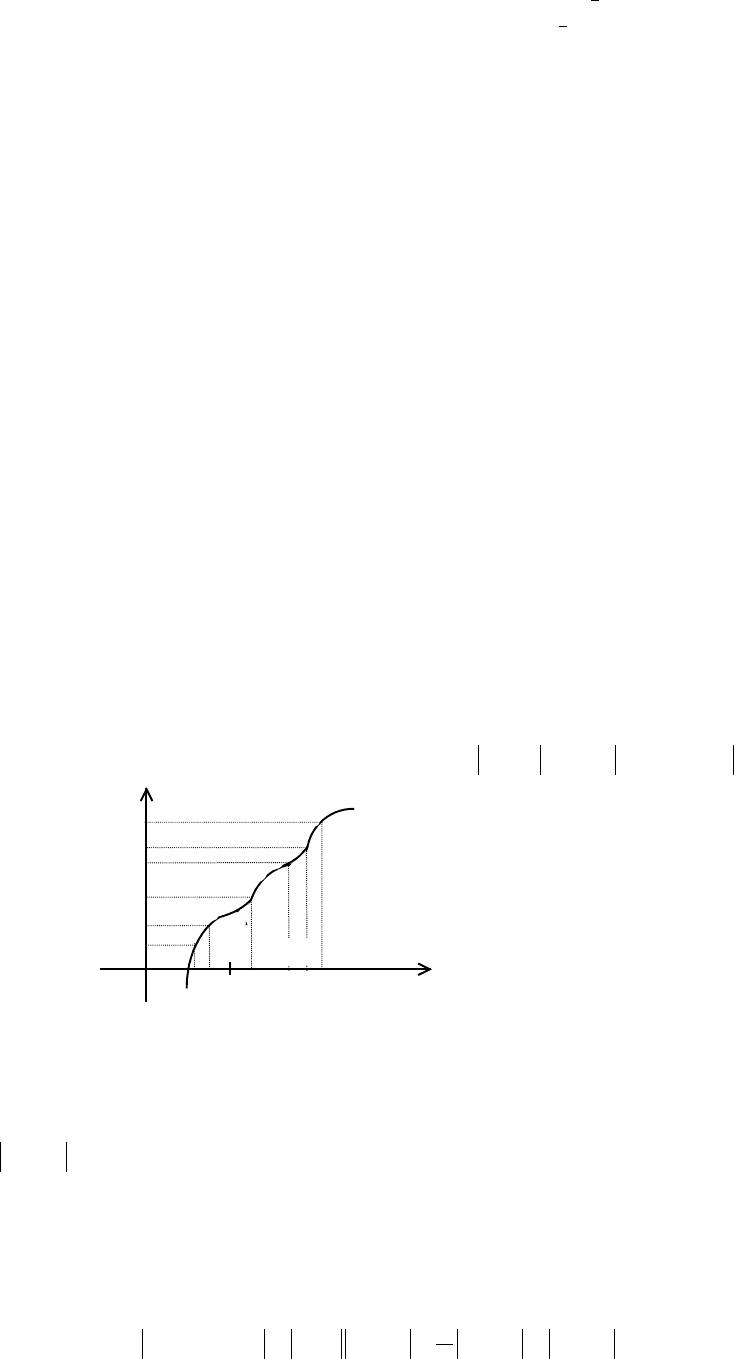
Теорема. Для того, чтобы ограниченная на сегменте [a,b] функция f(x) была
интегрируемой на этом сегменте, необходимо и достаточно, чтобы
0>∀
ε
нашлось
такое разбиение Т сегмента [a,b], для которого
S - s
≤ ε.
Не будем приводить доказательство этой теоремы, отметим лишь, что из
неравенства S - s
≤ ε следует равенство I =I = I, что в силу замечания 2
гарантирует существование предела интегральных сумм
{
}
ii
,xI
ξ
, равного I.
Определение. Число
ω
i
= M
i
- m
i
, где M
i
и m
i
- точные верхняя и нижняя грани
функции f(x) на [x
i-1
,x
i
] называются колебанием функции f(x) на сегменте [x
i-1
,x
i
].
Очевидно, что
ω
i
> 0, ибо M
i
≥ m
i
.
После введенного определения колебания функции f(x) разность
0xx)mM(xmxMsS
n
1i
ii
n
1i
iii
n
1i
ii
n
1i
ii
≥∆=∆−=∆−∆=−
∑∑∑∑
====
ω
(так как все
ω
i
≥0 и ∆х
i
>0) и последнюю теорему можно сформулировать так:
Для того, чтобы ограниченная на сегменте [a,b] функция f(x) была интегрируема
на [a,b], необходимо и достаточно, чтобы для
0>
∀
ε
нашлось такое разбиение Т
сегмента, для которого
εω
≤∆
∑
=
n
1i
ii
x
[] []
{}()()
≤∆∃>∀⇔∈∧∈
∑
=
εωε
n
1i
ii
x:T0b,aL)x(fb,aB)x(f .
7.4. Равномерная непрерывность функции на множестве
Пусть функция f(x)
∈ (непрерывна на множестве {x}; {x} - множество
замкнуто или нет, конечно или бесконечно), т.е. она непрерывна в каждой точке
этого промежутка х
{}
xc
0
∈{x}. Это означает, что
()()
{
}()
[
]
εδδε
<−⇒<−∈∀>∃>∀ )x(f)x(fxx:xx00
00
y
ε
ε
ε
ε
x
0
-
δ
x
0
x
0
+
δ
x
1
δ
2
f(x
0
)
f(x
1
)
δ
1
Отметим, что для фиксированного
ε число δ зависит не только от ε, но и
от точки х
0
.
Существует ли при заданном
ε
такое
δ, которое годилось бы для
всех точек х
0
из этого промежутка?
Определение. Функция f(x) называется равномерно непрерывной на {x}, если для
0>∀
ε
можно указать такое положительное число δ(δ=δ(ε)) зависящее только от
ε, что для любых двух точек x' и x'' множества {x}, удовлетворяющих условию
δ
<
′
−
′′
xx , выполняется неравенство
ε
<
−
|)'x(f)''x(f|
Пример 1. y=lnx равномерно непрерывна на полупрямой x
≥ 1. В самом деле, по
теореме Лагранжа для любых
1x,1x ≥
′
′
≥
′
(пусть для определенности x'<x'').
xxxx
1
xx)(f)x(f)x(f
′
−
′′
<
′
−
′′
=
′
−
′′′
=
′
−
′′
ξ
ξ
, ибо x'<ξ<x'' и ξ>1
Следовательно, по данному ε>0, если выбрать 0<δ≤ ε, то из
εδ
<
′
−
′′
⇒<
′
−
′′
)x(f)x(fxx
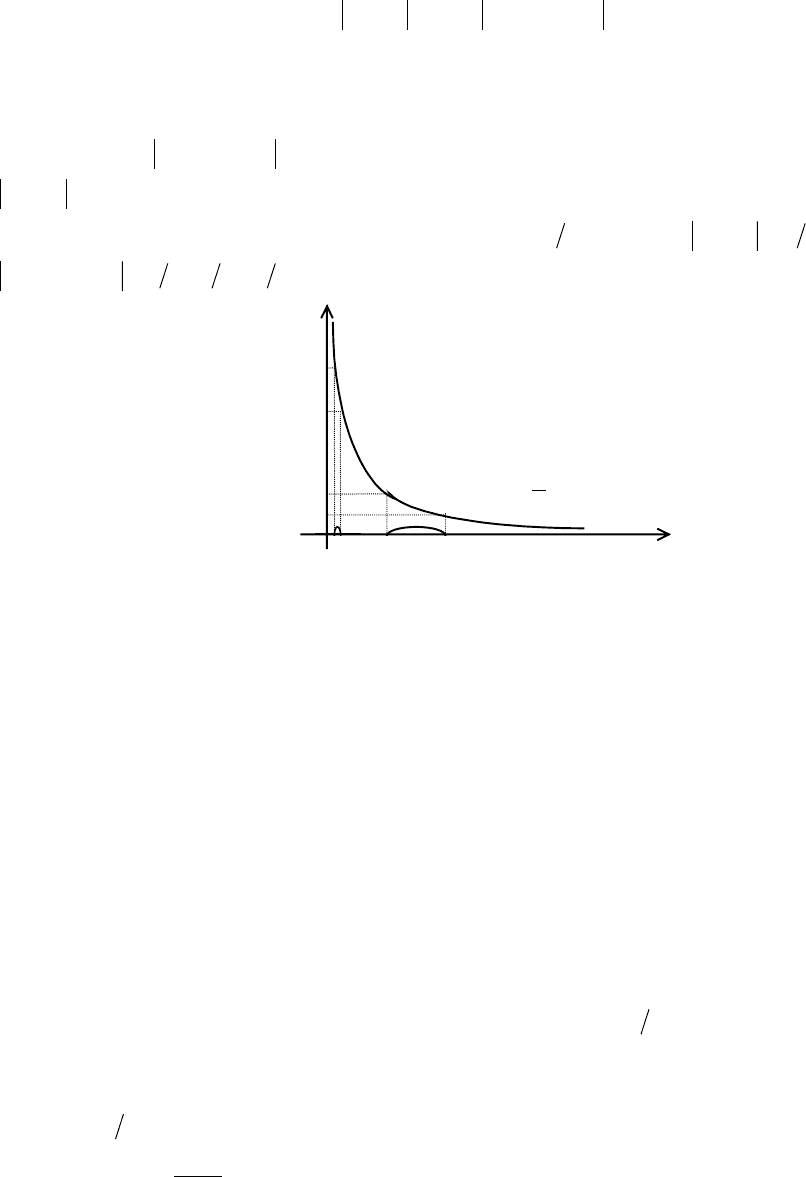
Пример 2. Функция f(x)=1/x на интервале (0,1) непрерывна, но не является на нем
равномерно непрерывной, т.е. для некоторого ε>0 нельзя выбрать δ>0 такое, что
неравенство
ε
<
′
−
′′
)x(f)x(f будет выполнено для всех x'' и x' при условии, что
δ
<
′
−
′′
xx .
Покажем это. Пусть δ>0, x'= δ, x''= 2
δ
, тогда 2xx
δ
<
′
−
′′
, а величина
δδδ
112)x(f)x(f =−=
′
−
′′
может быть сделана сколь угодно большой.
y
y
2
ε
y
1
ε
δ
2
δ
1
x
y
x
=
1
δ
2
→
0 при y
2
→∞
Для непрерывной на сегменте функции справедлива следующая теорема.
Теорема (Кантора). Непрерывная на сегменте [a,b] функция f(x) равномерно
непрерывна на этом сегменте.
Теперь, с очевидностью, вытекает следствие: пусть функция f(x)
непрерывна на [a,b], тогда для
(
)
(
)
00 >
∃
>
∀
δ
ε
такое, что на каждом,
принадлежащем сегменту [a,b] частичном сегменте [c,d], длина d-c которого
меньше
δ, колебание ω функции f(x) меньше ε. Сформулируем и докажем
следующую основную теорему.
Теорема. Непрерывная на сегменте [a,b] функция f(x) интегрируема на этом
сегменте.
Пусть дано
(
0>∀
)
ε
. Так как f(x) равномерно непрерывна на сегменте [a,b]
(теорема Кантора), то для положительного числа
)ab(
−
ε
можно указать такое
δ>0, что при разбиении Т сегмента [a,b] на частичные сегменты [x
i-1
,x
i
], длина
максимального из которых
∆<δ, колебание ω
i
функции f(x) на каждом из них
меньше
)ab( −
ε
(следствие из теоремы Кантора). Тогда для таких разбиений Т
ε
ε
ω
−
<∆=−
∑
=
n
1i
ii
b
xsS =∆
∑
=
n
1i
i
x
a
и выполняется достаточное условие интегрируемости
функции f(x).
Замечание. Если f(x) имеет на [a,b] конечное число точек разрыва 1-го рода, то
функция f(x) также интегрируема на этом сегменте. При этом, если, например,
f(x) разрывна в одной точке x=c, то
, и значение этих
интегралов не зависит от значения функции в точке с.
∫∫∫
+=
b
c
c
a
b
a
dx)x(fdx)x(fdx)x(f
7.5. Основные свойства определенного интеграла
