Пинчук С.И. Организация эксперимента при моделировании и оптимизации технических систем

Подождите немного. Документ загружается.

121

корреляции r

. Проверку выполняют сравнением расчётного зна-

чения

с табличным при выбранном уровне значимости α. Коэф-

фициент корреляции

признаётся статистически значимым, если

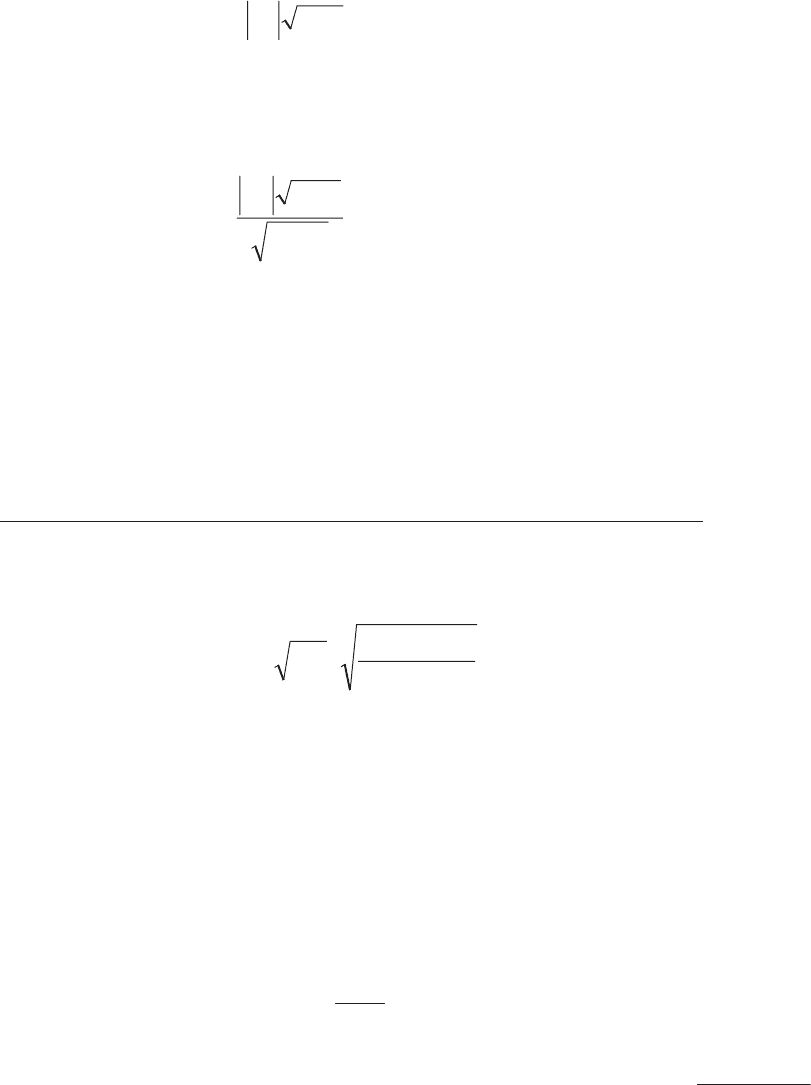
выполняется соотношение:

≥ r

табл. α, n–1

1–nr

. (6.19)

Значимость коэффициента парной корреляции

может быть

оценена также с помощью t-критерия Стьюдента: r

признаётся

значимым, если выполняется соотношение:

≥ t

r–1

2–nr

табл. α, n–2

. (6.20)

Если выборка имеет большой объём и хорошо представляет ге-

неральную совокупность (репрезентативна), то заключение о тес-

ноте линейной корреляционной связи между переменными

Х и Y,

полученное по данным выборки, в известной степени может быть

распространено и на генеральную совокупность.

6.4 Оценка точности определения значений зависимой

переменной по уравнению регрессии

Определим стандартную ошибку оценки значений ŷ

по линей-

ному уравнению регрессии:

–∑(y

=S=S

yxyx

. (6.21)

Стандартная ошибка S

всегда выражается в тех же единицах,

что и зависимая переменная Y.

Выборочная ошибка оценки ŷ

имеет тенденцию преуменьшать

величину стандартной ошибки в генеральной совокупности. Реко-

мендуется вносить в неё поправку.

Величина стандартной ошибки оценки для генеральной сово-

купности σ

и её квадрата σ

могут быть определены по величине

стандартной выборочной ошибки оценки S

и её квадрата по фор-

мулам:

2–n

=σ

; (6.22)

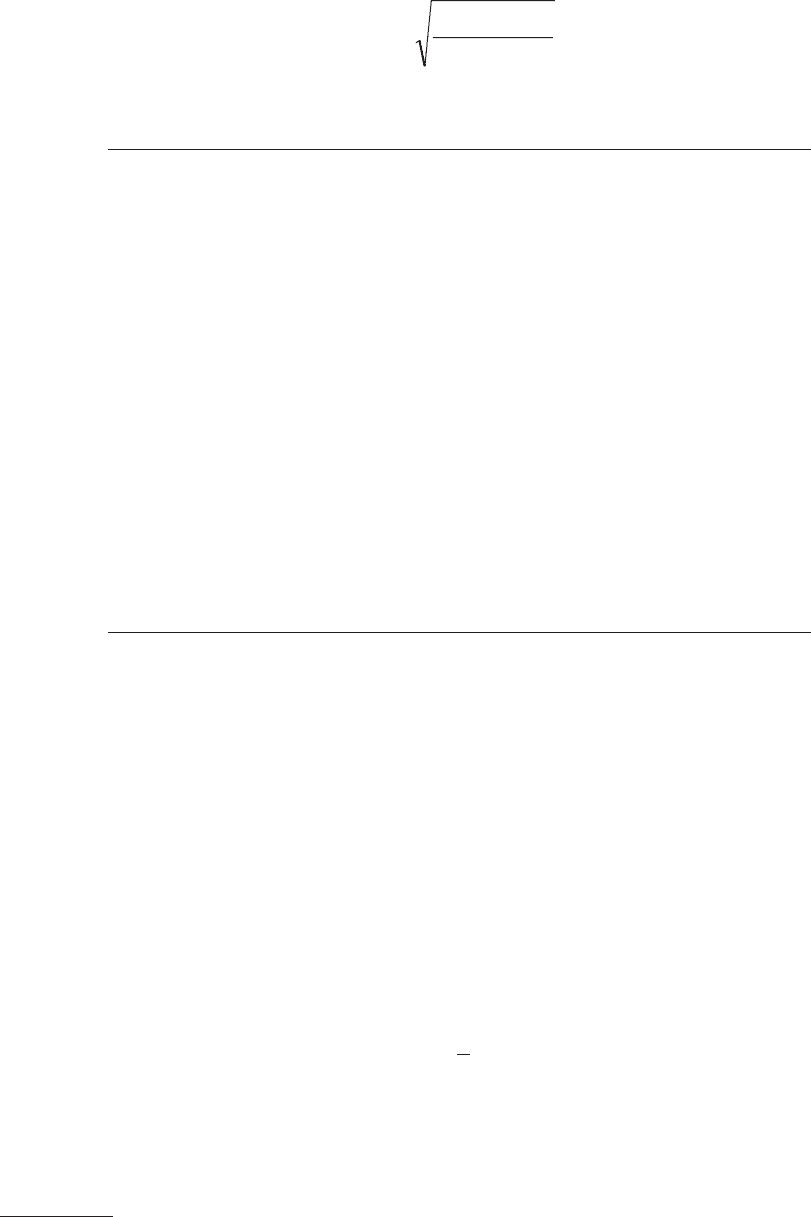
122

2–n

–(y

=σ

∑

. (6.23)

6.5 Коэффициент детерминации

Во многих случаях возникает вопрос о том, какую часть наблю-

даемой вариации зависимой переменной

Y можно объяснить вли-

янием независимой переменной Х. Для этого служит коэффициент

детерминации.

Выборочный коэффициент детерминации при линейной зависи-

мости переменных обозначается d

и может быть определён из со-

отношения:

xyx

= rd

. (6.24)

Он измеряет долю тех элементов вариации в

Y, которые содер-

жатся также в Х, т.е. долю в общей вариации переменной Y той её

части, которая определена влиянием Х. Коэффициент детермина-

ции часто выражают в %.

6.6 проверка адекватности уравнения регрессии

и ошибки предсказаний

Для проверки адекватности полученного уравнения регрессии

экспериментальным данным применяют дисперсионный анализ

(введён английским математиком-статистиком Р.А. Фишером).

Метод дисперсионного анализа заключается в расчленении об-

щей суммы квадратов отклонений зависимой переменной от её

средней величины на несколько компонентов.

Оценка адекватности уравнения регрессии производится с помо-

щью критерия Фишера, который определяется как отношение дис-

персии, обусловленной регрессией, т.е. дисперсии адекватности:

∑

)1/(k +)y

–(y=S

ад.

(6.25)

к остаточной дисперсии:

∑

)1–k–/(n)y–y

(=S

ост.

: (6.26)

123

∑

)1–k–/(n)y–y

(

)1/(k +)y

–(y

ост.

ад.

расч.

, (6.27)

где

(k + 1) = f

– число степеней свободы дисперсии адекватности;

(n – k – 1) = f

– число степеней свободы остаточной дисперсии;

k – число значимых коэффициентов регрессии.

В случае парной линейной регрессии

= 2; f

= n – 2.

Расчётное значение критерия Фишера

расч.

сравнивают с таблич-

ным при выбранном уровне значимости

α.

Если выполняется соотношение

расч.

≤ F

табл. α, f1, f2

, (6.28)

то регрессионная модель признаётся адекватной и может быть ис-

пользована для предсказания значений зависимой переменной

при всех значениях независимой переменной Х в пределах наблю-

давшихся при эксперименте значений последней.

Определяют стандартную ошибку аппроксимации, т.е. разности

(ŷ

– y), которую можно использовать для оценки ошибки предсказа-

ний зависимой переменной Y по регрессионной линейной модели:

2–n

)y–y

(

апр.

∑

. (6.29)

Рассчитывают также среднюю относительную ошибку аппрокси-

мации (в % от средней величины зависимой переменной

Y) по фор-

муле:

,%10 0

/ny

)

2–/(n

)

y–

(

ε =

апр.

∑

. (6.30)

Чем меньше величина

ε, тем более точными будут предсказания

значений переменной Y по уравнению регрессии.

6.7 три показателя корреляции и регрессии,

их значение и применение

Коэффициент регрессии b

указывает среднее число единиц,

на которое увеличивается или уменьшается величина параметра Y

при каждом увеличении фактора Х на единицу его измерения.

124

Коэффициент детерминации

измеряет ту долю изменений в

величинах измеряемого параметра Y, которая может быть объясне-

на влиянием фактора

Х и оценивается в связи с этим влиянием.

Стандартная ошибка оценки S

указывает, насколько близко оце-

ненные по регрессионной модели величины ŷ совпадают с наблюда-

емыми при эксперименте величинами оцениваемого параметра Y.

Эти три коэффициента измеряют различные аспекты отношений

взаимосвязи параметров Х и Y.

Какой из этих показателей должен привлечь наибольшее внима-

ние зависит от того, чему придаётся на данном этапе исследования

наибольшее значение: абсолютной величине изменений Y – т.е. рег-

рессии, близости соразмерных изменений Х и Y – т.е. корреляции

или точности оценки значений переменной Y, характеризуемой ве-

личиной стандартной ошибки.

Но все эти показатели имеют своё место при анализе изучаемой

корреляционной зависимости Y от X и ни один не должен быть со-

вершенно опущен или забракован.

6.8 множественный корреляционно-регрессионный

анализ

Те же математические принципы, на которых основано опреде-

ление параметров уравнения с одной независимой переменной,

могут быть распространены и на решение задач о влиянии любого

числа факторов на выходной параметр объекта исследования.

Линейное уравнение регрессии для k переменных имеет вид:

ŷ = b

+ ∑b

, i = 1, 2 … k

то есть,

ŷ = b

+ b

+ ..... + b

. (6.31)

Для определения параметров уравнения составляют систему

уравнений, которая в общем случае

k переменных и n строк эмпи-

рических данных принимает вид:

+ b

∑x

+ b

∑x

+ ..... + b

∑x

+ ..... + b

∑

= ∑y

∑x

+ b

∑

+ b

∑x

+ ..... +b

∑x

+ ..... +b

∑x

= ∑x

∑x

+ b

∑x

+ b

∑

+ ..... + b

∑x

+ ..... + b

∑x

= ∑x

125

∑x

+ b

∑x

+ b

∑x

+ ..... + b

∑

+ ..... + b

∑x

= ∑x

∑x

+ b

∑x

+ b

∑x

+ ..... +b

∑x

+ ..... +b

∑

= ∑x

Решение таких задач при k ≥ 3 и многочисленной выборке вы-

полняется с помощью ЭВМ.

Самым простым случаем множественной линейной корреляци-

онной связи является связь трёх переменных, из которых одна за-

висимая (функция

Y) и две независимые (факторы или аргументы

и Х

Рассматривая Y как функцию двух аргументов Х

и Х

, следует

учитывать, что Х

и Х

также могут быть корреляционно связаны

между собой. В таком случае

Y = F(X

, X

) может рассматриваться

как результат сочетания трёх парных зависимостей, описываемых

коэффициентами парной корреляции

, r

). Изменение Х

вызывает изменение

Y. Кроме того, изменение X

вызывает изме-

нение X

и, наоборот, изменение X

вызывает изменение Х

, эти из-

менения, в свою очередь, приводят к дополнительному изменению Y.

Таким образом, воздействие каждого фактора на изучаемый пара-

метр Y может быть в действительности больше или меньше того,

которое учитывается линейным уравнением регрессии.

Степень изменения

Y под воздействием изменений X

и X

для

случая линейной корреляционной зависимости оценивается коэф-

фициентом множественной корреляции R.

R показывает тесноту связи между Y и несколькими факторами,

всегда положителен и изменяется от 0 до 1. Для вычисления R ис-

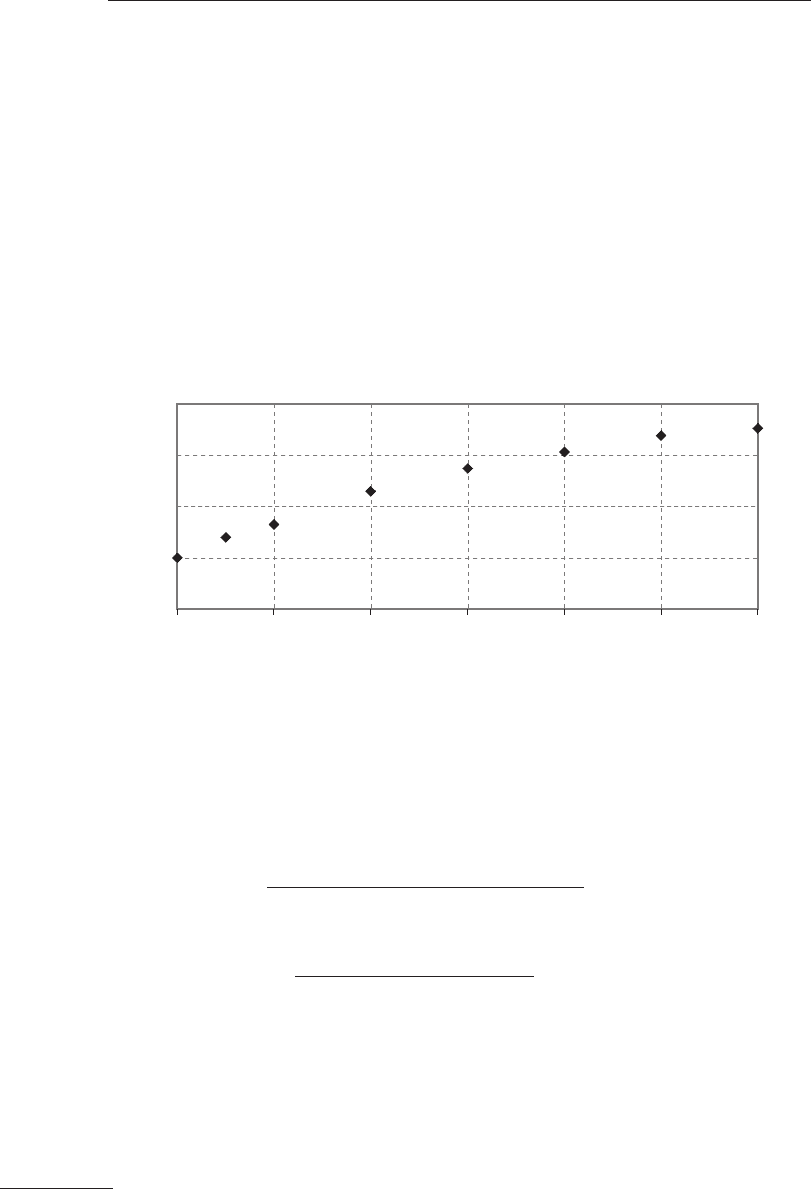
пользуют формулы:

])(R–1[

1–к–п

1–п

–1R =

, (6.32)

∑

)y–(y

–(y

–1=R

, (6.33)

где

∑(y

– ŷ

)

− сумма квадратов отклонений относительно регрессии;

∑(y

– y)

− сумма квадратов отклонений относительно среднего.

Квадрат коэффициента множественной корреляции называется

множественным коэффициентом детерминации. Он характеризует

ту долю изменений зависимой переменной

Y, которая обусловле-

на влиянием всех факторов, входящих в регрессионную модель.

126

Значимость множественного коэффициента корреляции R и его квад-

рата – коэффициента детерминации

проверяется по F-критерию.

Расчётное значение

F для множественного коэффициента корре-

ляции R

y/x

, ... , x

определяется по формуле:

)1–k–)/(nR–1(

)2–/(k

, ..., xy/x

..., xy/x

расч.

. (6.34)

Множественный коэффициент корреляции считается значимым,

если выполняется соотношение:

расч.

≥ F

табл.α, f

, f

где f

= k – 2, f

= n – k – 1.

При большом числе факторов

, X

… X

из-за сложного пе-

реплетения различных взаимосвязей определяют частные коэффици-

енты корреляции, оценивающие тесноту взаимосвязи двух факторов

при исключении влияния остальных факторов на каждый из них.

Частные коэффициенты корреляции могут быть любого порядка,

в зависимости от числа факторов, влияние которых на действие ос-

тальных факторов исключено. Так, при исключении влияния одного

фактора получают частный коэффициент корреляции первого по-

рядка. При исключении влияния двух факторов получают частный

коэффициент корреляции второго порядка и т.д.

Понятно, что парные коэффициенты корреляций факторов могут

рассматриваться как частные коэффициенты корреляции нулевого

порядка.

Ниже приведены формулы для вычисления частных коэффици-

ентов корреляции первого и второго порядка:

)r–1)(r–1(

r–r–r

=)(r

231312

312

; (6.35)

])(r–1][)(r–1[

)(r)(r–)(r

=)(r

423

413

423413412

3412

. (6.36)

В круглых скобках указаны парные коэффициенты между соот-

ветствующими факторами при исключении влияния на них факто-

ров, которые поддерживаются на постоянном уровне и указаны за

круглыми скобками.

127

Получив уравнение регрессии, необходимо оценить его возмож-

ности. В большинстве случаев достаточно оценить значимость ко-

эффициентов регрессии и адекватность полученного уравнения

регрессии экспериментальным данным.

Проверка значимости коэффициентов регрессии в случае множес-

твенной регрессии аналогична парной. Если имеет место соотноше-

ния

расч.b

≤ t

табл.α,n – 2

, то соответствующий коэффициент регрессии b

признаётся незначимым, что свидетельствует о несущественном вли-

янии соответствующего фактора на параметр Y. В принципе этот фак-

тор

может быть исключен из уравнения регрессии.

Однако значение t

расч.b

зависит не только от самого коэффици-

ента регрессии b

, но и от того, насколько сильно факторы корре-

лированны между собой. Поэтому при исключении какого-либо из

факторов из уравнения регрессии значимость других коэффициен-

тов регрессии может измениться. Отсев несущественно влияющих

факторов при их взаимной коррелированной взаимосвязи сложен

и удовлетворительного решения пока не имеет.

Остальной статистический анализ уравнений множественной

регрессии аналогичен анализу уравнений парной регрессии.

6.9 нелинейная парная регрессия и криволинейная

корреляция

В тех случаях, когда по правилам, изложенным в предыдущих па-

раграфах, гипотеза линейной корреляционной связи двух перемен-

ных может быть отброшена или когда при графическом изображе-

нии явно просматривается нелинейность изучаемой зависимости

Y = F(X), прибегают к процедурам статистической оценки коэффи-

циентов нелинейного уравнения регрессии Y на X по эксперимен-

тальным данным, а корреляцию называют криволинейной.

Теория криволинейной корреляции решает те же за дачи, что и

теория линейной корреляции, а именно – установление формы и

тесноты корреляционной связи.

Для оценки тесноты криво линейной корреляции служит выбороч-

ное корреляционное отношение η

, которое далее будем обозначать

через η и для простоты речи называть корре ляционным отношением.

Связь тем сильнее, чем больше η.

Корреляционное отношение удовлетворяет двойному неравенству:

0 ≤ η ≤ 1. (6.37)

128

Если η = 0, то переменная Y с переменной X корреля ционной

зависимостью не связана.

Если η = 1, то переменная Y связана с переменной X функ-

циональной зависимостью.

Выборочное корреляционное отношение не меньше абсолютной

величины выборочного коэффициента корре ляции:

η ≥ |r

|. (6.38)

Если выборочное корреляционное отношение равно абсолют-

ной величине выборочного коэффициента корреля ции, то имеет

место линейная корреляционная за висимость.

При криволинейной зависимости

Y от Х для оценки той доли ва-

риации зависимой переменной Y, которая определяется влиянием

независимой переменной Х, следует употреблять индекс детерми-

нации d, величина которого может быть выражена так:

d = η

; (6.39)

d = η

· 100, %. (6.40)

Корреляционное отношение

η служит мерой тесноты корреля-

ционной связи любой формы, в том числе и линейной. В этом со-

стоит преимущество корреляционного отношения перед коэффи-

циентом корреляции, который оценивает тесноту лишь линейной

корреляционной зави симости. Вместе с тем, корреляционное от-

ношение обладает недостатком: оно не позволяет судить, насколь-

ко близко расположены точки, найденные по данным наблюдений,

к кривой определенного вида, например, к параболе, гиперболе и

т.д. Это объясняется тем, что при определении корреляционного

отношения форма связи во внимание не принимается.

Для выбора формы нелинейной регрессии Y на X также может

быть использован метод наименьших квадратов, но для этого при-

бегают к линеаризующим преобразованиям, так как только линей-

ные по параметрам функции могут быть количественно описаны

методом наименьших квадратов.

В таблице 6.1 приведены часто встречающиеся парные зависи-

мости и линеаризующие преобразования переменных. Выполнив

соответствующие преобразования x

→ x

ʹ и y

→ y

ʹ , по методу на-

именьших квадратов определяют значение коэффициентов b

и b

уравнения парной регрессии:

yʹ = b

+ b

. (6.41)

129

Затем выполняют обратные преобразования, т.е. по b

и b

опре-

деляют b

и b

в соответствии с указаниями в таблице 6.1.

Рекомендуется проверить различные известные формы парной

взаимосвязи, чтобы выбрать наилучшую, с точки зрения точности

предсказания значений функции отклика Y.

Критерием оптимальности выбора формы функциональной пар-

ной нелинейной зависимости переменной Y = F(X) может служить

наибольшая величина из статистич ески значимых коэффициентов пар-

ной корреляции r

yʹxʹ

либо наименьшая остаточная дисперсия S

ост.

Таблица 6.1

Функции и линеаризующие преобразования

№

п/п

Функция

Линеаризующие преобразования

Преобразован-

ные

переменные

Выражения

для величин

и b

по значениям

yʹ xʹ

1. y = b

+ b

/x y x b

2. y = 1/(b

+ b

x) 1/y x b

3. y = x/(b

+ b

x) x/y x b

4. y = b

ℓgy x ℓgb

ℓgb

5. y = b

ℓny x ℓnb

6. y = 1/(b

+ b

–x

) 1/y e

-x

7. y = b

ℓgy ℓgx ℓgb

8. y = b

+ b

ℓgx y ℓgx b

9. y = b

/(b

+ x) 1/y x b

1/b

10. y = b

x/(b

+ x) 1/y 1/x b

1/b

11. y = b

ℓny 1/x ℓnb

12. y = b

+ b

y x

130

6.10 пример синтеза линейной регрессионной модели

Рассмотрим пример синтеза линейной регрессионной модели

по данным экспериментального исследования зависимости плот-

ности прессовок из порошка меди γ от давления прессования P.

В таблице 6.2 приведены математические ожидания плотности прес-

совок при различных давлениях прессования – от 100 до 700 МПа.

Графическое изображение экспериментальных данных, приведен-

ное на рисунке 6.1, позволяет предположить наличие линейной

корреляционной зависимости γ (г/см

) от Р(МПа).

Исходные данные для вычисления коэффициентов уравнения

регрессии и вспомогательные расчеты приведены в табл. 6.2 и гра-

фически изображены на рисунке 6.1.

100

200 300 400 500 600

Р, МПа

γ,

г/см

рис 6.1. Исходные данные зависимости плотности прессовок γ

от давления прессования

Выполняем расчет коэффициентов уравнения регрессии по фор-

мулам (6.8) и (6.9).

8131,4=

2950–1422500·8

20248·2950–05,51·1422500

;

004253,0=

2950–1422500·8

05,51·2950–20248·8

Для проверки гипотезы о статистической значимости коэффици-

ентов уравнения регрессии осуществляем расчет значений крите-