Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.

10.10 Green’s Theorem for Analytical Continuation 319
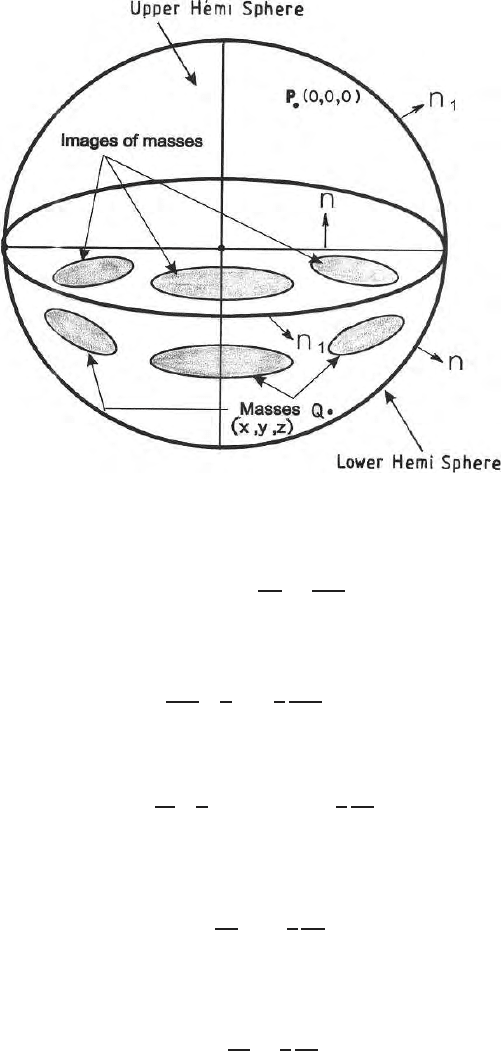
Fig. 10.5. Distribution of masses in the lower half space and their images in the
upper half space
φ = φ
1
and
∂φ
∂n
=
∂φ
1
∂n
1
on the plane. For upper hemisphere
φ
1
∂
∂n
1
1
r
−
1
r
∂φ
1
∂n
1
ds = 0 (10.49)
with no masses inside. Thus
Plane
φ
∂
rn
1
r
ds = −
Plane
1
r
∂φ
∂n
ds. (10.50)
Therefore (10.49) can be rewritten as
φ
P
= −
1
2π
Plane
1
r
∂φ
∂n
ds. (10.51)
Taking z axis as positive vertically downward and normal to the p lane we get
φ
P
= −
1
2π
s
1
r
∂φ
∂n
ds (10.52)

320 10 Green’s Theorem in Potential Theory
This is the upward continuation integral. This integral is valid for the upper
hemisphere where (10.52) is valid. The plane of o bservation at any height in
the upper hemisphere does not contain any mass responsible fo r the potential
φ. Further details on the topic is discussed in Chap. 16.
10.11 Green’s Theorem for Two Dimensional Problems
For a two-dimensional problem, the potential is logarithmic
φ = −2G
m
ℓ
ℓn
C
r
(10.53)
This is the expression for gravitational potential due to a long line source of
mass m
ℓ
. C is any arbitrary constant. For two-dimensional problems
(a) the Laplace and other connecting equations are
(i)
∂
2
φ
∂x
2
+
∂
2
φ
∂y
2
= 0 (10.54)
(ii)
∇
2
ℓn
1
r
=0. (10.55)
(b) Gauss’s divergence theorem is
div
F= Lim
∆s→0
F.
−→
dl
∆S
(10.56)
where a s for three dimensional problem it is
div
F= Lim
∆ν→0
s
F.ds
∆ ν
. (10.57)
(c) Green’s second identity can be obtained from
F=φ grad ψ
where both φ and ψ are functions of x and y. It is given by
s
φ∇
2
ψ −ψ∇
2
φ
ds =
ℓ
φ
∂ψ
∂n
− ψ
∂φ
∂n
dℓ. (10.58)
(d) The mean value theorem is the value of the logarithmic potential at the
centre of the circle and it is the average of potentials at the circumference.
(e) For Green’s formula in two dimensions φ = ℓn
1
r
and ψ is any function.
Here
r=
(x −ξ)
2
+(y− η)
2
.
10.12 Three to Two Dimensional Conv ersion 321
If the point P is outside (Fig. 10.4) the closed surface, ℓn
1
r
is continuous
and harmonic. When the point P is inside, we shall have to draw a small
circle surrounding the point P to avoid singulari ty as it is done in the 3-D
case. Green’s formula for the 2 -D case is given by
ψ
p
=
1
2π
ℓ
ℓn
1
r
∂ψ
∂n
− ψ
∂
∂n
ℓn
1
r
dℓ
=2π
ℓ
ψ
∂
∂n
ℓnr− ℓnr
∂ψ
∂n
dℓ. (10.59)
When the point P is outside, we get
0=
1
2π
ℓ
ψ
∂
∂n
ℓnr− ℓnr
∂ψ
∂n
dℓ. (10.60)
When the point P is on the boundary of an area in two dimensions
ψ
p
=
1
π
ℓ
ψ
∂
∂n
ℓnr− ℓnr
∂ψ
∂n
dℓ. (10.61)
If the point P lies on the boundary C, the point P is excluded from the region
of integration by enclosing it in a small circle of radius ‘a’ and the ‘a’ is made
to approach zero. The factor
1
2π
enters here instead of
1
4π
,since2π is the
circumference of an unit circle. Every potential possesses continuous partial
derivatives.
10.12 Three to Two Dimensional Conversion
For three to two dimensional conversions of the potential problems the fol-
lowing factors are to b e changed i.e.
3-D2-D
(i) Volume → area
(ii) Surface → curve lines
(iii) Sphere → circle
(iv)
1
r
→ ℓn
1
r
(v) 4π → 2π
(vi) 2π → π
(vii)
∂
2
φ
∂z
2
+
∂
2
φ
∂y
2
+
∂
2
φ
∂z
2
or
∂
2
φ
∂x
2
+
∂
2
φ
∂z
2
(10.62)
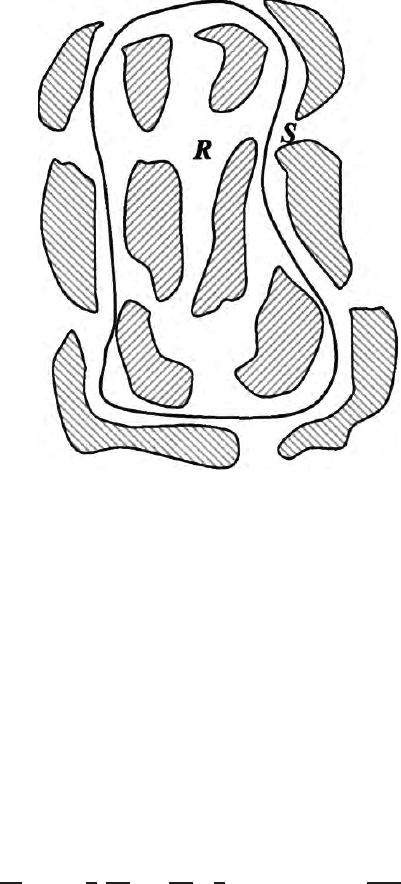
322 10 Green’s Theorem in Potential Theory
Fig. 10.6. Distribution of masses both inside and outside the region R and surface S
10.13 Green’s Equivalent Layers
Fo r Poisson’s field when the source is included
∇
2
φ = −4πρ (10.63)
where ρ is the volume density of mass and ∇
2
φ = 0 for Laplace field in a
source free region. Let us assume a certain region R has the volume V and
is bounded by the surface S. Some masses are present inside and some are
outside the domain boundaries as shown in the Fig. 10.6. Potential at a point
P due to the distribution of mass using Green’s theorem is
φ
p
=
1
4π
s
1
r
.
∂φ
∂n
− φ
∂
∂n
1
r
ds +
v
ρdv
r
dν (10.64)
I
1
↓ I
2
↓
I
2
indicates the components of potential at a point P due to all the sources
included in the volume V. The surface S is drawn to separate the volume V
that contains all the sources inside and the sources outside the region.

10.13 Green’s Equivalent Layers 323
I
1
=
s
1
r
1
4π
.
∂φ
∂n
ds −
s
φ
4π
.
∂
∂n
1
r
ds (10.65)
σ
s
↓↓
Surface distribution of masses Double layer distribution
The first integral represents the potentials due to simple surface distribu-
tion σ
s
. The second integral represents the potential due to surface distribution
of double layer dipoles of charge or mass distribution of moment m. Hence we
can show the redistribution of masses as shown in the Fig. 10.7. We can divide
the total normal ind u ction equally in upper and lower hemisphere and each
sector will have −2πGM where M is the total anomalous mass. This induc-
tion is independent of the total number of bodies present and their s izes and
shapes. Therefore, on the surface, we can write the expression for the integral
on gravity anomaly as
surface
∆gds =4πGM (10.66)
where ∆g is the gravity anomaly and M is the mass excess due to density
contrast with the host rock. Surface integration is carried over the plane of
observation.
ρdν
r
+
σ
s
ds
r
+
↓↓
Volume distribution Surface distribution
of masses of masses
Fig. 10.7. Mass distribution in the region both inside and outside the region can
be changed to mass distribution inside,surface distribution of masses and dipolar
distribution
324 10 Green’s Theorem in Potential Theory
m
4π
∂
∂n
1
r
ds
↓
Double layer
distribution of masses
The sources outside the surface can be redistributed and taken on the bound-
ing surface S as a simple surface distribution and a double layer distribution.
In a source free region where ∇
2
φ =0,thepotentialis
φ
p
=
1
4π
s
1
r
∂φ
∂n
− φ
∂
∂n
1
r
ds (10.67)
This is known as the Green’s third formula. From this equation, we can see
that the value of a harmonic function in the interior region of volume V, where
it is regular, is determined. We know the value of the function and its normal
derivatives on the bound ary, We assumed also that φ and
∂φ
∂n
are continuous
on approaching the boundary S.
Green’s third formula states that: every regular harmonic function can be
represented as the sum of the potentials due to a surface distribution and a
double layer distribution on the surface.
Green’s theorem of equivalent layer states that
(a) the effect of matter lying outside of any closed surface S may be replaced
at all the interior points by the superposition of a single layer and a double
layer on S.
(b) The effect of matter lying within a closed surface may be replaced at all
the exterior points by the superposition of a single layer and a double
layer.
(c) The matter contained outside (or inside) any closed equipotential sur-
face S in a given field can be spread over the surface with a sur face
density -
1
4π
∂ψ
∂n
at a point on the surface without altering the potential
at any p oint in the field inside (or outside) S. Some parts of the matter
are also distributed in the form of double layer with dipole moment
m
4π
.
distribution and is knows as Green’s equivalent layers and it explain s the
ambiguity in the potential fields i.e., many different sets of distribution
of masses can generate the same type of gravity responses on the surface.
Ambiguity do exist in other s calar and vector potential fields also.
10.14 Unique Surface Distribution
In a region bounded by S (Fig. 10.8), if φ
0
is harmonic outside and φ
i
is
harmonic inside, then one can write from Green’s theorem
φ
i
=
1
4π
1
r
∂φ
i
∂n
0
− φ
i
∂
∂n
i
1
r
ds (10.68)
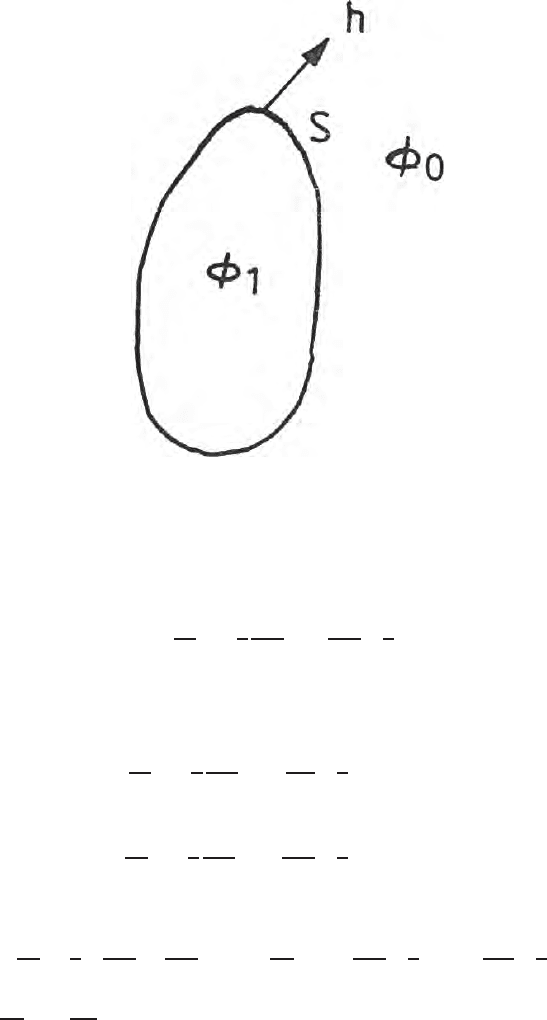
10.14 Unique Surface Distribution 325
Fig. 10.8. Unique surface distribution when the potential is harmonic both inside
and outside
when the observation point is also o u t side, one gets
0=
1
4π
1
r
∂φ
i
∂n
0
− φ
i
∂
∂n
0
1
r
ds (10.69)
The two formulae are for potential inside and outside when the observation
point is inside. When the observation p oint is outside, One gets
0=
1
4π
1
r
∂φ
0
∂n
− φ
0
∂
∂n
i
1
r
ds → inside (10.70)
and
φ
0
=
1
4π
1
r
∂φ
0
∂n
− φ
0
∂
∂n
0
1
r
ds → outside (10.71)
Hence we get
φ
i
=
1
4π
1
r
∂φ
i
∂n
0
+
∂φ
0
∂n
i
ds −
1
4π
φ
i
∂
∂n
0
1
r
+ φ
0
∂
∂n
i
1
r
ds
(10.72)
Now
∂
∂n
i
= −
∂
∂n
0
and on the surface φ
i
= φ
0
326 10 Green’s Theorem in Potential Theory
Therefore,
φ
i
=
1
4π
s
1
r
∂φ
i
∂n
0
−
∂φ
0
∂n
0
ds (10.73)
φ
0
=
1
4π
s
1
r
∂φ
i
∂n
0
−
∂φ
0
∂n
0
ds (10.74)
by adding the terms. Both values in (10.73) and (10.74) are exactly equal. If
φ
0
be the potential at any point outside a closed surface S due to masses inside
the surface and φ
i
is the potential at points inside the surface due to masses
outside and if φ
0
= φ
i
on the surface then the expression
1
4π
∂φ
i
∂n
−
∂φ
0
∂n
ds
r
has the value φ
0
at the external point and the value φ
i
at the internal points.
Here r denotes the distance from the point source at any po int on the surface.
n is the direction of the normal.
If in a closed surface S there are certain distribution of mass and if φ
i
is
harmonic inside and φ
0
is harmonic outside and if φ
i
= φ
0
on th e s urfa ce, then
there exists one and only one surface distribution for which φ
i
is the internal
potential and φ
0
is the external potential.
10.15 Vector Green’s Theorem
Tai (1992) first demonstrated that if we take
F=
P ×∇×
Q (10.75)
where
Pand
Q are two vectors. Applying the vector identity we get
∇.
F=(∇×
P).(∇×
Q) −
P.∇×∇×
Q (10.76)
Substituting these va lu es in Gauss’s divergence theorem we get
v
(∇×
P ) • (∇×
Q) −
P •∇×∇×
Q
dv =
s
(
P ×∇×
Q)ds =
s
⌢
n
.(
P ×∇×
Q)ds
(10.77)
where n denotes the outward normal unit vector on the surface.
By interchanging the role of
Pand
Q, the way it was done for scalar
Green’s function, and taking the difference of the two resultant equations, we
get the vector Green’s theorem of second symmetrical formula as
10.15 Vector Green’s Theorem 327
v
(
P.∇×∇×
Q −
Q.∇×∇×
P)dv
=
s
(
Q ×∇×
Q −
P ×∇×
Q)
ds
−
s
(n.(
Q ×∇×
P −
P ×∇×
Q) ds. (10.78)
