Салимов Р.Б. Математика (для студентов бакалавриата)

Подождите немного. Документ загружается.

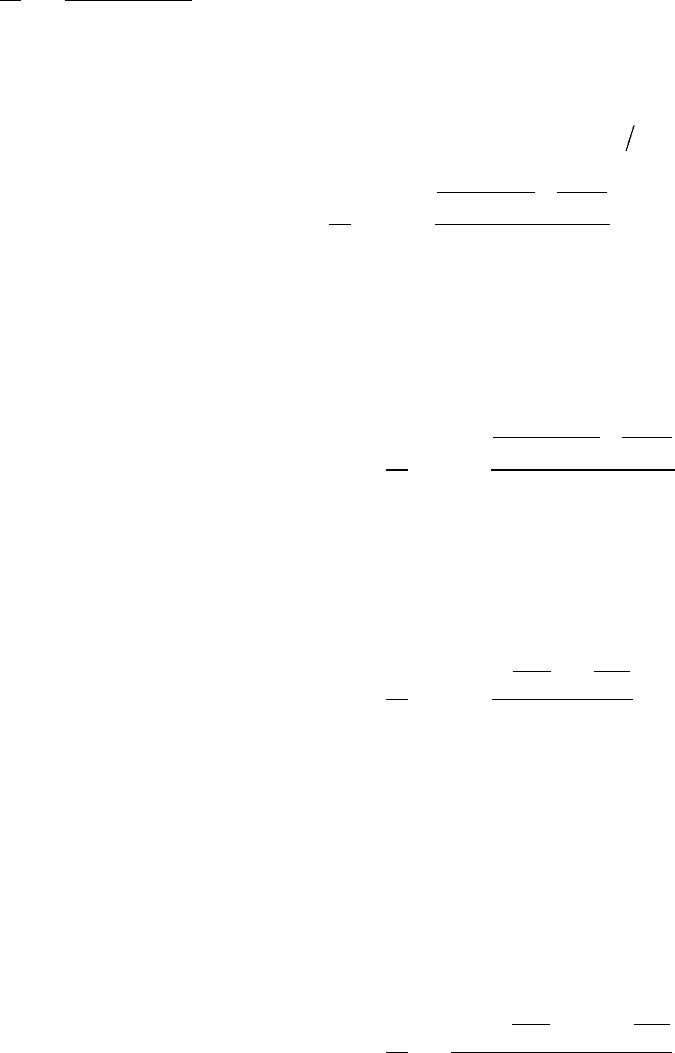
101

(b)

(c)

Доказательство. Докажем лишь последнее утверждение (c) ((a) и (b) до-

казываются аналогично).

По формуле (8), в которой вместо нужно взять , имеем

(9)

Разности это соответственно прира-

щения функций и Отсюда находим

Эти суммы подставим в (9) и получим

(10)

Выражение в числителе правой части этой формулы приведем к общему зна-

менателю и представим ее в виде

(11)

Предел правой части формулы (11) равен пределу числителя, делённому на

предел знаменателя. Но предел числителя равен разности пределов, так как

там стоит предел разности. Предел знаменателя равен сумме пределов слага-

емых, но здесь пределы берутся при когда следовательно, и

не изменяются, т. е. являются постоянными, и эти множители выносятся

за знак предела. Поэтому (11) примет вид

(12)

Так как – дифференцируемые функции, то существуют пределы

и Кроме того, по условию теоремы –

дифференцируемая функция, значит, она непрерывна, поэтому согласно вто-

( )

;UV U V UV

′

′′

⋅ = ⋅+⋅

U U V UV

′

′′

⋅−⋅







()fx

() ()Ux Vx

( ) ()

lim .

Ux x Ux

Vx x Vx

∆→

+∆

−

′

+∆





∆



( ) () ,Ux x Ux U+∆ − =∆

( ) ()Vx x Vx V+∆ − =∆

()Ux

( ).Vx

( ) ( ),Ux x U Ux+∆ =∆ +

( ) ( ).Vx x V Vx+∆ =∆ +

() ()

lim .

U Ux Ux

V Vx Vx

∆→

∆+

−

′

∆+





∆



lim .

V V VV

∆→

∆∆

−

′



∆∆



+∆



0,x∆→

( ),Ux

( ),Vx

lim lim

lim

V VV V

∆→ ∆→

∆→

∆∆

−

′



∆∆



+∆



( ),Ux

()Vx

lim( / )

UxU

∆→

′

∆ ∆=

lim( / ) .

VxV

∆→

′

∆ ∆=

()Vx

5354.ru

102

рому определению непрерывной функции Подставив последние

три предела в (12), получим формулу (с) .Теорема доказана.

Следствие из утверждения ( ) теоремы 3. Если

– постоянная,

()V Vx=

– дифференцируемая функция, то

() .cV cV

′′

В самом деле, когда , имеем , и формула ( ) теоремы

2 даёт

§ 6. Производные тригонометрических и логарифмической

функций

Теоремы 4 и 5 (производные синуса и косинуса). Если то

Если то Или коротко и

Доказательство. Докажем первую теорему (вторая доказывается анало-

гично).

Производная функции согласно формуле (8) равна

Числитель формулы справа можно разложить по из-

вестной из тригонометрии формуле разности синусов:

sin( ) sinxx x+∆ −

Подставив это выражение в предыдущую формулу,

получим Справа предел произведения равен

произведению пределов, поэтому

sin( /2)

lim lim cos( /2).

y xx

∆→ ∆→

∆

′

= ⋅ +∆

∆

(13)

Но первый предел равен единице, т. к. представляет собой «первый замеча-

тельный предел», в котором А второй предел, в силу непрерыв-

ности косинуса, при

0x∆→

/2xx x+∆ →

равен Подставив эти пределы

в формулу (13), получим то, что требуется. Теорема доказана.

Теоремы 6 и 7 (производные тангенса и котангенса). Если то

Если то Или коротко: и

lim 0.

∆→

∆=

constUc= =

0Uc

′′

= =

( )

.cV c V cV cV

′

′ ′′

⋅ = ⋅ +⋅ =⋅

sin ,yx=

cos .yx

′

cos ,yx=

sin .yx

′

= −

( )

sin cosxx

′

( )

cos sin .xx

′

= −

( ) siny fx x= =

sin( ) sin

lim .

xx x

∆→

+∆ −

′

∆

2sin( /2)cos( /2).x xx= ∆ +∆

sin( /2)cos( /2)

lim .

x xx

∆→

∆ +∆

′

∆

2 0.x

∆=→

cos .x

tg ,yx=

1 cos .

′

ctg ,yx=

1 sin .yx

′

= −

( )

tg 1 cosxx

′

( )

ctg 1 sin .xx

′

= −

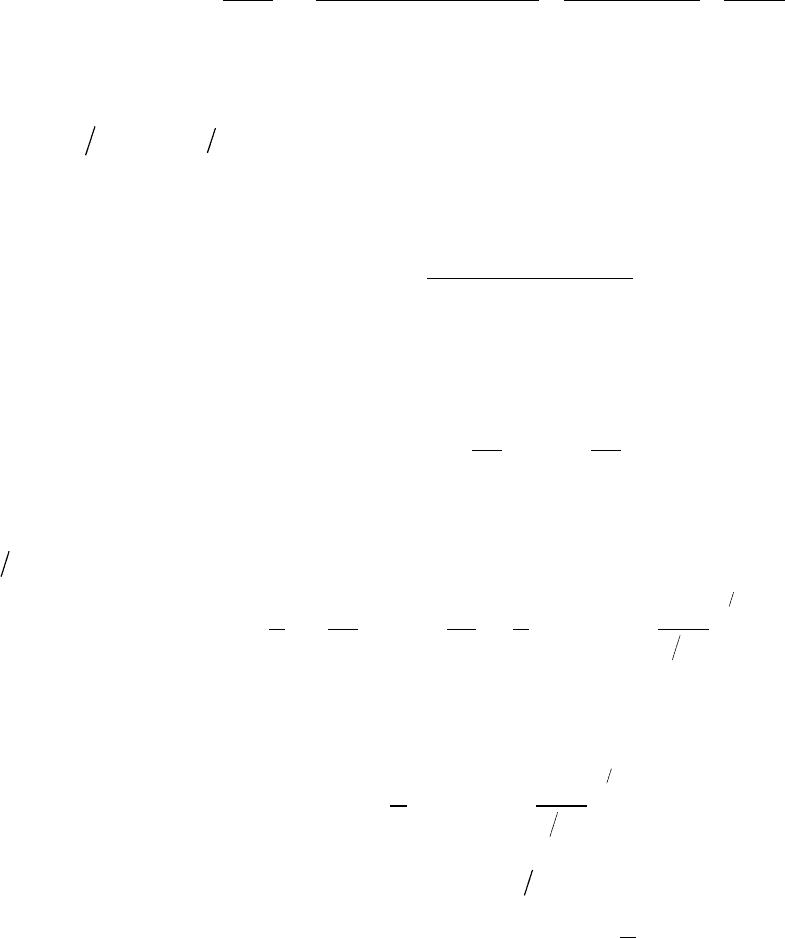
103

Доказательство. Докажем первую теорему (вторая доказывается анало-

гично). С учётом формулы ( ) теоремы 3 имеем

Теорема 8 (производная логарифмической функции). Если

то Или коротко:

Доказательство. Согласно определению производной

В числителе воспользуемся тем, что разность логарифмов равна логарифму

отношения, поэтому

Выражение под знаком предела разделим и умножим на затем множитель

вынесем за знак предела, так как он не зависит от Получим

Так как логарифм – непрерывная функция, знаки предела и логарифма можно

поменять местами, поэтому

При фиксированном

0x ≠

и имеем . Значит, согласно тео-

реме 17 главы 4 Поэтому . Пришли к утвер-

ждению теоремы.

В частности, при имеем и Тогда утвер-

ждение теоремы примет вид

( )

2 22

sin sin cos sin cos cos sin 1

tg .

cos cos cos cos

x xx x x x x

x x xx

′

′′

−+



′

= = = =





log ,

yx=

( )

1 ln 1 log .

y xa x e

′

= =

( )

log

′

1/( ln ) (log )/ .

xa ex= =

( )

log log

log lim .

xx x

∆→

+∆ −

′

∆

( )

log lim log 1 .

∆→

∆



′

= +



∆



1 x

.x∆

( )

log lim log 1 lim log 1 .

aa a

x x x x xx

∆

∆→ ∆→



∆1



′

= += +



∆∆



( )

log log lim 1 .

x xx

∆

∆→



′

= +



∆



0x∆→

xxx∆ = →∞



( )

lim 1 1/ .

∆→

→∞



( )

log log

′

ae=

ln ln 1ae= =

log log ln .

x xx= =

( )

ln 1/ .xx

′

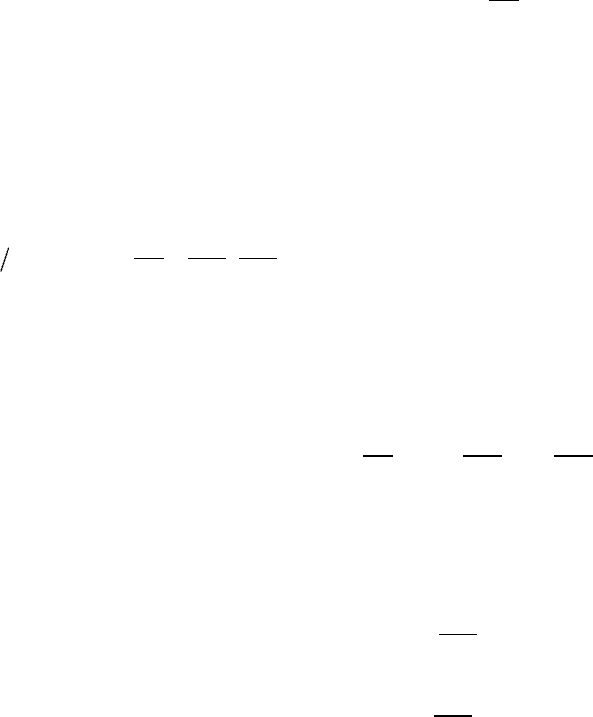
5354.ru

104

§ 7. Производная сложной функции

Теорема 9 (производная сложной функции). Если а

т. е. – сложная функция от

[ ]

( )

()yf x

, причём и – диффе-

ренцируемые функции, то справедлива формула

(14)

Доказательство. Приращению аргумента функции отвечает

приращение , а последнему приращению аргумента

функции отвечает приращение . Таким образом,

приращению аргумента в конечном счёте отвечает приращение рас-

сматриваемой сложной функции зависящей от Поэтому производная

этой сложной функции будет равна

(15)

Учтём, что так как функция является дифференцируемой, то, как бы-

ло доказано ранее, она является непрерывной, поэтому, согласно второму

определению непрерывности, для функции имеем Иначе

говоря, если Теперь, умножив и поделив на запишем от-

ношение в виде

В этом соотношении перейдём к пределу при (при этом ), кро-

ме того, учтём, что предел правой части равен произведению пределов. В

итоге получим

(16)

Так как функции и являются дифференцируемыми, то су-

ществуют конечные пределы

(17)

(18)

( )

,y fU=

( )

,Ux= ϕ

( )

xϕ

( ) ( ) ( )

y fUU fU x

′′ ′′ ′

= ⋅ = ⋅ϕ

x∆

( )

Ux= ϕ

( ) ( )

U xx x∆ =ϕ +∆ −ϕ

( )

y fU=

( ) ( )

y fU U fU∆ = +∆ −

x∆

y∆

lim .

∆→

∆

′

∆

( )

Ux= ϕ

( )

Ux= ϕ

lim

∆→

∆ = 0.

0,U∆→

0.x∆→

,U∆

yx∆∆

y yU

x Ux

∆ ∆∆

= ⋅

∆∆∆

0x∆→

0U∆→

0 00

lim lim lim .

x Ux

y yU

x Ux

∆→ ∆ → ∆→

∆ ∆∆

= ⋅

∆ ∆∆

( )

y fU=

()U fx=

( )

lim ,

∆→

∆

′

∆

( )

lim .

∆→

∆

′

= ϕ

∆

105

Согласно (16) из существования пределов (17) и (18) вытекает существование

предела (15). Производные (15), (17) и (18) подставим в (16) вместо соответ-

ствующих пределов и придём к формуле (14). Теорема доказана.

Например, пусть дана сложная функция т. е.

По формуле (14) имеем для производной этой сложной функции

Здесь поэтому Анало-

гично получается формула для дифференцирования сложной функции, состо-

ящей из трёх и большего числа составляющих функций. Запишем формулу

для дифференцирования сложной функции, состоящей из трех составляющих

функций.

Пусть Имеем сложную функцию

Её производная будет равна

Коротко правило дифференцирования сложной функции можно записать так:

производная сложной функции равна произведению производных её состав-

ляющих по своим аргументам.

§ 8. Производные степенной и показательной функций.

Логарифмическое дифференцирование

Теорема 10 (производная степенной функции). Если – лю-

бое действительное число, то или коротко:

() .

x nx

−

′

Доказательство. Пусть

0.x >

От соотношения , возьмём нату-

ральный логарифм: Далее продифференцируем эту функцию, при

этом показатель степени как постоянный множитель вынесем за знак про-

изводной: Отсюда

(19)

Здесь производная левой части есть производная сложной функции. Так как

логарифм зависит от который в свою очередь зависит от , то по формуле

(14) имеем Но поэтому

(20)

cos ,yU=

ln ,Ux=

cos(ln ).yx=

( )

cos (sin )/ .

y U U Ux

′

= ⋅=−

ln ,Ux=

( )

[sin ln ]/( ).

y xx

′

= −

( ),y fU=

( ),UV= ϕ

( ).Vx= ψ

( )

{ ]}.yf x= ϕ[ψ

( ) ( ) ( )

( ) ( ).

yx fUUV fU V x

′ ′ ′′ ′ ′ ′

= ⋅ ⋅ = ⋅ϕ ⋅ψ

yx=

0n ≠

y nx

−

′

yxn

= ≠

ln ln .yn x= ⋅

( ) ( )

ln ln .

y nx

′′

= ⋅

( )

ln / .

y nx

′

( ) ( )

ln ln .

y yy

′′

′

= ⋅

( )

ln 1 ,

′

( )

ln .

′

= ⋅

5354.ru

106

Это выражение подставим в левую часть (19) и получим или

Подставив сюда , получим то, что требуется. Теорема доказа-

на. При

1n =

теорема дает

( ) 1.

′

Доказательство теоремы проведено для случая

0.x >

Без обоснования от-

метим, что утверждение теоремы справедливо и для

0.x ≤

Замечание. При доказательстве теоремы соотношение сначала

прологарифмировали, взяв натуральный логарифм от него, а затем получен-

ное соотношение продифференцировали по Операция взятия логарифма и

последующего дифференцирования называется логарифмическим дифферен-

цированием, а выражение (20) называется логарифмической производной.

Теорема 11 (производная показательной функции). Если то

Или коротко:

Доказательство теоремы аналогично предыдущему. При

ae=

теорема да-

ет

() .

′

Наконец, отметим, что производные от степенно-показательных функций

вида находятся с помощью логарифмического дифференцирова-

ния. Вычислим, например, производную функции . Для этого пролога-

рифмируем, а затем продифференцируем обе части равенства . Получим

или . Далее, . С учетом (20) имеем

Отсюда

§ 9. Неявная функция и её производная

Функция называется неявной, если она определена соотношени-

ем, не разрешенным относительно :

(21)

где – известное выражение. Например, таковыми являются соотноше-

ния

, (22)

. (23)

Если соотношение (21) удаётся разрешить относительно то мы придём к

явному заданию. Например, из (22) следует Но такой переход не

y y nx

′

y ny x

′

yx=

ya=

ln .

ya a

′

( )

ln .

a aa

′

( )

[]

y Ux=

yx=

ln ln

yx=

ln lnyxx=

(ln ) ( ln )

y xx=

/ ( ln ) ,

yy xx=

(1 ln (1/ )).

y y xx x=⋅+

(ln 1).

yx x= +

( )

y fx=

( )

, 0,Fxy=

( )

,Fxy

10xy+ −=

xy e−+ =

1.yx=±−

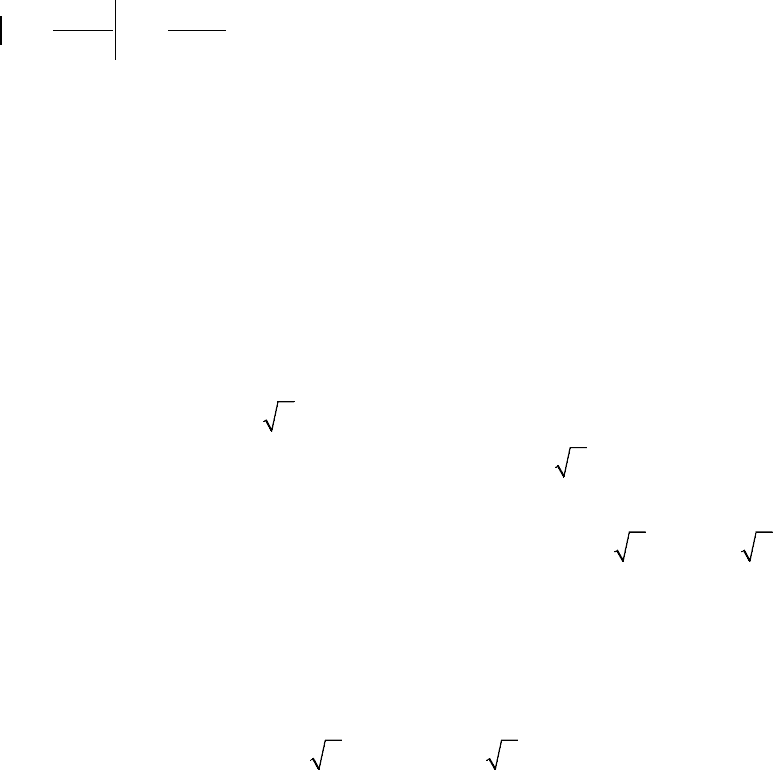
107

всегда возможен, например, в случае функции, заданной уравнением (23).

Однако всегда можно найти производную неявной функции. Для этого доста-

точно соотношение (21) продифференцировать по помня, что в нём есть

функция от Сделаем это применительно к функции, определённой неявно

формулой (23). Соотношение (23) продифференцируем по учитывая, что

слагаемое – произведение двух функций, а слагаемое – сложная функ-

ция. Получим Отсюда найдем искомую производную

(24)

В этой формуле – значение функции, соответствующее взятому , согласно

(23). В частности, из соотношения (23) видно, что значению отвечает

значение т. к. при этих значениях соотношение (23) выполняется. По-

этому при производная согласно (24), будет равна

§ 10. Обратная функция и ее производная

Пусть дана функция . Выразим из этого соотношения через и

получим где – аргумент, а – функция. Эта последняя функция

называется обратной к функции Ясно, что на плоскости этим

функциям отвечает один график, так как они представляют собой разные

формы записи одной и той же зависимости. Например, для функции

обратной является Здесь каждому значению отвечают два значе-

ния В этом случае говорят, что функция является многозначной. В

данном случае она двузначна. Ясно, что из этой двузначной функции можно

получить две однозначные функции, а именно, и Эти одно-

значные функции называются ветвями рассматриваемой многозначной

функции. В дальнейшем всегда в случае многозначной обратной функции

()xy

под обратной функцией будем понимать какую-либо выбранную

нами однозначную её ветвь. Например, для функции в качестве обрат-

ной можно взять либо , либо по нашему усмотрению. Функ-

ции отвечает парабола (рис. 49).

1 0.

y xy e y

′′

⋅+⋅ + ⋅ =

/( ).

y yxe

′

=−+

0x =

0,y =

0x =

′

xe e

−

′

= = =

( )

y fx=

( )

,xy= ϕ

( )

.y fx=

Oxy

yx=

.xy= ±

xy= ±

xy= +

.xy= −

yx=

xy= +

xy= −

yx=

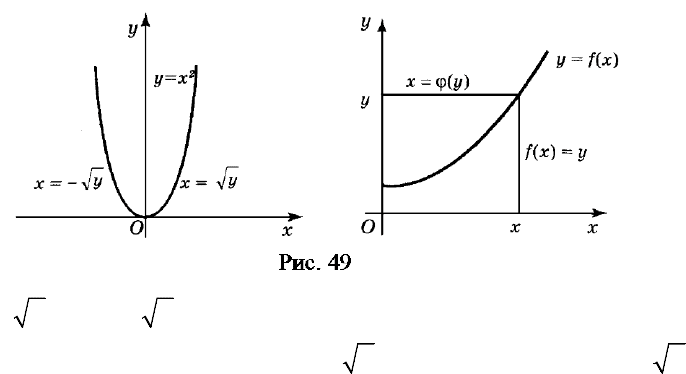
5354.ru

108

Функциям и отвечают соответственно правая и левая части

параболы, для которых (в случае ) и (в случае ).

Отметим следующий геометрически очевидный факт: если график функ-

ции является восходящей (нисходящей) кривой, т. е. с увеличением

абсциссы точки кривой её ордината увеличивается (уменьшается),

то обратная к ней функция

()xy

существует и будет однозначной, так как

каждому значению из области значений функции отвечает лишь

одно значение обратной функции

( ).xy

В предыдущем примере для функции это условие нарушается, так

как кривая состоит из двух частей: одна является нисходящей, а другая

восходящей.

Теорема 12 (о производной обратной функции). Если

()xy

– функ-

ция, обратная по отношению к функции , и

( ) 0,y

′

≠

то

(25)

или коротко:

Доказательство. Соотношение

()xy

определяет функцию, обратную к

поэтому Полученное соотношение продифференцируем

по помня, что в правой части стоит сложная функция. Тогда будем иметь

′′

Отсюда

′′

или

§ 11. Производные обратных тригонометрических функций

Функция

Arcsinyx=

является обратной по отношению к функции

График функции совпадает с графиком функции

Arcsinyx=

. Для лю-

бого из интервала на графике функции

Arcsinyx=

(рис. 50) имеется

бесчисленное множество точек с абсциссой их ординаты – значения функ-

ции. Следовательно, эта функция является бесконечнозначной. Возьмём ту

xy= +

xy= −

0x ≥

xy= +

0x <

xy= −

( )

y fx=

( )

y fx=

( )

y fx=

yx=

( )

y fx=

( )

( ) 1/fx y

′′

1/ .

′′

( )

,y fx=

( )

x fx

= [ ].

1/ .

′′

sin .xy=

sinxy=

11x−≤ ≤

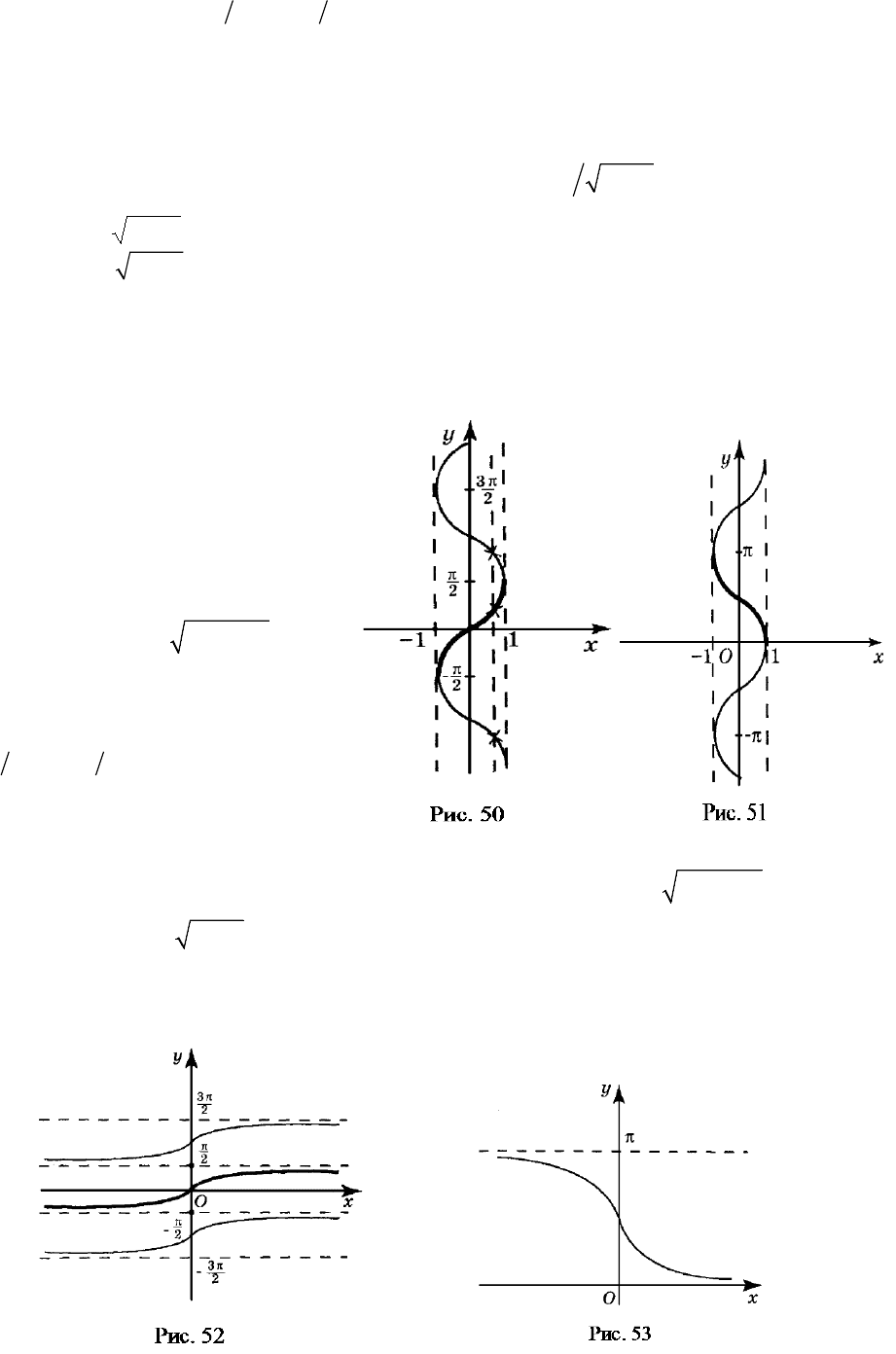
109

часть графика, где ; на этом участке для каждого из интервала

имеется лишь одна точка с абсциссой В дальнейшем под функцией

rcsinyA x=

всегда будем понимать ветвь функции, значения которой лежат в

интервале

/2 /2y

ππ

− ≤≤

и обозначать её

xy arcsin=

Теорема 13. Если то или коротко:

Доказательство. Производная функции равна Так как

функция – обратная к то согласно (25) имеем

(26)

Мы нашли искомую производ-

ную, но пока она выражена че-

рез а не через Но

следовательно, нужно

выразить через Как из-

вестно, но

функция принимает

значения из интервала

Для таких как

мы знаем, следова-

тельно, в предыдущей формуле

мы должны оставить знак «+». Таким образом, . Так как

то Подставив это выражение в (26), получим утвержде-

ние теоремы 13.

Функция

Arccosyx=

– обратная по отношению к функции (см.

22y

ππ

− ≤≤

[ 1; 1]−

arcsin ,yx=

11yx

′

= −

( )

arcsin 1/ 1 .xx

′

= −

sinxy=

cos .

′

arcsinyx=

sin ,xy=

1/cos .

′

sin ,xy=

cos y

sin .yx=

cos 1 sin ,yy=±−

arcsinyx=

2 2.y

ππ

− ≤≤

cos 0,y ≥

cos 1 sinyy=+−

sin ,yx=

cos 1 .yx= −

cosxy=

5354.ru

110

рис. 51) В дальнейшем всегда под функцией будем понимать одно-

значную ветвь функции

Arccosyx=

, значения которой лежат в интервале

0.y

≤≤

Для этой функции справедлива следующая

Теорема 14. Если , то или коротко:

(arccos ) 1/ 1 .

′

=−−

Доказательство проводится аналогично предыдущему.

Функция

Arctgyx=

является обратной по отношению к функции

(см. рис. 52). Выберем её однозначную ветвь, для которой В

дальнейшем эту ветвь будем обозначать . Для нее справедлива

Теорема 15. Если то или коротко:

Доказательство проводится по аналогии с доказательством теоремы 13.

Функция

Arcctgyx=

является обратной по отношению к функции .

Выберем её однозначную ветвь, значения которой лежат в интервале

(рис. 53). Обозначим эту ветвь

.y arcctgx=

Для этой функции справедлива

Теорема 16. Если то или коротко:

Доказательство проводится по той же схеме, что и в случае теоремы 13.

§ 12. Функция, заданная параметрически,

и ее дифференцирование

Даны две дифференцируемые функции

. (27)

Аргумент будем называть параметром, пусть он изменяется в интервале

На плоскости возьмём точку коорди-

наты кото-рой вычисляются по формуле

(27). Если изменяется, то изменяются и коорди-

наты , и точка опи-сывает некоторую ли-

нию (см. рис. 54). В этом случае соот-ношения

(27) называют парамет-рическими уравнениями

указанной линии. Из первого уравнения (27) выразим через и получим

arccosyx=

′

=−−

tgxy=

2 2.y

ππ

− <<

arctgyx=

arctg ,yx=

( )

′

= +

( )

arctg 1/(1 ).

′

= +

ctgxy=

0 y

arcctg ,yx=

( )

′

=−+

( )

arcctg 1/(1 ).

′

=−+

( ) ( )

,x ty t=ϕ=ψ

αβ

≤≤

Oxy