Салимов Р.Б. Математика (для студентов бакалавриата)
Подождите немного. Документ загружается.

91
(рис. 43). На кривой отметим точку с абсциссой , её ордината равна ,
т. е. . На этой же кривой возьмём точку с абсциссой , её ор-
дината равна , т. е. . Когда абсцисса точки стремится к
– абсциссе точки , ордината точки стремится к согласно (16)
в силу непрерывности функции. Это означает, что при этом точка стре-
мится к точке , и графиком функции является сплошная линия без
разрывов.
Обозначим величину и назовём ее приращением аргумента рас-
сматриваемой функции . Разность соответствующих значений функции
обозначим
(17)
или, так как , , и назовём приращением функции
, вычисленным для точки и соответствующим приращению аргу-
мента..
В (16) учтём, что , т. к. предел постоянной равен этой посто-
янной. Этот предел подставим в правую часть (16), затем его перенесём влево
и учтём, что разность пределов равна пределу разности. После этого получим
. Но разность под знаком предела, согласно (17), равна .
Поэтому имеем
. (18)
Здесь мы учли, что при разность . Таким образом, если функция
непрерывна в точке , то при стремлении приращения аргумента к нулю,
соответствующее приращение функции, вычисленное для точки , стремится
к нулю. Проведя рассуждения в обратном порядке, получим, что из (18) сле-
дует (16).
Соотношение (18) иногда называют вторым определением непрерывно-
сти функции в точке. Оно равносильно исходному определению (16).
§ 15. Свойства непрерывных функций
Теоремы 18 (и 19). Алгебраическая сумма (и произведение) конечного
числа функций, непрерывных в точке, есть функция, непрерывная в этой
точке.
0
M
c
()fc
( )
0
, ()M c fc
M
x
()fx
( )
, ()Mx fx
x
M
c
0
M
()fx
M
()fc
M
0
M
()y fx=
xc x−=∆
()fx
() ()fx fc y−=∆
xc x= +∆
( ) ()fc x fc y+∆ − =∆
()fx
c
x∆
() lim ()
xc
fc fc
→
=
[ ]
lim ( ) ( ) 0
xc
fx fc
→
−=
y∆
0
lim 0
x
y
∆→
∆=
xc→
0x∆→
c
x∆
c
5354.ru
92
Теорема 20. Частное от деления двух функций, непрерывных в точке,
есть функция, непрерывная в этой точке, если знаменатель в ней не обраща-
ется в нуль.
Эти теоремы доказываются, исходя из определения непрерывности функ-
ции (16), с привлечением ранее доказанных теорем о пределе суммы, произ-
ведения и частного. На этом не останавливаемся.
Теорема 21. Сложная функция, состоящая из непрерывных функций,
есть функция непрерывная.
Доказательство. Теорему докажем для сложной функции, состоящей из
двух функций. В случае большего числа образующих функций теорема дока-
зывается аналогично.
Пусть дана функция , в которой , в свою очередь, является
функцией от ( ), т. е. дана сложная функция
. (19)
Пусть значению аргумента отвечает значение функции ,
т. е. . Кроме того, известно, что функция непрерывна в точке
, т. е. согласно (16)
. (20)
Дано также, что функция непрерывна в точке , соответствующей
точке , т. е. . Последняя формула показывает, что при
имеем , а так как , , то . Нужно доказать, что
сложная функция (19) непрерывна в точке , т. е. нужно показать, что
. Действительно, с учетом (19) имеем
.
Теорема доказана.
Теорема 22. Всякая основная элементарная функция непрерывна в каж-
дой точке, в которой она определена.
Эта теорема принимается без доказательства.
Из теорем 18 – 22 и определения элементарной функции вытекает, что
элементарные функции непрерывны в каждой точке, в которой они определе-
ны. Отсюда в соответствии с (16) следует, что предел элементарной функции
()y fU=
U
x
()Ux
ϕ
=
[ ]
(()) ()y f x Fx
ϕ
= =
xc=
Up=
()Ux
ϕ
=
()pc
ϕ
=
()y fU=
p
lim ( ) ( )
Up
fU f p
→
=
()Ux
ϕ
=
c
p
lim ( ) ( )
xc
xc
ϕϕ
→
=
xc→
() ()xc
ϕϕ
→
()Ux
ϕ
=
()pc
ϕ
=
Up→
c
lim ( ) ( )
xc
Fx Fc
→
=
[ ] [ ] [ ]
lim ( ) lim ( ( )) lim ( ) ( ) ( ) ( )
xc xc U p
Fx f x fU f p f c Fc
ϕϕ
→→ →
= = = = =

93
можно вычислить подстановкой предельного значения аргумента. Например,
.
§ 16. Точки разрыва функции
Точка называется точкой разрыва функции , если в ней
нарушается хотя бы одно из трёх условий непрерывности функции в точке,
указанных в параграфе 14.
В качестве примера возьмём функцию, определённую формулой
. (21)
Ясно, что эта функция определена везде, кроме точки . Для любого по-
ложи-тельного имеем и согласно формуле (21)
. Если же , то и . График
этой функции изображен на рис. 44.
Так как функция в точке не определена, то на
её графике нет точки с абсциссой , т. е. нет точки,
лежащей на оси , поэтому график как бы не доходит
до оси , что отмечено стрелками. Для любой точки
имеем . Кроме того, для любого имеем , поэтому
. Это означает, что функция в точке непрерывна в силу
(16). Аналогично установим, что для любого функция также непре-
рывна. Но точка есть точка разрыва функции (21) по двум причинам:
• не существует , т. к. в точке функция (21) не определена;
• для функции (21) не существует предел
.
В самом деле, предел справа этой функции
, а предел слева . Таким
образом, односторонние пределы хотя и суще-
ствуют, но не равны друг другу, значит, не суще-
ствует обычный (двусторонний) предел .
Точка называется точкой разрыва перво-
го рода функции , если существуют конечные односторонние пределы
и . Например, для функции (21) точка – точка разрыва
22
/2
lim (sin ) sin ( /2) 1
x
x
π
π
→
= =
xc=
()y fx=
( ) | |/fx x x=
0x =
x
xx=
() 1fx=
0x <
xx= −
() 1fx= −
0x =
0x =
Oy
Oy
0xc= >
() 1fc=
0x >
() 1fx=
lim ( )
xc
fx
→
=
() 1fc=
c
0xc= <
0x =
(0)f
0x =
0
lim ( )
x
fx
→
00
lim ( ) 1
x
fx
→+
=
00
lim ( ) 1
x
fx
→−
= −
0
lim ( )
x
fx
→
xc=
()y fx=
0
lim ( )
xc
fx
→−
0
lim ( )
xc
fx
→+
0x =

5354.ru
94
первого рода. Все остальные точки разрыва называются точками разрыва
второго рода. Для функции (рис. 45) точкой разрыва второго рода
будет , так как в этой точке функция не определена и односторонние
пределы бесконечны: и .
() 1fx x=
0x =
00
lim ( )
x
fx
→+
=+∞
00
lim ( )
x
fx
→−
=−∞

95
ГЛАВА 5. ПРОИЗВОДНЫЕ ФУНКЦИИ ОДНОГО
ПЕРЕМЕННОГО
§ 1. Задача об определении скорости
Пусть точка движется по прямой неравномерно и проходит путь от точки
до точки длиной за время (рис. 46). С изменением длина пути
изменяется по заданному закону (т. е. функцию считаем за-
данной). Итак, . В следующий момент времени , ,
точка окажется в положении . Таким образом,
за время точка пройдёт путь, равный
(получаемый из формулы заме-
ной на ). Это означает, что за время
точ-
Рис. 46 ка проходит путь
.)()(
1
StfttfMM ∆=−∆+=
(1)
Путь равен приращению функции , соответствующему при-
ращению и вычисляемому для точки . Ясно, что отношение харак-
теризует скорость передвижения точки на участке за время . Чем
быстрее точка движется, тем больший путь она пройдёт за время , тем
больше будет значение этого отношения. Нас интересует скорость движения
точки не на всём участке (не за весь промежуток времени ), а скорость
движения точки в положении (в момент ).
Очевидно, что чем меньше , тем лучше отношение характеризует
скорость движения точки в момент . Эту последнюю скорость наиболее
полно характеризует предел , который обозначается . Итак,
или с учётом (1)
. (2)
0
M
M
S
t
t
S
()S ft=
()S ft=
0
()MM S f t= =
tt+∆
0t∆>
1
M
tt+∆
()ft t+∆
()S ft=
t
tt+∆
t∆
1
MM
()S ft=
t∆
t
St∆∆
1
MM
t∆
t∆
1
MM
t∆
M
t
t∆
St∆∆
t
0
lim( / )
t
St
∆→
∆∆
()V Vt=
()V Vt= =
0
lim( / )
t
St
∆→
∆∆
0
( ) ()
( ) lim
t
ft t ft
V Vt
t
∆→
+∆ −
= =
∆

5354.ru
96
§ 2. Определение, механический и геометрический смыслы
производной
Дана функция . Приращению
x∆
аргумента этой функции отвеча-
ет её приращение , записанное для точки . Возьмём от-
ношение
.
Предел этого отношения при называется производной от функции
в точке и обозначается . Итак,
(3)
или
. (4)
Понятно, что в каждой точке эта производная будет своя, поэтому произ-
водная также является функцией от . Для обозначения производной
применяются также символы . Значение производной в конкрет-
ной точке обозначается или . Отметим, что операция нахож-
дения производной называется дифференцированием. Например, для функ-
ции имеем
22
0
( ) ()
( ) lim 2 .
x
xx x
fx x
x
∆→
+∆ −
′
= =
∆
.
При прямолинейном движении точки по закону скорость точки в
момент определяется формулой (2):
00
( ) ()
( ) lim lim .
tt
S ft t ft
V Vt
tt
∆→ ∆→
∆ +∆ −
= = =
∆∆
Сравнив ее с формулами (3), (4), заключаем, что в правой части (2) стоит вы-
ражение, равное . Итак, скорость точки в момент равна произ-
водной от пути по времени . В этом состоит механический смысл произ-
водной.
Выясним теперь геометрический смысл производной. Пусть дана
функция . Изобразим её график на плоскости и на кривой
()y fx=
( ) ()y fx x fx∆ = +∆ −
x
( ) ()y fx x fx
xx
∆ +∆ −
=
∆∆
0x∆→
()y fx=
x
()fx
′
0
( ) lim
x
y
fx
x
∆→
∆
′
=
∆
0
( ) ()
( ) lim
x
fx x fx
fx
x
∆→
+∆ −
′
=
∆
x
()fx
′
x
,y
′
,
x
y
′
/dy dx
xa=
()fa
′
y
xa
′
=
2
()fx x=
()S ft=
t
()
t
ft S
′′
=
V
t
S
t
()y fx=
Oxy
()y fx=
97
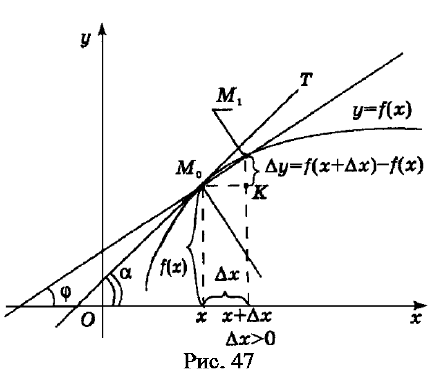
возьмём точки и (рис. 47 сделан для случая,
когда и , а если , то точка будет лежать левее точки
). Через точки , проведём секущую для графика данной функции.
Эта секущая образует с осью угол . Пусть
K
- точка с абсциссой
xx+∆
и
ординатой
( )
.fx
Из рис. 47 видно, что для треугольника справедливо
соотношение
. (5)
Если при стремлении точки к точке с любой стороны секущая
стремится к определённому положению , то эта прямая называется
касательной к кривой в её точке .
Пусть – угол, образованный этой касательной с осью , тогда при
точка стремится к , стремится к и угол стремится
к углу . Так как – непрерывная функция, то . Перейдём в
(5) к пределу при , тогда . Предел в правой части
равен , а согласно (3) предел в левой части последней формулы равен
, поэтому .
Итак, вычисленная в точке производная от функции равна ,
причём угол образован с осью касательной к кривой в её точке
с абсциссой . В этом заключается геометрический смысл производной.
Иначе говоря, эта производная равна угловому коэффициенту каса-
тельной.
( )
0
, ()M x fx
( )
1
,( )Mxxfxx+∆ +∆
0x∆>
x xx+∆ >
0x∆<
1
M
0
M
0
M
1
M
Ox
ϕ
01
M KM
/ tgyx
ϕ
∆ ∆=
1
M
0
M
01
MM
0
MT
0
MT
()y fx=
0
M
α
Ox
0x∆→
1
M
0
M
01
MM
0
MT
ϕ
α
tg
ϕ
limtg tg
ϕα
ϕα
→
=
0x∆→
00
lim( / ) lim tg
xx
yx
ϕα
ϕ
∆→ ∆→
→
∆∆=
tg
α
()fx
′
( ) tgfx
α
′
=
x
()y fx=
tgα
α
Ox
()y fx=
0
M
x
tgk
α
=
5354.ru
98
§ 3. Касательная и нормаль к кривой.
Существование производной
Пусть – фиксированная точка кривой , т. е. и
– известные числа. Найдем производную
( )
fx
′
и вычислим
( )
0
f x tg
α
′
=
- угловой коэффициент касательной к кривой в точке
0
.M
Зная ко-
ординаты точки и угловой коэффициент касательной, запишем уравнение
касательной (см. формулу (31) главы 2):
.
Прямая, проходящая через точку перпендикулярно к касательной,
называется нормалью к кривой в точке
. В силу перпендикулярности нор-мали и
касательной угловой коэффициент этой нор-
мали ра-вен , поэтому урав-нение
нормали запишется так:
.
Например, запишем уравнения касательной
и нормали к кривой в её точке : и
соответственно, учитывая, что .
Если при стремлении к с одной стороны (для ) секущая
стремится к одному положению, а при стремлении к с другой
стороны (для ) эта секущая стремится к другому положению, то в точке
касательная к данной кривой не существует. Ясно, что кривая в
этом случае в точке имеет излом. При этом в точке не существует
производная , вычисляемая по формуле (3).
В самом деле, при , когда , отношение стремится к од-
ному пределу, а при , , это отношение стремится к другому пре-
делу, т. е. это отношение имеет разные односторонние пределы при .
Это означает, что обычный двусторонний предел (3) не существует, т. е. в
точке с абсциссой не существует производная . Последние рассуж-
дения проиллюстрируем на следующем примере.
Пусть функция определена формулой
000
(,)Mxy
()y fx=
0
x
00
()y fx=
0
M
0
MT
0 00
( )( )y y fx xx
′
−= −
0
M
()y fx=
0
M
0
1/ '( )fx−
00
0
1
()
()
yy xx
fx
−=− −
′
2
yx=
0
(1, 1)M
1 2( 1)yx−= −
1 ( 1/ 2)( 1)yx−=− −
'(1) 2f =
1
M
0
M
0x∆>
01
MM
1
M
0
M
0x∆<
0
M
()y fx=
0
M
0
M
()fx
′
0x∆→
0x∆>
yx∆∆
0x∆→
0x∆<
0x∆→
0
M
x
()fx
′
()y fx=
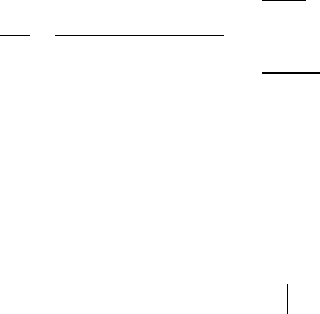
99
и имеет график, показанный на рис. 48. В качестве точки возьмём начало
координат . Тогда , , , . Здесь
имеем
Поэтому
Следовательно, предел слева (когда ) , а предел справа
(когда ) . Эти односторонние пределы не рав-
ны, следовательно, не существует двусторонний предел
)./(lim
0
xy
x
∆∆
→∆
Это озна-
чает, что не существует производная .
Для графика рассматриваемой функции секущая при с
разных сторон (для и для соответственно) стремится к разным
положениям ( при , при ), в точке график имеет
излом.
§ 4. Дифференцируемость функции
Функция называется дифференцируемой в точке если в
этой точке она имеет производную Иначе говоря, существует предел
),/(lim)('
0
0
xyxf
x
∆∆=
→∆
(6)
здесь
(7)
Если функция дифференцируема в каждой точке интервала, то её
называют дифференцируемой в этом интервале.
Теорема 1. Если функция дифференцируема в точке то
она непрерывна в этой точке.
2
0,
()
0
x при x
fx
x при x
−<
=
≥
0
M
O
0x =
xxx+∆ =∆
( ) (0) 0fx f= =
()fx x+∆ =
()fx∆
( )
2
0,
()
0.
x при x
fx
x при x
−∆ ∆ <
∆=
∆ ∆≥
( )
2
1 0,
( ) ()
0.
x
при x
x
y fx x fx
xx
x
x при x
x
−∆
=− ∆<
∆
∆ +∆ −
= =
∆∆
∆
=∆ ∆≥
∆
0x∆<
00
lim ( / ) 1
x
yx
∆→−
∆∆=−
0x∆≥
00 00
lim ( / ) lim ( ) 0
xx
yx x
∆→+ ∆→−
∆∆= ∆=
0
()
x
fx
=
′
01
MM
10
MM→
0x∆<
0x∆≥
Ox
0x∆≥
01
MM
0x∆<
0
()OM
()y fx=
0
,xx=
( ).fx
′
00
( ) ( ).y fx x fx∆ = +∆ −
()y fx=
()y fx=
0
,xx=

5354.ru
100
Доказательство. Приращение функции в точке , соответ-
ствующее приращению и определяемое формулой (7), запишем так:
В этом соотношении перейдём к пределу при при этом
учтём, что предел правой части равен произведению пределов сомножителей:
В правой части первый предел, согласно (6), су-
ществует и равен
0
()fx
′
(в силу условий теоремы, так как функция в точке
дифференцируема). Поэтому Но значит,
Согласно второму определению непрерывности функции в точке
это означает, что в точке функция непрерывна. Теорема доказана.
Отметим, что утверждение, обратное утверждению теоремы, не справед-
ливо, т. е. нельзя утверждать следующее: если функция непрерывна в точке,
то она дифференцируема в этой точке. Сказанное продемонстрируем на при-
мере функции Она непрерывна в точке , так как является
основной элементарной функцией (степенной функцией), и в точке
определена (равна нулю). Производная этой функции, как будет показа-
но дальше, равна . Но эта производная в точке не существует, т. е.
функция в этой точке не дифференцируема, хотя и непрерывна.
§ 5. Производная постоянной. Правила дифференцирования
Здесь при доказательстве теорем будем исходить из определения произ-
водной, согласно которому для функции производная выражается
формулой
(8)
Теорема 2. Производная постоянной равна нулю, т. е. если
( ) const,y fx= =
то или коротко
Доказательство. Для этой функции согласно (8) имеем
Теорема доказана.
Теорема 3. Если и – дифференцируемые функции, то:
(a)
()y fx=
0
xx=
x∆
( / ).y y xx∆=∆ ∆ ∆
0,x∆→
0
lim
x
y
∆→
∆
0
lim ( / )
x
yx
∆→
= ∆∆
0
lim .
x
x
∆→
⋅∆
0
x
0
00
lim ( ) lim .
xx
y fx x
∆→ ∆→
′
∆= ⋅ ∆
0
lim 0,
x
x
∆→
∆=
0
lim 0.
x
y
∆→
∆=
0
x
()y fx=
3
() .y fx x= =
0
0x =
0
0x =
()fx
′
2/3
/3x
−
0
0x =
()y fx=
0
( ) ()
( ) lim .
x
fx x fx
y fx
x
∆→
+∆ −
′′
= =
∆
0y
′
=
0.c
′
=
0 0 00
( ) () 0
lim lim lim lim 0 0.
x x xx
fx x fx c c
y
x xx
∆→ ∆→ ∆→ ∆→
+∆ − −
′
= = = = =
∆ ∆∆
()Ux
()Vx
( ) ( )
,;UVUVUVUV
′′
′′ ′′
+=+ −=−
