Салимов Р.Б. Математика (для студентов бакалавриата)
Подождите немного. Документ загружается.


11
Оси координат
Ox
и
Oy
на плоскости образуют систему координат
.Oxy
Пусть
1
M
,
2
M
– проекции точки
A
на оси
Ox
и
Oy
(рис. 2). Они являются ос-
нованиями перпендикуляров, опущенных из точки
A
на оси
Ox
и
Oy
соответ-
ственно. Пусть
x
и
y
- координаты точек соответственно
1
M
и
2
.M
Числа
x
и
y
называются координатами точки
A
на плоскости. Этот факт записывают в
виде
( , ).Axy
Плоскость указанной системы координат обозначают
2
R
. Опи-
санные выше системы координат в пространстве и на плоскости называют
прямоугольными декартовыми. Система координат, изображенная на рис. 2,
называется правой.
Полярные координаты на плоскости. Возьмем на
плоскости положительную полуось
Ox
, т. е. ту часть
оси, где
x
неотрицателен. Пусть
A
– произвольная точ-
ка плоскости и
ρ
– расстояние от точки
A
до начала
,O
θ
– угол, образованный отрезком
OA
с осью
Ox
, отсчи-
тываемый от оси
Ox
в направлении против хода часо-
вой стрелки, причём
02
θπ
≤<
(рис. 3). Числа
θ
и
ρ
называются полярными координатами точки
A
, при-
чем
ρ
– полярный радиус,
θ
– полярный угол,
O
– полюс, положительная по-
луось
Ox
– полярная ось.
Пусть
Oxy
– декартова система координат в рассматриваемой плоскости,
,xy
– декартовы координаты точки А. Из рис. 3 видно, что
cos , sinxy
ρ θ ρθ
= =
. Эти формулы выражают декартовы координаты точки
A
через её полярные координаты.
§ 3. Векторы, линейные операции над ними
Скалярной называется величина, которая полностью определяется своим
численным значением. Примерами скалярных величин являются длина, пло-
щадь, объём, масса.
Вектором называется направленный отрезок прямой,
соединяющий две точки в пространстве (рис. 4). Если А и
В – начало и конец вектора, то он обозначается или
.
Длиной (модулем) вектора называется число, равное
длине отрезка, соединяющего начало и конец вектора. Длина вектора
AB
a AB=
a AB=
Рис. 3

5354.ru
12
обозначается
AB AB=
или
.aa=
Если начало вектора совпадает с концом, то
вектор называется нулевым и обозначается
O
.
Векторы и называются коллинеарными, если они расположены на од-
ной прямой или на параллельных прямых. Векторы и называют равными
(в этом случае пишут ), если:
• равны их длины (
| || |ab=
);
• они коллинеарны;
• сонаправлены.
Следовательно, при параллельном переносе вектора получим вектор, равный
исходному.
Сложение векторов. Даны векторы и . Вектор перенесём парал-
лельно самому себе и поместим его начало в конец вектора . Тогда вектор,
начало которого совпадает с началом вектора , а конец – с концом вектора
, называется суммой векторов и и обозначается + . Ясно, что сумму
двух векторов можно получить иначе: построить , с началом в общей точ-
ке, затем достроить на этих векторах, как на сторонах, параллелограмм. Тогда
его диагональ, выходящая из общего начала, будет суммой исходных векто-
ров (см. рис. 5).
Указанный метод легко распространяется на случай трёх и большего чис-
ла векторов: от конца первого строим второй, от конца второго – третий и
т. д., тогда вектор, начало которого совпадает с началом первого, а конец – с
концом последнего, и будет суммой рассматриваемых векторов (рис. 6).
Свойства сложения векторов:
+ = + ; + ( + ) = ( + ) + ; +
O
= .
Эти свойства проверяются с помощью построения.
Разность векторов. Даны векторы и . Построим эти
векторы с началом в общей точке. Тогда вектор, начало ко-
a
b
a
b
ab=
a
b
b
a
a
b
a
b
a
b
a
b
Рис. 6
a
b
b
a
a
b
с
a
b
с
a
a
a
b
13
торого совпадает с концом вектора , а конец – с концом вектора , называ-
ется разностью векторов , и обозначается (рис. 7). Из рисунка вид-
но, что +( )= .
Умножение вектора на число. Даны вектор и число . Произведением
вектора на число называется вектор = = , который:
• коллинеарен ;
• имеет длину | | = | |⋅| |;
• направлен так же, как и , при , и противоположно – при
Свойства умножения вектора на число:
• ( )⋅ = ⋅ + ⋅ ;
• ⋅( + ) = ⋅ + ⋅ ;
• ( ⋅ )⋅ = ⋅(µ⋅ )= ⋅( ⋅ ).
Эти свойства доказываются с помощью построения.
Приведем еще одно соотношение. Пусть дан вектор и
– вектор, кото-
рый коллинеарен , направлен, как , и | | = 1. Он называется единичным.
Рассмотрим произведение | | вектора на длину вектора . По определе-
нию это есть вектор, который:
• коллинеарен вектору , следовательно, и ;
• имеет длину, равную длине вектора , так как | |⋅| | = | |;
• направлен, как и как , поскольку множитель | | – число положи-
тельное.
Таким образом, мы получили вектор, равный . Итак,
= | | (1)
§ 4. Проекция вектора на ось
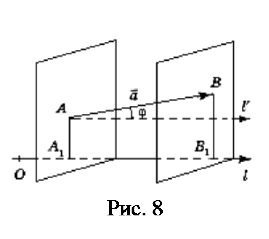
Пусть в пространстве задана некоторая числовая (координатная) ось l с
началом в точке
;O
= есть вектор, произвольно расположенный в про-
странстве (рис. 8). Пусть
1
A
и – проекции на ось l
соответственно начала
A
и конца
B
рассматриваемого
вектора (т. е.
1
A
и – точки пересечения с осью
l
пло-
скостей, перпендикулярных к оси
l
и проведенных че-
рез точки и ); и – соответственно коорди-
наты точек и на координатной оси Разность
b
a
a
b
a
−
b
b
a
−
b
a
a
λ
a
λ
c
λ
a
a
λ
a
c
λ
a
a
0
λ
>
0.
λ
<
λµ
+
a
λ
a
µ
a
λ
a
b
λ
a
λ
b
λ
µ
a
λ
a
µ
λ
a
a
0
a
a
a
0
a
0
a
a
0
a
a
0
a
a
a
0
a
a
a
0
a
a
a
a
a
0
a
a
a
AB
1
B
1
B
A
B
1
A
x
1
B
x
1
A
1
B
.l
5354.ru
14
между координатами проекций конца и начала вектора = на ось
называется проекцией этого вектора на ось
l
и обозначается пр
l
= пр
l
.
Итак,
. (2)
Под углом между вектором = и осью в пространстве понимается
угол между этим вектором и осью . Ось параллельна оси
l
, направлена,
как
l
, и проходит через точку – начало вектора. Этот угол всегда считается
положительным и измеряется в пределах Легко проверить, что
пр
l
=| | . (3)
Итак, проекция вектора на ось равна произведению его длины на косинус
угла между вектором и осью. Эта формула становится очевидной, если вектор
перенести параллельно самому себе так, чтобы его начало
A
лежало на оси
например, совпало с точкой
1
A
.
§ 5. Разложение вектора по базисным векторам
Возьмем в пространстве прямоугольную декартову систему координат
Oxyz. Здесь и в дальнейшем будем считать, что эта система правая, т. е. та-
кая, для которой поворот от оси
Ox
к оси
Oy
на угол, меньший
π
, совершает-
ся в направлении против хода часовой стрелки, если смотреть на плоскость
Oxy
из какой-либо точки положительной полуоси
.Oz
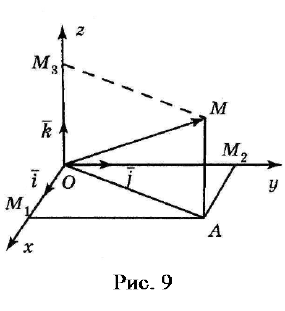
Пусть , , – единичные векторы, лежащие на
осях и направленные в положительную
сторону этих осей, а их начала совпадают с началом
координат O (рис. 9), | | = | | = | | = 1. Эти векторы
называются базисными (основными).
Пусть
a
– произвольный вектор в системе коор-
динат Перенесём его параллельно самому себе
так, чтобы начало вектора совпало с точкой О. По-
лучим вектор = . Пусть , и – проекции точки
M
на оси
и . Из рис. 9 видно, что
= = + + , = , = ⇒
= = + + (4)
1
B
x −
1
A
x
a
AB
l
a
AB
11
l
BA
пр a x x= −
ϕ
a
AB
l
'l
'l
A
0.
ϕπ
≤≤
a
a
cos
ϕ
a
,l
i
j
k
,Ox
,Oy
Oz
i
j
k
.Oxyz
a
OM
1
M
2
M
3
M
,Ox Oy
Oz
a
OM
1
OM
1
MA
AM
1
MA
2
OM
AM
3
OM
a
OM
1
OM
2
OM
3
OM
15
Пусть , , – проекции вектора = на оси и . Так как
– проекция на ось , то по формуле (2) имеем
1
0
;
xM
ax x= −
так как , то
1
.
xM
ax=
(5)
Пусть = , как показано на рис. 9. В этом случае
1
1M
x OM=
=| |.
По формуле (1) имеем =| | , но =| | и = , поэтому =
. Легко проверить, что эта формула остаётся справедливой при =
(при этом вектор будет направлен противоположно ). Аналогично бу-
дем иметь = , = . Подставим эти выражения в (4):
= + + . (6)
Получили формулу, которая называется разложением вектора по базисным
векторам. Коротко ее записывают в виде =( , , ), подчёркивая, что за-
дание вектора в пространстве равносильно заданию трёх чисел – проекций
этого вектора на оси координат. Числа , , называют также координа-
тами по отношению к базисным векторам , , . Слагаемые векторы
правой части (6) называют составляющими вектора
.a
Вектор с началом в точке О – начале координат – называется радиус-
вектором точки
,M
конца этого вектора. Покажем, что проекции на оси ко-
ординат радиус-вектора точки
M
равны координатам этой точки.
Пусть точка
M
имеет координаты в рассматриваемой системе
По определению абсциссы точки имеем , где – координата
точки
1
.M
Но согласно (5)
1
Mx
xa=
– проекции на ось т. е.
.
x
xa=
Анало-
гично
,
y
ya=
.
z
za=
Итак,
§ 6. Линейные операции над векторами,
заданными своими проекциями
Пусть векторы и заданы своими проекциями: =( , , ),
.
(,,)
xyz
b bbb=
Разложим векторы по формуле (6):
,
xy z
i a j ak
aa
++
=
.
xy z
i jkbb b b++=
Эти соот-
ношения почленно сложим и учтём, что по свойству умножения вектора на
число
()
x x xx
i bi a b i
a
+=+
. Получим
( )( ) ( )
xx yy zz
ababiabjabk+= + + + + +
или
+ =( + , + , + ). (7)
x
a
y
a
z
a
a
OM
,Ox Oy
Oz
x
a
a
Ox
0
0x =
x
a
1
0
M
x >
1
OM
1
OM
1
OM
i
1
M
x
1
OM
x
a
1
M
x
1
OM
x
a
i
x
a
1
0
M
x <
1
OM
i
2
OM
y
a
j
3
OM
z
a
k
a
x
a
i
y
a
j
z
a
k
a
x
a
y
a
z
a
x
a
y
a
z
a
a
i
j
k
OM
(,,)xyz
.Oxyz
M
1
M
xx=
1
M
x
a
,Ox
( ; ; ).OM x y z=
a
b
a
x
a
y
a
z
a
a
b
x
a
x
b
y
a
y
b
z
a
z
b
5354.ru
16
Аналогично для разности
– =( – , – , – ). (8)
Точно так же для произведения и
=( , , ). (9)
Формула (7) показывает, что проекция на ось координат суммы векторов
равна сумме проекций на эту ось слагаемых векторов. Подобное утверждение
имеет место для формулы (8). Формула (9) показывает, что при умножении
вектора на число на это число умножаются все проекции вектора.
§ 7. Длина вектора. Расстояние между двумя точками
Пусть вектор задан своими проекциями: =( , , ). Перенесём его
параллельно себе так, чтобы его начало совпало с началом координат. Полу-
чим = . Из рис. 9 видно, что
.
Согласно (5)
1
22 2
1
|| ,
Mx
OM x a= =
аналогично
и . Эти числа подставим в
предыдущую формулу и получим .
Извлечём квадратный корень и найдем длину век-
тора:
. (10)
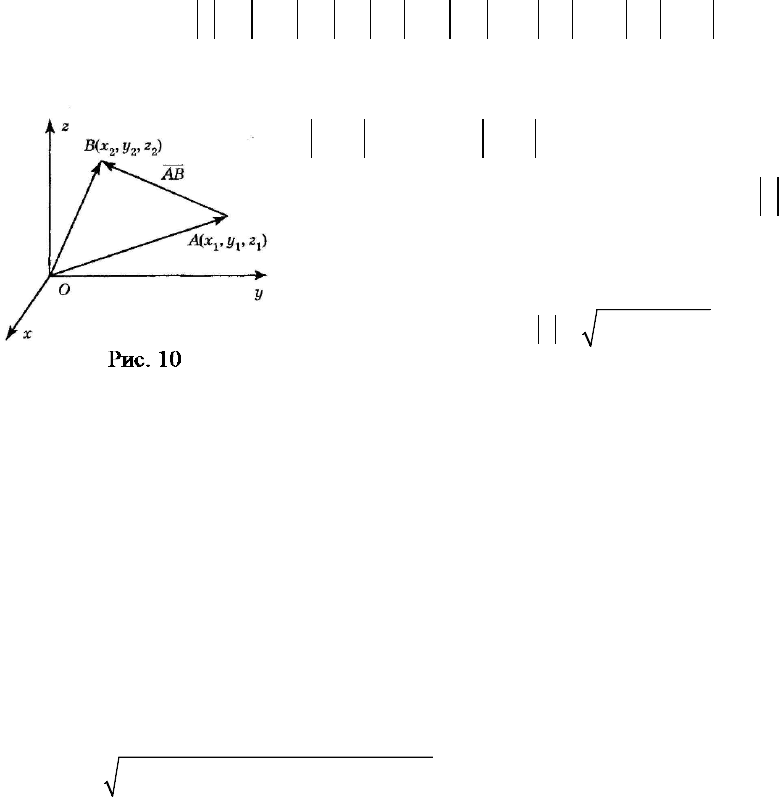
Задача. Пусть в пространстве Oxyz точки
A
и
B
заданы координатами А и В (рис. 10). Нужно найти расстоя-
ние между ними.
Так как координаты точки
A
равны проекциям на оси координат радиус-
вектора этой точки, то
1 11
(,,)OA x y z=
и = . Согласно (8) =
, но
.OB OA AB−=
Значит,
2 1 2 12 1
( ; ; ).AB x x y y z z=−−−
Отсюда
видно, что проекции на оси координат вектора равны разностям соответству-
ющих координат его конца и начала. Зная проекции , по формуле (10)
найдём длину вектора , следовательно, и расстояние между точками и
:B
| |=
a
b
x
a
x
b
y
a
y
b
z
a
z
b
λ
a
λ
a
λ
x
a
λ
y
a
λ
z
a
λ
a
a
x
a
y
a
z
a
a
OM
2 22 2 2 2 2
123
a OM OA AM OM OM OM==+= + +
2
2
2 y
OM a=
2
2
3 z
OM a=
2
222
xyz
a aaa=++
222
xyz
a aaa= ++
( )
1 11
;;xyz
( )
2 22
;;xyz
OB
( )
2 22
;;xyz
OB −
OA
( )
2 1 2 12 1
;;x xy yz z−−−
AB
AB
A
AB
( ) ( ) ( )
2 22
21 2 1 21
xx yy zz− +− +−

17
§ 8. Направляющие косинусы вектора
Пусть в пространстве Oxyz задан вектор =( , , ). Поместим его нача-
ло в начало координат. Пусть – углы, обра-
зованные вектором с осями координат Ox, Oy, Oz
(рис. 11). По формуле (3) для проекций этого векто-
ра на оси координат имеем
| |cos , | |cos , | |cos .
xyz
aa aa aa
αβγ
= = =
(11)
В правые части вместо | | подставим выражение
(10) и найдем косинусы углов:
222 222
cos ; cos ;
x xyz y xyz
a aaa a aaa
αβ
= ++ = ++
222
cos .
z xyz
a aaa
γ
= ++
(12)
Они называются направляющими косинусами вектора . Если все равенства
в (12) возведём в квадрат и почленно сложим, то получим
. Для единичного вектора, у которого | |=1, формулы
(11) примут вид . Отсюда
§ 9. Скалярное произведение векторов, угол между векторами.
Условие ортогональности двух векторов
Даны два вектора и , начала которых расположены в одной точке, а
угол между векторами равен . Такое расположение мы всегда можем полу-
чить, перенеся один из векторов параллельно.
Скалярное произведение двух векторов и обозначается (либо
) и определяется как число, равное произведению длин этих векторов на ко-
синус угла между ними, т. е.
( , )=| || | . (13)
Из определения ясно, что | | = (проекция на ). С учётом этого
соотношения формулу (13) запишем так:
( , ) = | |⋅ или ( , ) = | |⋅ . (14)
a
x
a
y
a
z
a
,,
αβγ
a
a
a
222
cos cos cos 1
αβγ
++=
0
a
cos ,
x
a
α
=
cos
y
a
β
= ,
cos
z
a
γ
=
0
a
( )
cos cos cos
αβγ
=;;
a
b
ϕ
a
b
(,)ab
a
b
a
b
a
b
cos
ϕ
b
cos
ϕ
a
пр b
b
a
a
b
a
a
пр b
a
b
b
b
пр a
5354.ru
18
Скалярное произведение двух векторов равно произведению длины одно-
го вектора и проекции другого вектора на направление первого. Угол
ϕ
меж-
ду векторами и
b
будем обозначать также
(,)ab
.
Скалярное произведение обладает следующими свойствами:
• ( , )=( , );
• ( , )=( , )= ( , ), где – скалярный множитель;
• ( , + )=( , )+( , ).
Первое свойство показывает, что сомножители можно поменять местами;
второе – что постоянный скалярный множитель можно вынести за знак ска-
лярного произведения; третье – что при скалярном умножении векторов мож-
но использовать правило умножения многочленов. Первые два свойства про-
веряются на основании определения скалярного произведения векторов, т. е. с
помощью формулы (13). Докажем третье свойство.
С учётом (14) запишем
( , + )=| |⋅ =| |⋅ +| |
a
пр c⋅
=( , )+( , ).
Пусть векторы заданы своими проекциями:
( , , ),
xyz
a aaa=
( , , ),
xyz
b bbb=
поэтому
= + + , = + + . Сначала для произведений базисных
векторов , докажем справедливость соотношений
( , )=1; ( , )=1; ( , )=1; (15)
( , )=0; ( , )=0; ( , )=0; (16)
Действительно, по формуле (13) имеем ( )=| || | , поэтому ( ,
)=1. Далее, ( , )=| || | =0. Остальные равенства в (15) и (16) дока-
зываются аналогично.
Запишем скалярное произведение
( , )=( + + , + + ).
Использовав второе и третье свойства скалярного произведения, будем иметь
( , )= ( , )+ ( , )+ ( , )+ ( , )+
+ ( , )+ ( , )+ ( , )+(
Отсюда с учётом (15) и (16) получим
a
a
b
b
a
λ
a
b
a
b
λ
λ
a
b
λ
a
b
c
a
b
a
c
a
b
c
a
( )
a
прbc+
a
a
пр b
a
a
b
a
c
a
x
a
i
y
a
j
z
a
k
b
x
b
i
y
b
j
z
b
k
,i
j
k
i
i
j
j
k
k
i
j
j
k
i
k
,i
i
i
i
( )
cos ,ii
i
i
i
j
i
j
( )
cos ,ij
a
b
x
a
i
y
a
j
z
a
k
x
b
i
y
b
j
z
b
k
a
b
x
a
x
b
i
i
x
a
y
b
i
j
x
a
z
b
i
k
y
a
x
b
j
i
y
a
y
b
j
j
y
a
z
b
j
k
z
a
x
b
k
i
(,) (,).
zy zz
ab k j ab kk+

19
( , )= + + . (17)
Таким образом, скалярное произведение векторов равно сумме произведе-
ний одноименных проекций этих векторов.
Вычисление угла между векторами. Запишем | | и | | через проекции с
использованием формулы (10). Из (13) следует, что . Следо-
вательно, согласно (17)
. (18)
Зная
cos ,
ϕ
найдем угол
Условие ортогональности (перпендикулярности) двух векторов. Если
для ненулевых векторов и их скалярное произведение ( , )=0, то вектор
ортогонален вектору
В самом деле, пусть ( , )=0, тогда согласно (13) имеем ( , )=| |⋅| |⋅
=0. Так как , , то =0. Значит, , т. е. векторы
ортогональны.
Условие ортогональности двух векторов с учётом (17) можно записать
следующим образом: + + =0.
§ 10. Векторное произведение векторов,
условие коллинеарности двух векторов, площадь треугольника
Даны два вектора и . Построим их, поместив начала в
общей точке и обозначая
ϕ
угол между ними (см. рис. 12).
Векторным произведением двух векторов и называется
вектор (обозначаемый
c ab= ×
), который обладает свойства-
ми:
• , т. е. длина вектора численно равна
площади параллелограмма, построенного на , как на сто-
ронах;
• , , т. е. перпендикулярен к плоскости указанного параллело-
грамма;
a
b
x
a
x
b
y
a
y
b
z
a
z
b
a
b
( )
cos , /( )a b ab
ϕ
=
222222
cos
xx yy zz
x y zx yz
ab ab ab
aaabbb
ϕ
++
=
++ ++
,0 .
ϕ ϕπ
≤≤
a
b
a
b
a
.b
a
b
a
b
a
b
( )
cos ,ab
0a ≠
0b ≠
( )
cos ,ab
, /2ab
π
=
x
a
x
b
y
a
y
b
z
a
z
b
a
b
a
b
sinc ab
ϕ
=
c
a
b
ca⊥
cb⊥
c
5354.ru
20
Рис. 13
• вектор направлен так, что если смотреть с его конца, то кратчайший
поворот от первого вектора ко второму вектору совершается против хода
часовой стрелки.
Для векторного произведения
ab×
применяют и другие обозначения:
, .
Векторное произведение обладает следующими свойствами:
( 1)[ ];ab ba×=− ×
[][][];ab a b ab
λ λλ
×=× = ×
() .a bc abac× + =×+×
Первые два свойства доказываются построением. Докажем справедли-
вость равенства
() .a bc abac× + =×+×
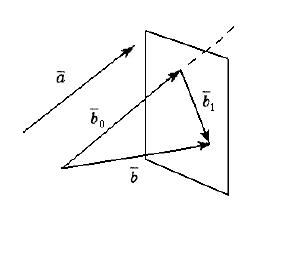
Вначале отметим, что любой вектор
b
можно пред-
ставить в виде
01
,bb b= +
где вектор
0
b
коллинеарен
,a
а
вектор
1
b
ортогонален
a
(см. рис. 13). Чтобы в этом убе-
диться, достаточно через начало вектора
b
провести
прямую, параллельную
,a
через конец вектора
b
прове-
сти плоскость, перпендикулярную
,a
точка их пересече-
ния служит концом
0
b
и началом
1
b
(начало
0
b
совпадает
с началом
b
, конец
1
b
– с концом
b
).
Замечая, что площадь параллелограмма, построенного на векторах
,
a
01
,
bb b
= +
равна площади параллелограмма, построенного на векторах
,
a
1
,
b
по-
скольку они имеют общую сторону
a
, одну и ту же высоту
1
b
, заключаем, что
01 1
() .bb bab a a×=× + =×
Аналогично для вектора
01
,
cc c
= +
где вектор
0
c
коллинеарен
,a
а вектор
1
c
ортогонален
,a
будем иметь
01 1
() .cc cac a a×=× + =×
Покажем, что
11 1 1
()a b c ab ac× + =× +×
или
12
,ddd= +
где
2
11 1 1 1
( ), ,d a b c d abd ac=×+ =× =×
суть векторы, лежащие в одной плоскости,
так как они перпендикулярны
.a
Здесь имеем
1 12 1
| | | || |, | | | || |,d ab d ac= =
c
a
b
ab
×
,ab
