Салимов Р.Б. Математика (для студентов бакалавриата)

Подождите немного. Документ загружается.

Доказательство. Пусть – заданное сколь угодно малое число. Нуж-

но доказать, что для этого числа найдётся такое число , что для всех

будет выполняться неравенство

.)()(

εϕ

<xfx

Это будет означать, что

рассматриваемое произведение есть бесконечно малая функция при .

Так как – ограниченная функция в интервале , то существует та-

кое число , что для всех точек интервала , т. е. для всех ,

имеет место неравенство

. (7)

Так как является бесконечно малой функцией при , то для числа

найдётся такое число , что для всех будет выполняться нера-

венство

. (8)

Пусть – наибольшее из чисел . Тогда для всех неравенства (7)

и (8) выполняются одновременно, поэтому с учётом свойства абсолютной ве-

личины произведения для всех имеем

() () () () .xfx x fx c

ϕϕ ε

= < ⋅=

Теорема доказана.

Следствия из теорем 2 – 5

Следствие 1. Функция, бесконечно малая при , является функци-

ей, ограниченной в некотором бесконечном интервале (согласно тео-

реме 2, поскольку указанная бесконечно малая функция имеет предел, равный

нулю, при ).

Следствие 2. Произведение двух бесконечно малых функций есть беско-

нечно малая функция (согласно теореме 5, так как любая из этих бесконечно

малых функций – функция ограниченная).

Следствие 3. Произведение постоянной на бесконечно малую функцию –

функция бесконечно малая (согласно теореме 5, т. к. постоянная есть ограни-

ченная функция).

0N >

xN>

x →+ ∞

()fx

( )

,N +∞

0c >

( )

,N +∞

xN>

()fx c≤

()x

x →+ ∞

0N >

xN>

() /xc

ϕε

xN>

x →+ ∞

( )

,N +∞

x →+ ∞

5354.ru

§ 8. Бесконечно большая функция,

ее связь с бесконечно малой

Функция называется бесконечно большой при , если для

любого числа , каким бы большим это число ни было, найдётся такое

число , что для всех будет выполняться неравенство .

Например, функция является бесконечно большой при . В са-

мом деле, здесь запишется как или, так как , в виде

, а для положительных в виде . Поэтому для всех имеет

место неравенство , каким бы большим число ни было. Ясно, что

– бесконечно большая функция при , и в качестве числа , указан-

ного в определении, можно взять .

Если – бесконечно большая функция при , то пишут

lim ( )

→∞

= ∞

и говорят, что функция стремится к бесконечности.

Если функция принимает только положительные значения, пишут

lim ( ) .

→∞

= +∞

Если функция принимает только отрицательные значения, то пишут

lim ( ) .

→∞

= −∞

В последних двух случаях говорят, что функция стремится к плюс

бесконечности, минус бесконечности соответственно, но знаки

не есть числа и над ними нельзя проводить операции, нельзя писать

или . Эти символы лишь обозначения бесконечно большой функции.

Покажем связь между бесконечно большой и бесконечно малой функ-

циями.

Теорема 6. Если – бесконечно большая функция при , то

– бесконечно малая функция при .

Доказательство. Пусть – заданное сколь угодно малое число. Дока-

жем, что для него найдётся такое число , что для всех будет вы-

полняться неравенство . Это и будет означать, что – беско-

нечно малая функция. Для указанного числа возьмём . Так как –

бесконечно большая функция при , то для числа найдётся такое

число , что для всех будет выполняться неравенство а

отсюда для всех имеем

()y fx=

x →+ ∞

0L >

0N >

xN>

()fx L>

yx=

x →+ ∞

()fx L>

xL>

x >0

xL>

0L >

x →+ ∞

()fx

x →+ ∞

()fx

,,∞+∞−∞

0∞−∞=

/1∞ ∞=

()fx

x →+ ∞

1/ ( )fx

x →+ ∞

0N >

xN>

1/ ( )fx

()fx

x →+ ∞

0N >

xN>

( ) 1/ ,fx

xN>

. (9)

Согласно свойству абсолютной величины дроби . Теперь не-

равенство (9) для всех можно записать так: . Теорема доказа-

на.

Теорема 7 (обратная предыдущей). Если – бесконечно малая функ-

ция при , не обращающаяся в нуль, то – бесконечно большая

функция при .

Доказательство аналогично предыдущему.

Теоремы 6 и 7 условно записывают так: и . Отметим, что

при других способах изменения определение бесконечно большой функции

даётся аналогично, например, функция называется бесконечно большой

при , если

00 0

0 0 ( ), | ( ) | .L x x x x x fx L

δ δδ

∀> ∃> ∀ − < < + ≠ ⇒ >

§ 9. Свойства пределов

Теорема 8. Если – функция, имеющая при предел, равный

числу , то эту функцию можно представить в виде суммы числа и неко-

торой бесконечно малой функции при , т. е. .

Доказательство. Пусть – заданное сколь угодно малое число. Обо-

значим

(10)

и покажем, что – бесконечно малая функция. Так как имеет предел

равный , то согласно определению предела для указанного числа

найдётся такое число , что для всех будет выполняться неравен-

ство или с учётом введённого выше обозначения .

Итак, для всех имеем . Это означает, что – бесконечно

малая функция, и мы получаем из (10) . Теорема доказана.

Теорема 9 (обратная теореме 8). Если функцию можно предста-

вить в виде суммы числа и некоторой бесконечно малой функции при

, то число есть предел функции при .

Теорема доказывается аналогично теореме 8.

1/ ( )fx

1/ ( ) 1/ ( )fx fx=

xN>

1/ ( )fx

()x

x →+ ∞

1/ ( )x

x →+ ∞

1/ 0∞=

1/0= ∞

()fx

xx→

()fx

x →+ ∞

()xα

x →+ ∞

() ()fx b x= +α

() ()fx b x−=α

()x

()fx

0N >

xN>

( )

fx b

−<

()x

αε

xN>

()x

αε

()x

() ()fx b x

= +

()fx

()x

x →+ ∞

()fx

x →+ ∞

5354.ru

Теорема 10. Предел алгебраической суммы конечного числа функций ра-

вен алгебраической сумме пределов слагаемых функций, если последние пре-

делы существуют.

Например, для двух функций

Теорема 11. Предел произведения конечного числа функций равен произ-

ведению пределов этих функций, если последние пределы существуют.

Например, для двух функций

. (11)

Теорема 12. Предел дроби (частного) равен отношению предела числи-

теля к пределу знаменателя, если оба последних предела существуют и пре-

дел знаменателя не равен нулю.

Эти три теоремы доказываются аналогичным образом. Докажем теорему

11. Нам дано, что

, (12)

( – некоторые числа). Тогда по теореме 8 , где

, – бесконечно малые функции при . Запишем произведение

()() [ () ()f x x bc b x c x

ϕ βα

=+ ++

( ) ( )].xx

αβ

Слагаемые в правой части в квадрат-

ных скобках -бесконечно малые функции, согласно следствиям из теорем 2 –

5. Тогда сумма в этих скобках, согласно теореме 4, тоже бесконечно малая

функция, поэтому число , согласно теореме 9, есть предел функции

. Итак, . Подставив в правую часть вместо и

пределы (12), придем к формуле (11). Теорема доказана.

Следствие из теоремы 11. Постоянный множитель можно выносить за

знак предела: , .

В самом деле, если , то (поскольку предел

постоянной равен этой же постоянной, что ясно из определения предела). По

формуле (11) получим

[ ]

lim () () lim () lim ()

x xx

fx x fx x

ϕϕ

→+∞ →+∞ →+∞

+= +

[ ]

lim () () lim () lim ()

x xx

fx x fx x

ϕϕ

→+∞ →+∞ →+∞

⋅= ⋅

lim ( )

fx b

→+∞

lim ( )

→+∞

,bc

() (),fx b x

= +

() ()xc x

ϕβ

= +

()x

x →+ ∞

() ()fx x

⋅

[ ]

lim () ()

fx x bc

→+∞

⋅=⋅

[ ]

lim ( ) lim ( )

Ax A x

ϕϕ

→+∞ →+∞

constA −

()fx A=

lim ( ) lim

fx A A

→+∞ →+∞

= =

[ ]

lim () () lim () lim () lim ()

x xx x

fx x fx x A x

ϕ ϕϕ

→+∞ →+∞ →+∞ →+∞

⋅= ⋅ =⋅

§ 10. Переход к пределу в неравенствах

Теорема 13. Пусть для всех и функции и при

имеют один и тот же предел, равный . Тогда тот же предел

при имеет функция , заключённая между и .

Доказательство. Пусть – заданное сколь угодно малое число. Так

как при имеет предел, равный , то для числа найдётся

число , такое, что для всех будет выполняться неравенство

. Аналогично, так как имеет при предел, равный , то

для указанного числа найдётся такое число , что для всех будет

выполняться неравенство . Пусть – наибольшее из чисел и

. Тогда для всех выполняются оба предыдущих неравенства. Значит,

для всех имеют место следующие неравенства, равносильные соответ-

ствующим предыдущим: Поэтому для всех

с учетом условия теоремы будем иметь

Отсюда для всех ,

т. е. справедливо неравенство , равносильное последнему.

Итак, для всех имеем , но это означает, что есть предел

при . Теорема доказана.

Легко проверить, что теорема остаётся справедливой и в том случае, ко-

гда для всех .

Теорема 14. Если для всех функция и существует предел этой

функции при , то этот предел неотрицателен:

lim ( ) 0.

→∞

≥

Доказательство. Дано, что существует предел , который мы

обозначим . Нужно доказать, что .

Предположим обратное, т. е. что (хотя все условия теоремы выпол-

няются). Выберем число настолько малым, чтобы было . Так как

функция имеет при предел, равный , то для выбранного числа

найдётся такое число , что для всех будет выполняться нера-

венство или равносильное ему неравенство По-

этому для всех получим . Итак, для всех будем иметь

. Но это противоречит условию теоремы, следовательно, предположе-

ние, что , должно быть отброшено. Теорема доказана.

() () ()x fx gx

()gx

()x

x →+ ∞

()fx

()gx

()x

x →+ ∞

( )

ϕε

−<

()gx

x →+ ∞

( )

gx b

−<

xN>

( )

,b xb

εϕ ε

−< <+

( )

.b gx b

εε

−< <+

xN>

( ) ( )

(), () .b x fx fx gx b

εϕ ε

−< < < <+

()b fx b

εε

−< <+

xN>

( )

fx b

−<

xN>

( )

fx b

−<

()fx

x → +∞

)))x f x gxϕ(≤(≤(

() 0fx>

x → +∞

lim ( )

→+∞

0b ≥

0b <

0b +ε<

()fx

x → +∞

0N >

xN>

( )

fx b

−<

() .b fx b

εε

−< <+

xN>

() 0fx b

<+<

xN>

( )

0fx<

0b <

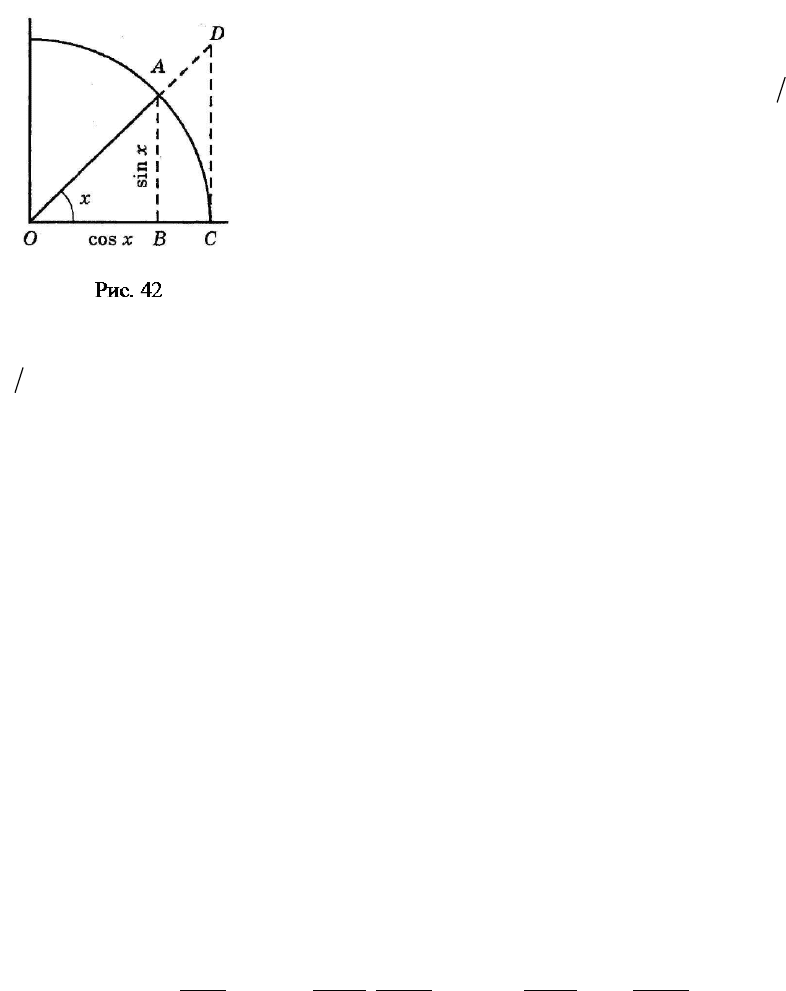
5354.ru

Легко проверить, что теорема остаётся справедливой, когда для

всех .

§ 11. Первый замечательный предел

Докажем равенство . Возьмем круг единичного радиуса.

Пусть есть угол между векторами и , измеренный в радианах (см.

рис. 42). Будем считать угол положительным, если он отсчитывается про-

тив хода часовой стрелки от вектора , и отрица-

тельным, если отсчёт ведётся в противоположном

направлении. Будем считать пока . Из рис. 42

видно, что , , , а также что

и при . Это верно и при

. Площади треугольников и кругового сектора,

указанных на рис. 42, связаны соотношением

OCDсектораOCAOBA

SSS

∆∆

которое принимает вид

или (после умножения на положительное число

) . В последнем неравенстве перейдём к обратным

величинам, при этом знаки неравенства изменятся на обратные:

. (13)

Последнее неравенство получено для . Пусть теперь . Тогда и

справедлива формула (13), т. е. . Учитывая,

что и , опять придём к неравенству (13), но уже для

Итак, неравенство (13) справедливо как для , так и для . Перей-

дем в нем при к пределу (к обычному пределу, когда , принимая

как положительные, так и отрицательные значения). Однако крайние части

(13) имеют один и тот же предел, равный 1. Поэтому по теореме 13 получим

предел , который называют «первым замечательным преде-

лом».

Пример.

00 0 0

(3 0) (3 0)

tg3 sin3 1 sin3 1

3 3 3 1 1 3.

3 cos3 3 cos3

lim lim lim lim

xx x x

xx x

x xx x x

→→ → →

→→



= ⋅ ⋅ = ⋅ = ⋅⋅=





() 0fx≥

lim (sin / ) 1

→



  



02x

cosOB x=

sinBA x=

tgCD x=

cos 1OB x= →

sin 0BA x= →

0x →

0x <

(sin cos )/2 /2 tg )/2xx x x< <(

2 sin x

cos /sin cosxx x x< < 1/

1/cos sin )/ cosx xx x>( >

0x >

0x <

0x−>

1/cos( )x−<

sin())/()cos()xx x<( − − < −

sin( ) sinxx−=−

cos( ) cosxx−=

0x <

0x >

0x <

0x →

lim (sin / ) 1

→

§ 12. Предел последовательности.

Второй замечательный предел. Натуральные логарифмы

Дана функция , где принимает целые положительные значения.

Она называется функцией натурального аргумента и принимает значения

, ,…, ,… Последние образуют последовательность

чисел Эту последовательность коротко записывают . Таким

образом, задание функции натурального аргумента равносильно заданию по-

следовательности. По аналогии с определением предела функции при

дадим определение предела функции натурального аргумента (после-

довательности).

Число называется пределом функции натурального аргумента

при или последовательности , если для любого числа

каким

бы малым оно ни было, найдётся такое натуральное число

что для всех

будет выполняться неравенство или . В этом

случае пишут или .

Функция натурального аргумента (последовательность )

называется возрастающей, если или убывающей,

если Рассматриваемая функция (последователь-

ность) будет ограниченной, если существует такое положительное число

что для всех выполняется неравенство . Например, функция

или последовательность являются убывающими. В самом

деле, каждое последующее значение меньше предыдущего, т. е.

Кроме того, последовательность является ограниченной, т. к. для всех вы-

полняется неравенство .

Без доказательства запишем несколько теорем.

Теорема 15. Всякая возрастающая ограниченная последовательность

(функция натурального аргумента) имеет конечный предел.

Эта теорема утверждает только лишь существование предела, но не ука-

зывает, как его найти.

Теорема 16. Функция натурального аргумента имеет при

предел, заключённый между числами 2 и 3.

()

y fn=

(1)yf=

(2)yf=

()

y fn=

, ,..., ,...

yy y

{ }

()fx

x →∞

()

y fn=

n →∞

{ }

nN>

( )

fn b

−<

lim ( )

fn b

→∞

lim

→∞

()

y fn=

{ }

123

yyy< < < ...

1nn

< < < ...

123 1nn

yyy yy

> > > ... > > > ...

yc≤

( ) 1/

y fn n= =

{ }

1/n

1>1/2 >1/3 > ...

1/ 1n ≤

(1 1 )

yn= +

n →∞

5354.ru

При доказательстве этой теоремы сначала устанавливают, что эта функ-

ция является возрастающей и ограниченной. Поэтому согласно теореме 15

предел функции существует. Его обозначают через и пишут

lim 1 .

→∞







Можно показать (принимается без доказательства), что число является ир-

рациональным. Его приближённое значение

2.718282.e ≅

Теорема 17. Функция

(1 1/ )

= +

при имеет предел, равный :

lim 1

→∞







. (14)

Предел (14) называют «вторым замечательным пределом».

Пример.

22 3

4 13 3

11 1

lim lim lim

xx x



+ + +⋅





→∞ →∞ →∞

+ ++



= = +



++ +



Пусть

,( 1) / 3xy+=

при этом

,y →∞

когда

.x →∞

Тогда последний предел примет

вид

11 1 1

1 1 1 1 1.

lim lim lim

y yy

yy y y

→∞ →∞ →∞

  

  

+ + = + ⋅ + = ⋅=

  

  

  

  

  

Логарифм называется натуральным, если его основание равно ,

т. е. . Этот логарифм обозначают .

Пусть . Тогда по определению логарифма . От последнего со-

отношения возьмём десятичный логарифм и получим . По свойству

логарифма будем иметь . Но , следовательно,

. (15)

В этой формуле – известное число (т. к. – число известное, то и его

десятичный логарифм известен: ), поэтому формула (15) выражает

десятичный логарифм через его натуральный логарифм. Ясно, что и,

наоборот, по можно найти .

x →∞

log

ae=

ln x

lnyx=

ex=

lg lg

ex=

lg lgye x=

lnyx=

(ln )lg lgxe x=

lge

lg 0.4343e ≅

lg x

ln (lg )/(lg )x xe=

§ 13. Сравнение бесконечно малых функций

Пусть , – бесконечно малые функции при , т. е.

и . Бесконечно малая функция называется бес-

конечно малой функцией одного порядка с бесконечно малой функцией ,

если существует конечный предел .

Бесконечно малая функция называется бесконечно малой функцией

более высокого порядка, чем , если существует конечный предел

. Значит, проще говоря, стремится к нулю быстрее, чем

Бесконечно малая функция называется бесконечно малой функцией

более низкого порядка, чем , если , т. е., упрощенно,

стремится к нулю медленнее, чем .

Если не существует конечный или бесконечный предел ,

то говорят, что бесконечно малые функции и не сравнимы по отно-

шению.

Бесконечно малая функция называется бесконечно малой функцией

порядка ( – определённое число) по отношению к бесконечно малой

функции , если существует конечный предел

Например, функция есть бесконечно малая функция второго

порядка по отношению к бесконечно малой функции при .

В самом деле, здесь имеем

Отметим, что две бесконечно малые функции и одного и того

же порядка называются эквивалентными при , если

Пример. При

x →∞

бесконечно малые

()

()x

– эквивалент-

ные бесконечно малые, так как предел их отношения равен единице. Дей-

ствительно,

()x

x → +∞

lim ( ) 0

→+∞

lim ( ) 0

→+∞

()x

lim [ ( )/ ( )] 0

ϕψ

→+∞

≠

()x

lim [ ( )/ ( )] 0

ϕψ

→+∞

()x

lim [ ( )/ ( )]

ϕψ

→+∞

= ∞

()x

lim [ ( )/ ( )]

ϕψ

→+∞

()x

()

lim 0

[ ( )]

→+∞

≠

() 1xx

x → +∞

[ ] [ ]

() 1

lim lim lim 1 1

() 1

x xx

→+∞ →+∞ →+∞

= = =

()x

x → +∞

lim [ ( )/ ( )] 1

ϕψ

→+∞

5354.ru

Рис. 43

22 2

lim lim lim lim 1 1.

()

( ) ( 3)/

xx x x

x xx

→∞ →∞ →∞ →∞



= = +=





§ 14. Непрерывность функции в точке и на интервале

Функция называется непрерывной в точке , если

. (16)

Это означает, что:

• существует , т. е. функция определена в точке

xc=

и всюду

вблизи точки

xc=

;

• существует предел (существуют равные друг другу односто-

ронние пределы );

• ( ).

Как видно из (16), предел непрерывной функции можно вычислить под-

становкой в функцию предельного значения ее аргумента. Кроме того,

можно записать так: . Этот предел подставим в правую часть

формулы (16) и получим . Это равенство показывает, что

знак предела и знак непрерывной функции можно переставить.

Если функция непрерывна в каждой точке открытого интервала

или замкнутого интервала , то её называют непрерывной в соот-

ветствующем интервале.

Ясно, что для замкнутого интервала соотношение (16) считаем выполнен-

ным во всех точках этого интервала, включая концы, т. е. в частности

и . Здесь предел в точке представляет собой

предел справа, так как слева от этой точки

функция не определена. Аналогично в точке

имеем предел слева, так как справа от точки

функция не определена.

Геометрический смысл непрерывности

функции заклю-чается в том, что её график

представляет собой сплошную, без разрывов,

линию. В самом деле, изобразим на плоскости

график непрерывной функции

()y fx=

xc=

lim ( ) ( )

fx fc

→

()fc

()fx

lim ( )

→

lim ( ) lim ( )

xc xc

fx fx

→− →+

lim ( ) ( )

fx fc

→

lim ( ) lim ( ) ( )

xc xc

fx fx fc

→− →+

= =

xc=

xc→

lim

→

lim ( ) (lim )

xc xc

fx f x

→→

()fx

(, )ab

,ab





lim ( ) ( )

fx fa

→

lim ( ) ( )

fx fb

→

Oxy

()y fx=