Салимов Р.Б. Математика (для студентов бакалавриата)

Подождите немного. Документ загружается.

141

ГЛАВА 8. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ

ПРОИЗВОДНЫХ

§ 1. Производная длины дуги кривой

Пусть в плоскости

Oxy

задана кривая

( )

y fx=

(рис. 76), точка

с абс-

циссой

– фиксированная точка кривой, а точка

с абсциссой

– пере-

менная точка. Введём понятие длины дуги части

заданной кривой. Дугу



разделим на

частей точками

12 1

, ,..., .

MM M

−

 

Каждые две соседние точ-

ки, включая

соединим хордой и получим

ломаную

012

...MMM M



, соеди-няющую точки

и состоящую из

звеньев. Длину ломаной

обозначим через

Число

всех звеньев устре-

мим к бесконечности так, чтобы длины звеньев

стремились к нулю. При этом вышеуказанная

ломаная по форме будет приближаться к дуге



.MM

Поэтому за длину дуги кривой

есте-

ственно принять

lim .

→∞

Так как

– переменная точка с абсциссой

то с

изменением положения точки

(с изменением абсциссы

этой точки) дли-

на дуги

изменяется. Следовательно, эта дуга есть функция от

– абсциссы

точки

Обозначим ее

( )

.s sx=

На кривой возьмём точку

с абсциссой

.xx+∆

На рис. 76 показан слу-

чай, когда

0.x∆>

Длина дуги кривой



получается из функции

( )

заме-

ной

на

,xx+∆

т. е. заменой абсциссы

точки

на абсциссу

xx+∆

точки

Итак, длина дуги кривой



есть

( )

.sx x+∆

Длина дуги



( ) ( )

MM sx x sx s= +∆ − =∆

– это приращение функции

( )

в точке

соответ-

ствующее приращению

.x∆

Поэтому

( )

lim .

∆→

∆

′

∆

(1)

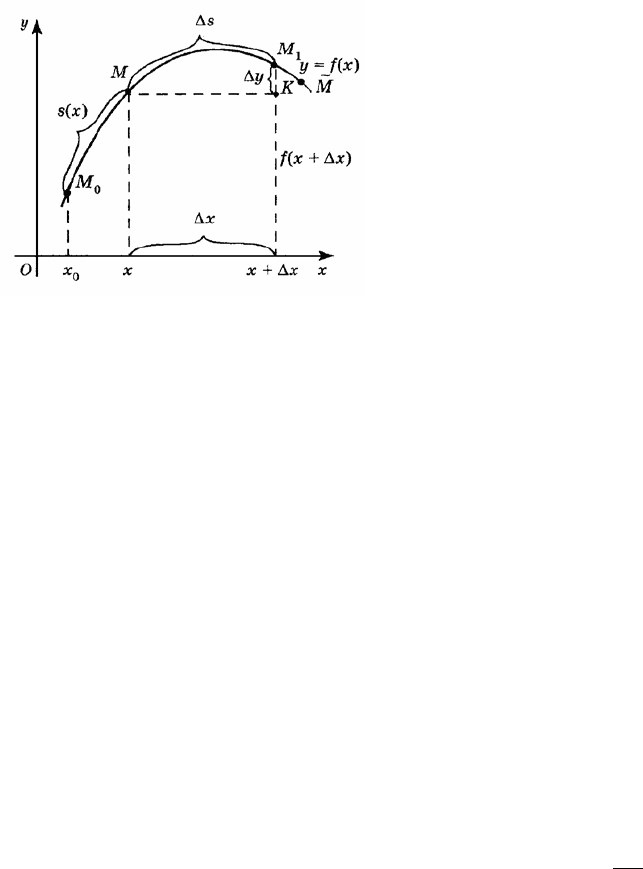
Рис. 76

5354.ru

142

Точка

с абсциссой

кривой

( )

y fx=

имеет ординату

( )

,fx

а ордината

точки

равняется

( )

.fx x+∆

Тогда разность этих ординат есть

( ) ( )

fx x fx y+∆ − =∆

– приращение функции, соответствующее приращению

x∆

и вычисляемое для точки

, причем

lim( / ) .

yx y

∆→

′

∆∆=

Из треугольника

MKM

, у которого сторона

,KM y= ∆

получаем

( ) ( ) ( )

222

.MM x y=∆ +∆

Это от-

ношение разделим на

( )

x∆

и получим

( ) ( ) ( ) ( )

22 22

/ 1 /.MM x y x∆ = +∆ ∆

Отсюда

( )

∆



= +



∆∆



∆

(2)

Будем считать, что кривая с уравнением

( )

y fx=

такова, что функция

( )

y fx=

имеет непрерывную производную

( )

.fx

′

Можно показать, что для такой кри-

вой (принимается без доказательства) имеет место условие

lim 1.

∆→

→

∆

(3)

Иначе говоря, предел отношения длины хорды

, стягивающей дугу с

длиной

s∆

, к длине

s∆

этой дуги равен 1. В соотношении (2) перейдём к пре-

делу, когда

MM→

0.x∆→

Учтём, что слева предел произведения равен

произведению пределов. Справа предел суммы равен сумме пределов и пре-

дел квадрата (произведения) равен квадрату (произведению) пределов. В ито-

ге имеем

lim lim 1 lim .

MM x x

sx x

→ ∆→ ∆→

∆∆



  

= +

  



∆∆ ∆

  



Слева первый предел согласно (3) равен 1, а второй предел равен

( )

′

со-

гласно (1). Справа предел равен

( )

.yx

′

Значит,

( )

1,sx yx

′′

= +

т. е.

( ) ( )

sx y

′′

= +

(4)

Получили формулу для вычисления производной длины дуги кривой

( )

,s sx=

когда эта кривая задана уравнением

( )

.y fx=

§ 2. Кривизна кривой на плоскости

Пусть на плоскости

Oxy

задана кривая. Возьмем на ней дугу



и в точ-

ках

проведём касательные к кривой (рис. 77). Угол

на который по-

143

ворачивается касательная к кривой в точке

когда точка

стремится к

точке

, называется углом смежности дуги



.MM

Отношение угла смежно-

сти

к длине дуги



(5)

характеризует искривленность дуги



данной дли-

ны.

В самом деле, чем больше дуга



искривлена,

тем больше угол смежности

и тем больше отношение (5). Например, для

дуги





той же длины, что и дуга



,MM

угол смежности



αα

так как дуга





искривлена больше, чем исходная дуга, и







/ /.M M MM

αα

Но нас инте-

ресует искривлённость не всей дуги



,MM

а искривлённость кривой в точке

Ясно, что чем ближе точка

к точке

тем лучше отношение (5) ха-

рактеризует искривлённость кривой в точке

Ясно также, что искривлён-

ность кривой в точке

наиболее полно характеризует предел отношения (5),

когда

.MM→

Этот предел называют кривизной кривой в точке

и обозна-

чают

Итак,



lim [ / ].

K MM

→

(6)

Легко показать, что кривизна окружности радиуса

в любой её точке равна

числу

1.R

Теперь получим формулу для вычисления кривизны кривой.

Пусть на плоскости

Oxy

задана кривая

( )

y fx=

(рис. 78) и функция

(

)

имеет вторую

производную. В точке

этой кривой с абсцис-

сой

требуется вычислить кривизну

этой кри-

вой. Пусть на рассматриваемой кривой

–

фиксированная точка, а

– переменная точка с

абсциссой

Длину дуги



обозначим

( )

.sx

На кривой возьмём точку

с абсциссой

.xx+∆

Длина дуги



( )

.MM sx x= +∆

Поэтому длина дуги



( ) ( )

,MM sx x sx s= +∆ − =∆

где

s∆

– приращение функции

( )

в точке

, соответствующее приращению

.x∆

Поэтому

lim( / ) .

sxs

∆→

′

∆∆=

Известно, что вычисленная в точке

производная

()

y fx

′

равна тангенсу

5354.ru

144

угла

образованного с осью абсцисс касательной к кривой в её точке

абсциссой

Ясно, что этот угол

будет изменяться с изменением абсциссы

точки

Это значит, что

есть функция от

, которую обозначим

( )

точке кривой

с абсциссой

xx+∆

этот угол будет равен

( )

.xx

+∆

Ясно, что

разность

( ) ( )

xx x

ϕ ϕϕ

+∆ − =∆

– приращение функции

( )

в точке

соответ-

ствующее приращению

.x∆

Поэтому

lim[ / ] .

ϕϕ

∆→

′

∆ ∆=

(7)

Из треугольника

123

NNN

(см. рис. 78), образованного вышеука-занными каса-

тельными и осью

, видно, что

( ) ( )

xx x

ϕ ϕϕ

+∆ − =∆

– угол между касатель-

ными, следовательно,

∆

есть угол смежности дуги



,MM

длина которой рав-

на

.s∆

Поэтому согласно формуле (6) (в которой

нужно заменить на

∆

)

для

– кривизны кривой в точке

– имеем



lim [ / ] lim[ / ].

MM x

K MM s

ϕϕ

→ ∆→

∆→

= ∆ = ∆∆

правой части и числитель, и знаменатель поделим на

,x∆

получим

lim .

∆→

∆∆

Предел отношения равен отношению пределов, поэтому

(lim )/ lim .

K x sx

∆→ ∆→

= ∆ ∆ ∆∆

Согласно (7) предел числителя равен

′

а предел знаменателя равен

′

Сле-

довательно,

′′

. (8)

Но

tg ,

′

следовательно,

arctg .

′

Возьмём отсюда производную по

при этом учтём, что правая часть – сложная функция от

Имеем

( )

′′

′

′′

= =

′′

Это выражение подставим в числитель (8), а в знаменатель запишем выраже-

ние (4) вместо

′

Тогда

( )

′′

′

(9)

Эта формула позволяет вычислить кривизну кривой в её точке

с абсциссой

когда кривая задана уравнением

( )

.y fx=

Сказанное относится к любой

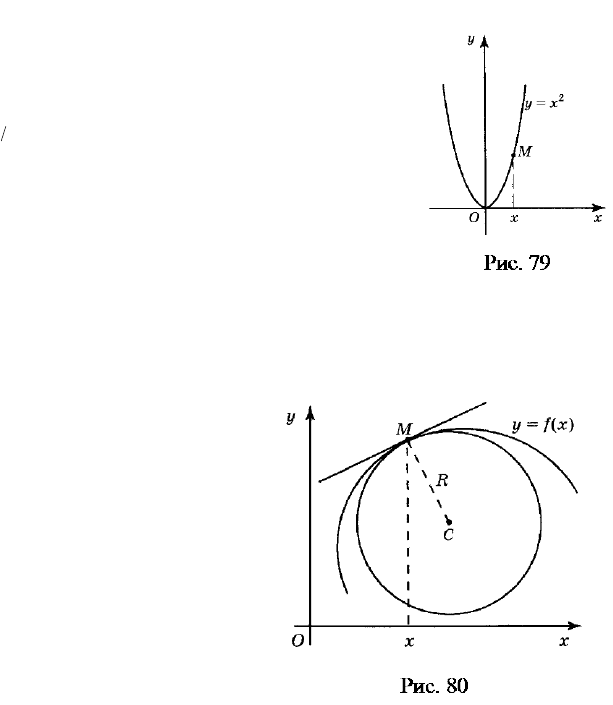
145

точке

т. е. в каждой точке кривой будет своя кривизна

– функция от

– абсциссы точки

Иногда кривизну

считают величиной положительной

и в формуле (9) берут абсолютную величину правой части,

принимая, что в исходной формуле (6) угол смежности

бе-

рётся без знака. Например, пусть

, 2 , 2.

x xx

yx y xy

′ ′′

= = =

Фор-

мула (9) даёт

( )

21 2 .Kx

−

= +

Эта формула определяет кри-

визну параболы с уравнением

yx=

(рис. 79) в любой её точке

с абсциссой

Например, в начале координат (0.0) кривиз-

на

2.K =

§ 3. Радиус, центр и круг кривизны кривой на плоскости

Пусть в плоскости

Oxy

задана кривая с урав-

нением

( )

,y fx=

причем функция

(

)

имеет вто-

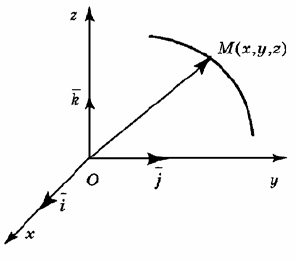
рую производную (рис. 80). Для этой кривой по

формуле (9) найдем кривизну в точке

с абсцис-

сой

Будем считать, что

0.K >

Радиусом кривизны этой кривой в точке

называется число, обозначаемое

и равное

1/ ,RK=

где

– только что найденная кривизна.

В точке

проведём нормаль (прямую, перпендикулярную к касатель-

ной) в сторону вогнутости кривой. На этой нормали отложим отрезок

.MC R=

Точка

называется центром кривизны кривой

( )

y fx=

для её точки

Круг

радиуса

с центром в точке

называется кругом кривизны этой кривой для

точки

Ясно, что для каждой точки

будут свои радиус, центр и круг

кривизны, т. е. с изменением положения точки

они изменяются.

5354.ru

146

§ 4. Параметрические и векторное уравнения линии в про-

странстве

Пусть в пространстве

Oxyz

задана точка

( )

;;M xyz

(рис. 81), а ее координаты представляют

собой заданные функции некоторого аргумента

–

параметра, т. е.

( ) ( ) ( )

, ,.x xt y yt z zt= = =

(10)

С изменением

значения этих функций изменяют-

ся, следовательно, изменяются координаты

точки

, и эта точка описывает некоторую линию в пространстве. Соотно-

шения (10) называются параметрическими уравнениями этой линии. Каждое

из уравнений (10) умножим соответственно на базисные векторы

,,i jk

 

сложим. Получим

( ) ( ) ( )

.xiyjzkxtiytjztk++= + +

   

(11)

Левую и правую части этого соотношения обозначим

.r xi y j zk=++



(12)

( ) ( ) ( ) ( )

.rt xti yt j ztk=++

 

(13)

Тогда соотношение (11) запишется так:

( )

.r rt=



(14)

Формула (14) называется векторным уравнением рассматриваемой кривой.

Как видно из (12) и (13), выражение (14) есть радиус-вектор точки

начало которого всегда совпадает с началом координат, а его конец – точка

– описывает вышеуказанную линию.

Пример (винтовая линия). Пусть в системе координат

Oxyz

задан круго-

вой цилиндр с образующими, параллельными

.Oz

Его направляющей служит

расположенная на плоскости

Oxy

окружность радиуса

с центром в начале

координат

( )

0; 0; 0 .

Пусть

( )

;;M xyz

– произвольная точка цилиндра. Через неё

проведём образующую, пересекающую плоскость

Oxy

в точке

Пусть

есть

угол, образованный радиусом

с осью

.Ox

Этот угол отсчитывается от

считается положительным, когда отсчёт ведётся против хода часовой стрелки,

Рис. 81

147

если смотреть навстречу оси

,Oz

и этот угол считается отрицательным, если

он отсчитывается в противоположном направлении.

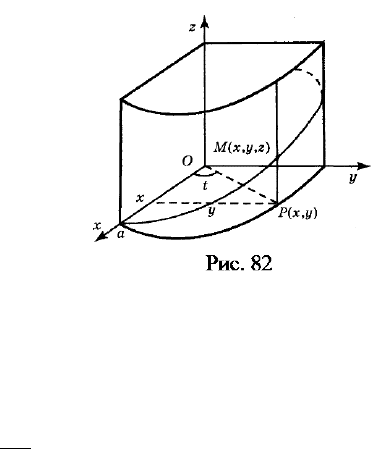
Как видно из рис. 82, координаты точки

определяются формулами

cos , sin .xa ty a t= =

Такими же будут абсцисса и ордината точки

Пусть ап-

пликата

точки

выражается формулой

/(2 ),z ht

где

– заданное поло-

жительное число.

Итак, координаты точки

определяются формулами

cos , sin , /(2 ).x a t y a t z ht

= = =

(15)

Ясно, что положение точки

зависит от значения

При

0t =

точка

сов-

падает с точкой

и находится на оси

.Ox

С увеличением

точка

движется

по окружности, а точка

находясь с ней на одной

образующей, движется по цилиндрической поверх-

ности, поднимаясь вверх. При

точка

ока-

жется на плоскости

Oxz

на высоте

.zh=

Эта линия

называется винтовой. При неограниченном увели-

чении

точка

поднимается вверх, а когда

при-

нимает отрицательные значения и стремится к

,−∞

точка

винтовой линии уходит неограниченно вниз.

Ясно, что (15) представляют собой параметрические уравнения этой винтовой

линии. Поступая, как ранее, запишем векторное уравнение винтовой линии в

виде (14), где

( )

cos sin .

r t a ti a t j tk

=++

  

§ 5. Предел и производная векторной функции

скалярного аргумента

Введённое выше выражение

( ) ( ) ( ) ( )

rt xti yt j ztk=++

 

(16)

называется векторной функцией скалярного аргумента

Пределом функции

(16) при

,tt→

где

– заданное число, называется вектор, определяемый

формулой

( ) ( ) ( ) ( )

00 0 0

lim lim lim lim .

tt tt tt tt

rt xti yt j ztk

→→ → →

=++

 

(17)

5354.ru

148

И в дальнейшем пределы берутся при

,tt→

но это условие для простоты за-

писи будем опускать. Длина вектора в формуле (17) равна

( ) ( )

(

)

( )

(

)

( )

(

)

2 22

lim lim lim lim .rt xt yt zt= ++



Но квадрат предела равен пределу

квадрата, и под корнем мы получим сумму пределов квадратов, которая равна

пределу суммы. Поэтому имеем

( ) ( )

( )

222

lim lim .rt xt yt zt



= ++





В свою очередь, знаки корня и предела можно переставить, так как квадрат-

ный корень – непрерывная функция своего аргумента. В правой части после

перестановки знаков корня и предела под знаком предела получим

( )

222

,xt yt zt++

а это есть ни что иное, как длина вектора

( )



форму-

лы (16), т. е.

( )

.rt



Итак, имеем

( )

lim lim .rt rt=



(18)

Начало векторной функции

( )



всегда будем помещать в начале координат

.Oxyz

Тогда при изменении

эта векторная функция изменяется по длине и

направлению, и конец этой векторной функции (точка

) в системе коорди-

нат

Oxyz

описывает некоторую линию. Каждому значению параметра

отве-

чает определённый вектор

( )



с концом

координаты которой равны про-

екциям вектора

( )



на оси координат, т. е.

( ) ( ) ( )

,,x xt y yt z zt= = =

. (19)

Наряду с указанным выше значением параметра

возьмём новое его значение

.tt+∆

Этому значе-

нию на кривой отвечает точка

радиус-вектор

которой есть

( )

rt t+∆



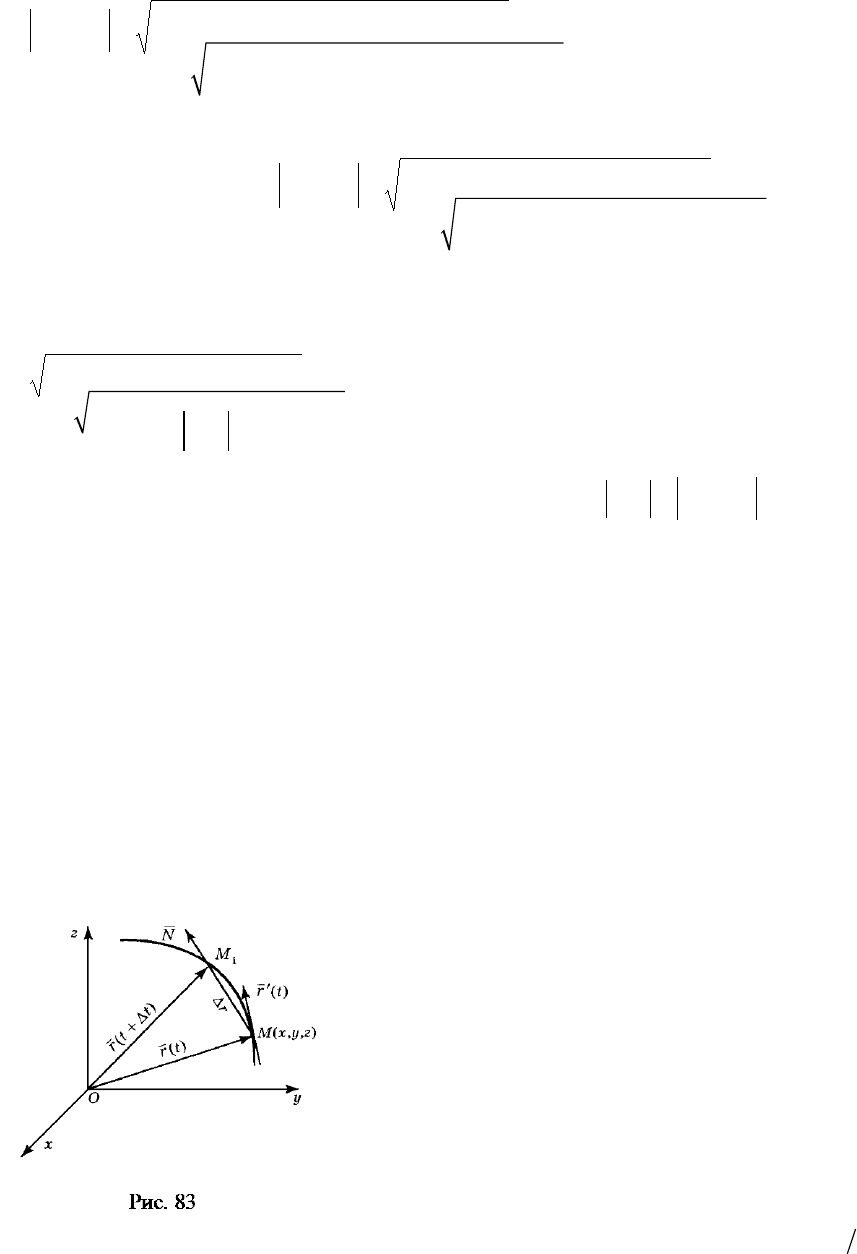
(см. рис. 83). Ясно, что

( ) ( ) ( ) ( )

rttxttiyttjzttk+∆ = +∆ + +∆ + +∆

 

. Обозначим

( ) ( ) ( ) ( )

r rt t rt x xt t xt

y yt t yt z zt t zt

∆ = +∆ − ∆ = +∆ −

 

Тогда

.r xi y j zk∆ =∆ +∆ +∆





Этот вектор умножим на число, равное

1,t∆

и пе-

рейдём к пределу при

0:t∆→

149

0 00 0 0

lim lim lim lim lim .

t tt t t

rx y z

r i jk

t tt t t

∆→ ∆→ ∆→ ∆→ ∆→

∆∆ ∆ ∆

⋅∆ = = + +

∆ ∆∆ ∆ ∆







(20)

Но

,x∆

,y∆

z∆

– приращения функций

( )

,xt

( )

,yt

( )

,zt

поэтому пределы от-

ношений правой части (20) равны соответственно

′

по определению

производной. Таким образом,

lim .

tt t

xi yj zk

∆→

∆

′′′

=++

∆







(21)

Левую часть этой формулы назовём производной от векторной функции

( )



из (16) и обозначим

( )

lim .

r rt

∆→

∆

′

= =

∆



 

(22)

Теперь (21) можно записать в виде

( )

() () ().

r t x ti y t j z tk

′

′′′

=++

 

(23)

Эта формула определяет производную от векторной функции

( )

,rt



заданной

(16). Выясним геометрический смысл этой производной. Предположим, что

0.t∆>

Тогда точка

с радиус-вектором

( )

rt t+∆



отвечает большему значе-

нию

tt+∆

параметра по сравнению с точкой

Значит, показанный на

рис. 83 вектор



направлен в сторону возрастания параметра

Имеем

( ) ( )

.MM rt t rt r= +∆ − =∆

   

Этот вектор умножим на положительное число

1 t∆

получим

/ /.r t MM t MN∆ ∆= ∆=

  

(24)

Согласно правилу умножения вектора на число, вектор



направлен как

вектор



и отличается от него только длиной. Заметим, что этот вектор

направлен по секущей

в сторону возрастания

В формуле (24) перей-

дём к пределу при

0:t∆→

0 0,

lim( / ) lim .

t t MM

r t MN

∆→ ∆→ →

∆∆=

 

Левая часть этой формулы

согласно (22) есть производная

( )

,rt



поэтому

( )

lim .

t MM

r t MN

∆→ →

′

 

Как было

замечено выше, вектор



направлен по секущей

в сторону возраста-

ния

В пределе эта секущая займёт положение касательной к кривой в точке

5354.ru

150

поэтому

( )

lim

r t MN

→

′

 

есть вектор, направленный по касательной к кри-

вой в её точке

в сторону возрастания параметра

Начало вектора

( )

′



условимся помещать в точке

Отметим, что так

как рассматриваемую кривую описывает конец вектора

( )

,rt



то векторное

уравнение этой кривой имеет вид

( )

,r rt=



(25)

а соотношения (19) представляют собой параметрические уравнения линии.

Правила дифференцирования векторной функции. Пусть даны две диффе-

ренцируемые векторные функции

( )

,r rt=

 

( )

,r rt=

 

т. е. функции, которые

имеют производные, вычисляемые по формуле (23). Для них справедливы

формулы

( )

12 1 2

;rr r r

′

′′

+=+

    

( )

12 1 2 12

, , ,;rr r r rr

′



′′

= +





       

( )

12 1 212

.rr r r rr

′

′′

× = ×+×

  

  

Эти соотношения устанавливаются непосредственной проверкой.

§ 6. Уравнения касательной прямой и нормальной плоскости

для пространственной кривой

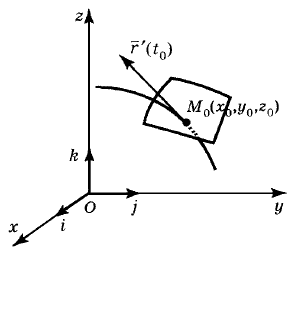
Пусть в пространстве

Oxyz

задана кривая пара-

метрическими уравнениями (19) (рис. 84). Поступая,

как и выше, от (19) перейдём к векторному уравне-

нию (25) этой кривой, в котором

( )



выражается

формулой (16).

Пусть

( )

0000

,,Mxyz

– фиксированная точка кри-

вой, отвечающая заданному значению параметра

,tt=

– заданное число. По этому числу найдем

координаты точки

, подставив

tt=

в формулу (19):

( ) ( )

0 00 0

,,x xt y yt= =

( )

.z zt=

Это будут известные нам числа. По формуле (23) вычислим

( )

′



–

производную векторной функции (16). Подставив значение

,tt=

отвечающее

точке

найдём вектор

( ) ( ) ( ) ( )

00 0 0

,rt xtiytjztk

′

′′′

=++

 

направленный по каса-

тельной к кривой в точке

Проекции этого вектора

( )

,xt

′

( )

,yt

′

( )

′

– из-

вестные числа. Зная проекции этого вектора, лежащего на касательной, и ко-

Рис. 84