Салимов Р.Б. Математика (для студентов бакалавриата)

Подождите немного. Документ загружается.

151

ординаты точки

касательной, запишем канонические уравнения этой ка-

сательной

( )

0 00

000

xx yy zz

xt yt zt

−−−

= =

′′′

(26)

Плоскость, проходящая через точку

перпендикулярно к касательной

рассматриваемой кривой, называется нормальной плоскостью для этой кри-

вой в точке

Зная координаты точки

и проекции нормального вектора

( )

′



для этой плоскости, получим уравнение этой нормальной плоскости:

( )( ) ( )( ) ( )( )

00 0 000

0.xtxx ytyy ztzz

′′′

−+ −+ −=

5354.ru

152

ГЛАВА 9. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

§ 1. Функции двух переменных и способы их задания

Пусть

– некоторое множество пар

( )

,xy

действительных чисел,

–

некоторое множество действительных чисел

Функцией двух переменных

,xy

называется правило, согласно которому

каждой паре чисел

( )

,xy

из множества

отвечает одно определённое число

из множества

при условии, что каждому числу

из множества

отве-

чает хотя бы одна пара

(, )xy

из множества

Числа

,xy

называют аргумен-

тами или независимыми переменными, а

– зависимой переменной или

функцией. Множество

называют областью определения функции, а мно-

жество

– областью значений функции.

Для обозначения функции применяют символ

( )

,z f xy=

. Например,

.zx y= +

Если конкретной паре аргументов

,xx=

yy=

отвечает определён-

ное значение

zz=

функции

( )

,,z f xy=

то пишут

( )

0 00

,z fxy=

или

Каждой паре чисел

(, )xy

на плоскости

Oxy

отвечает определённая точка

( )

,,Pxy

поэтому функцию двух переменных

( )

,z f xy=

можно рассматривать

как функцию точки

при этом пишут

( ) ( )

,,z f xy f P= =

помня, что

– точ-

ка с координатами

,.xy

Ясно, что множеству

– области определения функ-

ции

( ) ( )

,z f xy f P= =

– на плоскости

Oxy

отвечает некоторое множество точек.

Будем также называть его областью определения рассматриваемой функции.

Как правило, будем рассматривать функции двух переменных, для кото-

рых указанное множество точек, отвечающих

на плоскости

Oxy

образует

область.

Пусть плоскость

Oxy

разбита простой (т. е. без точек самопересечения)

замкнутой кривой

на две части: внутреннюю

внешнюю (см. рис. 88). Каждую из этих частей

называют областью, кривую

– границей области.

Точки области, не лежащие на границе

называ-

ются внутренними точками области, а точки гра-

ницы – граничными. Если в область входят также

все точки её границы

то эту область называют

153

замкнутой.

Область называется конечной (ограниченной), если все ее точки располо-

жены на конечном расстоянии от начала координат. Напимер, область

внутренняя для кривой

является конечной, а область, внешняя по отноше-

нию к кривой

– бесконечной. Другими примерами бесконечных областей

служат вся плоскость

Oxy

и верхняя полуплоскость с осью

в качестве гра-

ницы. В дальнейшем области, внешние к замкнутой кривой, не рассматрива-

ются. Строгое математическое определение области мы не приводим.

Способы задания функции двух переменных

Табличный способ задания функции заключается в том, что значения

функции задают с помощью таблицы. Например, таблица может иметь сле-

дующий вид: в первом столбце указывают ряд значений

а в первой строке

– ряд значений

На пересечении строк и столбцов записывают соответ-

ствующие значения функции

( )

,.f xy

\xy

...

( )

,fxy

( )

,fxy

...

( )

fxy

( )

,fxy

( )

,fxy

...

( )

fxy

...

( )

fxy

( )

fxy

...

( )

fxy

Аналитический способ задания функции – это способ задания функции

с помощью формул. Пусть, например, функция двух переменных задана фор-

мулой

1.z xy=−−

(1)

Если функция

( )

,z f xy=

задана одной формулой, без указания области

определения, то под областью определения понимают совокупность всех то-

чек

( )

,Pxy

плоскости

,Oxy

в которых по данной формуле можно найти соот-

ветствующее значение

( )

,,z f xy=

т. е. когда эта формула имеет смысл и поз-

воляет найти соответствующее значение функции.

Найдём область определения функции, заданной формулой (1). Ясно, что

в любой точке

( )

,Pxy

значение рассматриваемой функции можно найти, если

для координат

,xy

этой точки выражение под корнем положительно или рав-

но нулю, т. е.

10xy−−≥

или

5354.ru

154

1.xy+≤

(2)

Поскольку

222

,OP x y= +

то неравенство (2) записывается в

виде

1OP ≤

или

1.OP ≤

Таким образом, областью опреде-

ления функции (1) служит множество точек

расстояние

которых до начала координат меньше или равно 1, т. е.

круг с радиусом 1 и центром в начале координат (рис. 89).

Для всех точек границы этого круга имеем

222

1,OP x y=+=

поэтому в этих точках

0,z =

т. е. функция (1) определена также во всех точках

границы области определения. Значит, последняя есть замкнутая область.

§ 2. Геометрическое представление функции двух переменных

Пусть в области

плоскости

Oxy

пространства

Oxyz

задана функция

двух переменных

( ) ( )

,.z f xy f P= =

Через точку

( )

,Pxy

области

проведём

прямую, параллельную оси

(см. рис. 90). На этой прямой возьмем точку

( )

,, ,Mxyz

абсцисса

и орди-ната

которой

равны абсциссе

и ординате

точки

а ап-

пликата

равна значению

( ) ( )

,z f xy f P= =

функции в точке

. Это означает, что расстоя-

ние

( )

,z f xy= =

при

0,z >

когда точка

лежит выше плоскости

,Oxy

( )

,PM z f x y=−=−

при

0,z <

когда точка

лежит ниже плоскости

.Oxy

Такое построение выполним для всех точек

( )

,Pxy

области

Тогда в пространстве полу-

чим множество точек

( )

,, .Mxyz

Как правило будем рассматривать функции,

для которых это множество образует некоторую сплошную поверхность. Эту

поверхность будем называть графиком рассматриваемой функции

( )

,.z f xy=

По построению, координаты

,,xyz

любой точки

этой поверхности удо-

влетворяют соотношению

( )

,,z f xy=

следовательно, последнее соотношение

является уравнением этой поверхности.

Итак, мы показали, что каждой функции двух переменных

( )

,z f xy=

пространстве

Oxyz

отвечает поверхность с уравнением

( )

,.z f xy=

Это и есть

геометрическое истолкование функции двух переменных.

155

Например, функции, определённой формулой (1), в пространстве

Oxyz

от-

вечает верхняя часть сферы радиуса

1r =

с центром в начале координат. В са-

мом деле, согласно (1)

0,z ≥

т. е. поверхность расположена выше плоскости

,Oxy

а возведя в квадрат (1), получим уравнение сферы

222

1.xyz++=

Это

означает, что координаты любой точки, рассматриваемой поверхности, отве-

чающей функции (1), удовлетворяют последнему уравнению.

§ 3. Функции трёх и большего числа переменных. Частное и

полное приращения функции

Аналогично предыдущему можно ввести понятия функций трёх и боль-

шего числа переменных. Например, функции трёх переменных обозначаются

( )

,, .U f xyz=

Мы знаем, что в пространстве

Oxyz

тройке чисел

,,xyz

отвеча-

ет точка

( )

,, .Pxyz

Поэтому

( )

,,U f xyz=

можно рассматривать как функцию

точки

и писать

( ) ( )

,, .U f xyz f P= =

Как правило, будем рассматривать

функции трёх переменных, для которых областью определения служит неко-

торая конечная область - часть пространства

,Oxyz

ограниченная замкнутой

поверхностью (например, сферой). Эту поверхность называют границей обла-

сти. Определения конечной и замкнутой областей такие же, что и в § 1.

Функцию

переменных будем обозначать

( )

,,, ,

U fxx x= 

здесь

,,,

xx x

– аргументы функции. Мы знаем, что в

-мерном пространстве

каждой совокупности

чисел

,,,

xx x

отвечает точка

для которой эти

числа являются координатами. Поэтому функцию

переменных можно рас-

сматривать как функцию этой точки

-мерном пространстве

( )

.U fP=

Функции трёх и большего числа переменных геометрического истолкования

не имеют.

Пусть дана функция двух переменных

( )

,.z f xy=

Пусть из двух аргумен-

тов этой функции второй аргумент

– постоянная, а первый аргумент

из-

меняется и получает приращение

.x∆

Тогда соответствующее приращение

функции обозначается

( )

z f x xy∆ = +∆ −

( )

,f xy−

и называется частным при-

ращением по

функции

( )

,z f xy=

в точке

( )

,xy

соответствующим прира-

щению

.x∆

Пусть теперь

const,x =

изменяется и получает приращение

.y∆

Тогда

соответствующее приращение функции обозначается

( ) ( )

z f xy y f xy∆ = +∆ −

5354.ru

156

и называется частным приращением по

функции

( )

,z f xy=

в точке

( )

,xy

соответствующим приращению

.y∆

Пусть теперь оба аргумента

,xy

изменяются и получают приращения

,.xy∆∆

Тогда выражение

( ) ( )

,,z f x xy y f xy∆ = +∆ +∆ −

называется полным при-

ращением функции

( )

,z f xy=

в точке

( )

,xy

, соответствующим приращениям

,.xy∆∆

Аналогично определяются частное и полное приращения функции трёх

и большего числа переменных.

Рассмотрим функцию

переменных

( )

,,, .

U fxx x= 

Пусть изменяется

только

и получает приращение

,x∆

а все остальные аргументы остаются

постоянными. Тогда эта функция получает частное приращение по

( ) ( )

1 12 12

,,, ,,, .

x nn

U fx xx x fxx x∆ = +∆ −

Если изменяются все аргументы этой

функции, то получаем её полное приращение

( ) ( )

1 12 2 12

, ,, ,,, .

nn n

U fx xx x x x fxx x∆ = +∆ +∆ +∆ −

§ 4. Предел функции

Пусть в некоторой области

плоскости

Oxy

задана функция

( ) ( )

,,z f xy f P= =

( )

000

,Pxy

– фиксированная точка области

,xy

– задан-

ные числа, а

( )

,Pxy

– переменная точка этой области. Положим, что точка

стремится к точке

произвольно. Пусть при этом значение функции в точке

стремится к некоторому значению

в том смысле, что

( )

0.fP b−→

этом случае число

называют пределом функции

( )

.fP

Чтобы дать строгое

определение предела, введём следующие понятия.

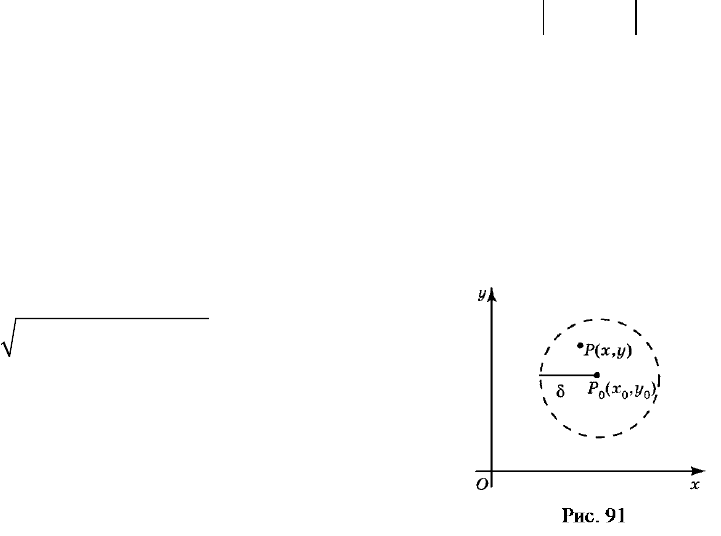
Окрестностью точки

называется внутренность круга с центром в точ-

ке

Если радиус круга равен

то окрестность называют

-окрестностью

точки

(см. рис. 91). Ясно, что для любой точки

( )

,Pxy

-окрестности точ-

ки

расстояние от точки

до точки

меньше

т. е.

или

( ) ( )

.xx yy

− +− <

Теперь можно

записать строгое определение вышеуказанного преде-

ла.

Число

называется пределом функции

( ) ( )

,z f xy f P= =

при

( )

,Pxy

, стремящемся к

( )

000

,,Pxy

157

если для любого положительного числа

каким бы малым оно ни было,

найдутся такое положительное число

и соответствующая

-окрестность

точки

что для всех точек

( )

,Pxy

этой окрестности (за исключением, воз-

можно, точки

) выполняется неравенство

( )

fP b

−<

или

( )

,.f xy b

−<

(3)

В этом случае будем писать

( )

lim fP b

→

или

( )

lim , .

xxyy

f xy b

→→

Из приведенного определения ясно, что речь идёт о пределе функции

( ) ( )

,,z f xy f P= =

когда точка

( )

,Pxy

стремится к

( )

000

,Pxy

по произвольному

пути, так как (3) выполняется для всех точек

( )

,Pxy

-окрестности точки

Если предел функции

( )

при

PP→

равен нулю, то

( )

называют беско-

нечно малой функцией при

.PP→

Легко проверить, например, что функция

zx y

= +

является бесконечно малой при

( ) ( )

, 0, 0 ,Pxy P→

т. е.

( )

0, 0

lim 0.

→→

Замечание. Согласно определению предела функции неравенства (3)

должны выполняться для всех точек

( )

,Pxy

из окрестности точки

. В про-

тивном случае функция предела не имеет. Возьмем, например, функцию

22 22

( )/( )zxy xy=−+

и рассмотрим её поведение при

( ) ( )

, 0, 0 .Pxy P→

В любой

окрестности точки

для всех точек, лежащих на

,Ox

для которых

0,y =

име-

ем

1.z =

Для всех точек оси

этой окрестности, для которых

0,x =

получаем

1.z = −

Таким образом, неравенство (3) не может выполняться ни для одного

числа

в окрестности точки

Это означает, что указанная функция при

PP→

предела не имеет.

Определение предела функции трёх и большего числа переменных анало-

гично определению предела для функции двух переменных. Нужно только

ввести понятие окрестности точки

Сделаем это для случая функции

пе-

ременных

( )

,,, .

U fxx x= 

Введём

-мерное пространство, в котором возь-

мём переменную точку с координатами

( )

,,, .

xx x

Пусть в

-мерном про-

странстве

– фиксированная точка. Её координаты обозначим

( )

00 0

01 2

,,, ,

Pxx x

где

00 0

,,,

xx x

– заданные числа;

-окрестностью точки

этом

-мерном пространстве будем называть множество всех точек

5354.ru

158

( )

,,, ,

Px x x

расстояние от которых до

меньше

т. е.

.PP

Иначе го-

воря,

( ) ( ) ( )

222

000

11 2 2

xxxxxx

−+−+−<

Для предела функции многих переменных справедливы все теоремы, до-

казанные для предела функции одной переменной. Они формулируются и до-

казываются аналогично.

§ 5. Непрерывность, точки и линии разрыва функций

Функция многих переменных

( )

U fP=

называется непрерывной в точке

если

( ) ( )

lim .

fP fP

→

(4)

Это означает, что:

• существует

( )

,fP

т. е. функция

( )

определена в точке

и всюду

вблизи нее;

• существует предел

( )

lim fP

→

;

• этот предел равен значению функции

( )

.fP

Для непрерывных функций многих переменных справедливы теоремы о

непрерывности алгебраической суммы, произведения, частного непрерывных

функций, а также теорема о непрерывности сложной функции, составленной

из непрерывных функций, доказанные ранее для функций одной переменной.

Эти теоремы формулируются и доказываются аналогично случаю функций

одной переменной. Условие (4) для функций двух переменных, например,

можно записать, выделив аргументы следующим образом:

( ) ( )

lim , , ,

xxyy

fxy fxy

→→

(5)

где

,xy

– координаты точки

,xy

– координаты точки

стремящейся к

точке

При

,xx→

,yy→

т. е. когда переменными являются

,,xy

( )

,fxy

–

постоянная. Но предел постоянной равен этой постоянной, т. е.

( ) ( )

00 00

, lim , .

xxyy

fxy fxy

→→

Этот предел подставим в правую часть выражения

(5), затем предел перенесём влево и разность пределов в левой части запишем

159

как предел разности:

( ) ( )

lim , , 0.

xxyy

fxy fxy

→→

−=





Обозначим

,xx x−=∆

.yy y−=∆

Тогда

,xx x= +∆

.yy y= +∆

Таким образом, получим

( ) ( )

0 0 00

lim , , 0.

xxyy

fx xy y fxy

→→

+∆ +∆ − =





Здесь выражение в квадратных скобках есть полное приращение

z∆

функции

( )

,z f xy=

в точке

( )

,.xy

Итак, формула принимает окончательно вид

0, 0

lim 0.

∆→ ∆→

∆=

Таким образом, если функция

( )

,z f xy=

непрерывна в точке

( )

000

,,Pxy

то

полное приращение

z∆

этой функции в точке

соответствующее прираще-

ниям

,,xy∆∆

стремится к нулю, когда

0x∆→

0y∆→

одновременно. Это

утверждение справедливо и для функций трёх и большего числа переменных.

Его можно принять за второе определение непрерывности функции в точке.

Точка

называется точкой разрыва функции

( )

U fP=

многих перемен-

ных, если в этой точке нарушается хотя бы одно из трёх вышеуказанных

условий непрерывности. Так, для функции двух переменных

( )

,z f xy=

таких

точек разрыва может быть несколько и даже бесконечное множество. В част-

ности, такие точки разрыва на плоскости

Oxy

могут образовать даже линии.

Эти линии называются линиями разрыва функции двух переменных

( )

,z f xy=

(для функции трёх переменных

( )

,,U f xyz=

в пространстве

Oxyz

точки раз-

рыва могут образовывать поверхности разрыва). Например, для функции двух

переменных

1/( )z yx= −

линией разрыва на плоскости

Oxy

служит прямая

.yx=

В самом деле, для всех точек этой прямой имеем

0yx−=

и в них функ-

ция

не определена. Нарушается первое условие в определении непрерыв-

ности функции.

§ 6. Свойства функций, непрерывных в конечной

(ограниченной) замкнутой области

Функция

( )

U fP=

называется непрерывной в области, если она непре-

рывна в каждой точке этой области. Функция называется непрерывной в за-

мкнутой области, если она непрерывна во всех точках области, включая точ-

ки границы области (см. § 1).

Приведем без доказательства следующее утверждение.

5354.ru

160

Теорема 1. Если функция непрерывна в замкнутой конечной (ограничен-

ной) области, то:

• по крайней мере в одной точке

области она принимает своё

наибольшее значение

( )

,M fP=

удовлетворяющее условию

( ) ( )

fP fP≥

для

всех точек

области, и по крайней мере в одной точке

области эта

функция принимает наименьшее значение

( )

,m fP=

удовлетворяющее для

всех точек

области условию

( ) ( )

fP fP≤

;

• любое значение

заключённое между

функция принимает по

крайней мере в одной точке области.

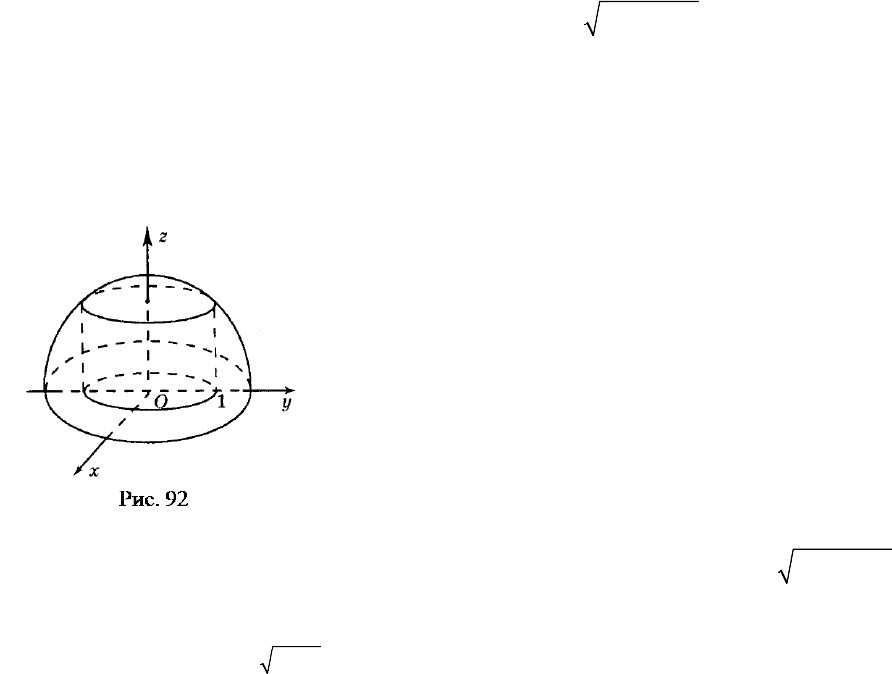
Проиллюстрируем эту теорему на примере функции

1.z xy=−−

(6)

Она определена в замкнутой конечной области – круге радиуса

1r =

с цен-

тром в начале координат. Граница круга входит в область определения. Гра-

фик этой функции – верхняя часть сферы радиуса

1r =

с центром в начале ко-

ординат.

Функция принимает наибольшее значение, рав-

ное 1, в точке

( )

0 0, 0 .

В самом деле, как видно из

формулы (6), во всех остальных точках значения

функции будут меньше 1, так как

11xy−−<

Наименьшее значение, равное нулю, функция при-

нимает в точках границы области определения – на

окружности с уравнением

1.xy+=

Любое значе-

ние

0 1,

≤≤

эта функция принимает в точках

( )

,,xy

для которых

в формуле (6) равно

т. е.

1 xy

=−−

или

22 2

1.xy

+=−

Эти точки образуют окружность с центром в начале координат

( )

0, 0

и радиусом

= −

(рис. 92).

§ 7. Частные производные

Дана функция

( )

,.z f xy=

Частной производной по

этой функции назы-

вается её производная по

вычисленная в предположении, что

const.y =

Эта

частная производная по

обозначается

′

либо

/,zx∂∂

либо

( )

f xy

′

либо

( )

, /.f xy x∂∂

Поскольку мы считаем, что

остается постоянной, то получим