Салимов Р.Б. Математика (для студентов бакалавриата)

Подождите немного. Документ загружается.

161

функцию

( )

,z f xy=

одного аргумента

Указанную производную определим

известным способом – для данного приращения

x∆

возьмем приращение рас-

сматриваемой функции. Оно будет частным приращением по

так как

const:y =

( ) ( )

, ,.

z f x xy f xy∆ = +∆ −

Согласно определению производной

lim .

∆→

∆

∂

′

= =

∂∆

(7)

Частной производной по

функции

( )

,z f xy=

называется её производная

по

вычисленная в предположении, что

остается постоянной. Эта произ-

водная обозначается

′

либо

/,zy∂∂

либо

( )

f xy

′

либо

( )

,/f xy y∂∂

и по ана-

логии с предыдущим определяется формулой

lim ,

∆→

∆

∂

′

= =

∂∆

(8)

где

( ) ( )

, ,.

z f xy y f xy∆ = +∆ −

(9)

Аналогично определяются частные производные функций

переменных.

Пусть дана функция

( )

,,,

U fxx x= 

переменных. Пусть изменяется

только

а все остальные аргументы остаются постоянными. Тогда мы мо-

жем вычислить частную производную по

этой функции

( )

, , , lim .

xx n

U f xx x

∆→

∆

∂

′′

= = =

∂∆



Пример. Найти частные производные функции

zx=

Частная ее производная по

вычисляется в предположении, что

const.y =

Тогда получим степенную функцию вида

, поэтому

z yx

−

′

Частная про-

изводная по

этой функции берётся при

const,x =

т. е. мы получим показа-

тельную функцию вида

, следовательно,

ln .

zxx

′

§ 8. Геометрический смысл частных производных функции двух

переменных

Дана функция

( )

,,z f xy=

ей в пространстве

Oxyz

соответствует поверх-

ность (см. рис. 93), для простоты считаем, что

( )

, 0.f xy>

Через произвольную

точку

оси

проведём плоскость перпендикулярно к

.Ox

Она пересекает

поверхность

( )

,z f xy=

по линии

а плоскость

Oxy

– по прямой

.PP

Все

5354.ru

162

точки этой плоскости имеют одну и ту же

абсциссу

Пусть

,xy

– координаты точки

а точка

имеет координаты

( )

,.xy y+∆

Рассмотрим случай, когда

0.y∆>

В точке

( )

,Pxy

найдём значение заданной функции

( )

,.f xy

Это значение равно

– расстоя-

нию от точки

до точки

поверхности.

Значение

( )

,f xy y+∆

заданной функции в

точке

равно

– расстоянию от точки

до точки

поверхности. Раз-

ность этих значений

( ) ( )

,,f xy y f xy+∆ −

z= ∆

есть частное приращение функ-

ции

( )

,z f xy=

в точке

( )

,,Pxy

соответствующее приращению

.y∆

Это значе-

ние равно расстоянию

.KM

Пусть

– угол, образованный секущей

линии

с прямой

или с

осью

,Oy

так как последняя параллельна прямой

.PP

Из рис. 93 видно, что

/ tg .

∆ ∆=

(10)

При

0y∆→

точка

стремится к точке

по кривой

секущая

стре-

мится к положению касательной

к кривой

в точке

стремится к

– углу, образованному этой касательной с прямой

,PP

т. е. с осью

.Oy

Пе-

рейдя в (10) к пределу при

0y∆→

, получим

lim lim tg .

∆→ ∆→

∆

(11)

Но

– непрерывная функция при

0 /2

ϕπ

, поэтому

limtg tg .

ϕβ

→

Подста-

вим последнее выражение в правую часть (11) и учтём, что левая часть (11),

согласно (8), равна

′

, следовательно,

tg .

′

Итак, частная производная по

от функции

( )

,z f xy=

равна тангенсу уг-

ла

образованного с осью

касательной к линии

в её точке

Анало-

гично устанавливается геометрический смысл частной производной по

функции

( )

,.z f xy=

Рис. 93

163

§ 9. Полный дифференциал

Дана функция двух переменных

( )

,.z f xy=

Будем считать, что она имеет

непрерывные частные производные и в точке Мы зна-

ем, что полное приращение определяется формулой

(12)

В правой части этой формулы прибавим и вычтем Получим

. (13)

Разность двух значений функции при одном и том

же

можно записать по формуле Лагранжа для функции одной переменной в

виде считая в нашем случае

Кроме того, вместо мы должны взять частную производную в точке

лежащей между и Получим

(14)

Для первой разности в правой части (13) (для фиксированного ) запи-

шем аналогично

Здесь – точка, лежащая между и Это выражение и выражение (14)

подставим в (13), будем иметь

(15)

При очевидно поэтому и

При этом, так как частные производные в правой части формулы (15) непре-

рывны в точке по условию, то пределы этих производных равны их зна-

чениям в предельной точке, т. е.

( ) ( )

lim .

f xy f xy

→

∂∂

( )

f xy

( )

f xy

( )

,.xy

( ) ( )

, ,.z f x xy y f xy∆ = +∆ +∆ −

( )

,.f xy y+∆

z∆=

( ) ( ) ( ) ( )

,, ,,f x xy y f xy y f xy y f xy= +∆ +∆ − +∆ + +∆ −

  

  

( ) ( )

,,f xy y f xy+∆ −

( )

,f xy

( ) ( ) ( )( )

,,fb fa f cb a a c b

′

− = − <<

,by y= +∆

.ay=

( )

′

.yy+∆

( ) ( )

( )

,, .

f xy

f xy y f xy y

∂

+∆ − = ⋅∆

∂

yy+∆

( ) ( )

( )

,, .

f xy y

f x xy y f xy y x

∂ +∆

+∆ +∆ − +∆ = ⋅∆

∂

.xx+∆

( )

,,f xy y f xy

z xy

∂ +∆ ∂

∆ = ⋅∆ + ⋅∆

∂∂

0,x∆→

0y∆→

( )

,xx x+∆ →

( )

,yy y+∆ →

xx→

.yy→

( )

,xy

( ) ( )

lim ,

yyy

fxy y fxy

→

+∆ →

∂ +∆ ∂

∂∂

5354.ru

164

Из теории пределов известно, что функцию можно представить в виде суммы

её предела и бесконечно малой функции, поэтому

где – бесконечно малые функции, стремящиеся к нулю при и ,

одновременно стремящихся к нулю. Теперь (15) можно записать так:

(16)

Обозначим

( ) ( ).rxy∆= ∆ +∆

Последнее выражение возведём в квадрат и за-

тем поделим на:

22 2

():(/)(/)1

r xr yr∆ ∆ ∆ +∆ ∆ =

или

|/||/|1.xr yr∆ ∆ +∆ ∆ =

Отсюда

видно, что

| / |1xr∆ ∆≤

| / | 1,yr∆ ∆≤

так как сумма квадратов этих выражений

равна 1. Очевидно, что величины

/xr∆∆

/yr∆∆

являются ограниченными

функциями от в частности, при и одновременно.

Покажем, что предел

lim[( )/ ] 0.

x yr

γγ

∆→

⋅∆ + ⋅∆ ∆ =

В самом деле,

/xr∆∆

–

ограниченная функция, а – бесконечно малая функция при и

одновременно. Но произведение бесконечно малой функции и ограниченной

функции есть бесконечно малая функция, следовательно,

(/)xr

∆ ∆⋅

– беско-

нечно малая функция при и одновременно. Аналогично

(/) 0yr

∆ ∆⋅ →

при и Значит,

( )/x yr

γγ

⋅∆ + ⋅∆ ∆

также есть бес-

конечно малая функция при и одновременно. Таким образом,

сумма есть бесконечно малая функция более высокого порядка,

чем

r∆

, при

0r∆→

(образно говоря, эта сумма стремится к нулю «быстрее»,

чем

r∆

Функция называется дифференцируемой в точке если

для ее полного приращения справедлива формула (16), в которой сумма

есть бесконечно малая функция более высокого порядка, чем

.r∆

При этом сумма первых двух слагаемых в правой части (16) называется пол-

ным дифференциалом функции и обозначается Итак, полный

дифференциал функции определяется формулой

(17)

В силу последнего обозначения соотношение (16) примет вид

( )

f xy y

f xy

∂ +∆

∂

= +

∂∂

( )

f xy

∂

= +

∂∂

γγ

x∆

y∆

( ) ( )

f xy f xy

z x yxy

γγ

∂∂

∆ = ⋅∆ + ⋅∆ + ⋅∆ + ⋅∆

∂∂

,x∆

,y∆

0x∆→

0y∆→

0x∆→

0y∆→

0x∆→

0y∆→

0x∆→

0.y∆→

0x∆→

0y∆→

γγ

⋅∆ + ⋅∆

(,)z fxy=

( )

,,xy

γγ

⋅∆ + ⋅∆

( )

,z f xy=

.dz

( )

,z f xy=

( ) ( )

f xy f xy

dz x y

∂∂

= ⋅∆ + ⋅∆

∂∂

165

(18)

В случае, когда функция имеем При этом

и Совершенно аналогично, взяв , получим, что

Иначе говоря, приращения независимых переменных равны их пол-

ным дифференциалам, и в формуле (17) можно взять вместо и вме-

сто

.y∆

Из равенства (16) следует, что если функция

(,)fxy

имеет непрерыв-

ные частные производные в данной точке, то она дифференцируема в этой

точке и имеет полный дифференциал (17).

Рассмотрим функцию переменных. Ее полное прира-

щение

Полный дифференциал этой функции определяется формулой, аналогичной

(17):

ff f

dU x x x

xx x

∂∂ ∂

= ∆+ ∆+ + ∆

∂∂ ∂



Пусть теперь функция имеет непрерывные частные произ-

водные по всем аргументам в точке -мерного

пространства. Тогда, поступая так же, как и в случае функции двух перемен-

ных при выводе формулы (16), можно показать, что

где – бесконечно малые функ-

ции, когда стремится к нулю

22 2

( ) ( ) ( ).

rx x x∆ = ∆ +∆ + +∆

§ 10. Применение полного дифференциала функции

в приближённых вычислениях

Для полного приращения функции мы получили формулу (18),

в которой есть бесконечно малая функция более высокого поряд-

ка, чем

r∆

когда

0.r∆→

Это означает, что при малых значениях сум-

ма будет значительно меньше, чем

,r∆

поэтому указанной сум-

мой можно пренебречь. В результате получим приближённое соотношение

(19)

.z dz x y

γγ

∆ = + ⋅∆ + ⋅∆

( )

,,z f xy x= =

.dz dx=

( )

, 1,

f xy=

( )

f xy=

.dx x= ∆

( )

,z f xy y= =

.dy y= ∆

x∆

( )

, ,...,

U fxx x=

( ) ( )

1 12 2 12

, ,..., , ,..., .

nn n

U fx xx x x x fxx x∆ = +∆ +∆ +∆ −

( )

, ,...,

fxx x

, , ...,

xx x

( )

, , ...,

xx x

112 2

... ,

U dU x x x

γγ γ

∆ = + ⋅∆ + ⋅∆ + + ⋅∆

, , ...,

γγ γ

( )

,z f xy=

γγ

⋅∆ + ⋅∆

,xy∆∆

γγ

⋅∆ + ⋅∆

,z dz∆≈

5354.ru

166

т. е. при малых полное приращение функции приближённо можно

заменить полным дифференциалом этой функции. Это свойство использу-

ется в приближённых вычислениях. В формулу (19) подставим выражение

(12) для и выражение (17) для и получим

Эта формула позволяет вычислить приближённое значение функции

в «новой» точке зная значения самой функции и ее

частных производных в «старой» точке Запишем последнюю формулу

для функции

Пример. Необходимо вычислить приближенно величину . Поло-

жим Получим

§ 11. Производная сложной функции

Дана функция

(20)

в которой аргументы в свою очередь являются функциями переменных

т. е.

(21)

Это означает, что в конечном счёте является функцией переменных :

(22)

Иначе говоря, является сложной функцией от . Нужно найти частные

производные этой функции, не выражая через т. е. не переходя к

(22), а имея лишь исходные функции (20) и (21). Будем считать, что функции

(20), (21) имеют непрерывные частные производные по всем своим аргумен-

там. Пусть а изменяется только и получает приращение Тогда

функции получают частные приращения

. (23)

,xy∆∆

z∆

( ) ( )

( )

,, .

f xy f xy

f x xy y f xy x y

∂∂

+∆ +∆ ≈ + ⋅∆ + ⋅∆

∂∂

( )

,f xy

( )

,,x xy y+∆ +∆

( )

,.xy

( )

z f xy x= =

( )

ln .

yy y

x x x yx x x x y

+∆

−

+∆ ≈ + ⋅ ⋅∆ + ⋅ ⋅∆

1.02

(1.01)

1,x =

1,y =

0, 01,x∆=

0,02.y∆=

( )

1,02

10 1

1,01 1 1 1 0,01 1 ln1 0,02≈ +⋅ ⋅ + ⋅ ⋅

( )

1,02

1,01 1 0,01 1,01.≈+ =

( )

,,z FUV=

,UV

,,xy

( )

,,U xy

( )

,.V xy

,xy

( ) ( )

,, , .z F xy xy

ϕψ





,xy

′′

,,xy

consty = ,

.x∆

( )

,,U xy

( )

,V xy

( ) ( ) ( ) ( )

, ,, , ,

U x xy xy V x xy xy

ϕϕ ψψ

∆ = +∆ − ∆ = +∆ −

167

Так как имеют непрерывные частные производные, то для

и справедливы представления, аналогичные (16), поэтому при

будем иметь и

Приращениям и аргументов и функции отвечает

полное приращение этой функции, которое мы можем записать по форму-

ле, аналогичной (16), в силу непрерывности частных производных от функ-

ции Для этого в (16) заменим на – на а –

на и Получим

(24)

здесь при Но формула (24) получена в предпо-

ложении, что поэтому – частное приращение по этой функции

зависящей от Значит, в данном случае Подставим вместо

в (24) и поделим полученное соотношение на тогда будем иметь

(25)

Но при величины стремятся к нулю. Перейдём в соот-

ношении (25) к пределу при Предел правой части будет равен сумме

пределов слагаемых, каждый из последних пределов равен произведению

пределов сомножителей. Кроме того,

Производную

/zy∂∂

найдем, поступив аналогично. Таким образом,

(,) (,)

z FUV U FUV V

x Ux Vx

z FUV U FUV V

y Uy Vy

∂∂∂∂∂



= +



∂ ∂∂ ∂∂





∂∂∂∂∂



= +

∂ ∂∂ ∂∂





(26)

Формулы (26) позволяют вычислить производные сложной функции зави-

сящей от когда эта функция задаётся формулами (20), (21).

Пример 1. Дана сложная функция где По

формулам (26) имеем

( )

,,xy

( )

,xy

U∆

V∆

0x∆→

U∆→

V∆→

U∆

V∆

( )

,z FUV=

z∆

( )

,.z FUV=

,xy

,,UV

,xy∆∆

U∆

V∆

( ) ( )

x xx x

FUV FUV

z U VUV

γγ

∂∂

∆ = ⋅∆ + ⋅∆ + ⋅∆ + ⋅∆

∂∂

0, 0

γγ

→→

0, 0.

UV∆→ ∆→

consty = ,

z∆

,.xy

zz∆=∆

z∆

,x∆

( )

x x xx x

FUV FUV

z U VUV

xUx Vx x x

γγ

∂∂

∆ ∆ ∆∆ ∆

= ⋅+ ⋅+⋅+⋅

∆∂∆ ∂∆ ∆ ∆

0x∆→

, ,,

γγ

∆∆

0.x∆→

lim ,

∆→

∆∂

′

= =

∆∂

lim

∆→

∆

∂

∆∂

lim .

∆→

∆

∂

∆∂

,,xy

sin ,

ze V=

,U xy= ⋅

Vx y

= +

5354.ru

168

Пусть теперь в формуле (20) и зависят лишь от т. е.

(27)

Здесь – функции одного аргумента поэтому в конечном счёте тоже

будет функцией одного аргумента При этом для производной по остаёт-

ся в силе первая формула (26) (так как все предыдущие утверждения сохра-

няют силу), но только производные по от будут не частными, а

обычными производными. В результате будем иметь

(28)

Пусть в (27) т. е.

(29)

Тогда для производной формула (28) примет вид

(30)

Заметим, что в этой формуле слева стоит полная производная а справа –

частная производная

.// xzxF ∂∂=∂∂

Пример 2. Дана функция По формуле (30) имеем

cos

/ 2 ( sin ) 2 ( sin )

dz dx x e x x e x=+− =+ −

Если … , то, поступив

аналогично предыдущему, придём к формуле

§ 12. Дифференцирование функций, заданных неявно

Дано соотношение

(31)

в котором есть известное выражение, содержащее Это соотноше-

ние определяет неявную функцию Нужно найти производную

этой функции. Запишем соотношение (31), обозначив левую часть через

sin cos 2 , sin cos 2 .

UU UU

eVyeVx eVxeVy

∂∂

=⋅ ⋅+⋅ ⋅ =⋅ ⋅+⋅ ⋅

∂∂

( )

,,z FUV=

( )

,Ux

( )

.Vx

( ) ( )

FUV FUV

dz dU dV

dx U dx V dx

∂∂

= ⋅+ ⋅

∂∂

,Ux=

( ) ( )

,, .z F xV V x

= =

′

( )

F xV F xV

dz dV

dx x V dx

∂∂

=+⋅

∂∂

,dz dx

, cos .

z x eV x=+=

( )

, ,..., ,

z FU U U=

( ) ( )

11 22

,,U xU x

ϕϕ

= =

( )

... .

dU dU

dz F F F

dx U dx U dx U dx

∂∂ ∂

= ⋅ + ⋅ ++ ⋅

∂∂ ∂

( )

, 0,Fxy=

( )

,Fxy

,.xy

( )

.yx

′

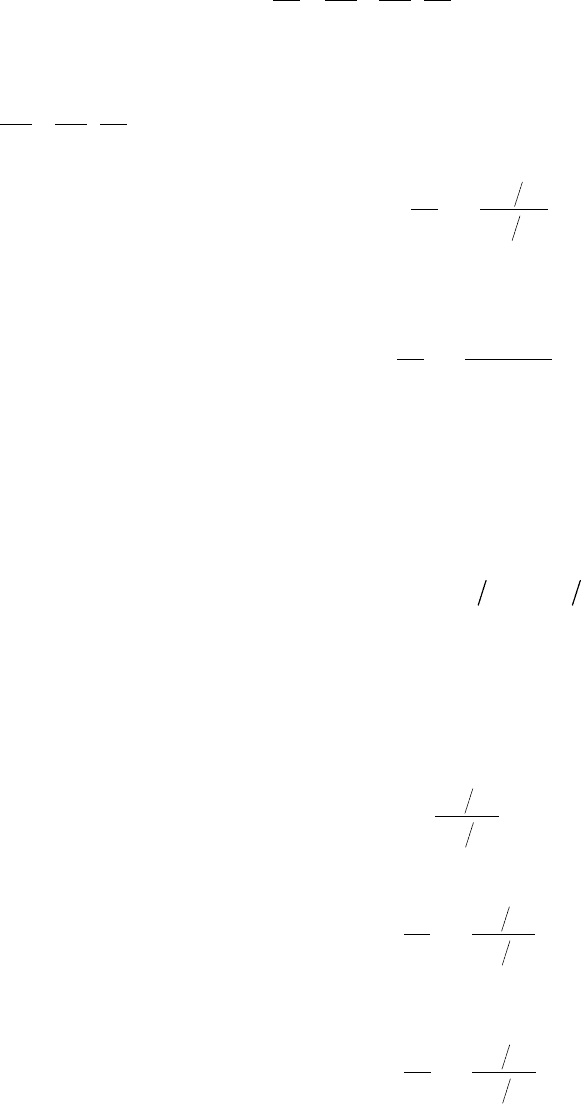
169

где Возьмём производную по от функции

в которой при этом учтем, что – функция от Запишем эту произ-

водную по формуле (30), заменив на

на

Так как при любом , то и её производная будет тождественно равна ну-

лю, т. е. Отсюда найдем производную

(32)

Эту формулу с помощью других символов производной можно записать так:

(33)

Рассмотрим теперь функцию двух переменных и , заданную неявно

соотношением

(34)

Нам необходимо найти частные производные и зная лишь (34). В

соотношении (34) положим Тогда функция будет зависеть лишь от

Таким образом, мы оказываемся в той же ситуации, что и ранее (когда бы-

ло задано соотношение (31)), только теперь роль играет так как –

функция от Производную можем вычислить по формуле (32), в которой

вместо должны взять Получим но производная здесь

частная производная, так как считаем, что Итак,

(35)

Аналогично найдём

(36)

В формулах (35) и (36) в правых частях можно использовать и другие обозна-

чения частных производных, тогда получим

( )

, 0,t Fxy= =

( )

.yx

( )

,,t Fxy=

( )

,yx

dt F F dy

dx x y dx

∂∂

=+⋅

∂∂

0t =

F F dy

x y dx

∂∂

+ ⋅=

∂∂

dy F x

dx F y

∂∂

= −

∂∂

( )

F xy

′

= −

′

( )

, , 0.Fxyz=

zx∂∂

,zy∂∂

const.y =

′

∂∂

′

= −

∂∂

′

const.y =

z Fx

x Fz

∂ ∂∂

= −

∂ ∂∂

z Fy

y Fz

∂ ∂∂

= −

∂ ∂∂

5354.ru

170

( )

,, ,,

F xyz

x F xyz y F xyz

′

∂∂

=−=−

′′

∂∂

(37)

Здесь в правой части есть значение, отвечающее паре согласно (34).

Пример. Пусть – функция двух аргументов, заданная соотношением

(38)

Здесь По формулам (35) и (36) имеем

∂

= −

∂

Найдем, например, значение при и Как видно из (38), паре

чисел отвечает поэтому

§ 13. Частные производные высших порядков

Дана функция Пусть она имеет частные производные

при этом каждая из них в свою очередь есть

функция от и Например, Поэтому от

каждой из указанных частных производных в свою очередь можно взять

частные производные как по так и по если они существуют. Эти произ-

водные называются вторыми частными производными или частными произ-

водными второго порядка от функции и обозначаются так:

xy xy yx yx

zz zz

zf zf

y x xy x y yx



∂∂ ∂ ∂∂ ∂



′′ ′′ ′′ ′′

= = = = = =



∂ ∂ ∂∂ ∂ ∂ ∂∂



В последних формулах на первом месте пишется та переменная, по которой

вначале проводится дифференцирование.

В качестве примера найдём вторые производные функции Снача-

ла находим отсюда

2 2 0.

xy z

eze+ −+ =

( )

,, 2 2 .

xy z

Fxyz e z e= + −+

z ey

∂⋅

= −

∂+

/zx∂∂

0x =

0.y =

0,x =

0y =

0,z =

z ey

∂⋅

=−=

∂+

( )

,.z f xy=

( )

/ ,,

z x f xy

′

∂ ∂=

( )

/ ,,

z y f xy

′

∂ ∂=

,z xy=

/ 3,z x yx∂ ∂=

/ 3.z y xy∂ ∂=

( )

,z f xy=

xx xx

zzf

xx x

∂∂ ∂



′′ ′′ ′′

= = = =



∂∂ ∂



yy yy

zzf

yy y



∂∂ ∂

′′ ′′ ′′

= = = =



∂∂ ∂



.z xy=

' 23

z xy=

' 32

z xy=

'' 3

z xy=

'' 3

z yx=

'' 2 2

z xy=

'' 2 2

z xy=