Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques

6.2. NETWORKS OF INFERENCE - J. PEARL'S BOOK

217

6.2.2 Independence

relations

All material in Section 6.2.2 is taken from [Pea88], Chapter 3 - sometimes in

slight reformulation - except the representation of the properties of Theorem 6.50

by arrow manipulation, which is due to the present author.

The probabilistic case (Section 3.1 in Pearl's book)

Let a probability measure P : IIN --~ [0, 1] be given.

Definition 6.49 P defines a 3-place relation < X I Y] Z >p on P(N) by

Vz e

IIX,

Vy e

IIy, Vz

e IIZ

if

y r 0

(P(y,z) > O + P(z ] y) = P(x [ y,z ))

< X } y I

Z

>e~ Vz e IIA', Vz 9 IIZ if Y = 0

(P(z) > o ~ P(~) = P(~ I z))

Ify=0, we shall also write < X ][ Z >p for <X[YIZ>p.

Theorem 6.50 If < X [ y ] Z >• is defined by some such P (i.e. < X y

Z >R iff < X I Y I Z >p), the following holds:

a) Symmetry: < X

l YFZ >R ~ < z

l YtX >R,

b) Decomposition: <2(lY]ZUW>n~ <X[YlZ>n,

c) Weak Union: < X I Y I Z U W >R --' < X 1 Y U W I Z >R,

d) Contraction: < X I 32 1 Z >s and < X I Y @Z ] W >R --+ < X y

ZUW>n.

If/~ is strictly positive, the following also holds:

e) Intersection: < 2t'lYUW] Z >R and < X i YUZ I W >n--* < X y

ZUW

>• (X C_/A etc.).

The proof is elementary. []

The author was quite surprised to notice that the above five axioms have a quite

natural representation as rules on labelled arrows: (We have sometimes combined

several axioms to make the representation graphically clearer, but each diagram

captures the essential idea of the mentioned axiom.)

< A I B I C > is represented by a pair of labelled arrows with common domain:

(This treats symmetry, too.)

Decomposition and weak union axe done with factorisation:

Contraction is handled by composition:

Perhaps most curiously, intersection can be written as "one half" of the existence

of pull-backs (see e.g. [McL71J):

Thus, people who prefer to think graphically can use this representation.

One of the questions of the introduction is ;'answered" by the tbllowing complete-

ness conjecture reversing Theorem 6.50:

218 CHAPTER 6. STRUCTURED REASONING

Diagram 6.33

B

_

BUA

A

~BUC

Diagram 6.34

B

A

.BUCUD

BUC

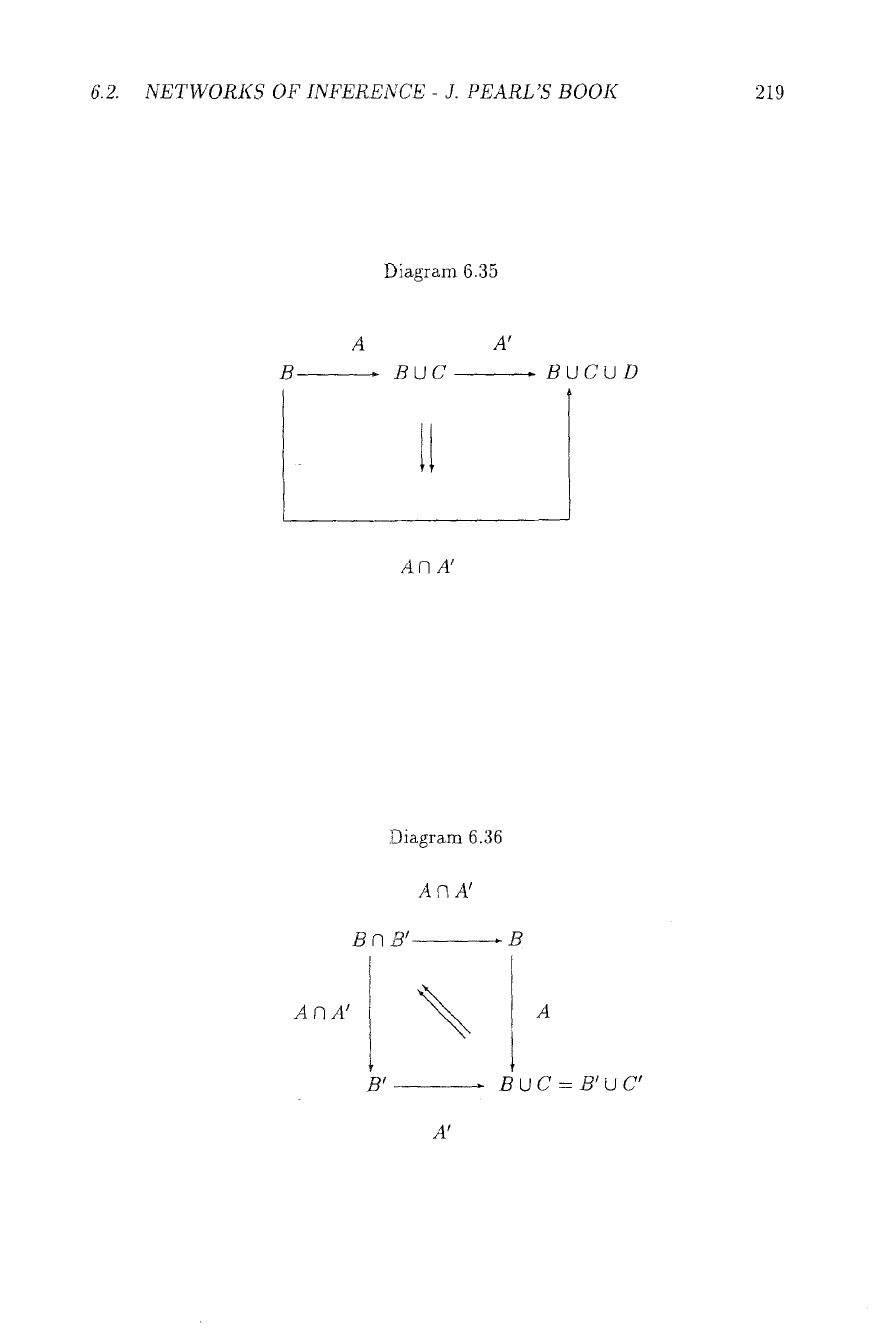
6.2. NETWORKS OF INFERENCE - J. PEARL'S BOOK 219

Diagram 6.35

A A'

B BUC BUCUD

Lt

AN A'

AAA'

Diagram 6.36

An A I

B r~ B I

~ B

\

B'

A'

A

,. BUC=WUC ~

220

CHAPTER 6. STRUCTURED REASONING

Completeness conjecture Axioms a)-d) in Theorem 6.50 characterize < . {

9 I. >P, axioms a)-e) there characterize < . [. I- >P for strictly positive P, i.e.

e.g. for a)-d): If K; is any set,/~ a a-place relation on T'(J~), and R satisfies a)-d),

then there is U and a probability measure

Pu

: P(II/J) --+ [0, 1] and a bijection

f: K ~/g such that < A[ B [ C >R ~ < f[A] ]

f[B]] f[C] >Pu.

Independence in undirected graphs (Sections 3.1.3 and 3.2 in Pearl's

book)

Let, in the sequel, F = (V, g) be an undirected graph with vertices V and edges

g.

Definition 6.51 a) Let X,Y be nodes in P. An uninterrupted sequence ~ of

edges, beginning in X, ending in Y is called a path from X to Y (or : X + Y). A

node Z is called on a, if it is at one end of one of c~'s edges. When no confusion

is possible, we denote by cr also the set of the nodes on it.

b) cr : X -+ Y is called a path from X to y (X,y C_ )j), iff X E X, Y E Y.

c) < X ] 32 ] Z >r :~ all pa.ths from X to Z have non-empty intersection with

y, i.e. go through 32. (2(, y, Z C l])

Note that < X ] 33 [ Z >r is monotone in the second argument. Consequently,

the third type of relevance described in the introduction - where the addition

of knowledge makes two formerly independent pieces of information dependent -

cannot be captured (at least not directly) by undirected graphs and the described

relation < 2( [ y{ Z >r.

Definition 6.52 Let R be a 3-place relation on "P(/C), F = (]2, $) an undirected

graph, and f : K: ~ V a bijection. Then

a) F is called a dependency map (D-map) of R iff < X [ Y I Z >R ~ <

fiX] l

fiX]

l f[Z]

>r for all X, 32,

Z C_

]C,

b) P is called an independency map @map) of R iff < X { 32 I Z >r --+ <

f-l[X] I f-l[Yl l.f-l[ Z]

>a for alt

X,y,Z C •,

c) r is called a perfect map of R iff < X ] Y ] Z >R ~ <

fiX] ] fiN] I f[Z]

>r

for alI X, 32, Z C/C,

d) R is called a graph-isomorph iff there is an undirected graph F, which is a

perfect map of R.

Theorem 6.53 Let R be a a-place relation on "P(lC), then R is a graph-isomorph

iff the following properties hold for R, i.e. graph-isomorphs are characterized by

the following five axioms:

a) Symmetry:

< X t ylZ >f~ ~ < Z

l YlX >R,

b) Decomposition: <XI32]ZtjW>R ~ <X IYlZ>R,

c) Intersection: < X I 3 )UW l g >R and < X [ 32UZ I W >n-+ < X I Y I

Z U 1/V >m

d) Strong Union: <KlYlZ>n--+<r

e) Transitivity: <X lYlZ>R~VTE/C (<XI3217>R~ <3'1YlZ>R)

(A' C ]C etc.).

6.2. NETWORKS OF INFERENCE - J. PEARL'S BOOK 221

F~

Diagram 6.37

M~

/

F~

/

The fact that probability measures might violate Axioms d) and e) above leads

to the definition of Markov Networks of R:

Definition 6.54 An undirected graph P is called a minima,1 I-map of R or a

Markov network of R, iff it is an independency map of R and deleting any edge

of F would destroy the I-map property, i.e. there would be X, y, Z _C 12 such

that < X l YIz >p, but not < f-l[X]lf-l[y][f-l[Z] >A.

We have

Theorem 6.55 If R is a a-place relation on T(K:), which satisfies a)-c) in The-

orem 6.53, then it has an (up to isomorphism) unique Markov network.

Moreover:

Theorem 6.56 For every undirected graph P there is a probability measure Pu

such that F is a perfect map of < . I- I. >P,.

Discussion and labelling of edges We give the following example, due to

Pearl [Pea88]

(3.1.3),

as illustration: "... consider a group of two males {M1, M2)

and two females {&, 4} who occasionally engage in pairwise heterosexual ac-

tivities. The lack of direct contact between the two males and between the two

females can be represented by ...":

"If we denote by m~ (or f~) the proposition that male -~L (or female ~) wilt

carry a certain disease within a year, then the topology of the network ... asserts

222 CHAPTER 0". STRUCTURED REASONING

that fl and f~ are independent given ml and ms, namely, once we know for sure

whether M1 and 342 will carry the disease, knowing the truth of fl ought not

change our belief in f2. This conditional independence reflects a model whereby

the disease spreads only by direct contact. Note that the links are undirected,

namely, either partner might be the originator of the disease. This does not

exclude asymmetric interactions (e.g. the disease may be more easily transferable

from males to females than the other way round). Such information ...will

be contained in the numerical parameters that eventually will characterize the

links in the network .... " These parameters are given by probability measures

PM,,F, : M~ x Fj --~ [0, 1]. Such probability measures are meaningful in the sense

that e.g. experts use and can provide them.

Pearl (in

3.2.a)

shortly describes a method ("Gibbs' potential") of finding such

(probabilistically) consistent and complete probability measures such that the

graph F will be an I-map of the resulfing (overall) probability measure.

Independence in directed acyclic graphs

Let A be a DAG, i.e. a directed, acyclic graph, assume further that each pair

X, Y of nodes is connected by at most one arrow. The following Definitions and

Facts are with respect to some fixed DAG 2x = ()2vertices, at. =arrows).

Definition 6.57 Let X,Y, Z etc. be in )2.

a) Path: If c~ = X --+ g or a = X +-- Y is in 2x, then cr is a path from X to Y;

we also write a = X...Y. If~ = X...Y is apath from X to !/, and Y ~ Z

(Y *-- Z) is in zX, then cr + (Y -+ Z) (c~ + (Y ~- Z)) is a path from X to Z, where

+ stands for concatenation.

b) Monotone path: ~r = X --+ Y --* ... -+ Z is a monotone path from X to Z.

We also say X > Z iff there is a monotone path from X to Z. By acyclicity, there

are no monotone paths cr : X --~ ... -+ X.

c) crc, cry: Let cr be a path, then a~ isthe set of nodes on or, where two arrows in

a converge, as is the set of other nodes on a. Example: If ~ = X -+ Y +-- Z, then

d) Parents, Children, Ancestors, Descendants: If X E )2, then

Gx := {Y E )2: Y --* X is in 2x} are the parents of X,

Cx := {Y E )2: X --~ Y is in A} are the children of X,

Ax := {Y E )2: there is a monotone path from Y to X} are the ancestors of X,

Ax := Ax u {X},

Dx := {Y E )2: there is a monotone path from X to Y} are the descendants of

X,

Dx := Dx U {X}.

e) Rank: rank(X) is the maximal length of the monotone paths leading into X.

(If Gx = ~, then rank(X) = 0.)

Definition 6.58 Let 2(, y, Z C 12.

6.2. NETWORKS OF INFERENCE - J. PEARL'S BOOK

223

a) A path r : X... Y is called Z-active iff Vu

E

~r~.D= M Z r • and ~r~ r3 Z = 0.

Otherwise, cr : X... Y is called blocked by Z. We also write cr : X... y iff there

isXEX, YEy, o:X...Y.

b) Set < X [ Z [ ~Y >a iff there is no X E X, Y E Y, cr : X...Y Z-active.

Note that <

X I

Z I Y >a is not any longer necessarily monotone in the second

argument. This enables to express the third type of relevance described in the

introduction.

Analogous to the situation in undirected graphs we define:

Definition 6.59 Let R be a 3-place relation on 7~(K), A = (V, A) a directed

graph, and f : K --+ 12 a bijection. Then

a) A is called a dependency map (D-map) of R iff < X I Y t Z >R -~ <

fix] I

f[Y]

[f[Z] >z~ for all X, y, Z c__/C.

b) A is called an independency map (I-map) of /~ iff < X [ y I Z >A --~

<

f-l[X][f-~[Y]lf-~[Z]

>R for all X,y,Z C 12.

c) z5 is called a perfect map of R iff < X [y [ Z >n H <

f[x]lf[y]l f[z] >A

for all X, Y, Z __ K.

d) R is called a directed graph isomorph (DAG isomorph) or causal iff there is

an directed graph A, which is a perfect map of R.

e) zX is called a minimal I-map of R, iff it is an independency map of R and

deleting any edge of A would destroy the I-map property, i.e. there would be

X,y,Z C_ 12

such that

< X ] y l Z

>a, but not <

f-~[X] ] f-~[Y] l f-~[Z] >_a.

If R is given by a probability measure

Pu,

then a minimal I-map A of R is also

called a Bayesian network of

Pu.

The following holds:

Theorem 6.60 a) Every probability measure Pu has a Bayesian network.

b) For every DAG A there exists a probability measure

Pu

such that A is a

perfect map of < . l-1" >Pu"

and

Theorem 6.61 Every DAG-isomorph R on 7)(K;) satisfies

a) Symmetry:

<

X

l YlZ >R H < z l YIX >R,

b)

Composition~Decomposition:

< X ] fl [ Z U 142 >R +-+ (< X I Y [ Z >R and

<XlYIW>R),

c) Intersection: (< X lYUI4J IZ >Rand < X I YUZ [ I42 >n)-~ < X [y]

ZUW

>]a,

d) WeakUnion: <XIYlZUW>R--~<XIyUld21Z>R,

e) Contraction: (< X [ y[ Z >R and < X I Y U Z [ W >n) + < X ] Y l

ZUW

>n,

f) Weak transitivity: (< X I Y ] Z >R and < ,t" I YU {7} ] Z >n)

(< x t YI7 >Rot <7

lYlZ

>~),

224

CHAPTER 6. STRUCTURED REASONING

g) Chordality: (< c~ f7,(51 /3 >R and < 7 i a,/3 I 6 >R) --~ (< c~ 17 I /3 >R or

(PC c_/C, c~ E JC etc.).

Before we go into the details of processing labelled DAG's, we comment the

situation.

Discussion The direction of arrows allows us to express causal relations. So the

(direct) arrow A --+ B expresses that A is considered a direct cause of B, or that

A has a direct influence on B. The relevance of the non-monotone independency-

relation has been mentioned already. The arrows - better the set of arrows going

into a node A - can be quantified in a natural and intuitive way by the conditional

probability

P[A I GA]

:=

{P(a

[g):a E

A,9

E Ha,,}. The reader should, how-

ever, also note some limitations in the expressiveness of DAG's: E.g., the example

discussed in the Section on undirected graphs cannot be faithfully described by a

DAG. (It is, however, possible to construct an "equivalent" DAG by introducing

an auxiliary node, say E. We then have < X I Y I Z >r iff < X I 32 ,E I Z >zx.

For details, see the end of Section 3.3.3 in [Pea88].) Moreover, not M1 depen-

dencies in probabilistic models can be exactly represented in DAG's. Again, the

reader is referred to [Pea88] for details.

6.2.3 Distributed computing in DAGs

([Pea88], Chapters 4,5.)

Fix now a finite DAG s = (1;,A). We first show 'that the information given

(as described in the prerequisite of Corollary 6.64) suffices to compute the joint

probability function. (This part is due to the present author.) We then go into the

details of Pearl's distributed computation by message passing in singly connected

DAGs. (This is- reshuffeled - material from [Pea88].)

Lemma 6.62 a) Let X, 3;, Z C_ Y. If there is a : X... y Z-active then there is

r : 2(... y such that r is a (by inclusion) minimal Z-active path between X and

y contained in a.

b) IfXEV, then<XtGx

lAx-Go; >~.

c) Let Xi E "P for i E I, and for i r j E I!et

Xi fL Dxj.

Set Yi :=

Ax,,

:= ~NU{Yj : i • j E [}, 23i := Yi-~, Zi := U{Yj : 3 E [}-Y~. Then

<Yil ~ t Zi >A. The result holds also if ~ = 0, i.e. then < Y~ II Zi >zx, thus in

particular if

rank(Xi) = O.

Proof a) Let X be the last node on r in X, Y the first node after X on cr in y,

and r the subpath of cr between X and Y. Clearly, r is a minimal path between

X and Y contained in cr. As a : X...Y was active, VU E ~rc.Dcr M Z ~ 0 and

or, M Z = ~. As r C ~r, this holds for r too, so r is active.

b) Assume there is a Gx-active from X to Y E

Ax - Gx. cr = X e- Z... Y

can't

be, as then Z E

Gx

M ~r~ . r can't be monotone, since otherwise there is a cycle

6.2. NETWORKS OF INFERENCE- d. PEARL'S BOOK

225

X ~ ... --+ Y --+ ... --+ X. So cr~ r 13, let Z be the first element of a~ on ~r. But

then c~ = X --~ ... --~ Z ~ ... ](" can't be active, since otherwise

Dz M Gx # 13,

and then there would be a cycle X --+ Z --+ ... -+ U E

Gx -+ X.

c) Disjointness is trivial. The special cases wit'h ~ = 13 follow from </2 I] 142 >A

iff for all ~r : U... W ~r~ # 13 - which has to hold by prerequisite. Assume there is

a ~-active path ~r : U... V for U EYi, V ~ Zi. By a), a can be assumed minimal

such. Let V E Yj, j # i. c~ = U --+ ... --+ V can't be monotone as then U E Yj.

Contradiction.

Case 1: cr = U ~ W... V, so W E Y, and W E ~ (by minimality of or), but then

W E ~r~ and ~r is not active.

Case 2: r = U ---+ W... V. We show by induction that r is monotone, and are

finished by above remark. Assume monotonicity holds up to R # IS, so ~r = U --+

W --+ ... --+ R .... V. By minimality of o', R r If R E Y//, then U E ~, as

is upward closed, but U E}~. So R r Y~, but then DR M ~ _C D--~ M Yi = !3.

As c~ is active, /~ r ~r~, so r = U --+ W--* ... + R--+ S...V. []

Let in the sequel P be a strictly positive probability measure on II)/(1; the vertices

of A), which satisfies the independency relations of A, i.e. if < 7t' [ 32 ] Z >A,

then

P(x I 9) = P(z ] y, z)

for x E FiX etc. (and likewise for y = ~3).

Lemma 6.63 Let

Xi : i E I, Xi E "1;

be such that for

i # j E I Xi f~ Dx,.

Then

P[U{Ax~:

i E I}] can be computed from {P A[~T] : i E I}, where P[X] := {<

z, P(x)

>: z E HA'} - i.e. the function P on the product IIA'.

Proof By induction on card(I). The case

card(I)

= 1 is trivial. Assume it has

been shown for all II such that

card(I1) < n,

let

card(I)

= n + 1, and i E I.

Assume the notation of Lemma 6.62, c), so <1~d ~ [ Z~ >a, and thus for

o

o o

P(Y, ~7, z) = e(y,~.P(z,~

But now Yi U~ = Y~ =

Ax,

and

p(~ "

P(f) = E{P(b, 9): b EII !~}, thus < b,~7 >E liE. By ~ U Z~ = U{)-xxj : i r E

I} and induction hypothesis,

P(z, ~1)

is computable from {P[AxTx,] : i 7 ~ j E I}.

(The case Y/= 13 is even simpler.) []

Corollary 6.64 Let A = (];, al) be a finite DAG as above. Let for each node

X ~ 1, ~ I(X) be given, where

I(X):= P[X] =:{<x,P(x)

>: x E X} if

Gx = 13,

and I(X) :=

P[X I ax]

= {<

x,y,P(x

I y) >: x E

X,y

E IICx} otherwise.

Let Z C_ p be a set of nodes in A, then

P[Z]

and P[U{Ay : Y E Z}] can be

computed from {I(X): X E A-Tv, Y E Z}.

In particular, if l) = {N~ ... N,~}, n~ E N,-, then all

P(nl ...

rim) can be computed

from all

I(Ni).

Thus, all "constants" etc. appearing in Pearl's algorithms can be

computed - when necessary - from the given information.

Proof By induction on p := maximal rank of elements in Z. p = 0: Then

no two ]I, YI E Z are comparable, and PlAY-y] = P[Y] is given by prerequisite.

Lemma 6.68 shows the result.

226 CHAPTER 6. STRUCTURED REASONING

p = n --+ p = n+l: Let ZI C_ Z be the set of <-minimal elements of Z (see

Definition 6.57, b). By Lemma 6.63, it suffices to show that all P[~zz], Z 9 Z I

can be computed from {I(X) : X E )T, Y E Z I}. Let Z E Z I. If rank(Z) <_ n,

P[~zz] can be computed from {I(X): X 9 A-zz} by induction hypothesis. So let

rank(Z) = n+l. If Az = Gz, then rank(Z) = 1, and for a 9 IIAz, z 9 Z we have

P(z, a) = P(z I a) * P(a). Otherwise, by Lemma 6.62, b) < Z I Gz I Az - Gz >,

so for z E Z, g 9 IIGz, a E II(Az - Gz), P(z,g,a) = P(z I g) * P(a,9). In

both cases, the former is given hy I(Z), and the latter can be computed from

{I(X) : X E Az} by induction hypothesis, as for X E Az, rank(X) < n. []

Assume now zi

to

be singly connected, i.e. for X,Y E 12 there is at most one

path cr connecting them.

Let E = {E~...E~} C_ y, e~ 9 E~, e = {e~... e~}. We now discuss the distributed

computation of P(x I e) for any x E X E V. The.computation rests heavily on the

single connectedness assumption. In intuitive terms, we are given the information

e, and are interested in the probability that z holds under this assumption.

Definition 6.65 Let X --~ Y be in zi. We define:

e~ := the information accessible from X via its children,

e~ := the information accessible from X via its parents,

Cxy := the information accessible from X not via Y,

eJ~ z := the information accessible from Y not via X,

where "accessible" means that there is a path to it. (s stands for source, d for

destination.)

(Pearl uses the notation e x := e~, e + := e~., exr := e~( z, e+v :: e~rz. ) Note

that d

c

[exvlv = e$ by e$ C_ e~: z. Ex c etc. is defined likewise, e.g. Ex c := {E~ 9

E : El accessible from X via its children },

As a picture:

Recollect that < X I Z I 3; >a:~ for all ~r : X...Y ( ~s N Z r (~ or there is

U E crc.Du M Z = ~ ). In particular, < X I[ Y >a ~ for all ~r : X...Y ~ro r (~.

Fact 6.66 The following are direct consequences of single connectedness:

a) <E~ I xlE~

>,

d ,'-

b) <Exz :Y E Clx X !E}v :Y E Crlx > for CtxNCItx =t~, CIx, CIIx ~

Cx,

c) < E)y : X E Glz II E)z : X E GIIy > for Gfv n GItz = (~, GIy,GIIy c Gy.

Definition 6.67 We use the following notation:

a~c := {z c cx : Ef.x = ~,v r E}, c~. := {v 9 cx : z~. r ~,v ~ E},

G}:={Y~Gx:YEE} and

c• := {z 9 cx : E}y : r r E), c1. ::,{z e cx : z}y r ~,v r E},

C} := {Y 9 Cx :Y E E}

Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques

Подождите немного. Документ загружается.