Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

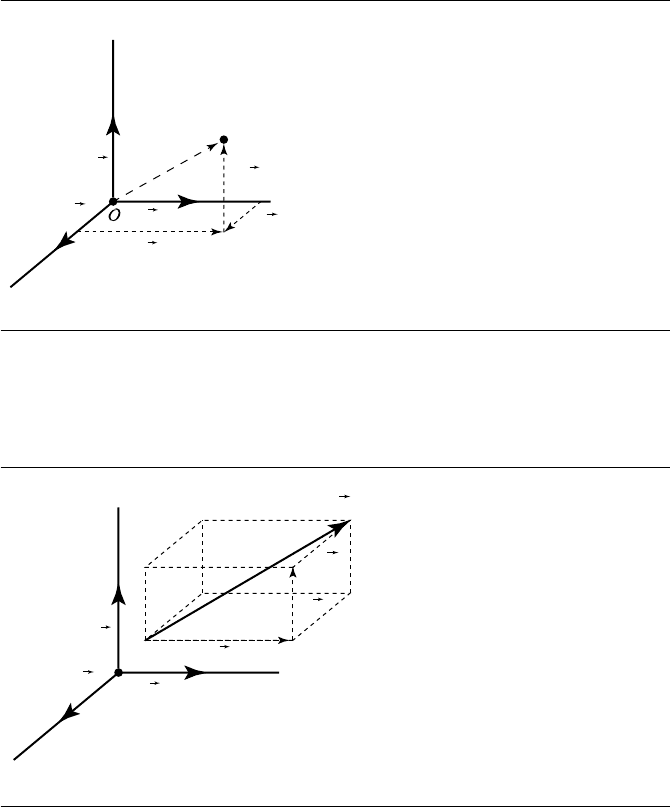
114 Chapter 4 Matrices, Vector Algebra, and Transformations
x
y
z
i
k
j
P = (p
1
, p
2
, p
3
)
p
1
i
p
2
j
p
3
k
Figure 4.1 P = p
1
ı +p
2
+ p
3
k + O = [p
1
p
2
p
3
1].
x
y
z
i
k
j
v
1
i
v
2
j
v
3
k
v = (v
1
, v
2
, v
3
)
Figure 4.2 v =v
1
ı +v
2
+ v
3
k = [v
1
v
2
v
3
0].
4.3.2 Point and Vector Addition and Subtraction
Adding or subtracting a point and vector is similar to vector/vector addition and
subtraction: Suppose we have a point P = p
1
ı + p
2
+ p
3
k + O and vector v =
v
1
ı +v
2
+ v
3
k. To add their matrix representations:
4.4 Products of Vectors 115
P +v =
[
p
1
p
2
p
3
1
]
+
[
v
1
v
2
v
3
0
]
= p
1
ı +p
2
+ p
3
k + O + v
1
ı +v
2
+ v
3
k
= (p
1
+ v
1
)ı + (p
2
+ v
2
) + (p
3
+ v
3
)
k + O
=
[
p
1
+ v
1
p
2
+ v
2
p
3
+ v
3
1
]
Again the proof for subtraction is similar.
4.3.3 Subtraction of Points
Suppose we have two points P = p
1
ı +p
2
+ p
3
k + O and Q = q
1
ı +q
2
+ q
3
k +
O, and we wish to subtract them in their matrix representations:
P − Q =
[
p
1
p
2
p
3
1
]
−
[
q
1
q
2
q
3
1
]
= (p
1
ı +p
2
+ p
3
k + O) − (q
1
ı +q
2
+ q
3
k + O)
= (p
1
− q
1
)ı + (p
2
− q
2
) + (p
3
− q
3
)
k
=
[
p
1
− q
1
p
2
− q
2
p
3
− q
3
0
]
4.3.4 Scalar Multiplication
Suppose we have a vector v = v
1
ı +v
2
+ v
3
k, which we wish to multiply by a scalar
α. In terms of the matrix representation we have
αv =α
[
v
1
v
2
v
3
0
]
= α(v
1
ı +v
2
+ v
3
k)
= (αv
1
)ı + (αv
2
) + (αv
3
)
k
=
[
αv
1
αv
2
αv
3
0
]
(4.6)
4.4 Products of Vectors
While the preceding proofs of addition, subtraction, and multiplication were trivial
and obvious, we’ll see in the following sections that the approach taken will be of great
benefit in assisting our understanding of the componentwise operations involved
in the computation of the dot and cross products. Generally, texts discussing these
operations simply present the formula; our intention is to show why these operations
work.
116 Chapter 4 Matrices, Vector Algebra, and Transformations
4.4.1 Dot Product
In Section 3.3.1, we discussed the scalar (or dot) product of two vectors as an abstract,
coordinate-free operation. We also discussed, in Section 2.3.4, an inner (specifically,
the dot)productofa1× n matrix (“row vector”) and an n × 1 matrix (“column
vector”). The perceptive reader may have noted that both of these operations were
called the dot product, and of course this is no coincidence. Specifically, we have
u ·v =
[
u
1
u
2
··· u
n
]
v
1
v
2
.
.
.
v
n
That is, the scalar/dot product of two vectors is represented in terms of matrix oper-
ations as the inner/dot product of their matrix representations.
Of course, the interesting point here is why this is so; it’s not directly obvious why
multiplying the individual coordinate components, and then summing them, yields a
value related to the angle between the vectors. To understand this, it’s better to go the
other direction: assume the coordinate-free definition of the dot product, and then
show how this leads to the matrix inner product. The approach is again similar to
that used to prove addition and subtraction of points and vectors.
Suppose we have two vectors u and v. By definition their dot product is
u ·v =uvcos θ
If we apply this definition to the basis vectors, we get
ı ·ı =ıı cos θ = 1 · 1 · 1 = 1
· = cos θ = 1 · 1 · 1 =1
k ·
k =
k
k cos θ = 1 · 1 · 1 = 1
because the angle between any vector and itself is 0, whose cosine is 1.
Applying the dot product defintion to the basis vectors pairwise yields
ı · =ı cos θ = 1 · 1 · 0 =0
ı ·
k =ı
k cos θ = 1 · 1 · 0 =0
·
k =
k cos θ = 1 · 1 · 0 =0
because the basis vectors are of unit length, and the angle between them is π/2, whose
cosine is 0.

4.4 Products of Vectors 117
If we have vectors u =u
1
ı +u
2
+u
3
k and v =v
1
ı +v
2
+v
3
k, we can compute
their dot product as
u ·v =
[
u
1
u
2
u
3
0
]
·
[
v
1
v
2
v
3
0
]
= (u
1
ı +u
2
+ u
3
k) · (v
1
ı +v
2
+ v
3
k)
= u
1
v
1
(ı ·ı) + u
1
v
2
(ı ·)+ u
1
v
3
(ı ·
k)
+ u
2
v
1
( ·ı) + u
2
v
2
( ·)+ u
2
v
3
( ·
k)
+ u
3
v
1
(
k ·ı) + u
3
v
2
(
k ·) + u
3
v
3
(
k ·
k)
= u
1
v
1
+ u
2
v
2
+ u
3
v
3
4.4.2 Cross Product
While the matrix representation of the dot product was almost painfully obvious,
the same cannot be said for the cross product. The definition for the cross product
(see Section 3.3.1) is relatively straightforward, but it wasn’t given in terms of a single
matrix operation; that is, if we see an expression like
w =u ×v (4.7)
how do we implement this in terms of matrix arithmetic?
There are actually two ways of dealing with this:
If we simply want to compute a cross product itself, how do we do so directly?
Can we construct a matrix that can be used to compute a cross product? If we
have a sequence of operations involving dot products, cross products, scaling, and
so on, then such a matrix would allow us to implement them consistently—as a
sequence of matrix operations.
We’ll deal with both of these approaches, in that order.
Direct Cross Product Computation
As with the discussion of the dot product, we start by recalling the definition of the
cross product: if we have two vectors u = u
1
ı +u
2
+ u
3
k and v = v
1
ı +v
2
+ v
3
k,
their cross product is defined by three properties:
118 Chapter 4 Matrices, Vector Algebra, and Transformations
i. Length:
u ×v=uv| sin θ |
If we apply this to each of the basis vectors we have the following:
ı ×ı =
0
× =
0
k ×
k =
0
because the angle between any basis vector and itself is 0, and the sine of 0 is 0.
ii. Orthogonality:
u ×v ⊥u
u ×v ⊥v
iii. Orientation: The right-hand rule determines the direction of the cross product
(see Section 3.2.4). This, together with the second property, can be applied to the
basis vectors to yield the following:
ı × =
k
×ı =−
k
×
k =ı
k × =−ı
k ×ı =
ı ×
k =−
because the basis vectors are mutually perpendicular and follow the (arbitrarily
chosen) right-hand rule.
4.4 Products of Vectors 119
With all of this in hand, we can now go on to prove the formula for the cross product:
u ×v =
[
u
1
u
2
u
3
0
]
×
[
v
1
v
2
v
3
0
]
= (u
1
ı +u
2
+ u
3
k) × (v
1
ı +v
2
+ v
3
k)
= (u
1
v
1
)(ı ×ı) + (u
1
v
2
)(ı ×)+ (u
1
v
3
)(ı ×
k)
+ (u
2
v
1
)( ×ı) + (u
2
v
2
)( ×)+ (u
2
v
3
)( ×
k)
+ (u
3
v
1
)(
k ×ı) + (u
3
v
2
)(
k ×) + (u
3
v
3
)(
k ×
k)
= (u
1
v
1
)
0 +(u
1
v
2
)
k + (u
1
v
3
)(−)
+ (u
2
v
1
)(−
k) + (u
2
v
2
)
0 +(u
2
v
3
)ı
+ (u
3
v
1
) + (u
3
v
2
)(−ı) + (u
3
v
3
)
0
= (u
2
v
3
− u
3
v
2
)ı + (u
3
v
1
− u
1
v
3
) + (u
1
v
2
− u
2
v
1
)
k +
0
=
[
u
2
v
3
− u
3
v
2
u
3
v
1
− u
1
v
3
u
1
v
2
− u
2
v
1
0
]
Cross Product as Matrix Multiplication
Perhaps it would be best to show an example and then go on to why this works. Given
an expression like Equation 4.7, we’d like to look at it in this way:
w =u ×v
=
[
u
1
u
2
u
3
]
?
Recall that the definition of cross product is
w =u ×v
=
u
2
v
3
− u
3
v
2
, u
3
v
1
− u
1
v
3
, u
1
v
2
− u
2
v
1
Using the definition of matrix multiplication, we can then reverse-engineer the de-
sired matrix, a “skew symmetric matrix,” and we use the notation ˜v:
˜v =
0 −v
3
v
2
v
3
0 −v
1
−v
2
v
1
0
120 Chapter 4 Matrices, Vector Algebra, and Transformations
Taking all this together, we get
w =u ×v
=
[
u
1
u
2
u
3
]
˜v
=
[
u
1
u
2
u
3
]
0 −v
3
v
2
v
3
0 −v
1
−v
2
v
1
0
Depending on the context of the computations, we might wish to instead reverse
which vector is represented by a matrix. Because the cross product is not commuta-
tive, we can’t simply take ˜v and replace the vs with us. Recall, however, that the cross
product is antisymmetric
u ×v =−(v ×u)
and recall that in Section 2.3.4, we showed that we could reverse the order of matrix
multiplication by transposing the matrices.
Thus, if we want to compute w =v ×u (with, as before, u retaining its usual
matrix representation), we have
˜v =
0 v
3
−v
2
−v
3
0 v
1
v
2
−v
1
0
resulting in
w =v ×u
=˜v u
w
1
w
2
w
3
=
0 v
3
−v
2
−v
3
0 v
1
v
2
−v
1
0
u
1
u
2
u
3
4.4.3 Tensor Product
Another common expression that arises in vector algebra is of this form:
t =
u ·v
w (4.8)
We’d like to express this in terms of matrix arithmetic on u, in order to have opera-
tions of the form
4.4 Products of Vectors 121
[
t
1
t
2
t
3
]
=
[
u
1
u
2
u
3
][
?
]
Recall from Section 4.4.1 the definition of a dot product (yielding a scalar), and
from Section 4.3.4 the definition of multiplication of a vector by a scalar (yielding
a vector). We can use these to reverse-engineer the needed matrix, which is a tensor
product of two vectors and is noted as v ⊗w, and so we have
t =
u ·v
w
=
[
u
1
u
2
u
3
]
v
1
w
1
v
1
w
2
v
1
w
3
v
2
w
1
v
2
w
2
v
2
w
3
v
3
w
1
v
3
w
2
v
3
w
3
If you multiply this out, you’ll see that the operations are, indeed, the same as those
specified in Equation 4.8. This also reveals the nature of this operation; it transforms
the vector u into one that is parallel to w:
t =
[
(u
1
v
1
+ u
2
v
2
+ u
3
v
3
)w
1
(u
1
v
1
+ u
2
v
2
+ u
3
v
3
)w
2
(u
1
v
1
+ u
2
v
2
+ u
3
v
3
)w
3
]
This operation is a linear transformation of u for the two vectors v and w because
it transforms vectors to vectors and preserves linear combinations; its usefulness will
be seen in Section 4.7. It is also important to note that the order of the vectors is
important: generally, ( w ⊗v)
T
=v ⊗w.
4.4.4 The “Perp” Operator and the “Perp” Dot Product
The perp dot product is a surprisingly useful, but perhaps underused, operation on
vectors. In this section, we describe the perp operator and its properties and then go
on to show how this can be used to define the perp dot operation and describe its
properties.
The Perp Operator
We made use of the ⊥ (pronounced “perp”) operator earlier, without much in the
way of explanation. If we have a vector v, then v
⊥
is a vector perpendicular to it (see
Figure 4.3). Of course, in 2D there are actually two perpendicular vectors (of the same
length), one at 90
◦
clockwise and one at 90
◦
counterclockwise. However, since we
have adopted a right-handed convention, it makes sense to choose the perpendicular
vector 90
◦
counterclockwise, as shown in the figure.
Perpendicular vectors arise frequently in 2D geometry algorithms, and so it
makes sense to adopt this convenient notation. In terms of vectors, the operation
is intuitive and rather obvious. But what about the matrix representation? The vector

122 Chapter 4 Matrices, Vector Algebra, and Transformations
v
v
Figure 4.3 The“perp”operator.
v in Figure 4.3 is approximately [
1 0.2
]. Intuitively, the “trick” is to exchange the
vector’s two components and then negate the first. In matrix terms, we have
v
⊥
=
[
1 0.2
]
01
−10
=
[
−0.2 1
]
In 3D, there are an infinite number of vectors that are perpendicular to, and the
same length as, a given vector (defining a “disk” perpendicular to the vector). It is not
possible to define a consistent rule for forming a unique, distinguished “perp” in 3D
for all vectors, which seems to limit the applicability of the perp operator for 3D; we
therefore concentrate on 2D for the remainder of the discussion.
Properties
Hill (1994) gives us some useful properties of the perp operator:
i. v
⊥
⊥v.
ii. Linearity:
a. (u +v)
⊥
=u
⊥
+v
⊥
.
b. (k v)
⊥
= k(v
⊥
), ∀k ∈ R.
iii. v
⊥
=v.
iv. v
⊥⊥
= (v
⊥
)
⊥
=−v.
v. v
⊥
is 90
◦
counterclockwise rotation from v.
Proof i. v
⊥
·v =[
−v
y
v
x
]·
[
v
x
v
y
]
=−v
y
· v
x
+ v
x
· v
y
= 0. Since the dot product
is zero, the two vectors are perpendicular.

4.4 Products of Vectors 123
ii. a.
(u +v)
⊥
=u
⊥
+v
⊥
(
[
u
x
u
y
]
+
[
v
x
v
y
]
)
⊥
=
[
−u
y
u
x
]
+
[
−v
y
v
x
]
[
u
x
+ v
x
u
y
+ v
y
]
⊥
=
[
−(u
y
+ v
y
)u
x
+ v
x
]
[
−(u
y
+ v
y
)u
x
+ v
x
]
=
[
−(u
y
+ v
y
)u
x
+ v
x
]
b.
(kv)
⊥
= k(v
⊥
)
(k
[
v
x
v
y
]
)
⊥
= k
[
v
x
v
y
]
⊥
[
kv
x
kv
y
]
⊥
= k
[
−v
y
v
x
]
[
−kv
y
kv
x
]
=
[
−kv
y
kv
x
]
iii.
(−v
y
)
2
+ (v
x
)
2
=
(v
x
)
2
+ (v
y
)
2
iv.
v
⊥⊥
= (v
⊥
)
⊥
=−v
[
v
x
v
y
]
⊥⊥
= (
[
v
x
v
y
]
⊥
)
⊥
=−
[
v
x
v
y
]
[
−v
y
v
x
]
⊥
=
[
−v
y
v
x
]
⊥
=
[
−v
x
−v
y
]
[
−v
x
−v
y
]
=
[
−v
x
−v
y
]
=
[
−v
x
−v
y
]
v. If we have a complex number x
a
+ y
a
· i and multiply it by the complex number
i, we get a complex number that is 90
◦
counterclockwise from a: −y
a
+ x
a
· i.A
vector v can be considered to be the point v
x
+ v
y
· i in the complex plane, and
v
⊥
can be considered to be the point −v
y
+ v
x
· i.
The Perp Dot Operation
Hill’s excellent article provides a variety of applications of the perp dot operation,
and you are encouraged to study them in order to understand how widely useful that
operation is. So, here we will be content just to briefly summarize the operation and
its significance.
The perp dot operation is simply the application of the usual dot product of two
vectors, the first of which has been “perped”: u
⊥
·v. Before identifying and proving
various properties of the perp dot product, let’s analyze its geometric properties.
Geometric Interpretation
There are two important geometrical properties to consider. Let’s first recall the
relationship of the standard dot product of two vectors to the angle between them.
Given two vectors u and v,wehave
