Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

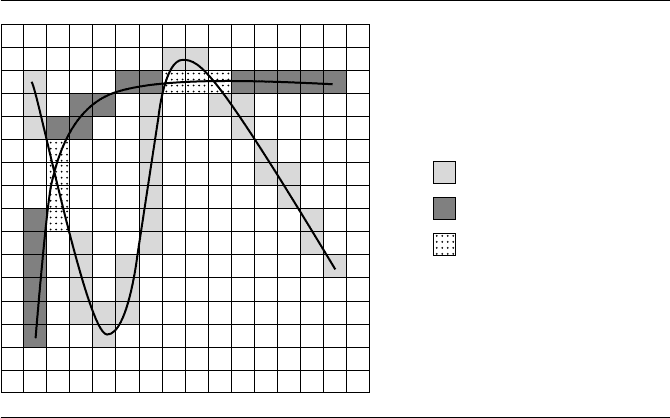
264 Chapter 7 Intersection in 2D
Contains curve 1
Contains curve 2
Contains both
Figure 7.11 Two curves rasterized on a grid that is initially zero. The first curve is rasterized by
or-ing the grid with the mask 1 (light gray). The second curve is rasterized by or-ing
the grid with the mask 2 (dark gray). Grid cells that contain both curves have a value
3 (dotted).
or-ing the pixels with 2, the pixels that are associated with curve-curve intersections
are those with a final value of 3 (see Figure 7.11).
Notice that the leftmost block of pixels (dotted cells) make it uncertain where the
curves might intersect, if at all. The problem generally is that two curves can be near
each other, yet not intersect, and be rasterized into the same pixels. The solution is to
increase the number of cells while reducing the cell size to get a finer-resolution grid.
How small a cell size should be to properly detect intersections and not produce false
positives is usually information that is not known ahead of time.
Just as in the polyline approach, the application can choose to accept the pixel
values as approximations to the actual curve-curve intersections. If more accuracy is
desired, the pixels tagged as 3 (and possibly immediate neighbors) can be used as a
localization of where the intersections occur. If a contiguous block of pixels is tagged,
such as is shown in the left of the grid in Figure 7.11, and if the application chooses
to believe the block occurs because of a single intersection of curves, a suitable choice
for the approximation is the average of pixel locations. If the application chooses
not to accept the pixel values as approximations, then it can store the original curve
parameters for samples occurring in a pixel with that pixel. Those parameter values
can be used to start a search for intersections using a numerical root finder or a
numerical distance calculator.
7.7 The Method of Separating Axes 265
7.7 The Method of Separating Axes
AsetS is convex if given any two points P and Q in S, the line segment (1−t)P +tQ
for t ∈[0, 1]is also in S. This section describes the method of separating axes in 2D—a
method for determining whether or not two stationary convex objects are intersect-
ing. The ideas extend to moving convex objects and are useful for predicting collisions
of the objects by computing the first time of contact and for computing the contact
set. Two types of geometric queries are considered. The first is a test-intersection query
that just indicates whether or not an intersection exists for stationary objects or will
occur for moving objects. The second is a find-intersections query that involves com-
puting the set of intersections for two stationary objects or for two moving objects
at the time of first contact. This section describes both types of queries for convex
polygons in 2D.
The following notation is used throughout this section. Let C
j
for j = 0, 1 be
the convex polygons with vertices {V
(j)
i
}
N
j
−1
i=0
that are counterclockwise ordered.
The edges of the polygons are e
(j)
i
= V
(j)
i+1
− V
(j)
i
for 0 ≤ i<N
j
and where V
(j)
N
j
=
V
(j)
0
. Outward pointing normal vectors to the edges are
d
(j)
i
= Perp
e
(j)
i
,where
Perp(x, y) = (y, −x).
7.7.1 Separation by Projection onto a Line
A test for nonintersection of two convex objects is simply stated: if there exists a
line for which the intervals of projection of the two objects onto that line do not
intersect, then the objects do not intersect. Such a line is called a separating line or,
more commonly, a separating axis (see Figure 7.12). The translation of a separating
line is also a separating line, so it is sufficient to consider lines that contain the origin.
Given a line containing the origin and with unit-length direction
d, the projection of
aconvexsetC onto the line is the interval
I = [λ
min
(
d), λ
max
(
d)] = [min{
d ·
X :
X ∈ C}, max{
d ·
X :
X ∈ C}]
where possibly λ
min
(
d) =−∞or λ
max
(
d) =+∞; these cases arise when the convex
set is unbounded. Two convex sets C
0
and C
1
are separated if there exists a direction
d such that the projection intervals I
0
and I
1
do not intersect. Specifically they do not
intersect when
λ
(0)
min
(
d)>λ
(1)
max
(
d) or λ
(0)
max
(
d)<λ
(1)
min
(
d) (7.10)
The superscript corresponds to the index of the convex set. Although the compar-
isons are made where
d is unit length, the comparison results are invariant to changes
in length of the vector. This follows from λ
min
(t
d) = tλ
min
(
d) and λ
max
(t
d) =
tλ
max
(
d) for t>0. The Boolean value of the pair of comparisons is also invariant
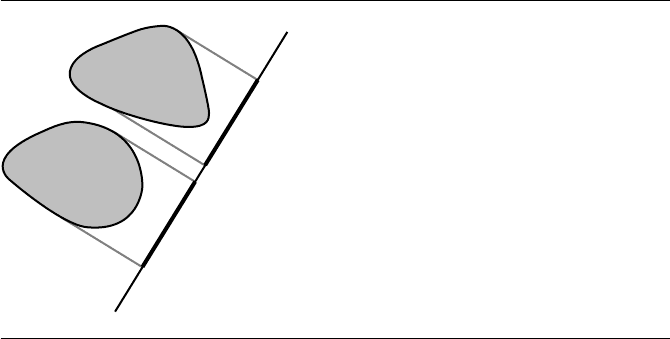
266 Chapter 7 Intersection in 2D
Figure 7.12 Nonintersecting convex objects and a separating line for them.
when
d is replaced by the opposite direction −
d.Thisfollowsfromλ
min
(−
d) =
−λ
max
(
d) and λ
max
(−
d) =−λ
min
(
d). When
d is not unit length, the intervals ob-
tained for the separating line tests are not the projections of the object onto the line;
rather they are scaled versions of the projection intervals. We make no distinction
between the scaled projection and regular projection. We will also use the terminol-
ogy that the direction vector for a separating line is called a separating direction,a
direction that is not necessarily unit length.
Please note that in two dimensions, the terminology for separating line or axis
is potentially confusing. The separating line separates the projections of the objects
on that line. The separating line does not partition the plane into two regions, each
containing an object. In three dimensions, the terminology should not be confusing
since a plane would need to be specified to partition space into two regions, each
containing an object. No real sense can be made for partitioning space by a line.
7.7.2 Separation of Stationary Convex Polygons
For a pair of convex polygons, only a finite set S of direction vectors needs to be
considered for separation tests. That set contains only the normal vectors to the
edges of the polygons. Figure 7.13(a) shows two nonintersecting polygons that are
separated along a direction determined by the normal to an edge of one polygon.
Figure 7.13(b) shows two polygons that intersect; there are no separating directions.
The intuition for why only edge normals must be tested is based on having two
convex polygons just touching with no interpenetration. Figure 7.14 shows the three
possible configurations: edge-edge contact, vertex-edge contact, and vertex-vertex
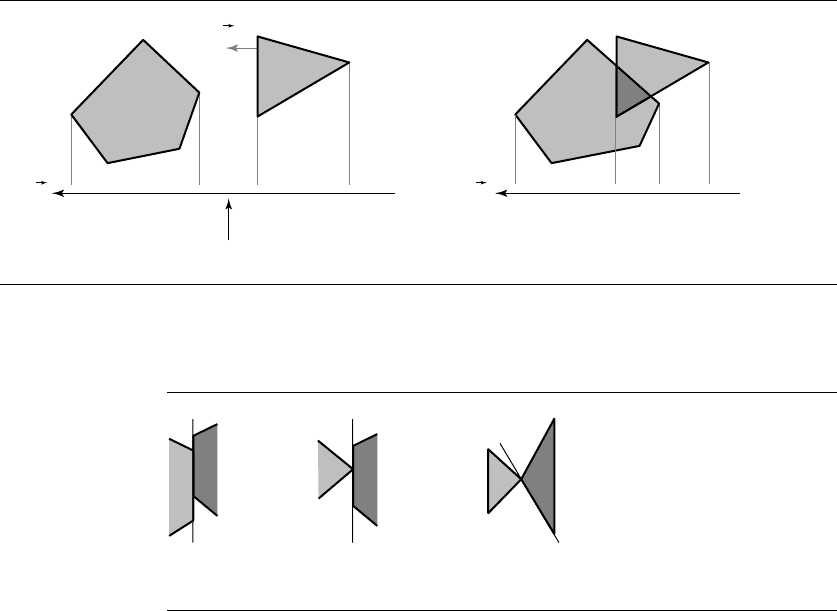
7.7 The Method of Separating Axes 267
[
[
[
[
d
[[
[[
Projection(C
0
) No separation on any axisProjection(C
1
)
Separation
(a) (b)
C
0
C
1
C
0
C
1
d
d
Figure 7.13 (a) Nonintersecting convex polygons. (b) Intersecting convex polygons.
(a) (b) (c)
Figure 7.14 (a) Edge-edge contact, (b) vertex-edge contact, and (c) vertex-vertex contact.
contact. The lines between the polygons are perpendicular to the separation lines
that would occur for one object translated away from the other by an infinitesimal
distance.
The mathematical proof that S contains only edge normals is based on showing
that if
d is a separating direction that is not normal to an edge of either convex
polygon, then there must be an edge normal that is also a separating direction. Let
d = (cos θ, sin θ) be a separating direction that is not normal to an edge. For the
sake of argument, assume that the projection of C
0
onto the separating line is on
the left of the projection of C
1
. A similar argument directly applies if it were on the
right. Since
d is not an edge normal, only one vertex V
0
of C
0
maps to λ
(0)
max
, and only
one vertex V
1
of C
1
maps to λ
(1)
min
.Letθ
0
be the largest angle smaller than θ so that
d
0
=(cos θ
0
, sin θ
0
) is an edge normal, but
d(φ)=(cos φ, sin φ) is not an edge normal
for all φ ∈ (θ
0
, θ]. Similarly, let θ
1
be the smallest angle larger than θ so that
d
1
=
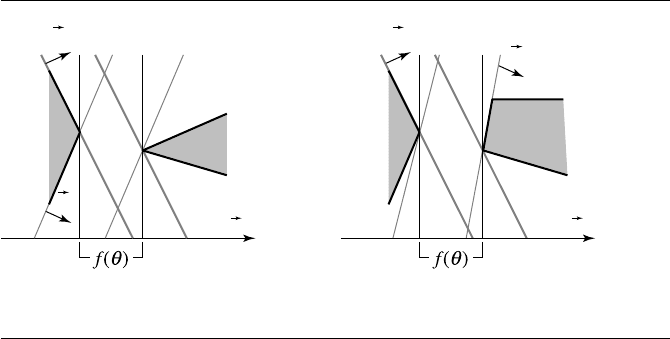
268 Chapter 7 Intersection in 2D
(a) (b)
d
0
d
0
d d
d
1
d
1
Figure 7.15 The edge normals closest to a non-edge-normal separation direction: (a) from the
same triangle and (b) from different triangles.
(cos θ
1
, sin θ
1
) is an edge normal, but
d(φ) is not an edge normal for all φ ∈ [θ, θ
1
).
For all directions
d(φ) with φ ∈ (θ
0
, θ
1
), V
0
is the unique vertex that maps to λ
(0)
max
and V
1
is the unique vertex that maps to λ
(1)
min
. The separation between the intervals
is the continuous function f(φ)=(cos φ, sin φ) · (V
1
−V
0
) =A cos(φ +ψ),where
A is a constant amplitude and ψ is a constant phase angle. Also, f(θ)>0 since
d is
a separating direction.
If f(θ
0
)>0, then the edge normal
d
0
is also a separating direction. If f(θ
1
)>0,
then the edge normal
d
1
is also a separating direction. Suppose that f(θ
0
) ≤ 0 and
f(θ
1
) ≤ 0. Since f(θ)>0, there must exist two zeros of f on [θ
0
, θ
1
], one smaller
than θ and one larger than θ.Thezerosoff are separated by π radians. This forces
θ
1
−θ
0
≥π, in which case the angle between the consecutive edge normals
d
0
and
d
1
is at least π radians. This happens only if the angle is exactly π , the two edges sharing
V
0
are parallel to
d, and the two edges sharing V
1
are parallel to
d, a contradiction to
the angles at those vertices being strictly positive. Therefore, it is impossible that both
f(θ
0
) ≤ 0 and f(θ
1
) ≤ 0. In summary, if f(θ)>0, then either f(θ
0
)>0, in which
case
d
0
is a separating edge normal, or f(θ
1
)>0, in which case
d
1
is a separating edge
normal.
Figure 7.15 illustrates what
d
0
and
d
1
mean. Figure 7.15(a) shows the case where
both nearest edge normals are from the same triangle. Figure 7.15(b) shows the case
where the nearest edge normals are from different triangles.
7.7 The Method of Separating Axes 269
The Direct Implementation
The direct implementation for a separation test for direction
d just computes the
extreme values of the projection and compares them. That is, compute λ
(j)
min
(
d) =
min
0≤i<N
0
{
d · V
(j)
i
} and λ
(j)
max
(
d) = max
0≤i<N
1
{
d · V
(j)
i
} and test the inequalities in
Equation 7.10. The pseudocode is listed below.
bool TestIntersection(ConvexPolygon C0, ConvexPolygon C1)
{
// test edge normals of C0 for separation
for (i0 = 0, i1 = C0.N-1; i0 < C0.N; i1 = i0, i0++) {
D = Perp(C0.E(i1)); // C0.E(i1) = C0.V(i0) - C0.V(i1)
ComputeInterval(C0, D, min0, max0);
ComputeInterval(C1, D, min1, max1);
if (max1 < min0 || max0 < min1)
return false;
}
// test edge normals of C1 for separation
for (i0 = 0, i1 = C1.N - 1; i0 < C1.N; i1 = i0, i0++) {
D = Perp(C1.E(i1)); // C1.E(i1) = C1.V(i0) - C1.V(i1));
ComputeInterval(C0, D, min0, max0);
ComputeInterval(C1, D, min1, max1);
if (max1 < min0 || max0 < min1)
return false;
}
return true;
}
void ComputeInterval(ConvexPolygon C, Point D, float& min, float& max)
{
min = max = Dot(D, C.V(0));
for (i = 1; i < C.N; i++) {
value = Dot(D, C.V(i));
if (value < min)
min = value;
else if (value > max)
max = value;
}
}
270 Chapter 7 Intersection in 2D
[[]]
0
d
d
Figure 7.16 Two polygons separated by an edge-normal direction of the first polygon.
Observe that the implementation always processes potential separating lines that
contain the origin. When polygons are relatively far from the origin, a variation on the
implementation to deal with floating-point errors would involve choosing a potential
separating line that contains a polygon vertex, thereby hoping to keep intermediate
floating-point values relatively small.
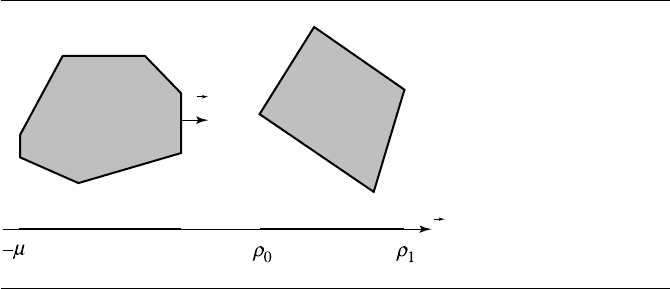
An Alternative Implementation
An alternative algorithm avoids projecting all the vertices for the polygons by only
testing for separation using the maximum of the interval for the first polygon and
the minimum of the interval for the second polygon. If
d is an outward pointing
normal for the edge V
i+1
− V
i
of the first polygon, then the projection of the first
polygon onto the separating line V
i
+ t
d is [−µ,0],whereµ>0. If the projection
of the second polygon onto this line is [ρ
0
, ρ
1
], then the reduced separation test is
ρ
0
> 0. Figure 7.16 illustrates two separated polygons using this scheme. The value µ
is irrelevant since we only need to compare ρ
0
to 0. Consequently, there is no need to
project the vertices of the first polygon to calculate µ. Moreover, the vertices of the
second polygon are projected one at a time until either the projected value is negative,
in which case
d is no longer considered for separation, or until all projected values are
positive, in which case
d is a separating direction.
bool TestIntersection(ConvexPolygon C0, ConvexPolygon C1)
{
// Test edges of C0 for separation. Because of the counterclockwise ordering,
// the projection interval for C0 is [m,0] where m <= 0. Only try to determine
// if C1 is on the ‘positive’ side of the line.
7.7 The Method of Separating Axes 271
for (i0 = 0, i1 = C0.N - 1; i0 < C0.N; i1 = i0, i0++) {
D = Perp(C0.E(i1)); // C0.E(i1) = C0.V(i0) - C0.V(i1));
if (WhichSide(C1.V, C0.V(i0), D) > 0) {
// C1 is entirely on ‘positive’ side of line C0.V(i0)+t*D
return false;
}
}
// Test edges of C1 for separation. Because of the counterclockwise ordering,
// the projection interval for C1 is [m,0] where m <= 0. Only try to determine
// if C0 is on the ‘positive’ side of the line.
for (i0 = 0, i1 = C1.N - 1; i0 < C1.N; i1 = i0, i0++) {
D = Perp(C1.E(i1)); // C1.E(i1) = C1.V(i0) - C1.V(i1));
if (WhichSide(C0.V, C1.V(i0), D) > 0) {
// C0 is entirely on ‘positive’ side of line C1.V(i0)+t*D
return false;
}
}
return true;
}
int WhichSide(PointSet S, Point P, Point D)
{
// S vertices are projected to the formP+t*D. Return value is +1 if allt>0,
//-1ifallt<0,0otherwise (in which case the line splits the polygon).
positive = 0; negative = 0; zero = 0;
for (i = 0; i < C.N; i++) {
t = Dot(D, S.V(i) - P);
if (t > 0) positive++; else if (t < 0) negative++; else zero++;
if (positive && negative || zero) return 0;
}
return positive?1:-1;
}
An Asymptotically Better Alternative
Although the alternative implementation is roughly twice as fast as the direct imple-
mentation, both are of order O(NM),whereN and M are the number of vertices
for the convex polygons. An asymptotically better alternative uses a form of bisec-
tion to find an extreme point of the projection of the polygon (O’Rourke 1998). The
272 Chapter 7 Intersection in 2D
bisection effectively narrows in on sign changes of the dot product of edges with
the specified direction vector. For a polygon of N vertices, the bisection is of order
O(log N), so the total algorithm is O(max{N log M, M log N }).
Given two vertex indices i
0
and i
1
of a polygon with N vertices, the middle index
of the indices is described by the following pseudocode:
int GetMiddleIndex(int i0, int i1, int N)
{
if (i0 < i1)
return (i0 + i1) / 2;
else
return (i0 + i1 + N)/2%N);
}
The division of two integers returns the largest integer smaller than the real-value
ratio, and the percent sign indicates modulo arithmetic. Observe that if i
0
= i
1
= 0,
the function returns a valid index. The condition when i
0
<i
1
has an obvious result:
the returned index is the average of the input indices, certainly supporting the name
of the function. For example, if the polygon has N = 5 vertices, inputs i
0
= 0 and
i
1
= 2 lead to a returned index of 1. The other condition handles wraparound of
the indices. If i
0
= 2 and i
1
= 0, the implied set of ordered indices is {2, 3, 4, 0}.The
middle index is selected as 3 since 3 = (2 + 0 +5)/2 (mod 5).
The bisection algorithm to find the extreme value of the projection is
int GetExtremeIndex(ConvexPolygon C, Point D)
{
i0=0;i1=0;
while (true) {
mid = GetMiddleIndex(i0,i1);
next = (mid + 1) % C.N;
E = C.V(next) - C.V(mid);
if (Dot(D, E) > 0) {
if (mid != i0) i0 = mid; else return i1;
} else {
prev = (mid + C.N - 1) % C.N;
E = C.V(mid) - C.V(prev);
if (Dot(D, E) < 0) i1 = mid; else return mid;
}
}
}
7.7 The Method of Separating Axes 273
Using the bisection method, the intersection testing pseudocode is
bool TestIntersection(ConvexPolygon C0, ConvexPolygon C1)
{
// Test edges of C0 for separation. Because of the counterclockwise ordering,
// the projection interval for C0 is [m, 0] where m <= 0. Only try to determine
// if C1 is on the ‘positive’ side of the line.
for (i0 = 0, i1 = C0.N - 1; i0 < C0.N; i1 = i0, i0++) {
D = Perp(C0.E(i1)); // C0.E(i1) = C0.V(i0) - C0.V(i1));
min = GetExtremeIndex(C1, -D);
diff = C1.V(min) - C0.V(i0);
if (Dot(D, diff) > 0) {
// C1 is entirely on ‘positive’ side of line C0.V(i0)+t*D
return false;
}
}
// Test edges of C1 for separation. Because of the counterclockwise ordering,
// the projection interval for C1 is [m, 0] where m <= 0. Only try to determine
// if C0 is on the ‘positive’ side of the line.
for (i0 = 0, i1 = C1.N - 1; i0 < C1.N; i1 = i0, i0++) {
D = Perp(C1.E(i1)); // C1.E(i1) = C1.V(i0) - C1.V(i1));
min = GetExtremeIndex(C0, -D);
diff = C0.V(min) - C1.V(i0);
if (Dot(D,diff) > 0) {
// C0 is entirely on ‘positive’ side of line C1.V(i0)+t*D
return false;
}
}
return true;
}
7.7.3 Separation of Moving Convex Polygons
The method of separating axes extends to convex polygons moving with constant
velocity. The algorithm is attributed to Ron Levine in a post to the GD algorithms
mailing list (Levine 2000). If C
0
and C
1
are convex polygons with velocities w
0
and
w
1
, it can be determined via projections if the polygons will intersect for some time
T ≥ 0. If they do intersect, the first time of contact can be computed. It is enough to
work with a stationary polygon C
0
and a moving polygon C
1
with velocity w since we
can always use w =w
1
−w
0
to perform the calculations as if C
0
were not moving.
