Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

284 Chapter 7 Intersection in 2D

// edge-edge intersection

P = C1.V(Cfg1.index[1]) + tfirst * W1;

E = C1.E(Cfg1.index[1]);

U0 = C0.V(Cfg0.index[0]);

U1 = C0.V((Cfg0.index[0] + 1) % C0.N);

s0 = Dot(E, U1 - P) / Dot(E, E);

s1 = Dot(E, U0 - P) / Dot(E, E);

FindIntervalIntersection(0, 1, s0, s1, quantity, interval);

for (i = 0; i < quantity; i++)

I[i]=P+interval[i] * E;

}

} else { // polygons were initially intersecting

ConvexPolygon C0Moved = C0 + tfirst * W0;

ConvexPolygon C1Moved = C1 + tfirst * W1;

FindPolygonIntersection(C0Moved, C1Moved, quantity, I);

}

The ﬁnal case occurs when the two polygons were initially overlapping, so the ﬁrst

time of contact is T = 0.

FindPolygonIntersection is a general routine for computing

the intersection of two polygons.

Chapter

8Miscellaneous 2D

Problems

This chapter includes a variety of problems involving lines, circles, and triangles.

Most of these are commonly (or at least occasionally) encountered problems, while

others, although less commonly encountered, serve to show how various techniques

may be brought to bear on new problems.

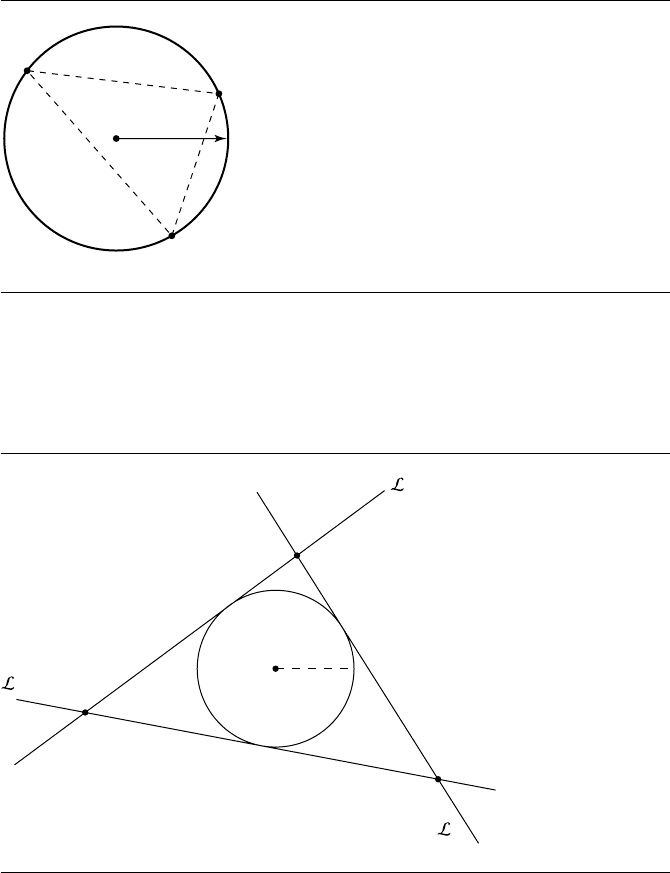
8.1 Circle through Three Points

Suppose we have three points P

, P

, and P

. These three points deﬁne a unique

circle C : {C, r}, as shown in Figure 8.1. This problem is equivalent to ﬁnding the

circumscribed circle of the triangle formed by the three vertices, the solution to which

can be found in Section 13.10.

8.2

Circle Tangent to Three Lines

Suppose we have three lines L

, L

, and L

. If none of these lines are parallel, then

a unique circle C : {C, r} can be found that is tangent to all three lines, as shown in

Figure 8.2.

The intersections of the three lines form a triangle, and so this problem is equiva-

lent to ﬁnding what is known as the inscribed circle or incircle of a triangle. If we ﬁrst

compute these intersections, our problem is then equivalent to ﬁnding the inscribed

circle of the triangle so formed, the solution to which can be found in Section 13.10.

285

286 Chapter 8 Miscellaneous 2D Problems

Figure 8.1 Circle through three points.

Figure 8.2 Circle tangent to three lines.

8.3 Line Tangent to a Circle at a Given Point 287

P – C

Figure 8.3 Line tangent to a circle at a given point.

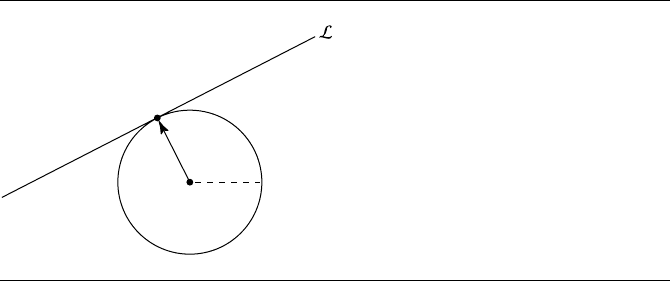
8.3 Line Tangent to a Circle at a Given Point

Figure 8.3 shows the construction of a line through a given point on a circle and

tangent to it. Computation of the line in parametric form is trivial

L : {P , (P − C)

⊥

}

or in coordinate terms

x =P

− t(P

− C

)

y =P

+ t(P

− C

)

The implicit form is equally trivial to compute:

L : {P − C, −((P − C) · P)}

The pseudocode is

void LineTangentToCircleAtGivenPoint(Line2D line, Point2D c, Point2D p)

{

Vector2Dv=p-c;

line.direction.x = -v.y;

line.direction.y = v.x;

line.origin = p;

}

288 Chapter 8 Miscellaneous 2D Problems

Figure 8.4 Line through point, tangent to a circle.

Two solutions One solution No solution

Figure 8.5 In general, there are two tangents, but there may be one or none.

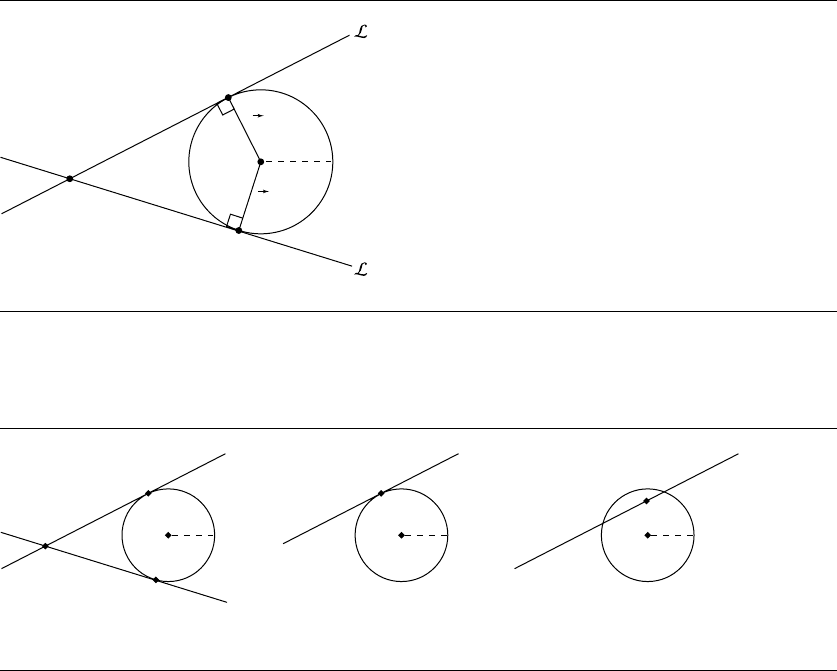
8.4

Line Tangent to a Circle through a Given

Point

Suppose we have a circle C, deﬁned by its center C and radius r, and a point P , and

we wish to compute the lines L

and L

through P and tangent to C, as shown in

Figure 8.4. Note that for an arbitrary point P and circle C, there may be one, two, or

no tangents, as can be seen in Figure 8.5.

The key to the solution here is in noting that the direction vector of L

)is

perpendicular to vectors v

(v

) between the center of C and point(s) Q

)onC.

Consider the angle θ between v (either one) and u = P − C: using the deﬁnition of

the dot product, we know that

8.4 Line Tangent to a Circle through a Given Point 289

cos θ =

u ·v

uv

But we also know by trigonometry that

cos θ =

u

If we equate these, we get

v ·u

uv

u

If we note that v=r, we can simplify this as follows:

u ·v

uv

u

u ·v

ru

u

u ·v = r

We now have two equations

u ·v = r

v=r

where u and r are known and v comprises two unknowns. In component form, we

have

+ u

= r



+ v

= r

which we can solve for the two unknowns v

and v

−

∓



−

(

)



−





+ r

+ u

290 Chapter 8 Miscellaneous 2D Problems

The two vectors v

and v

can be obtained by computing both combinations of the

+/−and −/+appearing in the equation above. The tangent lines are perpendicular

to v

and v

, and so we have the two tangents:

(t) = P +t v

⊥

(t) = P −t v

⊥

The pseudocode is

int TangentLineToCircleThroughPoint(

Point2D p,

float radius,

Point2D center,

Line solution[2])

{

int numSoln;

float distanceCP;

distanceCP = dist2D(center,p);

Vector2D u, v0, v1;

if (distanceCP < radius) {

numSoln = 0;

} else if (distanceCP == radius) {

numSoln = 1;

u=p-center;

solution[0].setDir(-u.y, u.x);

solution[0].setPoint(p.x, p.y);

} else if (distanceCP > radius) {

numSoln = 2;

u=p-center;

float ux2 = u.x * u.x;

float ux4 = ux2 * ux2;

float uy2 = u.y * u.y;

float r2 = radius * radius;

float r4 = r2 * r2;

float num = r2 * uy2;

float denom = ux2 + uy2;

float rad = sqrt(-(r4 * ux2) + r2 * ux4 + r2 * ux2 * uy2);

v0.x = (r2 - (num + u.y * rad)/denom)/u.x

v0.y = (r2 * u.y) + rad)/ denom;

8.5 Lines Tangent to Two Circles 291

v1.x = (r2 - (num - u.y * rad)/denom)/u.x

v1.y = (r2 * u.y) - rad)/ denom;

solution[0].setDir(-v0.y, v.x);

solution[0].setPoint(p.x, p.y);

solution[1].setDir(v1.y, -v1.x)

solution[1].setPoint(p);

// Note: may wish to normalize line directions

// before returning, depending on application

}

return numSoln;

}

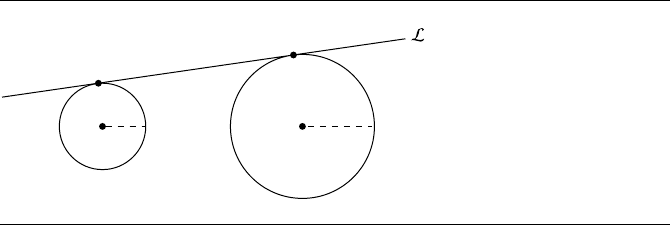
8.5 Lines Tangent to Two Circles

Given two circles, we wish to ﬁnd a line tangent to both circles, as shown in Figure 8.6.

The circles are deﬁned by their respective centers and radii: {C

, r

} and {C

, r

}.As

can be seen in Figure 8.7, in general there can be four, two, one, none, or an inﬁnite

number of tangents. In our solution, we’ll assume that the two circles neither contain

nor intersect one another; this condition is satisﬁed if C

− C

 >r

+ r

We’ll solve for the lines in parametric form, L : X(t) = P + t

d, and assume that

≥ r

. A line intersecting the ﬁrst circle satisﬁes

=X(t) − C



= t

+ 2(

d · (P − C

))t +P − C



(8.1)

Figure 8.6 Line tangent to two circles.

292 Chapter 8 Miscellaneous 2D Problems

Four tangents

One tangent

Zero tangents Infinite tangents

, r

, C

Two tangents

Figure 8.7 Depending on the relative sizes and positions of the circles, the number of tangents between

them will vary.

For the line to be tangent at the point of intersection, the line must also satisfy

0 =

d · (X(t) − C

) = t +

d · (P − C

) (8.2)

If we solve for t in Equation 8.2, and substitute it back into Equation 8.1, we get

=P − C



− (

d · (P − C

))

(8.3)

For the second circle, we can apply the same steps and get

=P − C



− (

d · (P − C

))

(8.4)

8.5 Lines Tangent to Two Circles 293

The point P can be chosen on the line containing C

and C

, the centers of the

circle. Let P = (1 − s)C

+ sC

, for some s, and let w = C

− C

. Then

P − C

= s w

P − C

= (s − 1) w

If we substitute these back into Equations 8.3 and 8.4 we get

= s

(w

− (

d ·w)

)

= (s − 1)

(w

− (

d ·w)

)

So r

= r

/(s −1)

,or

− r

+ 2r

s −r

= 0

If the two circles have the same radius (that is, r

), then s =1/2, and thus P is the

midpoint of the line segment between C

and C

, the centers of the circles. Moreover

(

d ·w)

=w

− 4r

= a

> 0

and so

d ·w = a (of course, we could use −a as the root, but this just leads to a

direction vector with the opposite sign). If we let

d = (d

, d

), then

d ·w =a is the

equation for a line. The constraint 

d

=1 corresponds to a circle. The two together

represent the intersection of a line with a circle. Either solution will do.

Let w =(w

, w

). Then w

+ w

= a and d

+ d

= 1. If |w

|≥|w

|, then

= (a −w

)/w

and

+ w

− 2aw

+ a

− w

= 0

If |w

|≥|w

|, then d

= (a −w

)/w

and

+ w

− 2aw

+ a

− w

= 0

In either case, the two roots lead to two direction vectors for the tangent lines.

If r

, the quadratic in s has two real-valued solutions. From the geometry,

one of the values must satisfy 0 <s<1 and produces the two tangents that intersect

each other between the two circles (L

and L

in the “Four tangents” case in Fig-

ure 8.7). The other root cannot be s = 0 (otherwise P would be at a circle center,

which is not possible).

Foreachroots, the same idea as in the case r

works. The quadratic to solve

(

d ·w)

=w

− r

= a

> 0