Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

294 Chapter 8 Miscellaneous 2D Problems

Also,

(

d ·w)

=w

− r

/(s −1)

= a

> 0

The ﬁrst equation should be used when s

≥(s −1)

; otherwise, use the second one.

The same quadratics may be set up for d

or d

(a has a different value, though) and

solved.

The pseudocode is

void GetDirections(

Vector2D w,

double a,

Vector2D& dir0,

Vector2D& dir1)

{

double aSqr=a*a;

double wxSqr = w.x * w.x;

double wySqr = w.y * w.y;

double c2 = wxSqr + wySqr, invc2 = 1.0 / c2;

double c0, c1, discr, invwx, invwy;

if (fabs(w.x) >= fabs(w.y)) {

c0 = aSqr - wxSqr;

c1=-2.0*a*w.y;

discr = sqrt(fabs(c1 * c1 - 4.0 * c0 * c2));

invwx = 1.0 / w.x;

dir0.y = -0.5 * (c1 + discr) * invc2;

dir0.x = (a - w.y * dir0.y) * invwx;

dir1.y = -0.5 * (c1 - discr) * invc2;

dir1.x = (a - w.y * dir1.y) * invwx;

} else {

c0 = aSqr -w ySqr;

c1=-2.0*a*w.x;

discr = sqrt(fabs(c1 * c1 - 4.0 * c0 * c2));

invwy = 1.0 / w.y;

dir0.x = -0.5 * (c1 + discr) * invc2;

dir0.y = (a - w.x * dir0.x) * invwy;

dir1.x = -0.5 * (c1 - discr) * invc2;

dir1.y = (a - w.x * dir1.x) * invwy;

}

int LinesTangentToTwoCircles(

Circle2D circle0,

8.5 Lines Tangent to Two Circles 295

Circle2D circle1,

Line2D line[4])

{

Vector2Dw={circle1.center.x - circle0.center.x,

circle1.center.y - circle0.center.y };

double wLenSqr = w.x * w.x + w.y * w.y;

double rSum = circle0.radius + circle1.radius;

if (wLenSqr <= rSum * rSum) {

return 0; // circles are either intersecting or nested

}

double epsilon = 1e-06;

double rDiff = circle1.radius - circle0.radius;

if (fabs(rDiff) >= epsilon) {

// solve (R1^2-R0^2)*s^2 + 2*R0^2*s - R0^2 = 0.

double R0sqr = circle0.radius * circle0.radius;

double R1sqr = circle1.radius * circle1.radius;

double c0 = -R0sqr;

double c1 = 2.0 * R0sqr;

double c2 = circle1.radius * circle1.radius - R0sqr, invc2 = 1.0 / c2;

double discr = sqrt(fabs(c1 * c1 - 4.0 * c0 * c2));

double s, oms, a;

// first root

s = -0.5 * (c1 + discr) * invc2;

line[0].p.x = circle0.center.x+s*w.x;

line[0].p.y = circle0.center.y+s*w.y;

line[1].p.x = line[0].p.x;

line[1].p.y = line[0].p.y;

if (s >= 0.5) {

a = sqrt(fabs(wLenSqr - R0sqr / (s * s)));

} else {

oms = 1.0-s;

a = sqrt(fabs(wLenSqr - R1sqr / (oms * oms)));

}

GetDirections(w, a, line[0].direction, line[1].direction);

// second root

s = -0.5 * (c1 - discr) * invc2;

line[2].p.x = circle0.center.x+s*w.x;

line[2].p.y = circle0.center.y+s*w.y;

line[3].p.x = line[2].p.x;

line[3].p.y = line[2].p.y;

if (s >= 0.5) {

296 Chapter 8 Miscellaneous 2D Problems

a = sqrt(fabs(wLenSqr - R0sqr / (s * s)));

} else {

oms=1.0-s;

a = sqrt(fabs(wLenSqr - R1sqr / (oms * oms)));

}

GetDirections(w, a, line[2].direction, line[3].direction);

} else {

// circles effectively have same radius

// midpoint of circle centers

Point2 mid =

{

0.5 * (circle0.center.x + circle1.center.x),

0.5 * (circle0.center.y + circle1.center.y)

};

// tangent lines passing through midpoint

double a = sqrt(fabs(wLenSqr - 4.0 * circle0.radius * circle0.radius));

GetDirections(w, a, line[0].direction, line[1].direction);

line[0].p.x = mid.x;

line[0].p.y = mid.y;

line[1].p.x = mid.x;

line[1].p.y = mid.y;

// unitize w

double invwlen = 1.0 / sqrt(wLenSqr);

w.x *= invwlen;

w.y *= invwlen;

// tangent lines parallel to unitized w

// 1. D = w

// 2. a. P = mid + R0 * perp(w), perp(a, b) = (b, -a)

// b. P = mid - R0 * perp(w)

line[2].p.x = mid.x + circle0.radius * w.y;

line[2].p.y = mid.y - circle0.radius * w.x;

line[2].direction.x = w.x;

line[2].direction.y = w.y;

line[3].p.x = mid.x - circle0.radius * w.y;

line[3].p.y = mid.y + circle0.radius * w.x;

line[3].direction.x = w.x;

line[3].direction.y = w.y;

}

return 1;

}

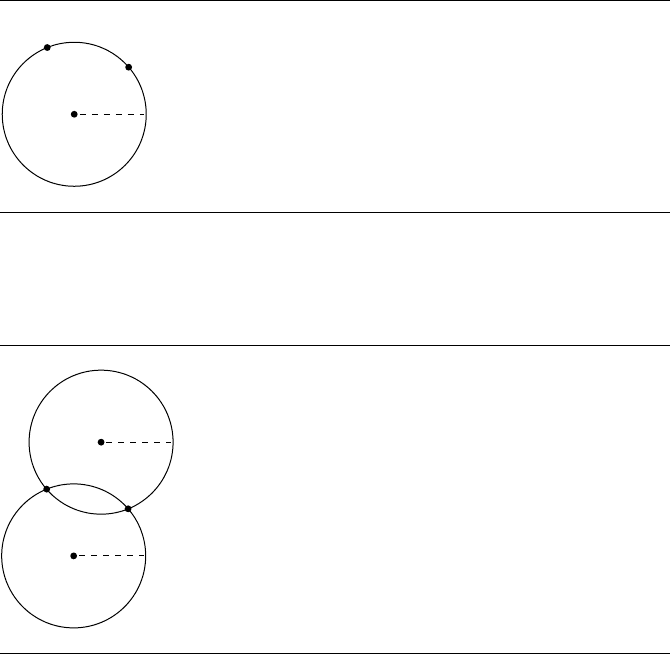
8.6 Circle through Two Points with a Given Radius 297

Figure 8.8 Circle through two points with a given radius.

Figure 8.9

Both possible circles through two points with a given radius.

8.6

Circle through Two Points

with a Given Radius

Given two points P and Q, not coincident, we’d like to ﬁnd a circle passing through

both points. Of course, there are actually an inﬁnite number of such circles, so we

must specify a desired radius r, as shown in Figure 8.8. As usual, there is more

than one solution to this—there are actually two such possible circles, as shown in

Figure 8.9.

The insight for this problem is to note that the desired circle’s center is at the

intersection of two circles of radius r,centeredatP and Q, respectively, as can be

seen in Figure 8.10. That is, we simply create two circles of radius r,centeredatP

and Q, respectively, and compute their intersections—these intersections will be the

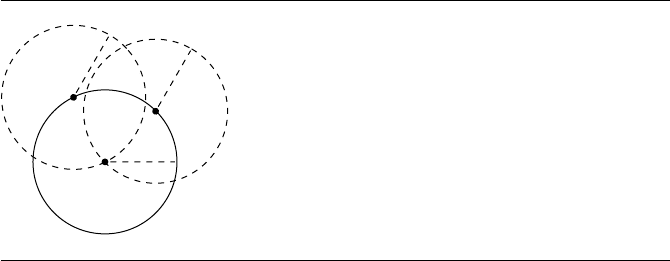
298 Chapter 8 Miscellaneous 2D Problems

Figure 8.10 Insight for computing circle of given radius through two points.

centers of two circles of radius r that pass through P and Q. The solution to the

problem of intersecting two circles can be found in Section 7.5.2.

The pseudocode is

CircleThrough2PointsGivenR(Point2D p1, Point2D p2, float radius,

Point2D centers[2])

{

// See Section 7.5.2

FindIntersectionOf2DCircles(p1, p2, radius, radius, centers);

}

8.7 Circle through a Point and Tangent

to a Line with a Given Radius

Suppose we have a line L and a point P . The problem is to ﬁnd a circle C with a

given radius r that is tangent to the line and passes through the point, as shown in

Figure 8.11. Of course, there are actually two (potential) such circles, as we can see in

Figure 8.12.

Other possible conﬁgurations are to have the point P lying on the line, or to have

P lying at a distance from L greater than 2r. In the ﬁrst case, there are two solutions,

but they lie on either side of the line; in the second case, there are no solutions, as

seen in Figure 8.13.

The insight for this problem comes from the observation that the center C of C

must be at a distance r from L. Furthermore, aside from the case where P lies on L,

C must be on the same side of the line as P .

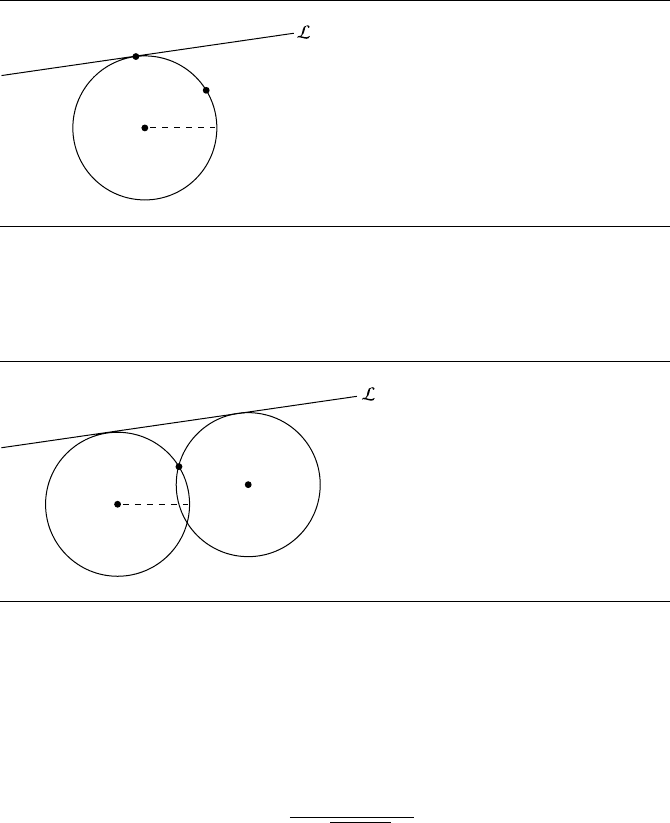
8.7 Circle through a Point and Tangent to a Line with a Given Radius 299

Figure 8.11 Circle through a point and tangent to a line with a given radius.

Figure 8.12 In general, there are two distinct circles through the given point.

If the line is given in implicit form L : ax +by +c =0, then the (signed) distance

from P to L is

r =

+ bC

+ c

√

+ b

We also know that the circle must pass through P , and so that point must satisfy the

circle’s equation:

− P

)

+ (C

− P

)

= r

This gives us, generally speaking, two equations in two unknowns. It is certainly

possible to simply solve these two equations for {C

, C

}, but this yields

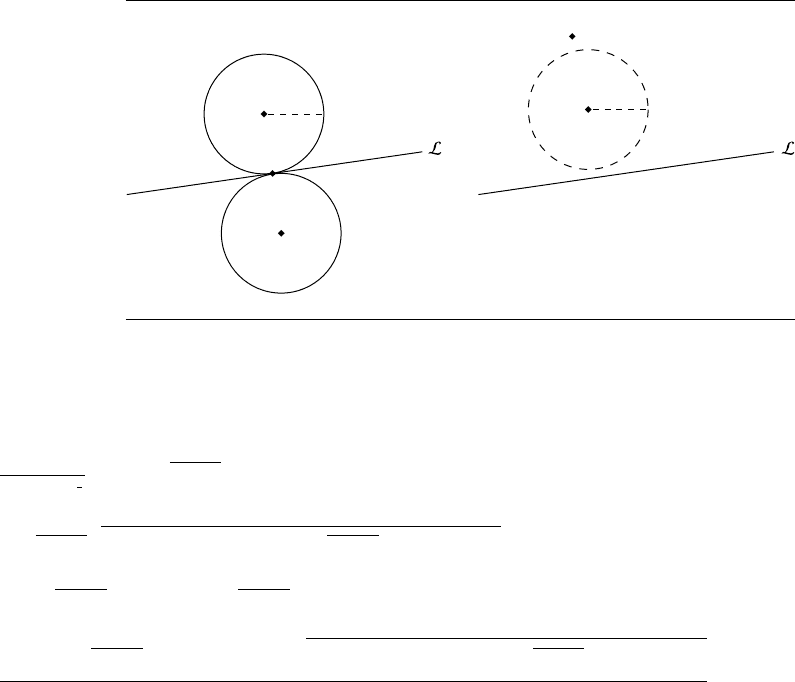
300 Chapter 8 Miscellaneous 2D Problems

Figure 8.13 If P lies on the line, the circles are mirrored across the line; if P is further from the

line than the diameter of the circle, there are no solutions.



+ b



r + ab



+ b

− b



+ b



−





c + aP

+ bP





c − 2



+ b

r + aP

+ bP



− a





+ b

c + b



−

(

)



+ b



(8.5)

−



c −

√

+ b

r + aP



+ a



−





c + aP

+ bP





c − 2

√

+ b

r + aP

+ bP



+ b

(8.6)

There are several ways to approach solving this (see Chasen 1978 and Bowyer and

Woodwark 1983). Following Bowyer and Woodwark (1983), we translate the entire

system so that P is at the origin; this of course doesn’t change the a and b coefﬁcients

of L, but only the constant c:



= c + aP

+ bP

Then, we check the sign of c



. If it is negative, we multiply the equation through

(entirely) by −1 (we could have arbitrarily preferred a negative value for c and com-

pensated in the subsequent equations). If L is normalized, Equations 8.5 and 8.6

simplify to

8.7 Circle through a Point and Tangent to a Line with a Given Radius 301

=−a(c



− r) ± b



−c



+ 2c



=−b(c



− r) ∓ a



−c



+ 2c



The pseudocode is

int CircleThroughPointTangentToLineGivenRadius(

Point2D point,

Line2D line,

float radius,

Point2D center[2])

{

// Returns number of solutions

// Translate line so point is at origin

float cPrime = line.c + line.a * point.x + line.b * point.y;

// Check if point lies on, or nearly on, the line

if (Abs(cPrime) < epsilon) {

Vector2D tmp = { line.a, line.b };

center[0] = point + tmp * r;

center[1] = point - tmp * r;

return 2;

}

float a;

float b;

float c;

if (cPrime < 0) {

// Reverse line

a = -line.a;

b = -line.b;

c = -line.c;

} else {

a = line.a;

b = line.b;

c = line.c;

}

float tmp1 = cPrime - radius;

float tmp2=r*r+tmp1 * tmp1;

if (tmp2 < -epsilon) {

// No solutions - point further away from

302 Chapter 8 Miscellaneous 2D Problems

// line than radius.

return 0;

}

if (tmp2 < epsilon) {

// One solution only

center[0].x = point.x-a*tmp1;

center[0].y = point.y-b*tmp1;

return 1;

}

// Otherwise, two solutions

tmp2 = Sqrt(tmp2);

Point2D tmpPt = { point.x-a*tmp1, point.y-b*tmp1 };

center[0] = { tmpPt+b*tmp2, tmpPt-a*tmp2 };

center[1] = { tmpPt-b*tmp2, tmpPt+a*tmp2 };

return 2;

}

8.8 Circles Tangent to Two Lines

with a Given Radius

Suppose we have two nonparallel lines L

and L

. A circle C with a given radius r can

be constructed so that it is tangent to both lines, as shown in Figure 8.14. Of course,

there are actually four such circles, as shown in Figure 8.15.

Given the two lines L

and L

, and the radius r, our problem is to ﬁnd the circles’

centers C

, C

, and C

. The insight here begins with the observation that each of

is at a distance r from both L

and L

.IfC

is to be at a distance r from L

, then

it must be somewhere on a line that is parallel to L

and is separated by a distance

r;ifC

is to be at a distance r from L

, then it must be somewhere on a line that is

parallel to L

and is separated by a distance r as well.

Thus, the circle center C

must be at the intersection of these two lines that are

parallel to, and at a distance r from, L

and L

, respectively, as shown in Figure 8.16

for one of the four circles. All four possible tangential circles are constructed by

considering all pairs of intersections between the two lines parallel to L

and the two

lines parallel to L

If the two lines are deﬁned implicitly

: a

x +b

y +c

= 0

: a

x +b

y +c

= 0

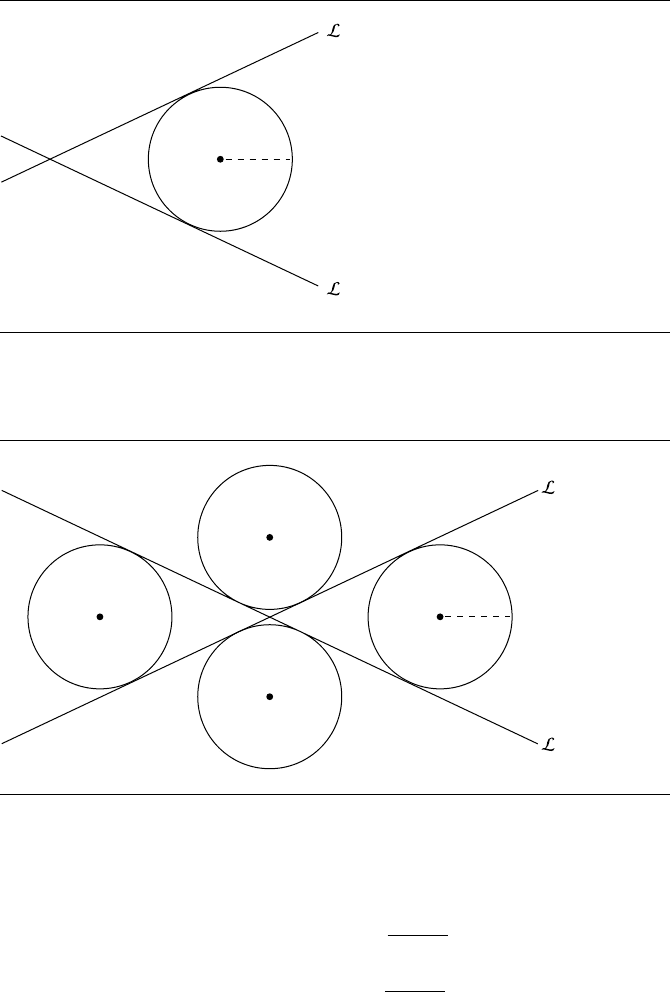
8.8 Circles Tangent to Two Lines with a Given Radius 303

Figure 8.14 Circles tangent to two lines with a given radius.

Figure 8.15 In general, there are four circles of a given radius tangent to two lines.

then the two lines parallel to these, at a distance r from each, are

: a

x +b

y +c



+ b

= 0

: a

x +b

y +c



+ b

= 0