Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

304 Chapter 8 Miscellaneous 2D Problems

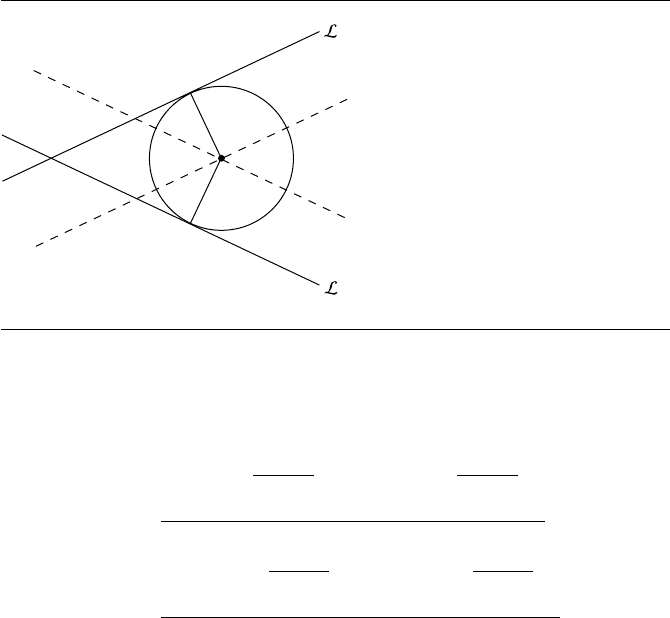
Figure 8.16 Constructive approach for circle tangent to two lines.

If we solve for x and y, we’ll have the circles’ centers:

x =−





+ b



− b





+ b



−a

+ a

y =−

−a





+ b



+ a





+ b



−a

+ a

The pseudocode is

void CircleTangentToLinesGivenR(Line2D l0, Line2D l1, float radius, Point2D center[4])

{

float discrm0 = sqrt(l0.a * l0.a + l0.b * l0.b) * r;

float discrm1 = sqrt(l1.a * l1.a + l1.b * l1.b) * r;

float invDenom = 1.0 / (-l1.a * l0.b + l0.a * l1.b);

center[0].x = -(l1.b * (l0.c + discrm0) - l0.b * (l1.c + discrm1)) * invDenom;

center[0].y = -(l1.a * (l0.c + discrm0) - l0.a * (l1.c + discrm1)) * invDenom;

center[1].x = -(l1.b * (l0.c + discrm0) - l0.b * (l1.c + discrm1)) * invDenom;

center[1].y = -(l1.a * (l0.c - discrm0) - l0.a * (l1.c - discrm1)) * invDenom;

center[2].x = -(l1.b * (l0.c - discrm0) - l0.b * (l1.c - discrm1)) * invDenom;

center[2].y = -(l1.a * (l0.c - discrm0) - l0.a * (l1.c - discrm1)) * invDenom;

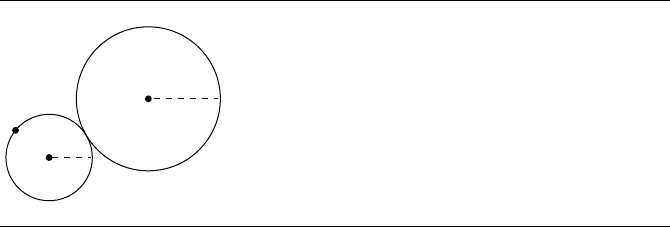
8.9 Circles through a Point and Tangent to a Circle with a Given Radius 305

center[3].x = -(l1.b * (l0.c - discrm0) - l0.b * (l1.c - discrm1)) * invDenom;

center[3].y = -(l1.a * (l0.c + discrm0) - l0.a * (l1.c + discrm1)) * invDenom;

}

8.9 Circles through a Point and Tangent

to a Circle with a Given Radius

Given a circle C

: {C

, r

} and a point P , the problem is to ﬁnd a circle C

: {C

, r

with a given radius, that passes through the point and is tangent to the given circle

(see Figure 8.17). As is typical with problems involving tangents, there are, in general,

two solutions. If P is further from C

than r

+ 2r, or closer than r

− 2r, then no

solution is possible. Depending on the relative sizes of the circles, and the placement

of P , one of the circles may be contained within the other—and of course, there may

be four solutions, two solutions, or no solutions (see Figure 8.18). This particular

problem is interesting because it can be solved in (at least) two entirely different

ways—one more analytical and one more constructive.

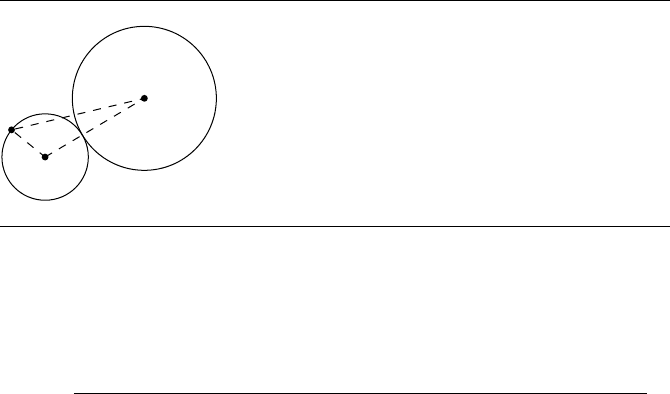
The more analytical approach is based on the fact that we know the lengths of the

sides of the triangle (P , C

, C

) (see Figure 8.19). Clearly, if circle C

is tangent to C

then C

− C

=r

+ r

. The given point P is on the circle, and so P −C

=r

Finally, both P and C

are given. Note that this approach works even when P is

actually on circle C

, in which case the triangle degenerates to a line.

To reduce calls to the square root function, we can instead consider the squared

distances. To further simplify the equations, we can translate the system so that one of

the points is at the origin, then solve it, and translate the solution back; we arbitrarily

choose to translate P to the origin. This yields a system of two equations in two

unknowns {C

1,x

, C

1,y

}

Figure 8.17

Circles through a point and tangent to a circle with a given radius.

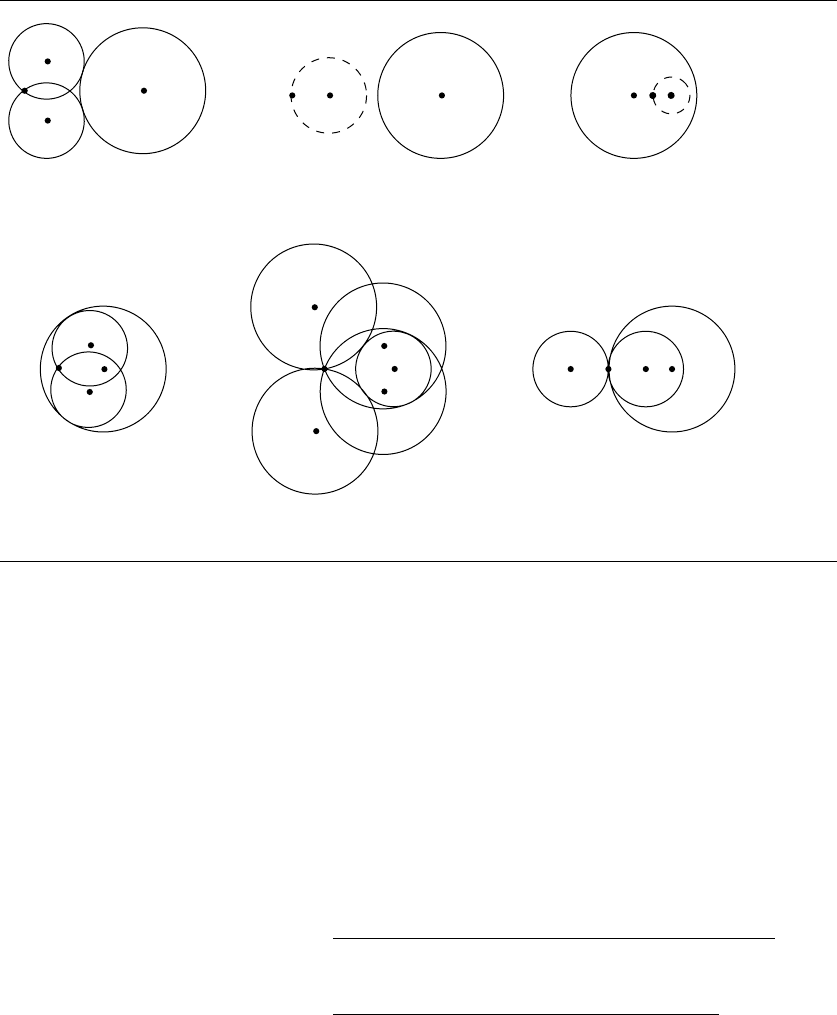
306 Chapter 8 Miscellaneous 2D Problems

No external

No internalTwo external

Two internal

Two external, two internal

One external, one internal

Figure 8.18 Depending on the relative positions and radii of the circle, there may be four, two, or no

solutions.



−C

0,x

+ C

1,x





−C

0,y

+ C

1,y





+ r



1,x

+ C

1,y

= r

(8.7)

whose solution (with the translation put back in) is

1,x

= P

−



0,x



− 2r

0,x

+ C

0,x

+ C

0,x

0,y

∓ C

0,y

0,x



0,x

+ C

0,y



1,y

= P

−



0,y



− 2r

0,y

+ C

0,x

0,y

+ C

0,y

± k



0,x

+ C

0,y



(8.8)

8.9 Circles through a Point and Tangent to a Circle with a Given Radius 307

Figure 8.19 Insight for solving problem.

where

k =



−



0,x



−r

+ C

0,x

+ C

0,y



−r

− 4r

+ C

0,x

+ C

0,y



The pseudocode is

int CircleThroughPTangentToC(Point2D p, Circle2D cIn, float r1, Circle2D cOut[4]

{

float distanceCPS = Distance2D(p, cIn.center);

int numSoln;

if (distanceCP > cIn.radius+2*r1){

numSoln = 0;

} else if (distanceCP < cIn.radius-2*r1){

numSoln = 0;

} else {

numSoln = 4;

float k = sqrt(-(cIn.x^2 * (-cIn.radius^2 + cIn.x^2 + cIn.y^2)) *

(-cIn.radius^2-4*cIn.radius * r1-4*r1^2 + cIn.x^2 + cIn.y^2));

float invDenom = 1.0 / (2 * (cIn.x * cIn.x + cIn.y * cIn.y));

float temp1 = -(cIn.radius^2 * cIn.x^2 ) -2 * cIn.radius * r1 * cIn.x ^2

+ cIn.x^4 + cIn.x^2 * cIn.y^2;

float temp2 = -(cIn.radius^2 * cIn.y) -2 * cIn.radius * r1 * cIn.y

+ cIn.x^2 cIn.y + cIn.y^3;

cOut[0].x = (p.x + (temp1 - cIn.y * k) * invDenom) / cIn.x;

cOut[0].y = (p.y + (temp2 + k) * invDenom);

308 Chapter 8 Miscellaneous 2D Problems

cOut[1].x = (p.x + (temp1 + cIn.y * k) * invDenom) / cIn.x;

cOut[1].y = (p.y + (temp2 - k) * invDenom);

k = -k;

cOut[2].x = (p.x + (temp1 - cIn.y * k) * invDenom) / cIn.x;

cOut[2].y = (p.y + (temp2 + k) * invDenom);

cOut[3].x = (p.x + (temp1 + cIn.y * k) * invDenom) / cIn.x;

cOut[3].y = (p.y + (temp2 - k) * invDenom);

}

// Note: all solutions not necessarily unique - calling routine

// should check...

return numSoln;

}

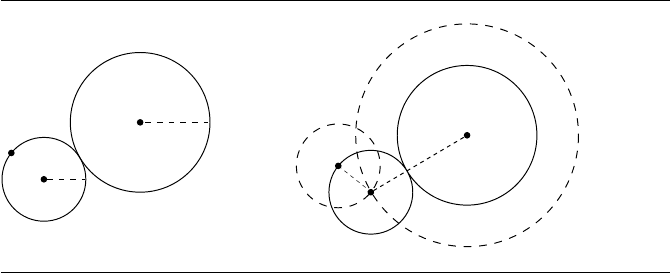
The more “constructive” approach is based on the same observation as the more

“analytic” approach—C

−C

=r

and P −C

=r

. Consider Figure 8.20.

Ifwedrawacircleofradiusr

,centeredatP , it will clearly include C

. If we also

drawacirclecenteredatC

,ofradiusr

+ r

, it will also clearly include C

.So,C

located at the intersection of the two circles so constructed (and the second solution

is centered at the other intersection).

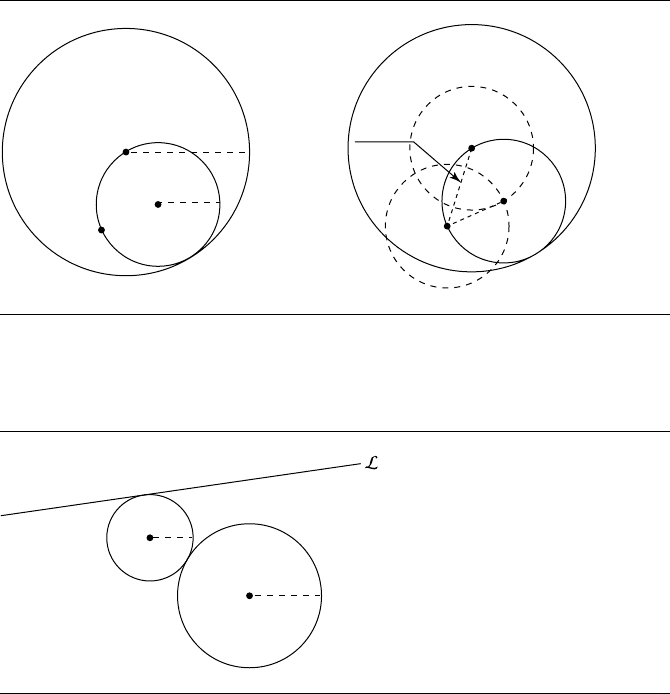
This is very nearly as simple as it appears. The problem is recast as simply ﬁnding

the intersections of the two “auxiliary” circles. The only complication is that you must

consider if P is actually inside C

; in this case, the “auxiliary” circle we draw centered

at C

must have the radius r

− r

(see Figure 8.21). The two cases—P being inside

or outside of C

—can be relatively inexpensively distinguished: if we compare the

squared distance from P and C

to r

, we can avoid an unnecessary square root.

Figure 8.20

Constructive approach to solving problem.

8.10 Circles Tangent to a Line and a Circle with a Given Radius 309

– r

Figure 8.21 Special case for constructive approach.

Figure 8.22 Circles tangent to a line and a circle with a given radius.

8.10

Circles Tangent to a Line and a Circle

with a Given Radius

Suppose we have a circle C

: {C

, r

} and a line L : ax + by + c =0, and we wish to

ﬁnd the circle(s) tangent to both the line and the circle with a given radius, as shown

in Figure 8.22. Of course, there is more than one possible solution; in fact, there are

as many as eight distinct circles, as can be seen in Figure 8.23, or there may be no

solutions, in the case when the distance between C

and L is greater than 2r

,as

in Figure 8.24.

The insight here is to note that C

is at a distance r

from L if it is tangent to it,

and thus is located somewhere along a line L



that is parallel to L and at a distance r

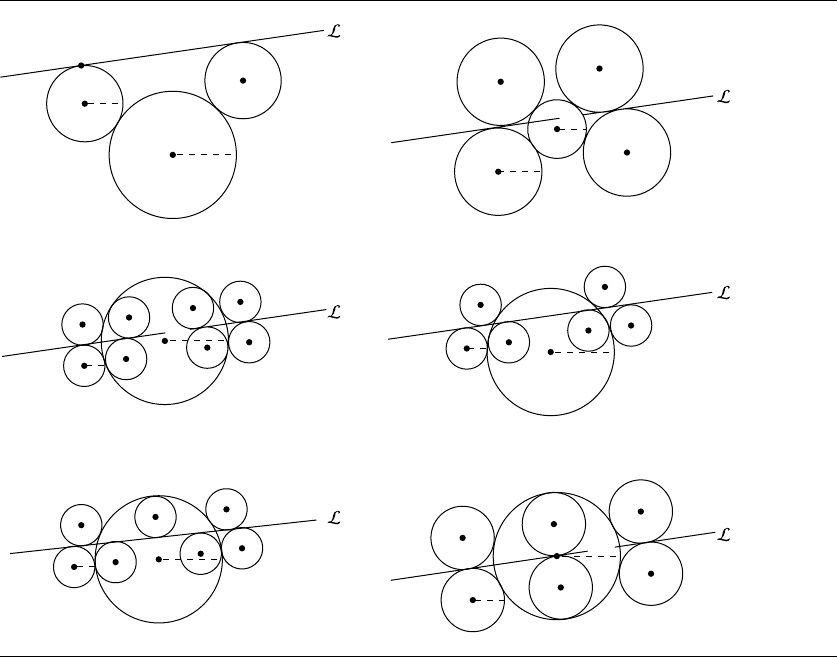
310 Chapter 8 Miscellaneous 2D Problems

Figure 8.23 The number of distinct solutions varies depending on the relative positions of the line and

circle, and the circle’s radius.

from it, as can be seen in Figure 8.25. Further, C

must be at a distance r

+ r

from

if it is tangent to C. Put another way, C

must be on a circle C



: {C

, r

+ r

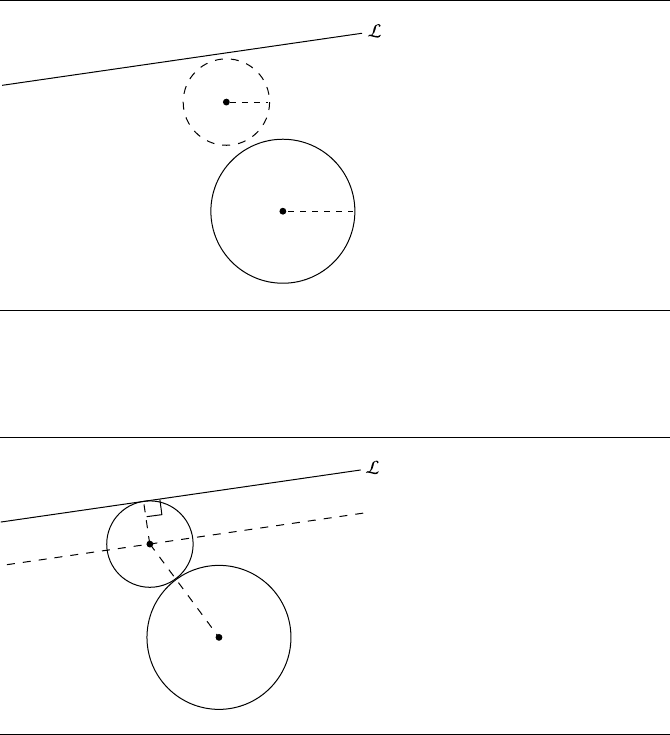
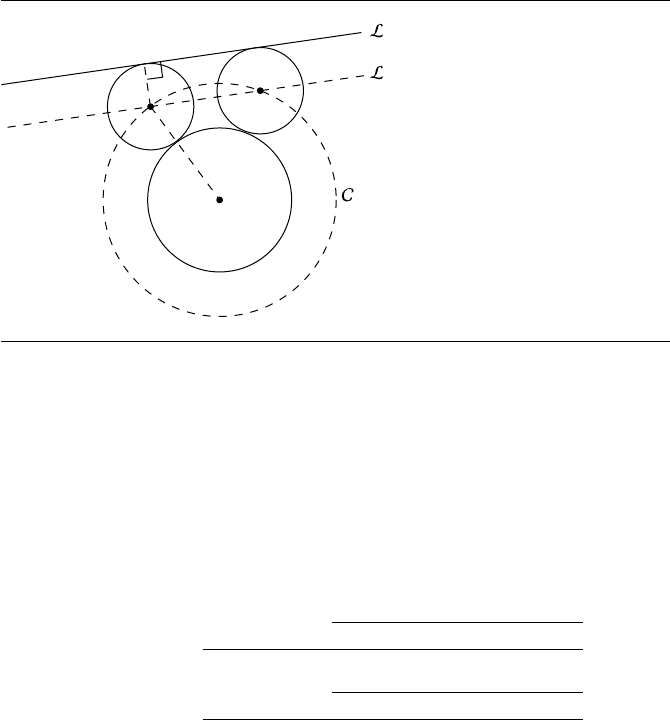
Circles simultaneously tangent to L and C must then be centered at the intersection

of L



and C



(see Figure 8.26).

In order to account for all eight possible tangent circles seen in Figure 8.23, we

need to be able to generate the circles that are “externally” tangent to C

as well as

“internally” tangent. The internally tangent circles are those whose centers are at the

intersection of L



and the circle centered at C

and have the radius r

− r

All of this might seem like it would yield some very complex calculations. How-

ever, if we employ the “trick” described by Bowyer and Woodwark (1983) consisting

of translating the entire thing so that P

is at the origin, it can be much simpliﬁed.

8.10 Circles Tangent to a Line and a Circle with a Given Radius 311

Figure 8.24 No solutions if given radius is too small.

Figure 8.25 Insight for ﬁnding circle of given radius.

We then solve for the center of the desired circles and translate their centers back.

Translating C is trivial—we add its center back into the equation

(x −C

0,x

+ C

0,x

)

+ (y − C

0,y

+ C

0,y

)

+ c = r

which is simply

+ y

= r

312 Chapter 8 Miscellaneous 2D Problems

Figure 8.26 Schematic for the solution.

If our line is in implicit form ax + by + c = 0, the translated line of course has the

same a and b coefﬁcients, and the new c coefﬁcient is simply



= c + aC

0,x

+ bC

0,y

If c



< 0, then we multiply the entire equation through by −1.

The resulting equations for the center of C

are

1,x

= C

0,x

a(c



− r

) ± b



+ b

)(r

± r

)

− (c



− r

)

+ b

1,y

= C

0,y

b(c



− r

) ∓ a



+ b

)(r

± r

)

− (c



− r

)

+ b

The pseudocode is

int CirclesTangentToLineAndCircleGivenRadius(

Line2D l,

Circle2D c,

float radius,

Circle2D soln[8])

{

if (l.distanceToPoint(c.center)>2*radius + c.radius){

return 0;

8.10 Circles Tangent to a Line and a Circle with a Given Radius 313

} else {

// Some of these solutions may be duplicates.

// It is up to the application to deal with this.

float a, b, c;

l.getImplicitCoeffs(a,b,c);

for(i=0;i<8;i++){

soln.radius = radius;

}

float apbSqr = a^2 + b^2;

float cp=c+a*c.center.x+b*c.center.y;

float discrm1 = sqrt(apbSqr * (radius + c.radius)^2 - (cp - radius)^2);

float discrm2 = sqrt(apbSqr * (radius - c.radius)^2 - (cp - radius)^2);

float cpminusr = cp - radius;

soln[0].center.x = c.center.x + (b * cpminusr+b*discrm1) / apbSqr;

soln[0].center.y = c.center.y + (a * cpminusr-a*discrm1) / apbSqr;

soln[1].center.x = c.center.x + (b * cpminusr-b*discrm2) / apbSqr;

soln[1].center.y = c.center.y + (a * cpminusr+a*discrm2) / apbSqr;

soln[2].center.x = c.center.x + (b * cpminusr+b*discrm2) / apbSqr;

soln[2].center.y = c.center.y + (a * cpminusr+a*discrm2) / apbSqr;

soln[3].center.x = c.center.x + (b * cpminusr-b*discrm2) / apbSqr;

soln[3].center.y = c.center.y + (a * cpminusr-a*discrm2) / apbSqr;

soln[4].center.x = c.center.x + (b * cpminusr+b*discrm1) / apbSqr;

soln[4].center.y = c.center.y + (a * cpminusr+a*discrm1) / apbSqr;

soln[5].center.x = c.center.x + (b * cpminusr-b*discrm1) / apbSqr;

soln[5].center.y = c.center.y + (a * cpminusr-a*discrm1) / apbSqr;

soln[6].center.x = c.center.x + (b * cpminusr+b*discrm2) / apbSqr;

soln[6].center.y = c.center.y + (a * cpminusr-a*discrm2) / apbSqr;

soln[7].center.x = c.center.x + (b * cpminusr-b*discrm1) / apbSqr;

soln[7].center.y = c.center.y + (a * cpminusr+a*discrm1) / apbSqr;

return 8;

}