Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

314 Chapter 8 Miscellaneous 2D Problems
C
2
r
2
C
0
r
0
r
1
C
1
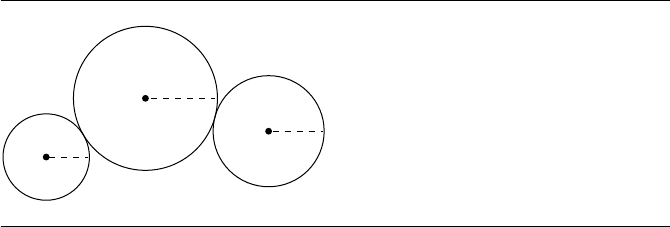
Figure 8.27 Circles tangent to two circles with a given radius.
8.11 Circles Tangent to Two Circles
with a Given Radius
Suppose we have two circles, C
0
: {C
0
, r
0
}and C
1
: {C
1
, r
1
}, and we wish to find a circle
tangent to these two circles and having a given radius, as shown in Figure 8.27. There
are, of course, a variety of possible solutions, depending on the relative positions
of the circles, their radii, and the radius specified for the other circle, as shown in
Figure 8.28.
Our third circle C
2
: {C
2
, r
2
}has a known radius; it is our problem to compute its
center. This circle must be tangent to C
0
and C
1
, which means that its center must be
r
0
+ r
2
from C
0
and r
1
+ r
2
from C
1
. The insight here leading to a solution is to note
that this is equivalent to finding the intersection of two circles centered at C
0
and C
1
,
having radii r
0
+ r
2
and r
1
+ r
2
, respectively, as shown in Figure 8.29. If our original
circles are
C
0
: (x − C
0,x
)
2
+ (y − C
0,y
)
2
= r
2
0
C
1
: (x − C
1,x
)
2
+ (y − C
1,y
)
2
= r
2
1
then they have the equations
C
0
: (x − C
0,x
)
2
+ (y − C
0,y
)
2
= (r
0
+ r
2
)
2
C
1
: (x − C
1,x
)
2
+ (y − C
1,y
)
2
= (r
1
+ r
2
)
2
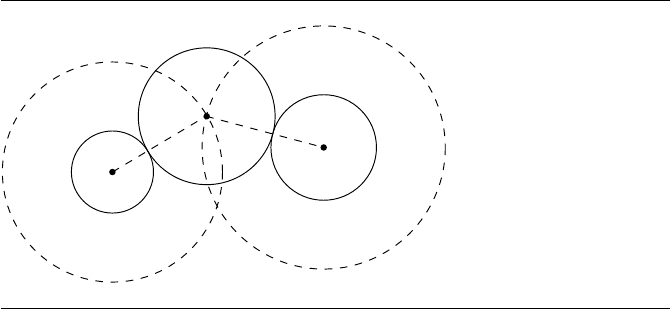
If we compute the intersection of C
0
and C
1
, we’ll have the origins of the circles
tangent to them. The intersection of two circles is covered in Section 7.5.2.
8.11 Circles Tangent to Two Circles with a Given Radius 315
C
2
r
2
C
0
r
0
r
1
C
1
C
3
r
3
= r
2
C
2
C
0
C
1
r
2
r
0
r
1
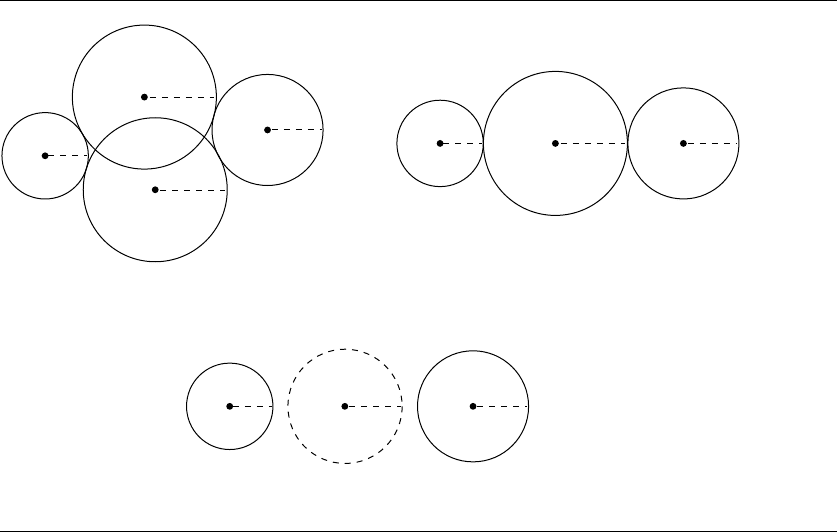
Two solutions
No solutions
One solution
C
2
C
0
C
1
r
2
r
0
r
1
Figure 8.28 In general there are two solutions, but the number of distinct solutions varies with the
relative sizes and positions of the given circles.
The pseudocode is
int CircleTangentToCirclesGivenRadius(
Circle2D c1,
Circle2D c2,
float radius,
Circle2D c[2])
{
Vector2D v = c2.center - c1.center;
float dprod = Dot(v, v);
float dSqr = dprod - (c1.radius + c2.radius)^2;
if (dSqr > radius^2) {
// No solution
return 0;
} else if (dSqr == radius^2) {
float distance = sqrt(dprod);
c.center.x = c1.center.x + (c1.radius + radius) * v.x / distance;
c.center.y = c1.center.y + (c1.radius + radius) * v.y / distance;
316 Chapter 8 Miscellaneous 2D Problems
C
0
C
2
r
2
r
0
r
1
C
1
r
2
Figure 8.29 Construction for a circle tangent to two circles.
c.radius = radius;
return 1;
} else {
Circle2D cp1;
Circle2D cp2;
cp1.center.x = c1.center.x;
cp1.center.y = c1.center.y;
cp1.center.radius = c1.radius + radius;
cp2.center.x = c2.center.x;
cp2.center.y = c2.center.y;
cp2.center.radius = c2.radius + radius;
// Section 7.5.2
findIntersectionOf2DCircles(c1, c2, c);
c[0].radius = radius;
c[1].radius = radius;
return 2;
}
}
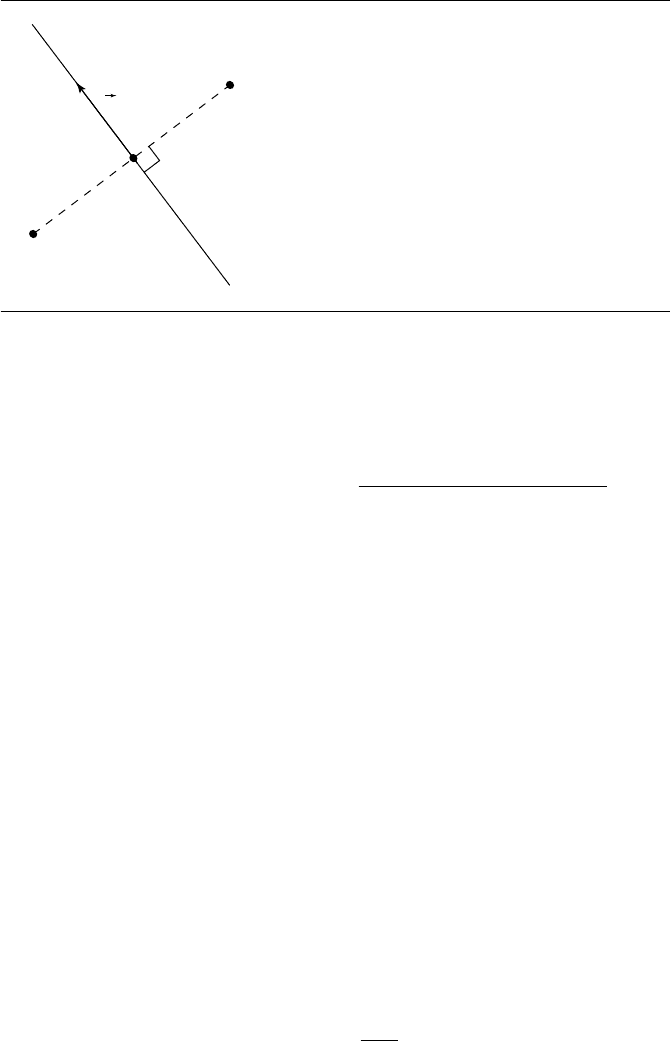
8.12 Line Perpendicular to a Given Line
through a Given Point
Suppose we have a line L
0
and a point Q. Our problem is to find a line L
1
that
is perpendicular to L
0
and passes through Q, as shown in Figure 8.30. If L
0
is in
implicit form, a
0
x +b
0
y +c
0
= 0, then the equation for L
1
is
b
0
x −a
0
y +(a
0
Q
y
− b
0
Q
x
) = 0 (8.9)

8.13 Line between and Equidistant to Two Points 317
Q
1
0
Figure 8.30 Line normal to a given line and through a given point.
If the line is in parametric form, L
0
(t) = P
0
+ t
d, then the equation for L
1
is
L
1
(t) = Q + t
d
⊥
The pseudocode is
LineNormaltoLineThroughPoint(Line2D l0, Point2D q, Line2D& lOut)
{
lOut.origin = q;
Vector2D dPerp;
dPerp.x = -l0.y;
dPerp.y = l0.x;
lOut.direction = dPerp;
}
8.13 Line between and Equidistant to Two Points
Suppose we have two points Q
0
and Q
1
, not coincident, and we wish to find the line
that runs between them and is at an equal distance from them (see Figure 8.31). Of
course, any line passing through a point midway between Q
0
and Q
1
satisfies the
criterion of being an equal distance from them, but by “between” here we mean that
the line should be perpendicular to the vector Q
1
− Q
0
; thus, this problem can be
thought of as finding the perpendicular bisector of the line segment defined by the
two points.
The parametric representation requires a point and a direction; clearly, the point
P = Q
0
+
(Q
1
−Q
0
)
2
is on the line. As
d is simply (Q
1
− Q
0
)
⊥
,wehave
L(t) = Q
0
+
(Q
1
− Q
0
)
2
+ t(Q
1
− Q
0
)
⊥
(8.10)
318 Chapter 8 Miscellaneous 2D Problems
Q
1
Q
0
P
d
Figure 8.31 Line between and equidistant to two points.
The implicit form can be computed just as easily:
(Q
1,x
− Q
0,x
)x +(Q
1,y
− Q
0,y
)y −
(Q
2
1,x
+ Q
2
1,y
) − (Q
2
0,x
+ Q
2
0,y
)
2
The pseudocode is
LineBetweenAndEquidistantTo2Points(Point2D q0, Point2D q1, Line2D& line)
{
line.origin.x = q0.x + (q1.x - q0.x) / 2;
line.origin.y = q0.y + (q1.y - q0.y) / 2;
line.direction.x = (q0.y - q1.y);
line.direction.y = (q1.x - q0.x);
}
8.14 Line Parallel to a Given Line
at a Given Distance
Suppose we have a line L
0
and wish to construct another line L
1
parallel to it
at a given distance d, as shown in Figure 8.32. If the line is in parametric form
L
0
(t) = P
0
+ t
d
0
, then a line parallel to it clearly has the same direction vector. By
noting that the origin of L
1
must be on a line perpendicular to
d
0
, it’s easy to see that
P
1
= P
0
+
d
d
⊥
0
d
0

8.14 Line Parallel to a Given Line at a Given Distance 319
P
0
P
1
d
0
d
1
d
Figure 8.32 Line parallel to a given line at a distance d.
This gives us
L
1
(t) = P
0
+
d
d
⊥
0
d
0
+ t
d
0
or
L
1
(t) = P
0
+
d
d
⊥
0
d
0
+ t
d
0
or simply
L
1
(t) = P
0
+ d
ˆ
d
⊥
0
if L
0
is normalized.
If the line is in implicit form ax + by + c = 0,thenwehave
d =
±(ax+by+c)
−
√
a
2
+b
2
b ≥ 0
±(ax+by+c)
√
a
2
+b
2
b<0
The plus sign in the numerator is used if we want the line above the given line, and the
negative sign is used if we want the line below the given line. If we plug in the desired
distance and simplify, we get the equation for the desired line.
For example, if we have a line L :5x −
√
11y − 7 = 0 and want the line 8 units
above it, we’d have
8 =
5x −
√
11y − 7
−
5
2
+ (−
√
11)
2

320 Chapter 8 Miscellaneous 2D Problems
which simplifies to
5x −
√
11y + 39 = 0
The pseudocode is
LineParallelToGivenLineAtGivenDistance(Line2D l1, Line2D& lOut, float distance)
{
// Assumes l1 is not normalized
lOut.direction = l1.direction;
Vector2D dPerp;
// Chose the perpendicular vector direction
// Two answers are possible though.
dPerp.x = -l1.direction.y;
dPerp.y = l1.direction.x;
float length = dPerp.length();
lOut.origin = l1.origin + distance * dPerp / length;
}
8.15 Line Parallel to a Given Line at a Given
Vertical (Horizontal) Distance
Suppose we have a given line L(t) = P + t
d and wish to find the line at a given
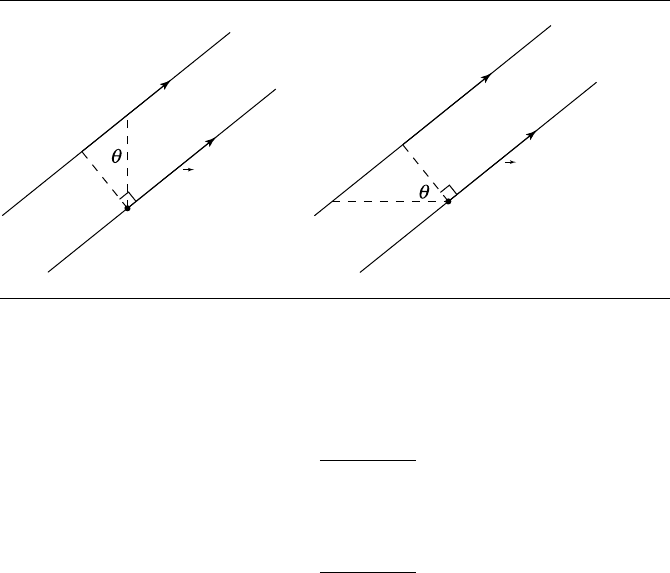
vertical distance v or given horizontal distance h from L, as shown in Figure 8.33.
If we can compute the perpendicular distance d from h (or v), then this reduces to
the previous problem. Using simple trigonometry, we have
cos θ =
d
v
or
cos θ =
d
h
for the vertical and horizontal cases, respectively. We can solve these for d
v cos θ = d
or
h cos θ = d
8.15 Line Parallel to a Given Line at a Given Vertical (Horizontal) Distance 321
P
d
P
d
h
d
d
v
Figure 8.33 Line parallel to a given line at a vertical or horizontal distance d.
respectively. The cosine of the angle θ is easy to compute:
cos θ =
d
⊥
·
[
01
]
d
or
cos θ =
d
⊥
·
[
10
]
d
The pseudocode is
LineParallelToGivenLineAtVorHDistance(Line2D l1, Line2D lOut, float distance,
int vOrH)
{
float cosTheta;
float scalar, length;
Vector2D dPerp;
// Again there is another possible
// perpendicular vector to the one chosen
dPerp.x = -l1.y;
dPerp.y = l1.x;
length = l1.d.length();
if (vOrH) {
// vertical case
322 Chapter 8 Miscellaneous 2D Problems
cosTheta = dPerp.y / length;
} else {
// horizontal case
cosTheta = dPerp.x / length;
}
scalar = distance * cosTheta;
lOut.origin = l1.p + scalar * dPerp / length;
lOut.direction = l1.direction;
}
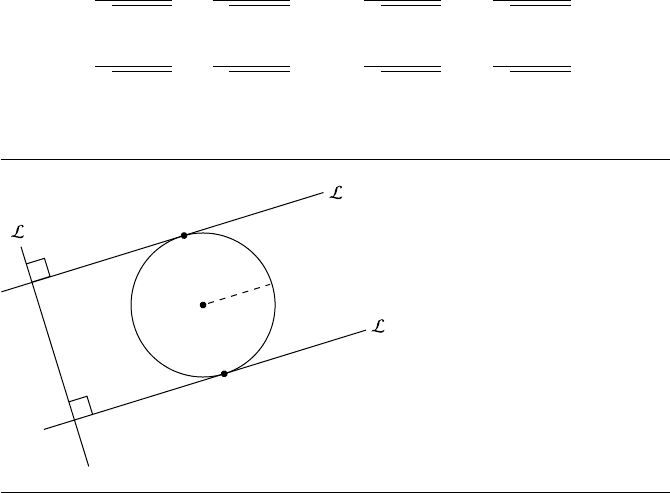
8.16 Lines Tangent to a Given Circle and Normal
to a Given Line
Suppose we have a circle C and line L
0
and we wish to find the lines L
1
and L
2
,
tangent to C and normal (perpendicular) to L
0
, as shown in Figure 8.34.
If the equation of the line is L
0
: ax +by + c =0, and the equation of the circle
is C : (x − x
C
) + (y − y
C
) − r = 0, then the equations of the lines are
L
0
: −
b
√
a
2
+ b
2
x +
a
√
a
2
+ b
2
y +r +
b
√
a
2
+ b
2
C
x
−
a
√
a
2
+ b
2
C
y
= 0
L
1
:
b
√
a
2
+ b
2
x −
a
√
a
2
+ b
2
y +r −
b
√
a
2
+ b
2
C
x
+
a
√
a
2
+ b
2
C
y
= 0
C
r
P
1
P
2
2
1
0
Figure 8.34 Lines tangent to a given circle and normal to a given line.

8.16 Lines Tangent to a Given Circle and Normal to a Given Line 323
The pseudocode is
LinesTangentToCircleNormalToLine(Circle2D cir, Line2D l1, Line2D lOut[2])
{
float discrm = sqrt(l1.a * l1.a + l1.b * l1.b);
lOut[0].a = -l1.b / discrm;
lOut[0].b = l1.a / discrm;
lOut[0].c = cir.radius + ((b * cir.center.x) - (a * cir.center.y)) / discrm;
lOut[1].a = l1.b / discrm;
lOut[1].b = -l1.a / discrm;
lOut[1].c = cir.radius + ((-b * cir.center.x) + (a * cir.center.y)) / discrm;
}
If our line is given in normalized parametric form L(t) = P
0
+ t
ˆ
d, our two new
lines are simply
L
1
(t) = (C + r
ˆ
d) +t
ˆ
d
⊥
L
2
(t) = (C − r
ˆ
d) +t
ˆ
d
⊥
However, if L
0
is not normalized, we have
L
1
(t) =
C +r
d
d
+ t
ˆ
d
⊥
L
2
(t) =
C −r
d
d
+ t
d
⊥
The pseudocode is
LinesTangentToCircleNormalToLine(Circle2D cir, Line2D l1, Line2D lOut[2])
{
Vector2D dPerp;
dPerp.x = -l1.direction.y;
dPerp.y = l1.direction.x;
if (l1.isNormalized()) {
lOut[0].origin.x = cir.center.x + cir.radius * l1.direction.x;
lOut[0].origin.y = cir.center.y + cir.radius * l1.direction.y;
lOut[0].direction.x = dPerp.x;
lOut[0].direction.y = dPerp.y;
