Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

324 Chapter 8 Miscellaneous 2D Problems

lOut[1].origin.x = cir.center.x - cir.radius * l1.direction.x;

lOut[1].origin.y = cir.center.y - cir.radius * l1.direction.y;

lOut[1].direction.x = dPerp.x;

lOut[1].direction.y = dPerp.y;

} else {

float invLength = 1.0/l1.direction.length();

lOut[0].origin.x = cir.center.x + cir.radius * l1.direction.x * invLength;

lOut[0].origin.y = cir.center.y + cir.radius * l1.direction.y * invLength;

lOut[0].direction.x = dPerp.x;

lOut[0].direction.y = dPerp.y;

lOut[1].origin.x = cir.center.x - cir.radius * l1.direction.x * invLength;

lOut[1].origin.y = cir.center.y - cir.radius * l1.direction.y * invLength;

lOut[1].direction.x = dPerp.x;

lOut[1].direction.y = dPerp.y;

}

Chapter

9Geometric

Primitives in 3D

This chapter contains the deﬁnitions for various three-dimensional geometric prim-

itives that are commonly used in applications. Some of the primitives have multiple

representations. A geometric query involving an object might be more effectively for-

mulated with one representation than another. The discussion about a query will

indicate which representation is more appropriate.

In geometric queries with objects such as polyhedra, the object can be treated

as a two-dimensional or a three-dimensional object. For example, the tetrahedron

as a two-dimensional object is just the collection of four triangle faces. As a three-

dimensional object, the tetrahedron refers to its faces and the region that it bounds.

Some objects have distinct names for the two possibilities. For example, sphere refers

to the two-dimensional surface and ball refers to the sphere and the region it bounds.

When necessary, the distinction will be made clear. In the absence of distinct names,

the word solid will be used. For example, the method for computing the distance

between a point and a tetrahedron treats the tetrahedron as a solid. If a point is inside

the tetrahedron boundary, then the distance is zero.

9.1 Linear Components

The simplest form to work with for a line in 3D is the parametric form, X(t) =P +t



for t ∈ R, P a point on the line, and



d =



0 a direction for the line. A ray is a line

with the restriction on the parametric form that t ≥ 0. The origin of the ray is P .

A line segment, or simply segment, is a line with the restriction on the parametric

form that t ∈ [t

, t

]. I f P

and P

are end points of the segment, the standard form

325

326 Chapter 9 Geometric Primitives in 3D

for the segment is X(t) = (1 − t)P

+ tP

for t ∈ [0, 1]. This form is converted to

the parametric form by setting



d = P

− P

.Thesymmetric form for a segment

consists of a centerpoint C, a unit-length direction vector

d,andaradiusr.The

parameterization is X(t) = C + t

d for |t |≤r. The length of a segment is P

− P



for the standard form and 2r for the symmetric form.

Lines in 2D were equivalently deﬁned as the set of points satisfying the algebraic

equation n ·X =c,wheren =



0 is a normal vector to the line. The geometric analogy

in 3D is that a line is the set of intersection of two algebraic equations n

· X = c

and n

· X =c

,wheren

and n

are linearly independent. The two linear equations

have three unknowns, the components of X, so we expect that there is a single free

variable in the solution. This variable corresponds to the parameter of the line in the

parametric form. The formulation in terms of the intersection of two planes is called

the normal form for the line.

A parametric form for the line can be derived from the normal form. The cross

product n

×n

is perpendicular to both linearly independent vectors n

and n

so the three vectors form a linearly independent set. Any point can be written as a

linear combination of the vectors. In particular, P = d

n

+ d

n

+ t n

×n

. Deﬁne

=n

·n

. Taking dot products of the equation for P with the normal vectors, we

arrive at two equations c

=n

· P = e

+ e

and c

=n

· P = e

+ e

The two equations in the two unknowns d

and d

can be solved in the usual manner.

The parametric form for the line is

X(t) =

− e

n

− e

n

+ t n

×n

Throughout this book, the term linear component is used to denote a line, ray, or

segment.

9.2 Planar Components

Various deﬁnitions for planes are provided in this section. In many applications,

standard 2D objects are manipulated within a 3D environment. These objects must

be manipulated in a 3D coordinate system, even though they are naturally deﬁned in

a 2D coordinate system. The process of constructing the 3D representations of planar

2D objects is described here. Planes and any objects deﬁned in a plane are collectively

referred to as planar components.

9.2.1 Planes

A plane is deﬁned by the algebraic equation n ·(X −P)= 0, where n =



0isanormal

to the plane and where P is a point on the plane, as shown in Figure 9.1. This form

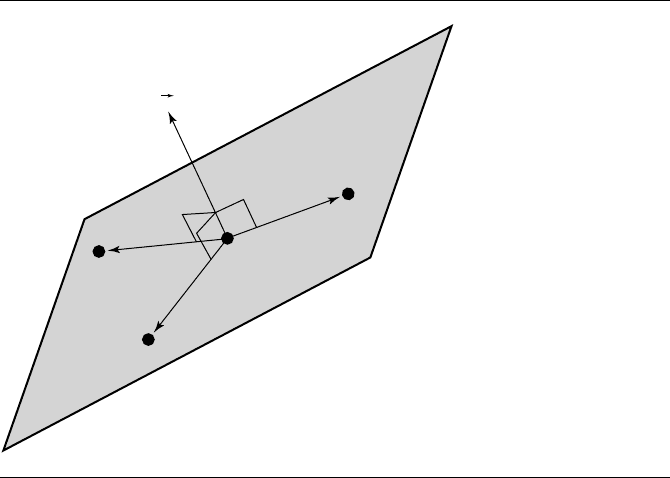
9.2 Planar Components 327

Figure 9.1 A plane is deﬁned as the set of all points X satisfying n · (X − P)= 0.

isreferredtoasthenormal-point form. A similar deﬁnition is n · X = c for some

constant c.Thisformisreferredtoasthenormal-constant form.Toconstructapoint

on the plane using the normal-constant form, choose P = d n for some scalar d.

Replacing this in the formula yields c =n · (d n) = dn

. Thus, d = c/n

. Going

in the other direction, given the normal-point form, the constant c in the normal-

constant form is c =n · P .

If we let X = [

xyz

], we can rewrite the vector X −P in terms of its com-

ponents, yielding

X − P =

[

x −P

y −P

z − P

]

If we let n = [

abc

], then we can rewrite the normal-point form of the plane

equation as

ax + by + cz + d = 0 (9.1)

where a, b, and c are constants, not all zero, and d =−n · P . This is known as the

implicit form of a plane equation—simply a slightly different rendering of the normal-

constant form—that is frequently seen in the literature.

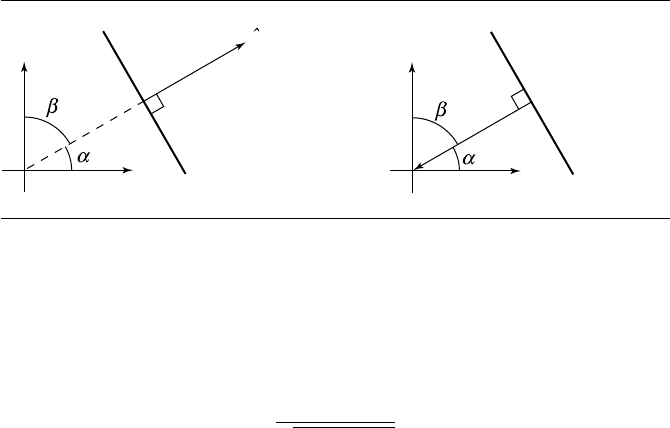
328 Chapter 9 Geometric Primitives in 3D

r = d

n = [a b c]

r = –d

Figure 9.2 Geometric interpretation of plane equation coefﬁcients.

If a

+ b

+ c

= 1 (or, equivalently, if n=1), then the plane equation is said

to be normalized. A nonnormalized representation can be converted by multiplying

the coefﬁcients through by

√

+ b

+ c

While it is not necessary, in the abstract, to use a normalized representation, many

algorithms involving planes can be made somewhat less computationally expensive

if a normalized representation is maintained; this is because the square root and

division can be done once “up front” and then avoided in various intersection or

distance computations.

The normalized form allows for a more intuitive geometric interpretation of

the coefﬁcients. Looking at Figure 9.2, we see a “cross section” of a plane that is

perpendicular to the page. Simple trigonometry shows us that

a =cos α

b = cos β

c = cos θ

where θ is the angle formed with the positive z-axis.

More signiﬁcantly (at least for intuition) is the following: if the distance from the

origin to the plane is r, then |d|=r; further, the sign of d is negative if ˆn points away

from the origin and positive if it points toward the origin.

The parametric form for a plane is X(s, t)=P +s ˆu +t ˆv for s ∈R and t ∈R.The

point P is on the plane. The directions ˆu =



0 and ˆv =



0 must be linearly independent

vectors (see Figure 9.3).

To convert from parametric form to normal-point form, just use P as the point

on the plane. The normal vector must be perpendicular to both direction vectors,

so ˆn =ˆu ×ˆv. To convert from normal-point form to parametric form, again use

P as is. We must choose two linearly independent vectors ˆu and ˆv that are perpen-

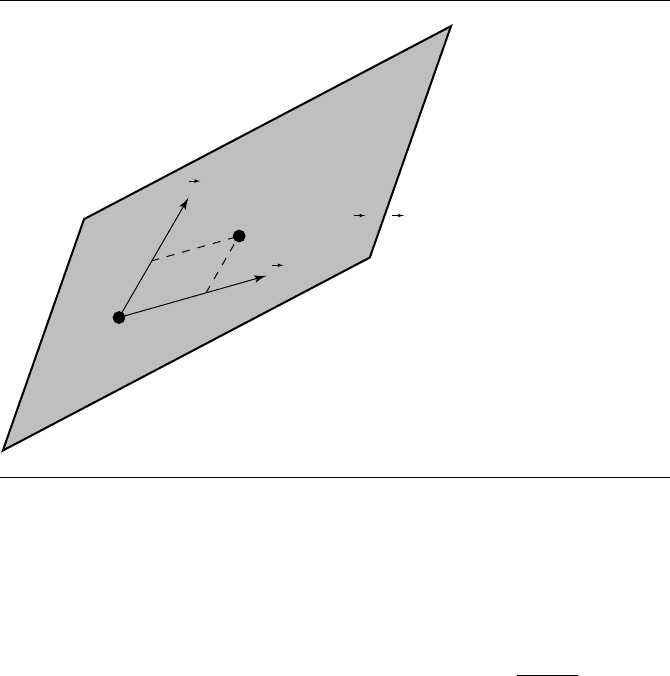
9.2 Planar Components 329

X(s, t) = P + su + tv

Figure 9.3 The parametric representation of a plane.

dicular to ˆn. There are inﬁnitely many choices, but here is one that allows a robust

numerical implementation. The idea is to choose a unit-length vector ˆu =(u

, u

)

perpendicular to ˆn = (n

, n

) so that ˆu has a zero component. You cannot safely

choose any component to be zero. For example, if you choose ˆu = (u

, u

,0), then

0 =n ·ˆu = n

. A formal solution is ˆu = (n

, −n

,0)/



+ n

, but clearly

there is an algebraic problem when n

= n

= 0 and numerical problems when n

and n

are both nearly zero. Better is to choose a component of ˆu to be zero based on

information about ˆn.

The pseudocode is

Vector N = nonzero plane normal;

Vector U, V;

if (|N.x| >= |N.y|) {

// N.x or N.z is the largest magnitude component, swap them

U.x = +N.z;

U.y=0;

U.z = -N.x;

} else {

330 Chapter 9 Geometric Primitives in 3D

// N.y or N.z is the largest magnitude component, swap them

U.x=0;

U.y = +N.z;

U.z = -N.y;

}

V = Cross(N, U);

9.2.2 Coordinate System Relative to a Plane

Given a plane with normal n and point P , sometimes it is convenient to have a full

orthonormal coordinate system for R

with origin at P , n as one of the coordinate

axis directions, and two other coordinate axes in the plane itself. In this case, n is ﬁrst

normalized so that it is a unit-length vector. The vector ˆu created in the pseudocode

of the last subsection is also normalized to unit length. The cross product ˆv =ˆn ×ˆu

is automatically unit length.

The pseudocode is

Vector N = unit-length plane normal;

Vector U, V;

if (|N.x| >= |N.y|) {

// N.x or N.z is the largest magnitude component

invLength=1/sqrt(N.x * N.x + N.z * N.z);

U.x = +N.z * invLength;

U.y=0;

U.z = -N.x * invLength;

} else {

// N.y or N.z is the largest magnitude component

invLength=1/sqrt(N.y * N.y + N.z * N.z);

U.x=0;

U.y = +N.z * invLength;

U.z = -N.y * invLength;

}

V = Cross(N, U); // automatically unit length

Any point X ∈R

can be written in the implied coordinate system as

X = P + y

ˆu + y

ˆv + y

ˆn = P + R y

where R is a rotation matrix whose columns are ˆu, ˆv, and ˆn (in that order) and where

y = (y

, y

) isa3× 1vector.

9.2 Planar Components 331

9.2.3 2D Objects in a Plane

Consider a set S ⊂R

in the xy-plane that represents a 2D object. Abstractly,

S ={(x, y) ∈ R

: (x, y) satisﬁes some constraints}

This object can be embedded in a 2D plane in 3D. Let the plane contain the point P

and have a unit-length normal ˆn.If ˆu and ˆv are vectors in the plane so that ˆu, ˆv, and

ˆn form an orthonormal set, then the (x, y) pairs for the object in 2D can be used as

the coordinates of ˆu and ˆv as a method for embedding the 2D object in the plane in

3D, the embedded set labeled S



⊂ R

. This set is deﬁned by



={P + x ˆu + y ˆv ∈R

: (x, y) ∈ S}

Observe that there are inﬁnitely many planes in which the 2D object can be em-

bedded. Within each plane there are inﬁnitely many ways to choose the vectors ˆu

and ˆv.

In many applications the problem is the reverse one—start with the object that

lives in a speciﬁc plane in 3D and obtain a congruent object in the xy-plane. The

term “congruent” refers to obtaining one object from the other by applying a rigid

motion. If S



is a set of points on a plane ˆn · (X −P)= 0, any point Q ∈ S



can be

converted to a point in the xy-plane by solving Q = P + x ˆu + y ˆv for x and y.Itis

assumed that {ˆu, ˆv, ˆn}is an orthonormal set. The solution is simple: x =ˆu · (Q −P)

and y =ˆv · (Q − P). Since Q is on the plane, ˆn · (Q − P)= 0. To see that the two

triangles are congruent, the three equations can be written in vector form as













ˆu · (Q − P)

ˆv · (Q − P)

ˆn · (Q − P)





= R(Q − P)

where R is a rotation matrix whose rows are ˆu, ˆv, and ˆn. Thus, points (x, y,0) in

the xy-plane are obtained from points in the plane ˆn · (X −P)= 0 by a translation

followed by a rotation, in total a rigid motion.

Example Given a 2D triangle with vertices (x

, y

) for i = 0, 1, 2, and given a plane ˆn · (X −

P)=0 in which the triangle should live, a simple choice for vertices of the triangle in

3D is V

= P + x

ˆu + y

ˆv for i = 0, 1, 2. Given vertices W

for i =0, 1, 2, construct

a triangle in the xy-plane that is congruent to the original triangle. To solve this

problem, construct a plane containing the original triangle. Deﬁne the plane origin

to be P = W

. Deﬁne the edge vectors e

= W

− W

and e

= W

− W

. A unit-

length normal vector to the plane of the triangle is ˆn =(e

×e

)/e

×e

. Construct

ˆu and ˆv as described earlier. Determine the coefﬁcients d

in the representations

e

ˆu +d

ˆv and e

ˆu +d

ˆv. The coefﬁcients are easily computed using dot

products, d

=e

·ˆu, d

=e

·ˆv, d

=e

·ˆu, and d

=e

·ˆv. The representations

lead to W

= W

+e

= P + d

ˆu + d

ˆv and W

= W

+e

= P + d

ˆu + d

ˆv.

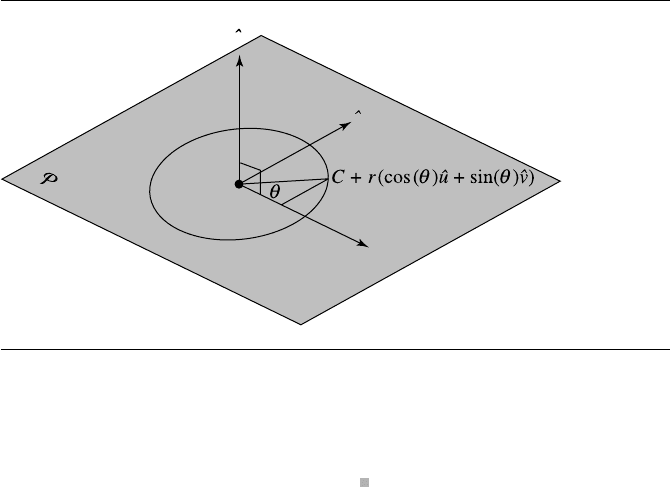
332 Chapter 9 Geometric Primitives in 3D

Figure 9.4 The parametric representation of a circle in 3D.

The vertices of the triangle as a 2D object are (0, 0), (d

, d

), and (d

, d

) and

correspond to W

, W

, and W

, respectively.

Example Suppose you want to have a formula for working with a circle in 3D whose center is

C ∈ R

and whose radius is r. The plane containing the circle is speciﬁed to have a

unit-length normal ˆn. The center of the circle must lie in the plane, so an equation

for the plane is ˆn · (X −C) = 0. The circle points X must be equidistant from the

center C, so another constraint is X − C=r. This algebraic equation deﬁned on

all of R

produces a sphere centered at C and of radius r. However, only points on

the plane are desired, so the circle can be viewed as the set of intersection of the plane

and sphere. In 2D, a circle centered at the origin and having radius r is parameterized

by x = r cos θ and y =r sin θ for θ ∈[0, 2π) (see Figure 5.15). Formally, the circle in

2D is the set S ={(r cos θ , r sin θ) ∈ R

: θ ∈ [0, 2π)}. In 3D, the circle embedded in

the plane is the set S



={C +(r cos θ)ˆu +(r sin θ)ˆv : θ ∈ [0, 2π)} (see Figure 9.4). If

we deﬁne a vector-valued function ˆw(θ) = cos θ ˆu + sin θ ˆv, then the parametric 3D

circle deﬁnition can be written more compactly as

P = C +r ˆw(θ)

It is simple to verify the constraints on X =C +(r cos θ)ˆu + (r sin θ)ˆv. First,

ˆn · (X −C) =ˆn · ((r cos θ)ˆu + (r sin θ)ˆv)

= (r cos θ)ˆn ·ˆu + (r sin θ)ˆn ·ˆv

= (r cos θ)0 +(r sin θ)0, ˆn is orthogonal to ˆu and ˆv

= 0

9.3 Polymeshes, Polyhedra, and Polytopes 333

Second,

X − C

=(r cos θ)ˆu + (r sin θ)ˆv

= (r

cos

θ)ˆu

+ (2r

sin θ cos θ)ˆu ·ˆv + (r

sin

θ)ˆv

= (r

cos

θ)1 + (2r

sin θ cos θ)0 +(r

sin

θ)1,

ˆu and ˆv are orthonormal

= r

cos

θ + r

sin

= r

Similar constructions apply to other quadratic curves in the plane.

Another quite useful method for obtaining a 2D representation of a planar object



in 3D is described below. The method uses projection, so the two objects are not

congruent. If the plane normal is ˆn = (n

, n

), and if n

= 0, the projection of

a point Q = (q

, q

) ∈ S



onto the xy-plane is Q



= (q

, q

). The condition that

= 0 is important. If it were zero, the plane of the object projects onto a straight

line, thereby losing much information about the original object. If in fact n

=0, the

projection can be made onto the xz-plane if n

=0 or onto the yz-plane if n

=0. In

practice, the largest magnitude normal component is used to identify the coordinate

plane of projection. This makes the projected object as large as possible compared to

its projections on the other coordinate planes. A typical application where this type

of construction is useful is in triangulation of a planar polygon in 3D. The congruent

mapping requires computing (x, y) = ( ˆu · (Q − P), ˆv · (Q − P)) for all polygon

vertices Q. The difference Q − P requires 3 subtractions, and each dot product

requires 2 multiplications and 1 addition. The total operation count for n vertices

is 9n. The projection mapping requires identifying a nonzero normal component

and extracting the two components for the coordinate plane of projection. Finding

the normal component is the only computational expense and requires a couple

of ﬂoating-point comparisons, clearly much cheaper than the congruent mapping.

The triangulation in the xy-plane produces triples of vertex indices that represent

the triangles. These triples are just as valid for the original polygon in 3D. Another

application is in computing the area of a planar polygon in 3D; Section 13.12 has

more detail on the construction.

9.3 Polymeshes, Polyhedra, and Polytopes

In this section are deﬁnitions for objects that consist of three types of geometric

components: vertices, edges, and faces. Vertices are, of course, just single points.

Edges are line segments whose end points are vertices. Faces are convex polygons

that live in 3D. Many applications support only triangular faces because of their

simplicity in storage and their ease of use in operations applied to collections of