Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

334 Chapter 9 Geometric Primitives in 3D

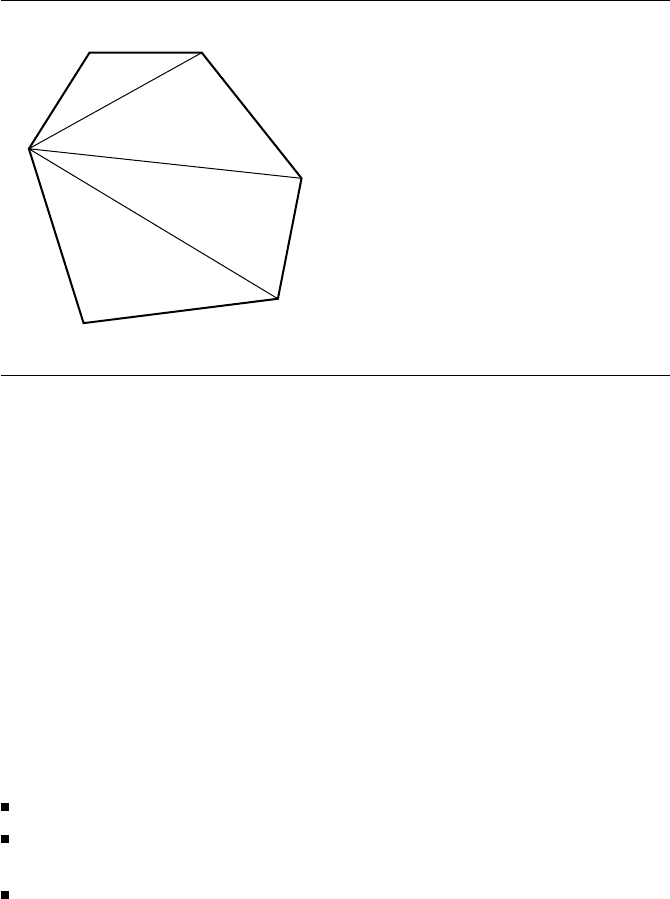
Figure 9.5 A convex polygon and its decomposition into a triangle fan.

the faces. It is possible to allow nonconvex polygon faces, but this only complicates

the implementation and manipulation of the objects. If triangles are required by an

application and the faces are convex polygons, the faces can be fanned into triangles.

If the n vertices of the face are ordered as V

through V

n−1

, the n − 2 triangles whose

union is the face are V

, V

i+1

 for 1 ≤ i ≤ n − 2. Figure 9.5 shows a convex face

and its decomposition into a triangle fan. If a face is a simple polygon that is not

convex, it can be decomposed into triangles by any of the triangulation methods

discussed in Section 13.9. Figure 9.6 shows a nonconvex face and its decomposition

into triangles. Triangulation is generally an expense that an application using meshes

should not have to deal with at run time; hence the common restriction that the faces

be triangles themselves or, in the worst case, convex polygons.

A ﬁnite collection of vertices, edges, and faces is called a polygonal mesh,orin

short a polymesh, as long as the components satisfy the following conditions:

Each vertex must be shared by at least one edge. (No isolated vertices are allowed.)

Each edge must be shared by at least one face. (No isolated edges or polylines

allowed.)

If two faces intersect, the vertex or edge of intersection must be a component in

the mesh. (No interpenetration of faces is allowed. An edge of one face may not

live in the interior of another face.)

If all the faces are triangles, the object is called a triangle mesh, or in short a trimesh.

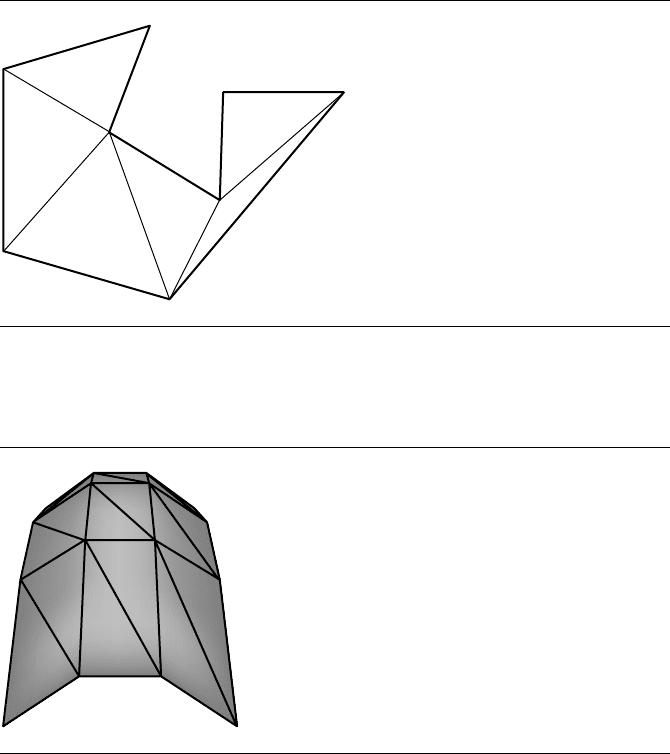
Figure 9.7 shows a triangle mesh. Figure 9.8 shows a collection of vertices, edges,

and triangles that fails the ﬁrst condition—a vertex is isolated and not used by a

triangle. Figure 9.9 shows a collection of vertices, edges, and triangles that fails the

9.3 Polymeshes, Polyhedra, and Polytopes 335

Figure 9.6 A nonconvex polygon and its decomposition into triangles.

Figure 9.7 A triangle mesh.

second condition—an edge is not an edge of the triangle, even though an end point

is a vertex of a triangle. Figure 9.10 shows a collection of vertices, edges, and triangles

that fails the third condition—two triangles are interpenetrating, so they intersect at

some points that are not in the original collection of vertices, edges, and triangles.

A polyhedron (plural: polyhedra) is a polymesh that has additional constraints.

The intuitive idea is that a polyhedron encloses a bounded region of space and that

it has no unnecessary edge junctions. The simplest example is a tetrahedron,apoly-

mesh that has four vertices, six edges, and four triangular faces. The standard tetra-

hedron has vertices V

= (0, 0, 0), V

= (1, 0, 0), V

= (0, 1, 0), and V

= (0, 0, 1).

336 Chapter 9 Geometric Primitives in 3D

Figure 9.8 Vertices, edges, and triangles are not a mesh since a vertex is isolated.

Figure 9.9

Vertices, edges, and triangles are not a mesh since an edge is isolated.

The edges are E

=V

, V

, E

=V

, V

, E

=V

, V

, E

=V

, V

, E

V

, V

, and E

=V

, V

. The faces are T

012

=V

, V

, T

013

=V

, V

,

023

=V

, V

, and T

123

=V

, V

. The additional constraints for a polymesh

to be a polyhedron are as follows:

The mesh is connected when viewed as a graph whose nodes are the faces and

whose arcs are the edges shared by adjacent faces. Intuitively, a mesh is connected

if you can reach a destination face from any source face by following a path of

pairwise adjacent faces from the source to the destination.

9.3 Polymeshes, Polyhedra, and Polytopes 337

Figure 9.10 Vertices, edges, and triangles are not a mesh since two triangles interpenetrate.

Each edge is shared by exactly two faces. This condition forces the mesh to be a

closed and bounded surface.

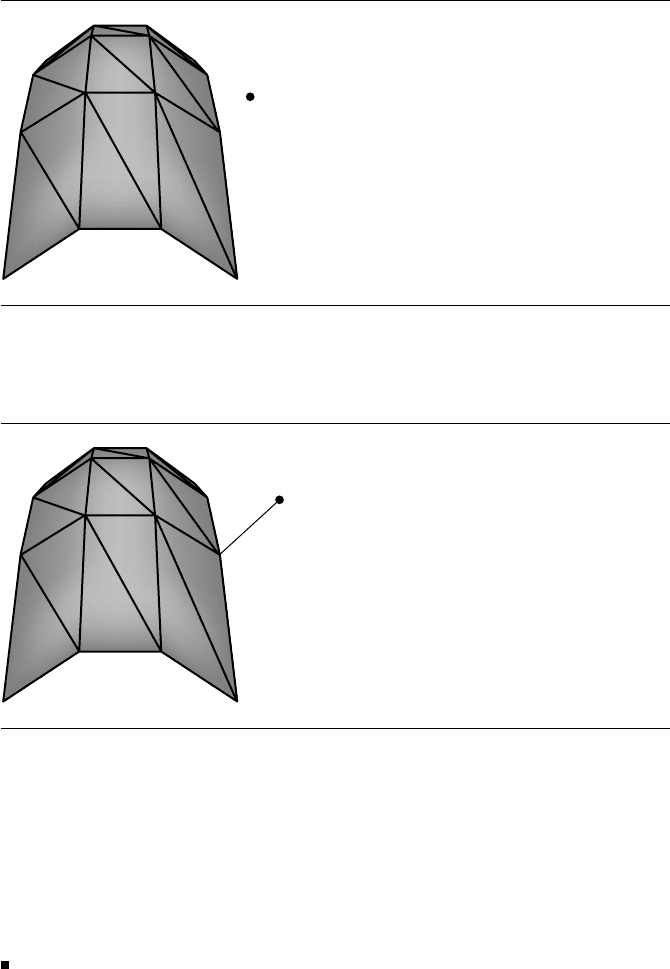
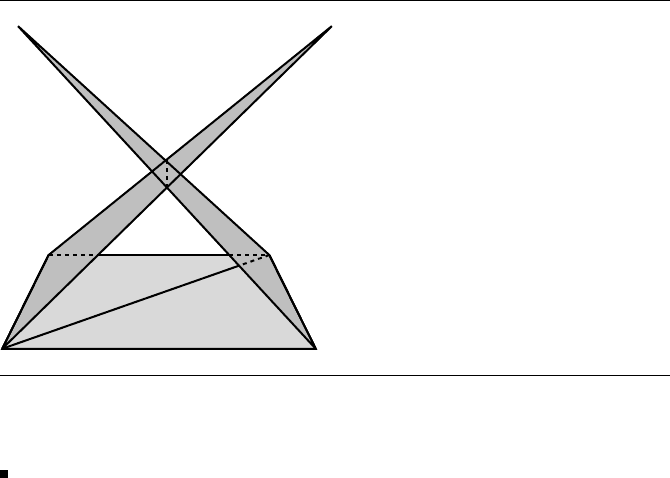
Figure 9.11 shows a polyhedron. Figure 9.12 is a polymesh, but not a polyhedron

since it is not connected. Observe that the tetrahedron and the rectangle mesh share

a vertex, but the connectivity has to do with triangles sharing edges, not sharing

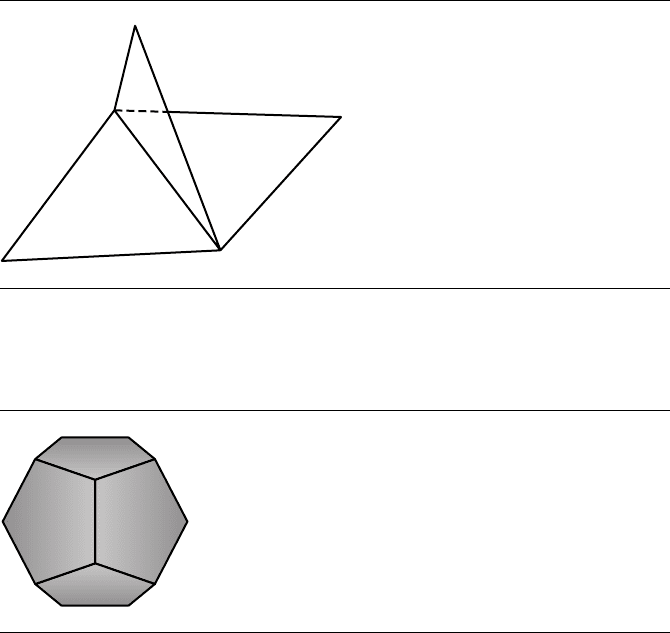
singleton vertices. Figure 9.13 is a polymesh, but not a polyhedron since an edge is

shared by three faces.

A polytope is a polyhedron that encloses a convex region R. That is, given any two

points X and Y in R, the line segment (1 − t)X + tY is also in R for any t ∈ [0, 1].

Figure 9.14 shows a polytope.

9.3.1 Vertex-Edge-Face Tables

An implementation of a polymesh requires some type of data structure for represent-

ing the components and their adjacencies. A simple data structure is a vertex-edge-face

table.TheN unique vertices are stored in an array,

Vertex[0] through Vertex[N-1],

so vertices can be referred to by their indices into the array.

Edges are represented by pairs of vertex indices, and faces are represented by

ordered lists of vertex indices. The table is deﬁned by the grammar:

VertexIndex = 0 throughN-1;

VertexIndexList = EMPTY or { VertexIndex V; VertexIndexList VList; }

EdgeList = EMPTY or { Edge E; EdgeList EList; }

338 Chapter 9 Geometric Primitives in 3D

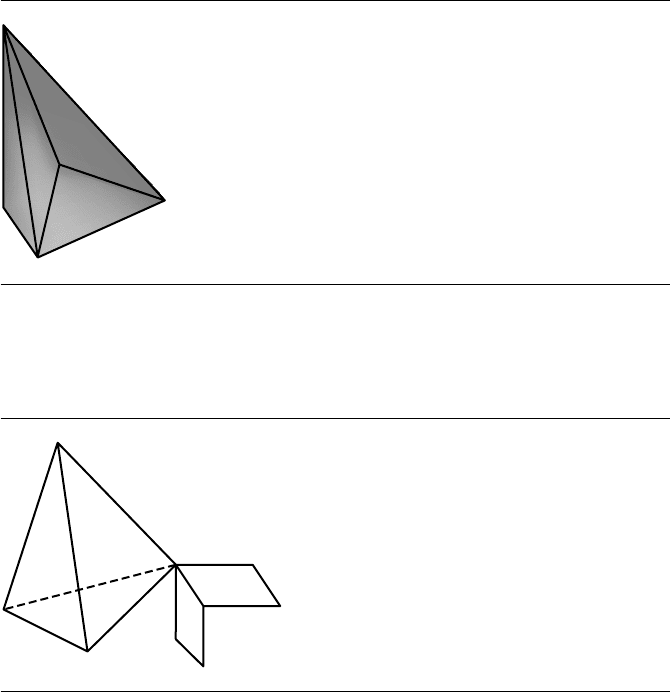
Figure 9.11 A polyhedron that consists of a tetrahedron, but an additional vertex was added to

form a depression in the centered face.

Figure 9.12 A polymesh that is not a polyhedron since it is not connected. The fact that the tetra-

hedron and rectangle mesh share a common vertex does not make them connected

in the sense of edge-triangle connectivity.

FaceList = EMPTY or { Face F; FaceList FList; }

Vertex = { VertexIndex V; EdgeList EList; FaceList FList; }

Edge = { VertexIndex V[2]; FaceList FList; }

Face = { VertexIndexList VList; }

The edge list EList in the Vertex object is a list of all edges that have an end point

corresponding to the vertex indexed by

V. The face list FList in the Vertex object is a

list of all faces that have a vertex corresponding to the vertex indexed by

V. The face

list

FList in the Edge object is a list of all faces that share the speciﬁed edge. An Edge

object does not directly know about edges sharing either of its vertices. A Face object

9.3 Polymeshes, Polyhedra, and Polytopes 339

Figure 9.13 A polymesh that is not a polyhedron since an edge is shared by three faces.

Figure 9.14 A polytope, a regular dodecahedron.

does not know about vertices or edges that share the face’s vertices. This information

can be indirectly obtained by various queries applied to the subobjects of either

Edge

or Face.

By the deﬁnition of a polymesh, the face list in

Edge cannot be empty since any

edge in the collection must be part of at least one face in the collection. Similarly, the

edge and face lists in

Vertex must both be nonempty. If both were empty, the vertex

would be isolated. If the edge list were not empty and the face list were empty, the

vertex would be part of an isolated polyline, and the immediately adjacent edges have

no faces containing them.

The edges can be classiﬁed according to the number of faces sharing them. An

edge is a boundary edge if it has exactly one face using it. Otherwise, the edge is an

interior edge. If an interior edge has exactly two faces sharing it, it is called a manifold

edge. All edges of a polyhedron are required to be of this type. If an interior edge has

three or more faces sharing it, it is called a junction edge.

340 Chapter 9 Geometric Primitives in 3D

9.3.2 Connected Meshes

A direct application of depth-ﬁrst search to the mesh allows us to construct the

connected components of the mesh. Initially all faces are marked as unvisited. Starting

with an unvisited face, the face is marked as visited. For each unvisited face adjacent

to the initial face, a traversal is made to that face and the process is applied recursively.

When all adjacent faces of the initial face have been traversed, a check is made on all

faces to see if they have all been visited. If so, the mesh is said to be connected. If not,

the mesh has multiple connected submeshes, each called a connected component.

Each of the remaining components can be found by starting a recursive traversal with

any unvisited face. The pseudocode below illustrates the process, but with a stack-

based approach rather than one using a recursive function call.

MeshList GetComponents(Mesh mesh)

{

MeshList componentList;

// initially all faces are unvisited

Face f;

for (each face f in mesh)

f.visited = false;

// find the connected component of an unvisited face

while (mesh.HasUnvisitedFaces()) {

Stack faceStack;

f = mesh.GetUnvisitedFace();

faceStack.Push(f);

f.visited = true;

// traverse the connected component of the starting face

Mesh component;

while (not faceStack.empty()) {

// start at the current face

faceStack.Pop(f);

component.InsertFace(f);

for(inti=0;i<f.numEdges; i++) {

// visit faces sharing an edge of f

Edge e = f.edge[i];

// visit each adjacent face

for(intj=0;j<e.numFaces; j++) {

Face a = e.face[j];

if (not a.visited) {

9.3 Polymeshes, Polyhedra, and Polytopes 341

// this face not yet visited

faceStack.Push(a);

a.visited = true;

}

componentList.Insert(component);

}

return componentList;

}

If all that is required is determining if a mesh is connected, the following pseu-

docode is a minor variation of the previous code that does the trick:

bool IsConnected(Mesh mesh)

{

// initially all faces are unvisited

Face f;

for (each face f in mesh)

f.visited = false;

// start the traversal at any face

Stack faceStack;

f = mesh.GetUnvisitedFace();

faceStack.Push(f);

f.visited = true;

while (not faceStack.empty()) {

// start at the current face

faceStack.Pop(f);

for(inti=0;i<f.numEdges; i++) {

// visit faces sharing an edge of f

Edge e = f.edge[i];

// visit each adjacent face

for(intj=0;j<e.numFaces; j++) {

Face a = e.face[j];

if (not a.visited) {

// this face not yet visited

faceStack.Push(a);

a.visited = true;

}

342 Chapter 9 Geometric Primitives in 3D

}

// check if any face has not been visited

for (each face f in mesh) {

if (f.visited == false)

return false;

}

// all faces were visited, the mesh is connected

return true;

}

9.3.3 Manifold Meshes

A connected mesh is said to be a manifold mesh if each edge in the mesh is shared

by at most two faces. The topology of manifold face meshes is potentially more com-

plicated than for meshes in the plane. The problem is one of orientability. Although

there is a formal mathematical deﬁnition for orientable surfaces, we will use a deﬁni-

tion for manifold meshes that hints at a test itself for orientability. A manifold mesh

is orientable if the vertex orderings for the faces can be chosen so that adjacent faces

have consistent orderings.LetF

and F

be adjacent faces sharing the edge V

, V

.If

and V

occur in this order for F

, then they must occur in F

in the order V

fol-

lowed by V

. The prototypical case is for a mesh of two triangles that share an edge.

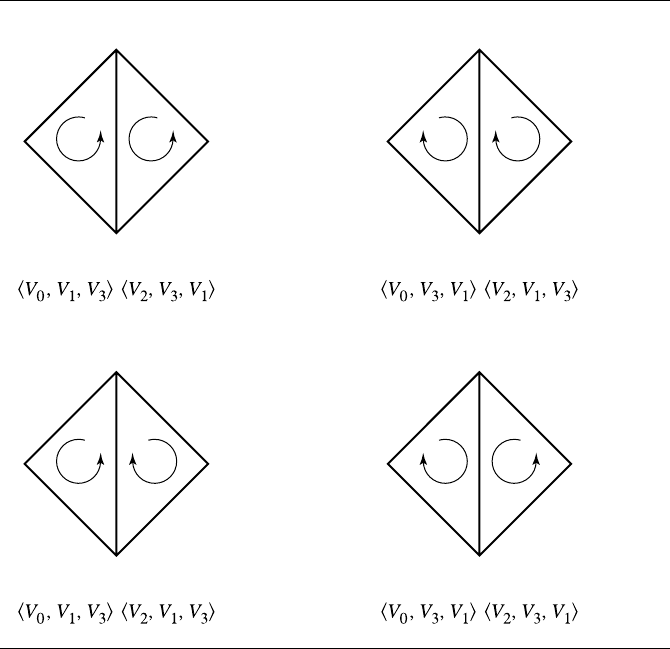
Figure 9.15 shows the four possible conﬁgurations.

obius strip is an example of a nonorientable surface. Figure 9.16 shows this.

Two parallel edges of a rectangle in 3D can be joined together to form a cylindrical

strip that is orientable. However, if the rectangle is twisted so that the edges join in

reversed order, a M

obius strip is obtained, a nonorientable surface.

In nearly all graphics applications, meshes are required to be orientable. Observe

that the deﬁnition for manifold mesh is topological in the sense that only vertex or-

derings and connectivity information are mentioned in the deﬁnition, not vertex,

edge, or face locations. The deﬁnition does not rule out self-intersections, a geomet-

rical property. Usually applications also require a mesh to be non-self-intersecting.

9.3.4 Closed Meshes

A connected mesh is said to be a closed mesh if it is manifold with each edge shared by

exactly two faces and is non-self-intersecting. The typical example of a closed mesh

is a triangle mesh that tessellates a sphere. If a mesh is not closed, it is said to be an

open mesh. For example, a triangle mesh that tessellates a hemisphere is open.

9.3 Polymeshes, Polyhedra, and Polytopes 343

Consistent

orderings

Inconsistent

orderings

Figure 9.15 The four possible conﬁgurations for ordering of two adjacent triangles.

9.3.5 Consistent Ordering

The condition of orientability for a manifold mesh is very important in computer

graphics applications. By implication, a manifold mesh has two consistent orderings

of its faces. Each ordering provides a set of face normals. In the two-triangle example

of Figure 9.15, an open manifold mesh, the top images show the two consistent

orderings for the mesh. The normal vectors for the ordering on the left are n

− V

) × (V

− V

) and n

= (V

− V

) × (V

− V

). Both normals point out of

the plane of the page of the image. The normal vectors for the ordering on the right

are just −n

and −n

. Generally, the set of normal vectors for one consistent ordering

of a mesh is obtained from the set of normal vectors for the other consistent ordering

by negating all the normals from the ﬁrst set.