Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

354 Chapter 9 Geometric Primitives in 3D

Intersecting planes

–

Hyperbolic cylinder

–

–1

Elliptic paraboloid

Elliptic cylinder

Hyperbolic paraboloid

–

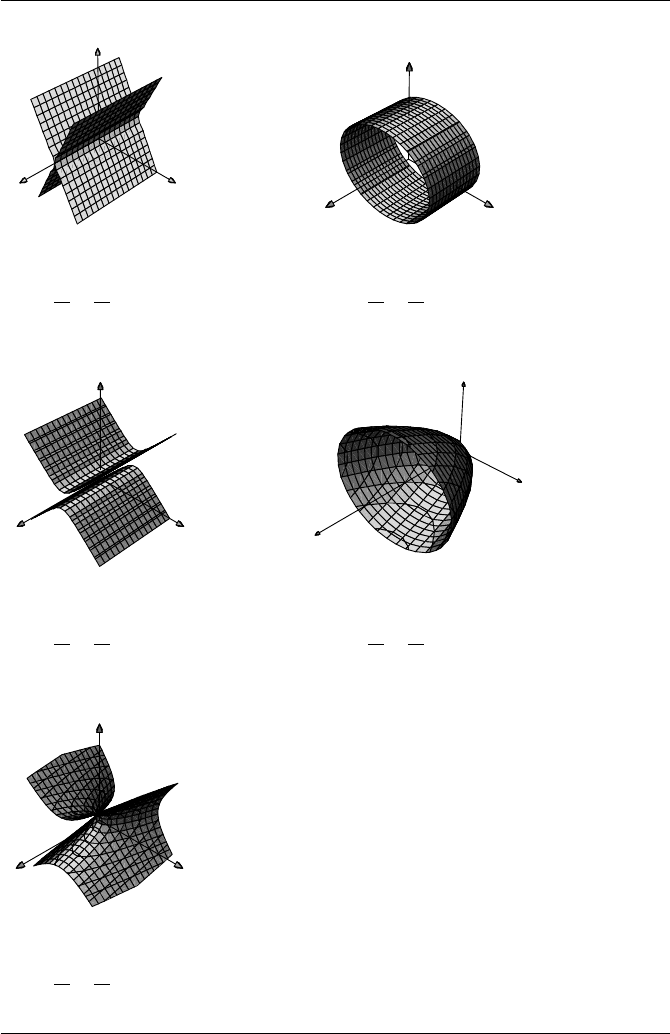
Figure 9.19 Quadrics having two nonzero eigenvalues.

9.5 Torus 355

Parallel planes

= a

Parabolic cylinder

+ 2rz = 0

Figure 9.20 Quadrics having one nonzero eigenvalue.

Figure 9.21 A standard “ring” torus.

9.5 Torus

A torus in 3D is a quartic (degree 4) surface, having (in its most common range of

proportions) the shape commonly known as a “doughnut,” as shown in Figure 9.21.

A torus may be considered to be deﬁned by rotating a circle about an axis lying in

the plane of the circle, or by taking a rectangular sheet and pasting the opposite edges

together (so that no twists form). Several alternative representations are possible: two

different implicit deﬁnitions

356 Chapter 9 Geometric Primitives in 3D

+ y

+ z

+ x

+ 2x

+ 2y

− 2(r

+ r

+ 2(r

− r

− 2(r

+ r

+ (r

− r

)

= 0

and

−



+ y

)

+ z

= r

and a parametric deﬁnition

x = (r

+ r

cos v) cos u

y = (r

+ r

cos v) sin u

z = r

sin v

where r

is the radius from the center of the torus to the center of the “tube” of the

torus (the major radius) and r

is the radius of the “tube” itself (the minor radius).

Generally, the major radius is greater than the minor radius (r

); this corre-

sponds to a ring torus, one of the three standard tori; the other two are the horn torus

= r

) and the self-intersecting spindle torus (r

) (Weisstein 1999).

The surface area S and volume V of a ring torus can be easily computed (Weis-

stein 1999). Recalling that the circumference and area of a circle with radius r are 2πr

and πr

, respectively, and that a torus can be considered to be the surface resulting

from rotating a circle around an axis parallel to the plane in which it lies, it can be

seen directly that

S = (2πr

)(2πr

)

= 4π

and

V = (2πr

)(2πr

)

= 2π

9.6 Polynomial Curves

A polynomial curve in space is a vector-valued function X : D ⊂ R → R ⊂ R

,say,

X(t), and has domain D and range R. The components X

(t) of X(t) areeacha

polynomial in the speciﬁed parameter

(t) =



j=0

9.6 Polynomial Curves 357

where n

is the degree of the polynomial. In most applications the degrees of the

components are the same, in which case the curve is written as X(t) =



j=0

for known points A

∈ R

. The domain D is typically either R or [0, 1]. A rational

polynomial curve is a vector-valued function X(t) whose components X

(t) are ratios

of polynomials

(t) =



j=0



j=0

where n

and m

are the degrees of the numerator and denominator polynomials.

A few common types of curves that occur in computer graphics are B

ezier curves,

B-spline curves, and nonuniform rational B-spline (NURBS) curves. Only the deﬁ-

nitions for these curves are given here. Various properties of interest may be found

in other texts (Bartels, Beatty, and Barsky 1987; Cohen, Riesenfeld, and Elber 2001;

Farin 1990, 1995; Rogers 2001; Yamaguchi 1988).

9.6.1 B

ezier Curves

A spatial B´ezier curve is constructed from a set of points P

∈R

for 0 ≤i ≤ n, called

control points,by

X(t) =



i=0





(1 − t)

n−1



i=0

(t)P

where t ∈ [0, 1]. The real-valued polynomials B

(t) are called the Bernstein polyno-

mials, each of degree n. The polynomial components of X(t) are therefore also of

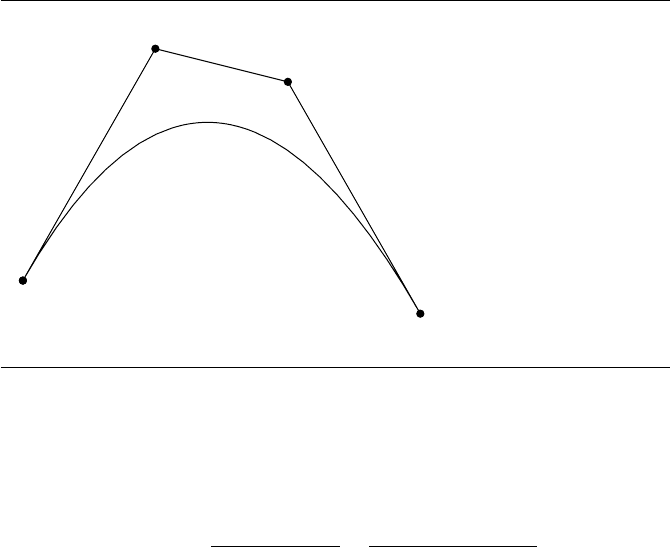
degree n. Figure 9.22 shows a cubic B

ezier curve, along with the control points and

control polygon.

9.6.2 B-Spline Curves

A spatial B-spline curve of degree j is constructed from a set of points P

∈ R

, called

control points, and a monotone set of parameters t

(i.e., t

≤ t

i+1

), called knots, for

0 ≤i ≤ n,by

X(t) =



i=0

i,j

(t)P

where t ∈[t

, t

]and 1 ≤j ≤n.Thevector(t

, ..., t

) is called a knot vector. The real-

valued polynomials B

i,j

(t) areofdegreej and deﬁned by the Cox–de Boor recursion

formulas

358 Chapter 9 Geometric Primitives in 3D

Figure 9.22 A cubic B

ezier curve.

i,0

(t) =



1, t

≤ t<t

i+1

0, otherwise

i,j

(t) =

(t − t

i,j −1

(t)

i+j −1

− t

i+j

− t)B

i+1,j −1

(t)

i+j

− t

i+1

for 1 ≤ j ≤ n. The polynomial components of X(t) are actually deﬁned piecewise

on the intervals [t

, t

i+1

]. On each interval the polynomial is of degree j. The knot

values are not required to be evenly spaced. In this case the curve is said to be a

nonuniform B-spline curve. If the knot values are equally spaced, then the curve is

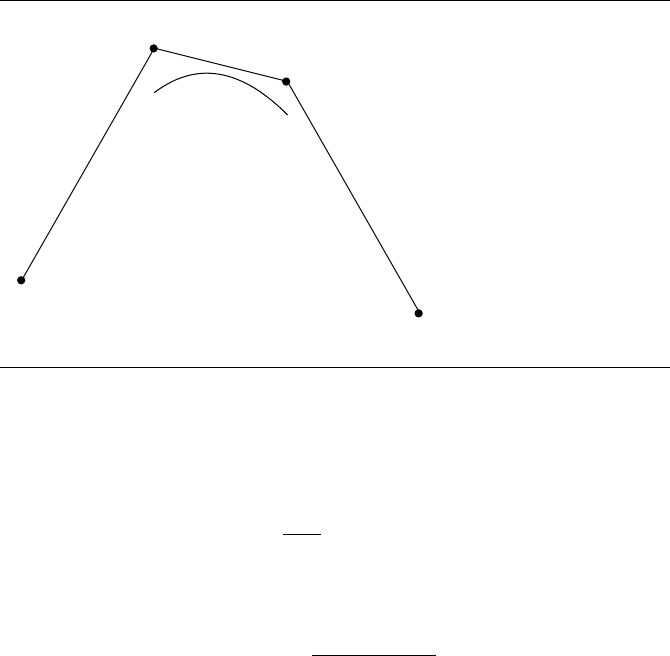
called a uniform B-spline curve. Figure 9.23 shows a uniform cubic B-spline curve,

along with the control points and control polygon.

9.6.3 NURBS Curves

A spatial nonuniform rational B-spline curve or NURBS curve is obtained from a

nonuniform B-spline polynomial curve in three dimensions. The control points are

,1) ∈ R

for 0 ≤ i ≤ n, with weights w

> 0, and the polynomial curve is

(Y (t ), w(t)) =



i=0

i,j

(t)w

,1)

where B

i,j

(t) is the same polynomial deﬁned in the previous subsection. The NURBS

curve is obtained by treating (Y (t), w(t)) as a homogeneous vector and dividing

9.7 Polynomial Surfaces 359

Figure 9.23 A cubic B-spline curve.

through by the last component to obtain a projection in three dimensions

X(t) =

Y(t)

w(t)



i=0

i,j

(t)P

where

i,j

(t) =

i,j

(t)



i=0

i,j

(t)

9.7

Polynomial Surfaces

A polynomial surface is a vector-valued function X : D ⊂ R

→ R

,say,X(s, t),

whose domain is D and range is R. The components X

(s, t) of X(s, t) areeacha

polynomial in the speciﬁed parameters

(s, t) =



j=0



k=0

ij k

where n

+ m

is the degree of the polynomial. The domain D is typically either R

or [0, 1]

.Arational polynomial surface is a vector-valued function X(s, t) whose

components X

(s, t) are ratios of polynomials

360 Chapter 9 Geometric Primitives in 3D

(s, t) =



j=0



k=0

ij k



j=0



k=0

ij k

where n

is the degree of the numerator polynomial and p

is the degree of

the denominator polynomial.

A few common types of surfaces that occur in computer graphics are B

ezier

surfaces, B-spline surfaces, and nonuniform rational B-spline (NURBS) surfaces.

Only the deﬁnitions for these surfaces are given here. Various properties of interest

may be found in other texts (Bartels, Beatty, and Barsky 1987; Cohen, Riesenfeld, and

Elber 2001; Farin 1990, 1995; Rogers 2001; Yamaguchi 1988).

9.7.1 B

ezier Surfaces

ThetwotypesofsurfacesdeﬁnedhereareB

ezier rectangle patches and B

ezier triangle

patches.

ezier Rectangle Patches

Given a rectangular lattice of three-dimensional control points P

for 0 ≤i

≤ n

and 0 ≤i

≤ n

, the B

ezier rectangle patch for the points is

X(s, t) =



(s)B

(t) P

, (s, t) ∈ [0, 1]

where





i!(n − i)!

is the number of combinations of i items chosen from a set of n items. The coefﬁcients

are products of the Bernstein polynomials

n,i

(z) =





(1 − z)

n−i

The patch is called a rectangle patch because the domain [0, 1]

is a rectangle in the

st-plane. Figure 9.24 shows a bicubic B

ezier surface, along with the control points

and control polygon.

9.7 Polynomial Surfaces 361

Figure 9.24 A bicubic B

ezier surface.

ezier Triangle Patches

Given a triangle lattice of three-dimensional control points P

for i

≥ 0, i

≥ 0,

≥ 0, and i

+ i

= n, the B

ezier triangle patch for the points is

X(u, v, w) =



|I |=n

n,I

(u, v, w) P

where I =(i

, i

), |I |=i

, u ≥0, v ≥0, w ≥0, and u +v +w =1. The

summation involves (n + 1)(n + 2)/2 terms. The Bernstein polynomial coefﬁcients

are

n,I

(u, v, w) =



, i



Although the patch has three variables u, v, and w, the fact that w =1 − u − v

really shows that X depends only on u and v. The patch is called a triangle patch

because the domain u ≥ 0, v ≥0, w ≥0, and u + v +w =1 is an equilateral triangle

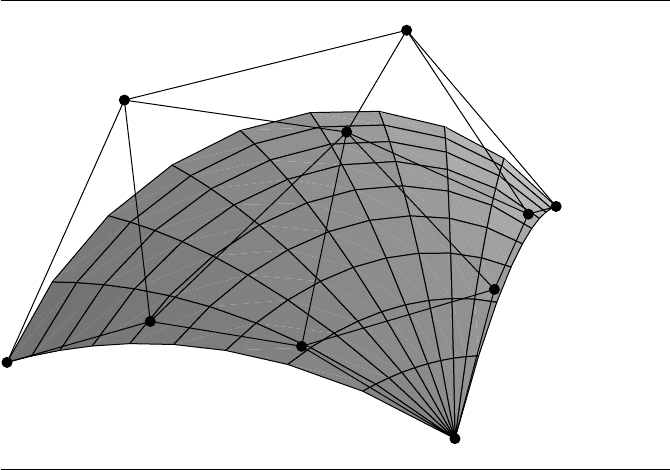
362 Chapter 9 Geometric Primitives in 3D

Figure 9.25 A cubic triangular B

ezier surface.

in uvw-space with vertices at (1, 0, 0), (0, 1, 0), and (0, 0, 1). Figure 9.25 shows a cubic

triangular B

ezier surface, along with the control points and control polygon.

9.7.2 B-Spline Surfaces

We only consider one type of B-spline surface, a B-spline rectangle patch. The concept

of B-spline triangle patches does exist (Dahmen, Micchelli, and Seidel 1992), but is

not considered in this book.

Let {s

}

i=0

be a monotone set, that is, s

≤ s

i+1

for all i. The elements are called

knots, and the vector (s

, ..., s

) is called a knot vector. Similarly, let {t

}

i=0

a monotone set using the same terminology. Given a rectangular lattice of three-

dimensional control points P

for 0 ≤ i

≤ n

and 0 ≤ i

≤ n

, a B-spline rectangle

patch is

X(s, t) =



(0)

(s)B

(1)

(t) P

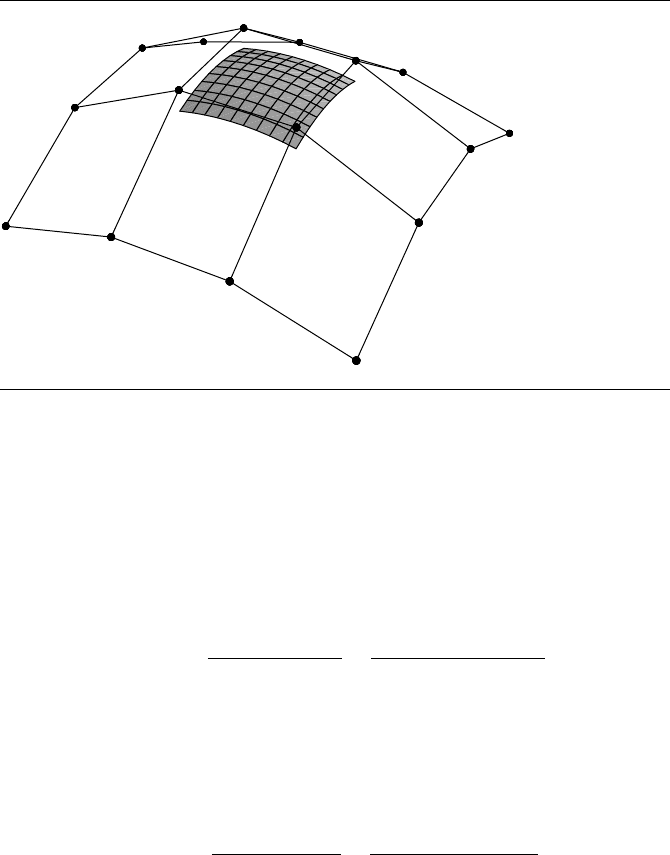
9.7 Polynomial Surfaces 363

Figure 9.26 A uniform bicubic B-spline surface.

where s ∈ [s

, s

], t ∈ [t

, t

], 1 ≤ j

≤ n

,1≤ j

≤ n

, and the polynomials in the

expression satisfy the Cox–de Boor formulas

(0)

i,0

(s) =



1, s

≤ s<s

i+1

0, otherwise

(0)

i,j

(s) =

(s − s

(0)

i,j −1

(s)

i+j −1

− s

i+j

− s)B

(0)

i+1,j −1

(s)

i+j

− s

i+1

and

(1)

i,0

(t) =



1, t

≤ t<t

i+1

0, otherwise

(1)

i,j

(t) =

(t − t

(1)

i,j −1

(t)

i+j −1

− t

i+j

− t)B

(1)

i+1,j −1

(t)

i+j

− t

i+1

The polynomial components of X(s, t) are actually deﬁned piecewise on the sets

, s

i+1

] × [t

, t

j+1

]. On each such set the polynomial is of degree i + j . The knot

values are not required to be evenly spaced. In this case the surface is said to be a

nonuniform B-spline surface. If the knot values are equally spaced, then the surface

is called a uniform B-spline surface. Figure 9.26 shows a uniform bicubic B-spline

surface, along with the control points and control polygon.