Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

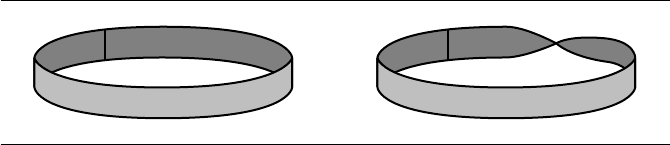
344 Chapter 9 Geometric Primitives in 3D
(a) (b)
Figure 9.16 A rectangle has two parallel edges joined together forming (a) a cylindrical strip
(orientable) or (b) a M
¨
obius strip (nonorientable).
An application has to decide which of the two consistent orderings it will use
for meshes. The typical choice is based on visibility of the mesh from an eye point
(camera location). The ordering is chosen so that mesh faces that are visible (ignoring
self-occlusion for the sake of the argument) have normal vectors that are directed
toward the eye point. That is, if a mesh face is in a plane n · (X −P)= 0, and if the
eye point is E, the face is visible when n · (E −P)>0. Such faces are said to be front-
facing. The vertices, when viewed from the eye point, are counterclockwise ordered
in the plane of the face. The faces for which n · (E − P)≤ 0 are said to be back-
facing. In a standard graphics rendering system, back-facing faces can be discarded
immediately and not transformed or lit, thereby saving a lot of time in rendering.
For a scene with a lot of closed meshes, the intuition is that approximately half of the
faces are back-facing. Not drawing them leads to a signicant increase in performance.
Using the same convention for selecting the consistent ordering, the normals of a
closed mesh point outside the region bounded by the mesh. This is important for
visibility and lighting as mentioned earlier, but it is also important for geometric
queries. For example, a point-in-polytope query might depend on the fact that all
normals are outward pointing. Of course, if all normals are inward pointing, the test
can still be correctly implemented. What is important is that a consistent ordering be
chosen and the various systems that manipulate meshes adhere to that ordering.
Toward that goal, sometimes applications can construct a connected manifold
mesh that is orientable, but the face orderings are not consistent. The classic exam-
ple is extraction of a level surface from a 3D voxel data set as a mesh of triangles.
Each voxel is processed independently of the others, and a collection of triangles that
approximate the level surface is constructed. The triangles are specified as triples of
indices into an array of vertices that lie on the level surface. The full set of triangles
forms an orientable mesh (level surfaces are always orientable), but the triangle or-
derings might not be consistent because of the independent processing. It is desirable
to reorder some of the triples of indices to produce a consistent ordering for the mesh.
If the mesh is stored in a vertex-edge-face table, a depth-first search of the abstract
graph represented by the table can be used to obtain the consistency. An initial face
is selected. All faces in the mesh will be reordered to be consistent with that initial
face. The reordering is purely topological and has only to do with the order of ver-
tices, not with any geometric properties of the faces. As such, you get a consistent
ordering, but for a closed mesh, you might get all inward-pointing normals when in
9.3 Polymeshes, Polyhedra, and Polytopes 345
fact you wanted outward-pointing ones. If the desired ordering is known in advance,
additional information must be supplied to order the initial face as desired, perhaps
by some visibility test from an eye point. The initial face is marked as visited. If an
adjacent face has a consistent ordering with the initial face, then nothing is done to
the adjacent face. Otherwise, the ordering is inconsistent, and the adjacent triangle
is reordered to make it consistent. The adjacent triangle is then marked as visited,
and the search is applied recursively to its unvisited adjacent faces. The pseudocode
is listed below.
void MakeConsistent(Mesh mesh)
{
// assert: mesh is a connected manifold
// initially all faces are unvisited
Face f;
for (each face f in mesh)
f.visited = false;
// start the traversal at any face
Stack faceStack;
f = mesh.GetUnvisitedFace();
faceStack.Push(f);
f.visited = true;
// traverse the connected component of the starting triangle
while (not faceStack.empty()) {
// start at the current face
faceStack.Pop(f);
for(inti=0;i<f.numEdges; i++) {
// visit faces sharing an edge of f
Edge e = f.edge[i];
if (f has an adjacent face a to edge e) {
if (not a.visited) {
if (a.ContainsOrderedEdge(e.V(0), e.V(1))) {
// f and a have inconsistent orders
a.ReorderVertices();
}
faceStack.Push(a);
a.visited = true;
}
}
}
}
}
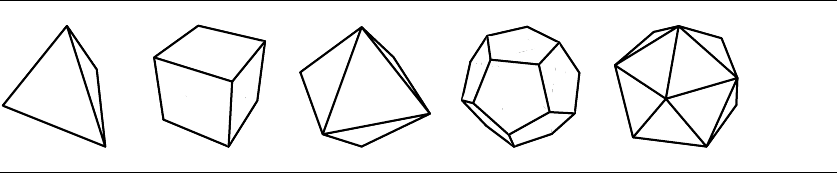
346 Chapter 9 Geometric Primitives in 3D
Figure 9.17 The five Platonic solids. Left to right: tetrahedron, hexahedron, octahedron, dodecahe-
dron, icosahedron.
9.3.6 Platonic Solids
A regular polygon is a convex polygon whose edge lengths are all the same and whose
angles between edges are all the same. For a specifed n ≥ 3, the vertices of a reg-
ular polygon inscribed in a unit circle are constructed by (x
k
, y
k
) = (cos(2πk/n),
sin(2πk/n)) for 0 ≤ k<n.Aregular polyhedron is a convex polyhedron whose faces
are congruent regular polygons and for which the number of faces sharing each ver-
tex is the same at each vertex. As it turns out, only five such polyhedra are possible,
but the proof is not given here. These polyhedra are called the Platonic solids.In
particular, the solids are a tetrahedron, a cube or hexahedron,anoctahedron,ado-
decahedron, and an icosahedron. Figure 9.17 illustrates the five solids. Provided here
are relationships between various quantities for a Platonic solid. A vertex-face table
can be constructed for each solid inscribed in the unit sphere; the tables are useful for
rendering the solids or for providing an initial polyhedron that is to be subdivided
for purposes of tessellating the sphere.
Let v, e, and f denote the number of vertices, edges, and faces, respectively, for
the solid. Euler’s formula relating these quantities is v −e + f = 2. Let p denote the
number of edges in a face, and let q denote the number of edges at each vertex. The
common edge length is denoted by L. The angle between two adjacent faces is called
a dihedral angle (literally di for “two” and hedra for “faces”) and is denoted A.The
radius of the circumscribed sphere is denoted by R, and the radius of the inscribed
sphere is denoted by r.ThesurfaceareaisdenotedbyS, and the volume is denoted
by V . All these quantites are interrelated by the equations
sin(A/2) = cos(π/q)/ sin(π/p) R/L = tan(π/q) tan(A/2)/2
r/L = cot(π/p) tan(A/2)/2 R/r =tan(π/p) tan(π/q)
S/L
2
= fp cot(π/p)/4 V = rS/3
Table 9.1 summarizes the relationships for the Platonic solids.
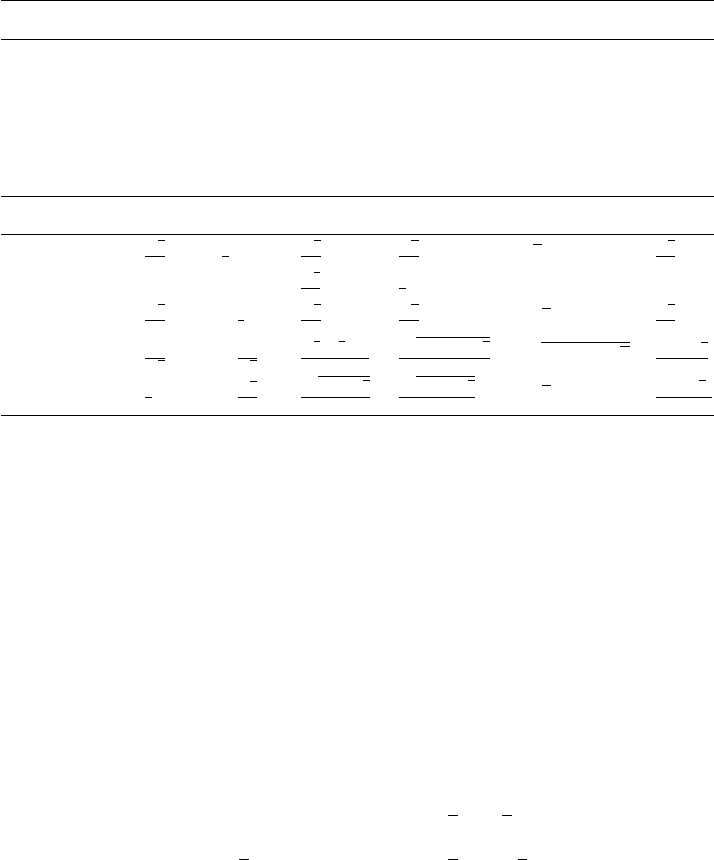
9.3 Polymeshes, Polyhedra, and Polytopes 347
Table 9.1
Various relationships for Platonic solids.
ve f p q
Tetrahedron 4 6 4 3 3
Hexahedron 8 12 6 4 3
Octahedron 6 12 8 3 4
Dodecahedron 20 30 12 5 3
Icosahedron 12 30 20 3 5
sin(A) cos(A) R/L r/L S/L
2
V /L
3
Tetrahedron
√
8
3
1
3
√
6
4
√
6
12
√
3
√
2
12
Hexahedron 1 0
√
3
2
1
2
61
Octahedron
√
8
3
−
1
3
√
2
2
√
6
6
2
√
3
√
2
3
Dodecahedron
2
√
5
−
1
√
5
√
3(
√
5+1)
4
√
250+110
√
5
20
3
25 + 10
√
5
15+7
√
5
4
Icosahedron
2
3
−
√
5
3
√
10+2
√
5
4
√
42+18
√
5
12
5
√
3
5(3+
√
5)
12
The following subsections provide vertex-face tables for the Platonic solids. The
polyhedron is centered at the origin and the vertices are all unit length. The face
connectivity is provided as a list of indices into the vertex array. The vertices of a face
are counterclockwise ordered as you look at the face from outside the polyhedron.
The faces for the tetrahedron, octahedron, and icosahedron are already triangles. The
faces for the hexahedron are squares, and the faces for the dodecahedron are pen-
tagons. In these two cases, a vertex-triangle table is also provided for those renderers
that support only triangle faces.
Tetrahedron
Theverticesare
V
0
= (0, 0, 1)V
2
= (−
√
2/3,
√
6/3, −1/3)
V
1
= (2
√
2/3, 0, −1/3)V
3
= (−
√
2/3, −
√
6/3, −1/3)
The triangle connectivity is
T
0
=0, 1, 2 T
2
=0, 3, 1
T
1
=0, 2, 3 T
3
=1, 3, 2

348 Chapter 9 Geometric Primitives in 3D
Hexahedron
Theverticesare
V
0
= (−1, −1, −1)/
√
3 V
4
= (−1, −1, 1)/
√
3
V
1
= (1, −1, −1)/
√
3 V
5
= (1, −1, 1)/
√
3
V
2
= (1, 1, −1)/
√
3 V
6
= (1, 1, 1)/
√
3
V
3
= (−1, 1, −1)/
√
3 V
7
= (−1, 1, 1)/
√
3
Thefaceconnectivityis
F
0
=0, 3, 2, 1 F
3
=6, 5, 1, 2
F
1
=0, 1, 5, 4 F
4
=6, 2, 3, 7
F
2
=0, 4, 7, 3 F
5
=6, 7, 4, 5
The triangle connectivity is
T
0
=0, 3, 2 T
6
=6, 5, 1
T
1
=0, 2, 1 T
7
=6, 1, 2
T
2
=0, 1, 5 T
8
=6, 2, 3
T
3
=0, 5, 4 T
9
=6, 3, 7
T
4
=0, 4, 7 T
10
=6, 7, 4
T
5
=0, 7, 3 T
11
=6, 4, 5
Octahedron
Theverticesare
V
0
= (1, 0, 0)V
3
= (0, −1, 0)
V
1
= (−1, 0, 0)V
4
= (0, 0, 1)
V
2
= (0, 1, 0)V
5
= (0, 0, −1)

9.3 Polymeshes, Polyhedra, and Polytopes 349
The triangle connectivity is
T
0
=4, 0, 2 T
4
=5, 2, 0
T
1
=4, 2, 1 T
5
=5, 1, 2
T
2
=4, 1, 3 T
6
=5, 3, 1
T
3
=4, 3, 0 T
7
=5, 0, 3
Dodecahedron
The vertices are constructed using the following intermediate terms: a = 1/
√
3, b =
(3 −
√
5)/6, and c =
(3 +
√
5)/6.Theverticesare
V
0
= (a, a, a) V
10
= (b, −c,0)
V
1
= (a, a, −a) V
11
= (−b, −c,0)
V
2
= (a, −a, a) V
12
= (c,0,b)
V
3
= (a, −a, −a) V
13
= (c,0,−b)
V
4
= (−a, a, a) V
14
= (−c,0,b)
V
5
= (−a, a, −a) V
15
= (−c,0,−b)
V
6
= (−a, −a, a) V
16
= (0, b, c)
V
7
= (−a, −a, −a) V
17
= (0, −b, c)
V
8
= (b, c,0)V
18
= (0, b, −c)
V
9
= (−b, c,0)V
19
= (0, −b, −c)
Thefaceconnectivityis
F
0
=0, 8, 9, 4, 16 F
6
=0, 12, 13, 1, 8
F
1
=0, 16, 17, 2, 12 F
7
=8, 1, 18, 5, 9
F
2
=12, 2, 10, 3, 13 F
8
=16, 4, 14, 6, 17
F
3
=9, 5, 15, 14, 4 F
9
=6, 11, 10, 2, 17
F
4
=3, 19, 18, 1, 13 F
10
=7, 15, 5, 18, 19
F
5
=7, 11, 6, 14, 15 F
11
=7, 19, 3, 10, 11
350 Chapter 9 Geometric Primitives in 3D
The triangle connectivity is
T
0
=0, 8, 9 T
12
=0, 9, 4 T
24
=0, 4, 16
T
1
=0, 12, 13 T
13
=0, 13, 1 T
25
=0, 1, 8
T
2
=0, 16, 17 T
14
=0, 17, 2 T
26
=0, 2, 12
T
3
=8, 1, 18 T
15
=8, 18, 5 T
27
=8, 5, 9
T
4
=12, 2, 10 T
16
=12, 10, 3 T
28
=12, 3, 13
T
5
=16, 4, 14 T
17
=16, 14, 6 T
29
=16, 6, 17
T
6
=9, 5, 15 T
18
=9, 15, 14 T
30
=9, 14, 4
T
7
=6, 11, 10 T
19
=6, 10, 2 T
31
=6, 2, 17
T
8
=3, 19, 18 T
20
=3, 18, 1 T
32
=3, 1, 13
T
9
=7, 15, 5 T
21
=7, 5, 18 T
33
=7, 18, 19
T
10
=7, 11, 6 T
22
=7, 6, 14 T
34
=7, 14, 15
T
11
=7, 19, 3 T
23
=7, 3, 10 T
35
=7, 10, 11
Icosahedron
Let t = (1 +
√
5)/2.Theverticesare
V
0
= (t,1,0)/
1 + t
2
V
6
= (−1, 0, t)/
1 + t
2
V
1
= (−t,1,0)/
1 + t
2
V
7
= (−1, 0, −t)/
1 + t
2
V
2
= (t, −1, 0)/
1 + t
2
V
8
= (0, t,1)/
1 + t
2
V
3
= (−t, −1, 0)/
1 + t
2
V
9
= (0, −t,1)/
1 + t
2
V
4
= (1, 0, t)/
1 + t
2
V
10
= (0, t, −1)/
1 + t
2
V
5
= (1, 0, −t)/
1 + t
2
V
11
= (0, −t, −1)/
1 + t
2

9.4 Quadric Surfaces 351
The triangle connectivity is
T
0
=0, 8, 4 T
10
=2, 9, 11
T
1
=0, 5, 10 T
11
=3, 11, 9
T
2
=2, 4, 9 T
12
=4, 2, 0
T
3
=2, 11, 5 T
13
=5, 0, 2
T
4
=1, 6, 8 T
14
=6, 1, 3
T
5
=1, 10, 7 T
15
=7, 3, 1
T
6
=3, 9, 6 T
16
=8, 6, 4
T
7
=3, 7, 11 T
17
=9, 4, 6
T
8
=0, 10, 8 T
18
=10, 5, 7
T
9
=1, 8, 10 T
19
=11, 7, 5
9.4 Quadric Surfaces
An excellent discussion of quadric surfaces is in Finney and Thomas (1996), but
considers all equations in axis-aligned form. The discussion here involves the general
quadratic equation and relies on an eigendecomposition of a matrix to characterize
the surfaces. The algorithm for eigendecomposition is discussed in Section A.3.
The general quadratic equation is X
T
AX + B
T
X + c = 0, where A isa3× 3
nonzero symmetric matrix, B isa3× 1 vector, and c is a scalar. The 3 × 1vec-
tor X represents the variable quantities. Since A is symmetric, it can be factored as
A = R
T
DR,whereD is a diagonal matrix whose diagonal entries are the eigenvalues
of A and R is a rotational matrix whose rows are corresponding eigenvectors. Setting
Y = RX and E = RB, the quadratic equation is Y
T
DY + E
T
Y + c = 0. The qua-
dratic equation can be factored by completing the square on terms. This allows us to
characterize the surface type or determine that the solution is degenerate (point, line,
plane). Let D =Diag(d
0
, d
1
, d
2
) and E = (e
0
, e
1
, e
2
).
9.4.1 Three Nonzero Eigenvalues
Thefactoredequationis
d
0
y
0
+
e
0
2d
0
2
+ d
1
y
1
+
e
1
2d
1
2
+ d
2
y
2
+
e
2
2d
2
2
+ c −
e
2
0
4d
0
−
e
2
1
4d
1
−
e
2
2
4d
2
= 0
Define γ
i
=−e
i
/(2d
i
) for i = 0, 1, 2, and define f = e
2
0
/4d
0
+ e
2
1
/4d
1
+ e
2
2
/4d
2
− c.
The equation is d
0
(y
0
− γ
0
)
2
+ d
1
(y
1
− γ
1
)
2
+ d
2
(y
2
− γ
2
)
2
= f .

352 Chapter 9 Geometric Primitives in 3D
Suppose f =0. If all eigenvalues are positive or all are negative, then the equation
represents a point (γ
0
, γ
1
, γ
2
). If at least one eigenvalue is positive and one eigenvalue
is negative, reorder terms and possibly multiply by −1 so that d
0
> 0, d
1
> 0, and
d
2
< 0. The equation is (y
2
− γ
2
)
2
= (−d
0
/d
2
)(y
0
− γ
0
)
2
+ (−d
1
/d
2
)(y
1
− γ
1
)
2
and
represents an elliptic cone (circular cone if d
0
= d
1
).
Suppose f>0; otherwise multiply the equation so that f is positive. If all eigen-
values are negative, then the equation has no solutions. If all the eigenvalues are
positive, the equation represents an ellipsoid. The center is (γ
0
, γ
1
, γ
2
) and the semi-
axis lengths are
f/d
i
for i = 0, 1, 2. If at least one eigenvalue is positive and one
eigenvalue is negative, then the equation represents a hyperboloid (one or two sheets
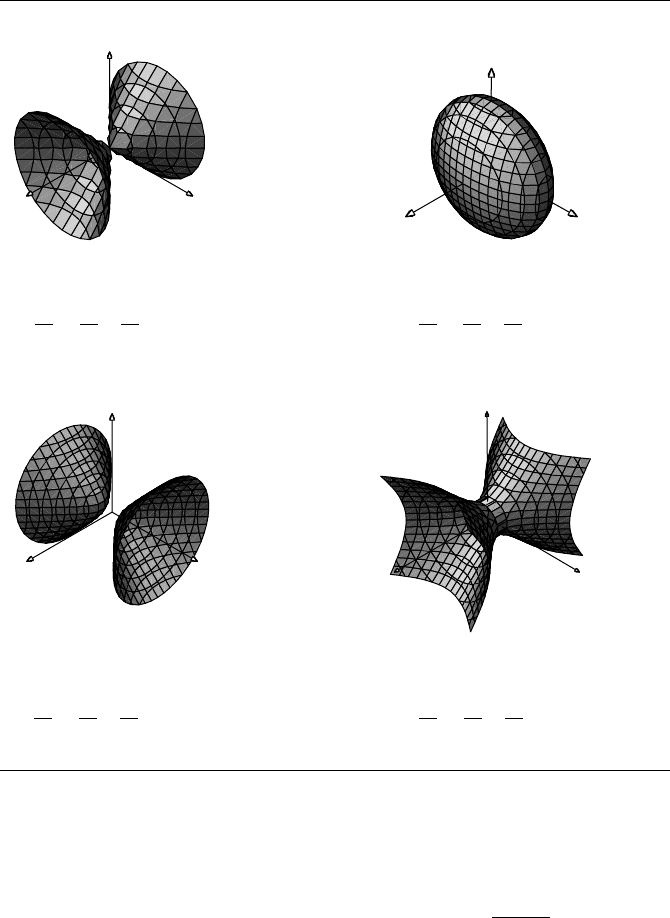
depending on number of positive eigenvalues). Figure 9.18 shows these quadrics,
along with their standard (axis-aligned) equations.
9.4.2 Two Nonzero Eigenvalues
Without loss of generality, assume that d
2
= 0.Thefactoredequationis
d
0
y
0
+
e
0
2d
0
2
+ d
1
y
1
+
e
1
2d
1
2
+ e
2
y
2
+ c −
e
2
0
4d
0
−
e
2
1
4d
1
= 0
Define γ
i
=−e
i
/(2d
i
) for i =0, 1, and define f =e
2
0
/4d
0
+e
2
1
/4d
1
−c. The equation
is d
0
(y
0
− γ
0
)
2
+ d
1
(y
1
− γ
1
)
2
+ e
2
y
2
= f .
Suppose e
2
= 0 and f = 0. If d
0
and d
1
are both positive or both negative, then
the equation represents a line containing (γ
0
, γ
1
,0) and having direction (0, 0, 1).
Otherwise the eigenvalues have opposite signs, and the equation represents the union
of two planes, y
1
− γ
1
=±
−d
0
/d
1
(y
0
− γ
0
).
Suppose e
2
= 0 and f>0 (if f<0, multiply the equation by −1). If d
0
and d
1
are both negative, then the equation has no solution. If both are positive, then the
equation represents an elliptic cylinder (a circular cylinder if d
0
= d
1
). Otherwise d
0
and d
1
have opposite signs, and the equation represents a hyperbolic cylinder.
Suppose e
2
=0. Define γ
2
=f/e
q
. The equation is d
0
(y
0
−γ
0
)
2
+d
1
(y
1
−γ
1
)
4
+
e
2
(y
2
− γ
2
) = 0. If d
0
and d
1
have the same sign, the equation represents an elliptic
paraboloid (circular paraboloid if d
0
= d
1
). Otherwise d
0
and d
1
have opposite signs,
and the equation represents a hyperbolic paraboloid. Figure 9.19 shows these quadrics.
9.4.3 One Nonzero Eigenvalue
Thefactoredequationis
d
0
y
0
+
e
0
2d
0
2
+ e
1
y
1
+ e
2
y
2
+ c −
e
2
0
4d
0
= 0
9.4 Quadric Surfaces 353
x
y
z
x
y
z
Ellipsoid
Hyperboloid of one sheet
x
2
a
2
y
2
b
2
z
2
c
2
+ +1=
x
2
a
2
y
2
b
2
z
2
c
2
+ –1=
x
y
z
x
y
z
Hyperboloid of two sheets
x
2
a
2
y
2
b
2
z
2
c
2
+ ––1=
Elliptic cone
x
2
a
2
y
2
b
2
z
2
c
2
+ –0=
Figure 9.18
Quadrics having three nonzero eigenvalues.
If e
1
= e
2
= 0, then the equation is degenerate (either no solution, or y
0
is constant,
in which case the solution is a plane). Otherwise, define L =
e
2
1
+ e
2
2
=0 and divide
the equation by L. Define α = d
0
/L, β = (c − e
2
0
/(4d
0
))/L, and make the rigid
change of variables z
0
= y
0
+ e
0
/(2d
0
), z
1
=−(e
1
y
1
+ e
2
y
2
)/L, and z
2
= (−e
2
y
1
+
e
1
y
2
)/L. The equation in the new coordinate system is z
1
= αz
2
0
+ β, so the surface
is a parabolic cylinder. Figure 9.20 shows these quadrics.
